15.3 : L'énergie dans un mouvement harmonique simple

Objectifs d'apprentissage

• Décrire la conservation de l'énergie du système composé d'une masse et d'un ressort
• Expliquer les concepts de points d'équilibre stables et instables

Pour produire une déformation dans un objet, il faut travailler. En d'autres termes, que vous tendiez une corde de guitare ou que vous compressiez l'amortisseur d'une voiture, une force doit être exercée à distance. Si le seul résultat est une déformation et qu'aucune œuvre n'est affectée à l'énergie thermique, sonore ou cinétique, alors tout le travail est initialement stocké dans l'objet déformé sous forme d'énergie potentielle.

Prenons l'exemple d'un bloc attaché à un ressort sur une table sans friction, oscillant en SHM. La force du ressort est une force conservatrice (que vous avez étudiée dans le chapitre sur l'énergie potentielle et la conservation de l'énergie), et nous pouvons définir une énergie potentielle pour celle-ci. Cette énergie potentielle est l'énergie stockée dans le ressort lorsque le ressort est étendu ou comprimé. Dans ce cas, le bloc oscille dans une dimension, la force du ressort agissant parallèlement au mouvement :

\[W = \int_{x_{i}}^{x_{f}} F_{x} dx \int_{x_{i}}^{x_{f}} -kxdx = \Big[ - \frac{1}{2} kx^{2} \Big]_{x_{i}}^{x_{f}} = - \Big[ \frac{1}{2} kx_{f}^{2} - \frac{1}{2} kx_{i}^{2} \Big] = - [U_{f} - U_{i}] = - \Delta U \ldotp\]

Si l'on considère l'énergie stockée dans un ressort, la position d'équilibre, marquée par x _i = 0,00 m, est la position à laquelle l'énergie stockée dans le ressort est égale à zéro. Lorsque le ressort est étiré ou comprimé sur une distance x, l'énergie potentielle stockée dans le ressort est

\[U = \frac{1}{2} kx^{2} \ldotp\]

L'énergie et l'oscillateur harmonique simple

Pour étudier l'énergie d'un oscillateur harmonique simple, nous devons prendre en compte toutes les formes d'énergie. Prenons l'exemple d'un bloc attaché à un ressort, placé sur une surface sans friction, oscillant en SHM. L'énergie potentielle stockée lors de la déformation du ressort est

\[U = \frac{1}{2} kx^{2} \ldotp\]

Dans un oscillateur harmonique simple, l'énergie oscille entre l'énergie cinétique de la masse K =\(\frac{1}{2}\) mv ² et l'énergie potentielle U =\(\frac{1}{2}\) kx ² stockée dans le ressort. Dans le SHM du système de masse et de ressort, il n'y a pas de forces dissipatives, de sorte que l'énergie totale est la somme de l'énergie potentielle et de l'énergie cinétique. Dans cette section, nous examinons la conservation de l'énergie du système. Les concepts examinés sont valables pour tous les oscillateurs harmoniques simples, y compris ceux où la force gravitationnelle joue un rôle.

Considérez la figure\(\PageIndex{1}\), qui montre un bloc oscillant attaché à un ressort. Dans le cas d'un SHM non amorti, l'énergie oscille entre la cinétique et le potentiel, passant complètement d'une forme d'énergie à l'autre au fur et à mesure que le système oscille. Ainsi, pour le simple exemple d'un objet sur une surface sans friction fixée à un ressort, le mouvement commence avec toute l'énergie stockée dans le ressort sous forme d'énergie potentielle élastique. Lorsque l'objet commence à bouger, l'énergie potentielle élastique est convertie en énergie cinétique, devenant entièrement de l'énergie cinétique à la position d'équilibre. L'énergie est ensuite reconvertie en énergie potentielle élastique par le ressort lorsqu'il est étiré ou comprimé. La vitesse devient nulle lorsque l'énergie cinétique est complètement convertie, et ce cycle se répète ensuite. Comprendre la conservation de l'énergie au cours de ces cycles fournira des informations supplémentaires ici et pour les applications ultérieures du SHM, telles que les circuits alternatifs.

Figure\(\PageIndex{1}\) : Transformation de l'énergie en SHM pour un objet fixé à un ressort sur une surface sans friction. (a) Lorsque la masse est à la position x = + A, toute l'énergie est stockée sous forme d'énergie potentielle dans le ressort U =\(\frac{1}{2}\) kA ². L'énergie cinétique est égale à zéro car la vitesse de la masse est nulle. (b) Lorsque la masse se déplace vers x = −A, elle franchit la position x = 0. À ce stade, le ressort n'est ni étendu ni comprimé, de sorte que l'énergie potentielle stockée dans le ressort est nulle. À x = 0, l'énergie totale est toute l'énergie cinétique où K =\(\frac{1}{2}\) m (−v _max) ². (c) La masse continue de se déplacer jusqu'à ce qu'elle atteigne x = −A où elle s'arrête et commence à se déplacer vers x = + A. À la position x = −A, l'énergie totale est stockée sous forme d'énergie potentielle dans le U =\(\frac{1}{2}\) k (−A) ² comprimé et l'énergie cinétique est nulle. (d) Lorsque la masse passe par la position x = 0, l'énergie cinétique est K =\(\frac{1}{2}\) mv _max ² et l'énergie potentielle stockée dans le ressort est nulle. (e) La masse revient à la position x = + A, où K = 0 et U =\(\frac{1}{2}\) kA ².

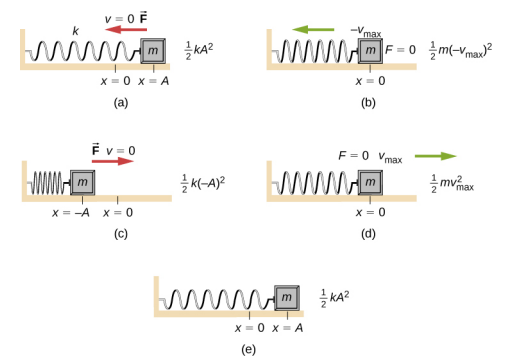
Considérez la figure\(\PageIndex{1}\), qui montre l'énergie à des points spécifiques du mouvement périodique. Tout en restant constante, l'énergie oscille entre l'énergie cinétique du bloc et l'énergie potentielle stockée dans le ressort :

\[E_{Total} = U + K = \frac{1}{2} kx^{2} + \frac{1}{2} mv^{2} \ldotp\]

Le mouvement du bloc sur un ressort dans SHM est défini par la position x (t) = Acos (\(\omega\)t+\(\phi\)) avec une vitesse de v (t) = −A\(\omega\) sin (\(\omega\)t +\(\phi\)). À l'aide de ces équations, l'identité trigonométrique cos ^{2\(\theta\) + sin 2}\(\theta\) = 1 et\(\omega = \sqrt{\frac{k}{m}}\), nous pouvons trouver l'énergie totale du système :

\[\begin{split} E_{Total} & = \frac{1}{2} kA^{2} \cos^{2} (\omega t + \phi) + \frac{1}{2} mA^{2} \omega^{2} \sin^{2} (\omega t + \phi) \\ & = \frac{1}{2} kA^{2} \cos^{2} (\omega t + \phi) + \frac{1}{2} mA^{2} \left(\dfrac{k}{m}\right) \sin^{2} (\omega t + \phi) \\ & = \frac{1}{2} kA^{2} \cos^{2} (\omega t + \phi) + \frac{1}{2} kA^{2} \sin^{2} (\omega t + \phi) \\ & = \frac{1}{2} kA^{2} \cos^{2} (\omega t + \phi) + \frac{1}{2} mA^{2} \omega^{2} \sin^{2} (\omega t + \phi) \\ & = \frac{1}{2} kA^{2} (\cos^{2} (\omega t + \phi) + \sin^{2} (\omega t + \phi)) \\ & = \frac{1}{2} kA^{2} \ldotp \end{split}\]

L'énergie totale du système composé d'un bloc et d'un ressort est égale à la somme de l'énergie potentielle stockée dans le ressort plus l'énergie cinétique du bloc et est proportionnelle au carré de l'amplitude E _Total =\(\left(\dfrac{1}{2}\right)\) kA ². L'énergie totale du système est constante.

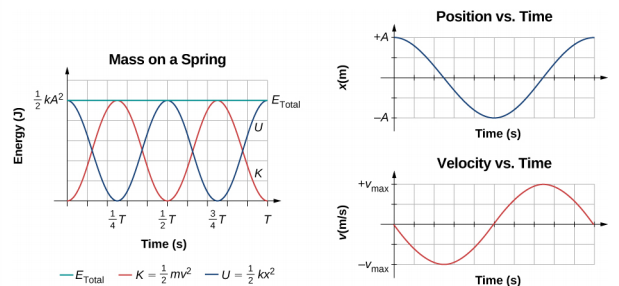
Un examen plus approfondi de l'énergie du système montre que l'énergie cinétique oscille comme une fonction sinusoïdale au carré, tandis que l'énergie potentielle oscille comme une fonction cosinusoïdale au carré. Cependant, l'énergie totale du système est constante et proportionnelle à l'amplitude au carré. La figure\(\PageIndex{2}\) montre un graphique des énergies potentielle, cinétique et totale du système de blocs et de ressorts en fonction du temps. La position et la vitesse en fonction du temps sont également tracées. Avant le temps t = 0,0 s, le bloc est attaché au ressort et placé en position d'équilibre. Le travail est effectué sur le bloc en appliquant une force externe, en le tirant jusqu'à une position de x = + A. Le système possède désormais de l'énergie potentielle stockée dans le ressort. Au temps t = 0,00 s, la position du bloc est égale à l'amplitude, l'énergie potentielle stockée dans le ressort est égale à U =\(\frac{1}{2}\) kA ² et la force sur le bloc est maximale et pointe dans la direction X négative (F _S = −kA). La vitesse et l'énergie cinétique du bloc sont nulles au temps t = 0,00 s. Au temps t = 0,00 s, le bloc est libéré du repos.

Figure\(\PageIndex{2}\) : Graphique de l'énergie cinétique, de l'énergie potentielle et de l'énergie totale d'un bloc oscillant sur un ressort dans SHM. Les graphiques de la position en fonction du temps et de la vitesse en fonction du temps sont également présentés. L'énergie totale reste constante, mais l'énergie oscille entre l'énergie cinétique et l'énergie potentielle. Lorsque l'énergie cinétique est maximale, l'énergie potentielle est nulle. Cela se produit lorsque la vitesse est maximale et que la masse est en position d'équilibre. L'énergie potentielle est maximale lorsque la vitesse est nulle. L'énergie totale est la somme de l'énergie cinétique et de l'énergie potentielle et elle est constante.

Oscillations relatives à une position d'équilibre

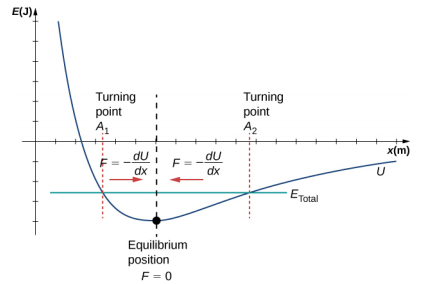
Nous venons de considérer l'énergie du SHM en fonction du temps. Un autre point de vue intéressant de l'oscillateur harmonique simple consiste à considérer l'énergie en fonction de la position. La figure\(\PageIndex{3}\) montre un graphique de l'énergie en fonction de la position d'un système soumis à une SHM.

Figure\(\PageIndex{3}\) : graphique de l'énergie cinétique (rouge), de l'énergie potentielle (bleu) et de l'énergie totale (vert) d'un oscillateur harmonique simple. La force est égale à F = −\(\frac{dU}{dx}\). La position d'équilibre est indiquée par un point noir et correspond au point où la force est égale à zéro. La force est positive lorsque x < 0, negative when x > 0 et égale à zéro lorsque x = 0.

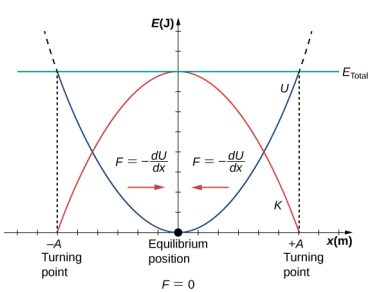
La courbe d'énergie potentielle de la figure\(\PageIndex{3}\) ressemble à un bol. Lorsqu'une bille est placée dans un bol, elle retrouve la position d'équilibre au point le plus bas du bol (x = 0). Cela se produit parce qu'une force de rappel pointe vers le point d'équilibre. Ce point d'équilibre est parfois appelé point fixe. Lorsque la bille est déplacée vers une position différente (x = + A), elle oscille autour de la position d'équilibre. Si l'on regarde le graphique de l'énergie potentielle, la force peut être déterminée en examinant la pente du graphe de l'énergie potentielle (F = −\(\frac{dU}{dx}\)). Puisque la force de chaque côté du point fixe pointe vers le point d'équilibre, le point d'équilibre est appelé point d'équilibre stable. Les points x = A et x = −A sont appelés points de retournement. (Voir Énergie potentielle et économies d'énergie.) La stabilité est un concept important. Si un point d'équilibre est stable, une légère perturbation d'un objet qui se trouve initialement au point d'équilibre stable fera osciller l'objet autour de ce point. Le point d'équilibre stable se produit parce que la force de chaque côté est dirigée vers lui. Pour un point d'équilibre instable, si l'objet est légèrement perturbé, il ne revient pas au point d'équilibre.

Prenons l'exemple du marbre dans le bol. Si le bol est placé du côté droit vers le haut, la bille, si elle est légèrement perturbée, oscillera autour du point d'équilibre stable. Si le bol est retourné, la bille peut être équilibrée sur le dessus, au point d'équilibre où la force nette est nulle. Cependant, si la bille est légèrement perturbée, elle ne reviendra pas au point d'équilibre, mais tombera du bol. La raison en est que la force de chaque côté du point d'équilibre est dirigée à l'opposé de ce point. Ce point est un point d'équilibre instable.

La figure\(\PageIndex{4}\) montre trois conditions. Le premier est un point d'équilibre stable (a), le second est un point d'équilibre instable (b) et le dernier est également un point d'équilibre instable (c), car la force d'un seul côté pointe vers le point d'équilibre.

Figure\(\PageIndex{4}\) : Exemples de points d'équilibre. (a) Point d'équilibre stable ; (b) point d'équilibre instable ; (c) point d'équilibre instable (parfois appelé point d'équilibre semi-stable).

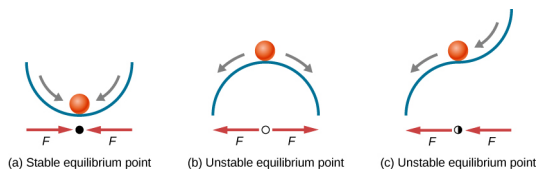
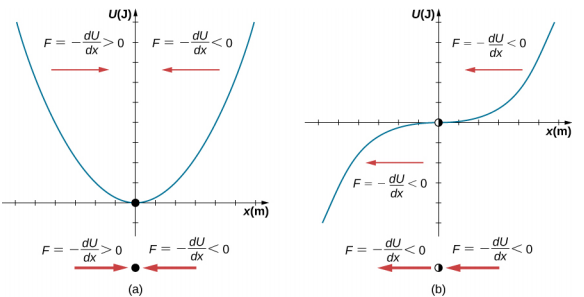
Le processus permettant de déterminer si un point d'équilibre est stable ou instable peut être formalisé. Considérez les courbes d'énergie potentielle présentées sur la figure\(\PageIndex{5}\). La force peut être déterminée en analysant la pente du graphique. La force est F = −\(\frac{dU}{dx}\). Dans (a), le point fixe est à x = 0,00 m. Lorsque x < 0,00 m, la force est positive. Lorsque x est supérieur à 0,00 m, la force est négative. Il s'agit d'un point stable. Dans (b), le point fixe est à x = 0,00 m. Lorsque x < 0,00 m, la force est négative. Lorsque x est supérieur à 0,00 m, la force est également négative. Il s'agit d'un point instable.

Figure\(\PageIndex{5}\) : Deux exemples de fonction énergétique potentielle. La force appliquée à une position est égale à la valeur négative de la pente du graphe à cette position. (a) Une fonction énergétique potentielle avec un point d'équilibre stable. (b) Une fonction énergétique potentielle avec un point d'équilibre instable. Ce point est parfois appelé semi-stable parce que la force exercée sur un côté pointe vers le point fixe.

Une application pratique du concept de points d'équilibre stables est la force entre deux atomes neutres dans une molécule. Si deux molécules se trouvent à proximité, séparées par quelques diamètres atomiques, elles peuvent ressentir une force d'attraction. Si les molécules se rapprochent suffisamment pour que les couches électroniques des autres électrons se chevauchent, la force entre les molécules devient répulsive. La force d'attraction entre les deux atomes peut amener les atomes à former une molécule. La force entre les deux molécules n'est pas une force linéaire et ne peut pas être modélisée simplement comme deux masses séparées par un ressort, mais les atomes de la molécule peuvent osciller autour d'un point d'équilibre lorsqu'ils sont légèrement déplacés par rapport à la position d'équilibre. Les atomes oscillent en raison de la force d'attraction et de la force répulsive entre les deux atomes.

Prenons un exemple d'interaction entre deux atomes connue sous le nom d'interaction de Van Der Waals. Il n'entre pas dans le cadre de ce chapitre de discuter en profondeur des interactions entre les deux atomes, mais les oscillations des atomes peuvent être examinées en considérant un exemple de modèle de l'énergie potentielle du système. Une suggestion pour modéliser l'énergie potentielle de cette molécule est d'utiliser le potentiel 6-12 de Lennard-Jones :

\[U(x) = 4 \epsilon \Bigg[ \left(\dfrac{\sigma}{x}\right)^{12} - \left(\dfrac{\sigma}{x}\right)^{6} \Bigg] \ldotp\]

Un graphique de cette fonction est illustré à la figure\(\PageIndex{6}\). Les deux paramètres\(\epsilon\) et\(\sigma\) sont trouvés expérimentalement.

Figure\(\PageIndex{6}\) : La fonction énergétique potentielle de Lennard-Jones pour un système de deux atomes neutres. Si l'énergie est inférieure à une certaine énergie maximale, le système oscille à proximité de la position d'équilibre entre les deux points de retournement.

Sur le graphique, vous pouvez voir qu'il existe un puits d'énergie potentiel, qui présente certaines similitudes avec le puits d'énergie potentielle de la fonction d'énergie potentielle de l'oscillateur harmonique simple décrit dans la figure\(\PageIndex{3}\). Le potentiel de Lennard-Jones possède un point d'équilibre stable où l'énergie potentielle est minimale et où la force de chaque côté du point d'équilibre pointe vers le point d'équilibre. Notez que contrairement à l'oscillateur harmonique simple, le puits de potentiel du potentiel de Lennard-Jones n'est pas symétrique. Cela est dû au fait que la force entre les atomes n'est pas une force légale de Hooke et n'est pas linéaire. Les atomes peuvent toujours osciller autour de la position d'équilibre x _min car lorsque x < x _min, la force est positive ; lorsque x > x _min, la force est négative. Notez que lorsque x approche de zéro, la pente est assez raide et négative, ce qui signifie que la force est importante et positive. Cela suggère qu'il faut une force importante pour essayer de rapprocher les atomes. À mesure que x devient de plus en plus grand, la pente devient moins raide et la force est plus faible et négative. Cela suggère que si l'on leur donne une énergie suffisante, les atomes peuvent être séparés.

Si cette interaction vous intéresse, déterminez la force entre les molécules en prenant la dérivée de la fonction énergétique potentielle. Vous verrez immédiatement que la force ne ressemble pas à une force de loi de Hooke (F = −kx), mais si vous connaissez le théorème binomial :

\[(1 + x)^{n} = 1 + nx + \frac{n(n - 1)}{2!} x^{2} + \frac{n(n - 1)(n - 2)}{3!} x^{3} + \cdots,\]

la force peut être approximée par une force de police de Hooke.

Vitesse et conservation de l'énergie

Pour en revenir au système d'un bloc et d'un ressort de la figure\(\PageIndex{1}\), une fois que le bloc est libéré du repos, il commence à se déplacer dans la direction négative vers la position d'équilibre. L'énergie potentielle diminue et l'amplitude de la vitesse et de l'énergie cinétique augmentent. Au temps t =\(\frac{T}{4}\), le bloc atteint la position d'équilibre x = 0,00 m, où la force exercée sur le bloc et l'énergie potentielle sont nulles. À la position d'équilibre, le bloc atteint une vitesse négative d'une amplitude égale à la vitesse maximale v = −A\(\omega\). L'énergie cinétique est maximale et égale à K =\(\frac{1}{2}\) mv ² =\(\frac{1}{2}\) mA ² ω\(\omega^{2}\) =\(\frac{1}{2}\) kA ². À ce stade, la force exercée sur le bloc est nulle, mais le moment transporte le bloc, et il continue dans la direction négative vers x = −A. Lorsque le bloc continue de se déplacer, la force exercée sur celui-ci agit dans le sens positif et l'amplitude de la vitesse et de l'énergie cinétique diminuent. L'énergie potentielle augmente à mesure que le ressort se comprime. Au temps t =\(\frac{T}{2}\), le bloc atteint x = −A. Ici, la vitesse et l'énergie cinétique sont égales à zéro. La force exercée sur le bloc est F = + kA et l'énergie potentielle stockée dans le ressort est U =\(\frac{1}{2}\) kA ². Pendant les oscillations, l'énergie totale est constante et égale à la somme de l'énergie potentielle et de l'énergie cinétique du système,

\[E_{Total} = \frac{1}{2} kx^{2} + \frac{1}{2} mv^{2} = \frac{1}{2} kA^{2} \ldotp \label{15.12}\]

L'équation de l'énergie associée au SHM peut être résolue pour déterminer l'amplitude de la vitesse à n'importe quelle position :

\[|v| = \sqrt{\frac{k}{m} (A^{2} - x^{2})} \ldotp \label{15.13}\]

L'énergie d'un oscillateur harmonique simple est proportionnelle au carré de l'amplitude. Lorsque vous considérez de nombreuses formes d'oscillations, vous trouverez l'énergie proportionnelle à l'amplitude au carré.

Exercice 15.1

Pourquoi serait-il plus douloureux de claquer votre main avec une règle qu'avec un ressort lâche, même si le déplacement de chaque système est égal ?

Exercice 15.2

Identifiez un moyen de réduire la vitesse maximale d'un oscillateur harmonique simple.