14.8 : Équation de Bernoulli

Objectifs d'apprentissage

• Expliquez les termes de l'équation de Bernoulli
• Expliquer comment l'équation de Bernoulli est liée à la conservation de l'énergie
• Décrire comment dériver le principe de Bernoulli à partir de l'équation de Bernoulli
• Effectuer des calculs en utilisant le principe de Bernoulli
• Décrivez certaines applications du principe de Bernoulli

Comme nous l'avons montré à la Figure 14.7.4, lorsqu'un fluide s'écoule dans un canal plus étroit, sa vitesse augmente. Cela signifie que son énergie cinétique augmente également. L'énergie cinétique accrue provient du réseau effectué sur le fluide pour le pousser dans le canal. De plus, si le fluide change de position verticale, un travail est effectué sur le fluide par la force gravitationnelle.

Une différence de pression se produit lorsque le canal se rétrécit. Cette différence de pression se traduit par une force nette sur le fluide, car la pression multipliée par la surface est égale à la force, et cette force nette fonctionne. Rappelons le théorème travail-énergie,

\[W_{net} = \frac{1}{2} mv^{2} - \frac{1}{2} mv_{0}^{2} \ldotp\]

Le réseau effectué augmente l'énergie cinétique du fluide. Par conséquent, la pression chute dans un fluide en mouvement rapide, que le fluide soit confiné ou non dans un tube.

Il existe de nombreux exemples courants de chute de pression dans des fluides en mouvement rapide. Par exemple, les rideaux de douche ont la fâcheuse habitude de s'enfoncer dans la cabine de douche lorsque celle-ci est allumée. La raison en est que le flux d'eau et d'air à haute vitesse crée une zone de pression plus faible à l'intérieur de la douche, alors que la pression de l'autre côté reste à la pression atmosphérique normale. Cette différence de pression se traduit par une force nette qui pousse le rideau vers l'intérieur. De même, lorsqu'une voiture croise un camion sur l'autoroute, les deux véhicules semblent se tirer l'un vers l'autre. La raison est la même : la vitesse élevée de l'air entre la voiture et le camion crée une zone de pression plus faible entre les véhicules, qui sont poussés l'un contre l'autre par une pression extérieure plus importante (Figure\(\PageIndex{1}\)). Cet effet a été observé dès le milieu des années 1800, lorsqu'on a découvert que les trains circulant dans des directions opposées basculaient de façon précaire l'un vers l'autre.

Figure\(\PageIndex{1}\) : Vue aérienne d'une voiture passant devant un camion sur une autoroute. L'air passant entre les véhicules s'écoule dans un canal plus étroit et doit augmenter sa vitesse (v2 est supérieure à v1), provoquant une baisse de pression entre les véhicules (pi est inférieur à po). Une pression extérieure accrue permet de rapprocher la voiture et le camion.

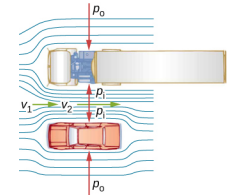
Conservation de l'énergie et équation de Bernoulli

L'application du principe de conservation de l'énergie à un écoulement laminaire sans friction permet d'établir une relation très utile entre la pression et la vitesse d'écoulement dans un fluide. Cette relation est appelée équation de Bernoulli, du nom de Daniel Bernoulli (1700—1782), qui a publié ses études sur le mouvement des fluides dans son livre Hydrodynamica (1738).

Prenons l'exemple d'un fluide incompressible s'écoulant dans un tuyau dont le diamètre et la hauteur varient, comme le montre la figure\(\PageIndex{2}\). Les indices 1 et 2 de la figure indiquent deux emplacements le long du tuyau et illustrent les relations entre les surfaces des sections transversales A, la vitesse d'écoulement v, la hauteur par rapport au sol y et la pression p en chaque point. Nous supposons ici que la densité aux deux points est la même (par conséquent, la densité est indiquée\(\rho\) sans indice) et que, comme le fluide est incompressible, les volumes ombrés doivent être égaux.

Figure\(\PageIndex{2}\) : La géométrie utilisée pour la dérivation de l'équation de Bernoulli.

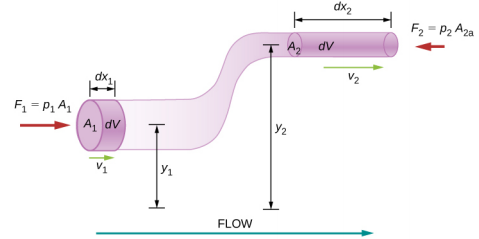
Nous supposons également qu'il n'y a aucune force visqueuse dans le fluide, de sorte que l'énergie de n'importe quelle partie du fluide sera conservée. Pour dériver l'équation de Bernoulli, nous calculons d'abord le travail qui a été effectué sur le fluide :

\[\begin{split} dW & = F_{1} dx_{1} - F_{2} dx_{2} \\ & = p_{1} A_{1} dx_{1} - p_{2} A_{2} dx_{2} \\ & = p_{1} dV - p_{2} dV = (p_{1} - p_{2}) dV \ldotp \end{split}\]

Le travail effectué était dû à la force de gravité conservatrice et à la modification de l'énergie cinétique du fluide. La variation de l'énergie cinétique du fluide est égale à

\[dK = \frac{1}{2} m_{2} v_{2}^{2} - \frac{1}{2} m_{1} v_{1}^{2} = \frac{1}{2} \rho dV (v_{2}^{2} - v_{1}^{2}) \ldotp\]

Le changement d'énergie potentielle est

\[dU = mgy_{2} - mgy_{1} = \rho dV g(y_{2} - y_{1}) \ldotp\]

L'équation énergétique devient alors

\[\begin{split} dW & = dK + dU \\ (p_{1} - p_{2}) dV & = \frac{1}{2} \rho dV (v_{2}^{2} - v_{1}^{2}) + \rho dV g(y_{2} - y_{1}) \\ (p_{1} - p_{2}) & = \frac{1}{2} \rho (v_{2}^{2} - v_{1}^{2}) + \rho g(y_{2} - y_{1}) \ldotp \end{split}\]

La réorganisation de l'équation donne l'équation de Bernoulli :

\[p_{1} + \frac{1}{2} \rho v_{1}^{2} + \rho gy_{1} = p_{2} + \frac{1}{2} \rho v_{2}^{2} + \rho gy_{2} \ldotp\]

Cette relation indique que l'énergie mécanique de n'importe quelle partie du fluide change en raison du travail effectué par le fluide à l'extérieur de cette partie, en raison de la pression variable en cours de route. Les deux points ayant été choisis de manière arbitraire, nous pouvons écrire l'équation de Bernoulli de manière plus générale en tant que principe de conservation le long du flux.

Équation de Bernoulli

Pour un fluide incompressible et sans friction, la combinaison de la pression et de la somme des densités d'énergie cinétique et potentielle est constante non seulement dans le temps, mais également le long d'une ligne droite :

\[p + \frac{1}{2} \rho v^{2} + \rho gy = constant \label{14.16}\]

Il convient de noter en particulier que, dans une situation dynamique, les pressions à la même hauteur dans différentes parties du fluide peuvent être différentes si elles ont des vitesses d'écoulement différentes.

Analyse de l'équation de Bernoulli

Selon l'équation de Bernoulli, si nous suivons un petit volume de fluide le long de son trajet, différentes quantités de la somme peuvent changer, mais le total reste constant. L'équation de Bernoulli n'est en fait qu'une déclaration pratique de conservation de l'énergie pour un fluide incompressible en l'absence de friction.

La forme générale de l'équation de Bernoulli comporte trois termes et elle est largement applicable. Pour mieux le comprendre, examinons quelques situations spécifiques qui simplifient et illustrent son utilisation et sa signification.

Équation de Bernoulli pour les fluides statiques

Considérez d'abord la situation très simple où le fluide est statique, c'est-à-dire\(v_1 = v_2 = 0\). L'équation de Bernoulli dans ce cas est

\[p_{1} + \rho gh_{1} = p_{2} + \rho gh_{2} \ldotp\]

Nous pouvons simplifier davantage l'équation en définissant h ₂ = 0. (N'importe quelle hauteur peut être choisie pour une hauteur de référence nulle, comme c'est souvent le cas pour d'autres situations impliquant une force gravitationnelle, toutes les autres hauteurs étant relatives.) Dans ce cas, nous obtenons

\[p_{2} = p_{1} + \rho gh_{1} \ldotp\]

Cette équation nous indique que, dans les fluides statiques, la pression augmente avec la profondeur. Lorsque l'on passe d'un point 1 à un point 2 dans le fluide, la profondeur augmente de h ₁, et par conséquent, p ₂ est supérieur à p ₁ d'une certaine quantité\(\rho gh_1\). Dans le cas le plus simple, p ₁ est zéro au sommet du fluide, et nous obtenons la relation familière\(p = \rho gh\). (Rappelez-vous que p =\(\rho gh\) et\(\Delta Ug = −mgh\).) Ainsi, l'équation de Bernoulli confirme le fait que le changement de pression dû au poids d'un fluide est\(\rho gh\). Bien que nous introduisions l'équation de Bernoulli pour le mouvement des fluides, elle inclut une grande partie de ce que nous avons étudié précédemment pour les fluides statiques.

Le principe de Bernoulli

Supposons qu'un fluide se déplace mais que sa profondeur soit constante, c'est-à-dire\(h_1 = h_2\). Dans ces conditions, l'équation de Bernoulli devient

\[p_{1} + \frac{1}{2} \rho v_{1}^{2} = p_{2} + \frac{1}{2} \rho v_{2}^{2} \ldotp \label{Bernoulli}\]

Les situations dans lesquelles un fluide s'écoule à une profondeur constante sont si courantes que cette équation est souvent appelée principe de Bernoulli, qui est simplement l'équation de Bernoulli pour les fluides à profondeur constante. (Notez à nouveau que cela s'applique à un petit volume de liquide lorsque nous le suivons sur sa trajectoire.) Le principe de Bernoulli renforce le fait que la pression chute à mesure que la vitesse augmente dans un fluide en mouvement : si v ₂ est supérieur à v ₁ dans l'équation, alors p ₂ doit être inférieur à p ₁ pour que l'égalité soit maintenue.

Exemple 14.6 : Calcul de la pression

Dans l'exemple 14.5, nous avons constaté que la vitesse de l'eau dans un tuyau augmentait de 1,96 m/s à 25,5 m/s entre le tuyau et la buse. Calculez la pression dans le tuyau, étant donné que la pression absolue dans la buse est de 1,01 x 10 ⁵ N/m ² (atmosphérique, comme il se doit) et en supposant un débit uniforme et sans friction.

Stratégie

Le débit horizontal signifie une profondeur constante, c'est pourquoi le principe de Bernoulli s'applique. Nous utilisons l'indice 1 pour les valeurs dans le tuyau et 2 pour celles dans la buse. On nous demande donc de trouver p ₁.

Solution

Résoudre le principe de Bernoulli (équation de Bernoulli) pour les\(p_1\) rendements

\[ \begin{align*} p_{1} &= p_{2} \frac{1}{2} \rho v_{2}^{2} - \frac{1}{2} \rho v_{1}^{2} \\[4pt] &= p_{2} + \frac{1}{2} \rho (v_{2}^{2} - v_{1}^{2}) \ldotp \end{align*}\]

En substituant des valeurs connues,

\[\begin{align*} p_{1} & = (1.01 \times 10^{5}\; N/m^{2}) + \frac{1}{2} (10^{3}\; kg/m^{3})[(25.5\; m/s)^{2} - (1.96\; m/s)^{2}] \\[4pt] & = 4.24 \times 10^{5}\; N/m^{2} \ldotp \end{align*}\]

L'importance

Cette pression absolue dans le tuyau est supérieure à celle dans la buse, comme prévu, puisque v est plus élevé dans la buse. La pression p ₂ dans la buse doit être atmosphérique, car l'eau émerge dans l'atmosphère sans autre changement de conditions.

Applications du principe de Bernoulli

De nombreux appareils et situations se produisent dans lesquels le fluide s'écoule à une hauteur constante et peuvent donc être analysés selon le principe de Bernoulli.

Entraînement

Les gens appliquent depuis longtemps le principe de Bernoulli en utilisant la pression réduite dans des fluides à haute vitesse pour déplacer des objets. Lorsque la pression extérieure est plus élevée, le fluide à grande vitesse force d'autres fluides à pénétrer dans le flux. Ce processus s'appelle l'entraînement. Les dispositifs d'entraînement sont utilisés depuis l'Antiquité comme pompes pour élever l'eau à de petites hauteurs, comme cela est nécessaire pour drainer les marécages, les champs ou d'autres zones basses. Certains autres appareils utilisant le concept d'entraînement sont illustrés sur la figure\(\PageIndex{3}\).

Figure\(\PageIndex{3}\) : Les dispositifs d'entraînement utilisent la vitesse accrue du fluide pour créer de basses pressions, qui entraînent ensuite un fluide dans un autre. a) Un brûleur Bunsen utilise une buse à gaz réglable qui entraîne l'air pour une combustion correcte. (b) Un atomiseur utilise une ampoule à pression pour créer un jet d'air qui entraîne les gouttes de parfum. Les pulvérisateurs de peinture et les carburateurs utilisent des techniques très similaires pour déplacer leurs liquides respectifs. (c) Un aspirateur ordinaire utilise un jet d'eau à grande vitesse pour créer une zone de pression plus basse. Les aspirateurs peuvent être utilisés comme pompes d'aspiration dans des situations dentaires et chirurgicales, pour drainer un sous-sol inondé ou pour réduire la pression dans un vaisseau. d) La cheminée d'un chauffe-eau est conçue pour entraîner l'air dans le tuyau traversant le plafond.

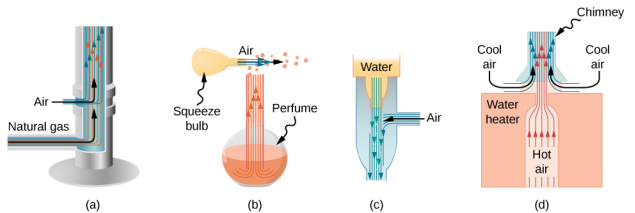
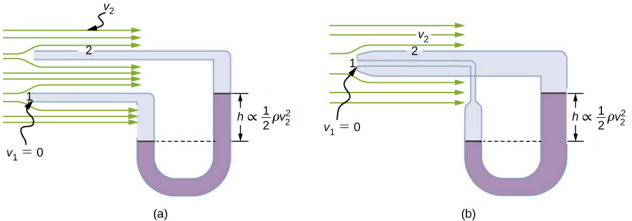
Mesure de la vitesse

La figure\(\PageIndex{4}\) montre deux appareils qui appliquent le principe de Bernoulli pour mesurer la vitesse d'un fluide. La partie (a) du manomètre est connectée à deux tubes suffisamment petits pour ne pas perturber sensiblement le débit. Le tube faisant face au fluide venant en sens inverse crée un point mort à vitesse nulle (v ₁ = 0) devant lui, tandis que le fluide passant par l'autre tube a une vitesse v ₂. Cela signifie que le principe de Bernoulli tel qu'énoncé dans

\[p_{1} + \frac{1}{2} \rho v_{1}^{2} = p_{2} + \frac{1}{2} \rho v_{2}^{2}\]

devient

\[p_{1} = p_{2} + \frac{1}{2} \rho v_{2}^{2} \ldotp\]

Ainsi, la pression p ₂ au-dessus de la deuxième ouverture est réduite de\(\frac{1}{2} \rho v_{2}^{2}\), de sorte que le fluide dans le manomètre augmente de h du côté connecté à la seconde ouverture, où

\[h \propto \frac{1}{2} \rho v_{2}^{2} \ldotp\]

(Rappelez-vous que le symbole\(\propto\) signifie « proportionnel à ».) En résolvant la _{version 2}, nous voyons que

\[v_{2} \propto \sqrt{h} \ldotp\]

La partie (b) montre une version de cet appareil couramment utilisée pour mesurer diverses vitesses de fluide ; de tels dispositifs sont fréquemment utilisés comme indicateurs de vitesse dans les aéronefs.

Figure\(\PageIndex{4}\) : Mesure de la vitesse du fluide selon le principe de Bernoulli. a) Un manomètre est raccordé à deux tubes rapprochés et suffisamment petits pour ne pas perturber le débit. Le tube 1 est ouvert à l'extrémité faisant face au flux. Un point mort à vitesse nulle y est créé. Le tube 2 possède une ouverture latérale, de sorte que le fluide a une vitesse v à travers l'ouverture ; ainsi, la pression y chute. La différence de pression au manomètre est de\(\frac{1}{2} \rho v_{2}^{2}\), donc h est proportionnel à\(\frac{1}{2} \rho v_{2}^{2}\). (b) Ce type d'appareil de mesure de la vitesse est un tube de Prandtl, également connu sous le nom de tube de Pitot.

Une lance à incendie

Toutes les applications précédentes de l'équation de Bernoulli impliquaient de simplifier les conditions, telles que la hauteur constante ou la pression constante. L'exemple suivant est une application plus générale de l'équation de Bernoulli dans laquelle la pression, la vitesse et la hauteur changent toutes.

Exemple 14.7 : Calcul de la pression - Une buse d'incendie

Les tuyaux d'incendie utilisés lors de grands incendies structurels ont un diamètre intérieur de 6,40 cm (Figure\(\PageIndex{5}\)). Supposons qu'un tel tuyau transporte un débit de 40,0 L/s, à partir d'une pression manométrique de 1,62 x 10 ⁶ N/m ². Le tuyau s'élève à 10,0 m le long d'une échelle jusqu'à une buse d'un diamètre intérieur de 3,00 cm. Quelle est la pression dans la buse ?

Figure\(\PageIndex{5}\) : La pression dans la buse de ce tuyau d'incendie est inférieure à celle du sol pour deux raisons : l'eau doit monter pour atteindre la buse et la vitesse augmente dans la buse. Malgré sa pression réduite, l'eau peut exercer une force importante sur tout objet qu'elle heurte grâce à son énergie cinétique. La pression dans le flux d'eau devient égale à la pression atmosphérique une fois qu'il émerge dans l'air.

Stratégie

Nous devons utiliser l'équation de Bernoulli pour résoudre la pression, car la profondeur n'est pas constante.

Solution

L'équation de Bernoulli est

\[p_{1} + \frac{1}{2} \rho v_{1}^{2} + \rho gh_{1} = p_{2} + \frac{1}{2} \rho v_{2}^{2} + \rho gh_{2} \nonumber \]

où les indices 1 et 2 se réfèrent aux conditions initiales au niveau du sol et aux conditions finales à l'intérieur de la buse, respectivement. Il faut d'abord trouver les vitesses v ₁ et v ₂. Puisque Q = A ₁ v ₁, on obtient

\[v_{1} = \frac{Q}{A_{1}} = \frac{40.0 \times 10^{-3}\; m^{3}/s}{\pi (3.20 \times 10^{-2}\; m)^{2}} = 12.4\; m/s \ldotp \nonumber\]

De même, nous trouvons

\[v_{2} = 56.6\; m/s \ldotp \nonumber\]

Cette vitesse assez élevée est utile pour atteindre le feu. Maintenant, en prenant h ₁ pour zéro, nous résolvons l'équation de Bernoulli pour p ₂ :

\[p_{2} = p_{1} + \frac{1}{2} \rho (v_{1}^{2} - v_{2}^{2}) - \rho gh_{2} \ldotp \nonumber\]

La substitution de valeurs connues donne

\[\begin{align*} p_{2} & = (1.62 \times 10^{6}\; N/m^{2}) + \frac{1}{2} (1000\; kg/m^{3}) [(12.4\; m/s)^{2} - (56.6\; m/s)^{2}] - (1000\; kg/m^{3})(9.80\; m/s^{2})(10.0\; m) \\ & = 0 \ldotp \end{align*}\]

L'importance

Cette valeur est une pression manométrique, puisque la pression initiale a été donnée sous forme de pression manométrique. Ainsi, la pression de la buse est égale à la pression atmosphérique comme il se doit, car l'eau sort dans l'atmosphère sans modification de ses conditions.