14.7 : Dynamique des fluides

Last updated
Save as PDF

Page ID: 191720

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objectifs d'apprentissage

Décrire les caractéristiques du débit
Calculer le débit
Décrire la relation entre le débit et la vitesse
Expliquer les conséquences de l'équation de continuité sur la conservation de la masse

La première partie de ce chapitre traitait de la statique des fluides, c'est-à-dire de l'étude des fluides au repos. Le reste de ce chapitre traite de la dynamique des fluides, c'est-à-dire de l'étude des fluides en mouvement. Même les formes les plus élémentaires de mouvements fluides peuvent être très complexes. Pour cette raison, nous limitons notre étude aux fluides idéaux dans de nombreux exemples. Un fluide idéal est un fluide dont la viscosité est négligeable. La viscosité est une mesure de la friction interne d'un fluide ; nous l'examinons plus en détail dans Viscosité et turbulence. Dans quelques exemples, nous examinons un fluide incompressible, pour lequel une force extrêmement importante est requise pour modifier le volume, car la densité d'un fluide incompressible est constante partout.

Caractéristiques du flux

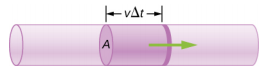
Les vecteurs de vitesse sont souvent utilisés pour illustrer le mouvement des fluides dans des applications telles que la météorologie. Par exemple, le vent, c'est-à-dire le mouvement fluide de l'air dans l'atmosphère, peut être représenté par des vecteurs indiquant la vitesse et la direction du vent à un point donné sur une carte. La figure$\PageIndex{1}$ montre des vecteurs de vitesse décrivant les vents lors de l'ouragan Arthur en 2014.

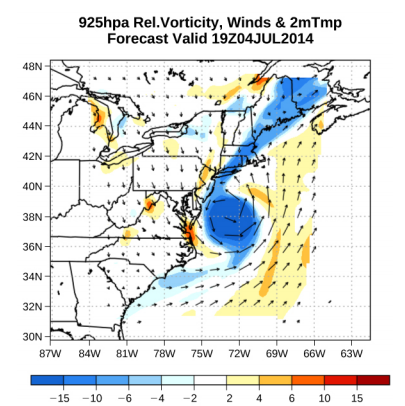
La figure est une carte de pression de l'ouragan Arthur qui remonte la côte est. Le centre de basse pression est indiqué par le point bleu. La vitesse du vent est maximale près du centre de basse pression et les vents se déplacent dans le sens antihoraire autour de celui-ci. — Figure$\PageIndex{1}$ : Les vecteurs de vitesse montrent le flux du vent lors de l'ouragan Arthur. Remarquez la circulation du vent autour de l'œil de l'ouragan. La vitesse du vent est maximale près de l'œil. Les couleurs représentent le tourbillon relatif, une mesure de la rotation ou de la rotation de l'air.

Une autre méthode pour représenter le mouvement d'un fluide est la rationalisation. Un canal représente la trajectoire d'un petit volume de fluide lorsqu'il s'écoule. La vitesse est toujours tangentielle à la ligne droite. Les diagrammes de la figure$\PageIndex{2}$ utilisent des courbes pour illustrer deux exemples de fluides se déplaçant dans un tuyau. Le premier fluide présente un écoulement laminaire (parfois décrit comme un flux constant), représenté par des lignes de courant lisses et parallèles. Notez que dans l'exemple illustré dans la partie (a), la vitesse du fluide est maximale au centre et diminue près des parois du tuyau en raison de la viscosité du fluide et du frottement entre les parois du tuyau et le fluide. Il s'agit d'un cas particulier d'écoulement laminaire, où le frottement entre le tuyau et le fluide est élevé, ce que l'on appelle des conditions limites d'absence de glissement. Le deuxième diagramme représente un écoulement turbulent, dans lequel les lignes de courant sont irrégulières et changent au fil du temps. Dans un écoulement turbulent, les trajets de l'écoulement du fluide sont irréguliers car différentes parties du fluide se mélangent ou forment de petites régions circulaires qui ressemblent à des tourbillons. Cela peut se produire lorsque la vitesse du fluide atteint une certaine vitesse critique.

La figure A est le schéma de l'écoulement laminaire représenté par des couches de fluide se déplaçant en lignes parallèles. La figure B est le schéma de l'écoulement turbulent représenté par des couches de fluide se déplaçant selon des trajectoires irrégulières et se heurtant. — Figure$\PageIndex{2}$ : (a) L'écoulement laminaire peut être considéré comme des couches de fluide se déplaçant suivant des trajectoires parallèles et régulières. (b) Dans un écoulement turbulent, les zones de fluide se déplacent selon des trajectoires irrégulières et en collision, ce qui entraîne un mélange et un tourbillonnement.

Le débit et sa relation avec la vitesse

Le volume de fluide passant par un endroit donné à travers une zone pendant une période donnée est appelé débit$Q$, ou plus précisément débit volumique. En symboles, cela s'écrit

\[Q = \frac{dV}{dt} \label{14.13}\]

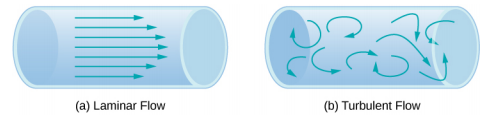
où$V$ est le volume et$t$ le temps écoulé. Sur la figure$\PageIndex{3}$, le volume du cylindre est$Ax$, donc le débit est

\[Q = \frac{dV}{dt} = \frac{d}{dt} (Ax) = A \frac{dx}{dt} = Av \ldotp\]

L'unité SI pour le débit est m ³ /s, mais plusieurs autres unités$Q$ sont couramment utilisées, telles que les litres par minute (L/min). Notez qu'un litre (L) est égal à 1/1000 de mètre cube ou 1000 centimètres cubes (10 ^{-3 m ³} ou 10 ³ cm ³).

La figure est un schéma d'un pipeline uniforme dont la section transversale est A. Le fluide s'écoule à travers le pipeline. Le volume de fluide V passe par un point P dans le temps t. — Figure$\PageIndex{3}$ : Le débit est le volume de fluide s'écoulant au-delà d'un point à travers la zone$A$ par unité de temps. Ici, le cylindre de fluide ombragé s'écoule au-delà d'un point$P$ dans un tuyau uniforme dans le temps$t$.

Le débit et la vitesse sont des grandeurs physiques liées, mais très différentes. Pour clarifier la distinction, considérez le débit d'une rivière. Plus la vitesse de l'eau est élevée, plus le débit de la rivière est élevé. Mais le débit dépend également de la taille et de la forme de la rivière. Un ruisseau de montagne rapide transporte beaucoup moins d'eau que le fleuve Amazone au Brésil, par exemple. La figure$\PageIndex{3}$ illustre le débit volumique. Le débit volumique est$Q = \frac{dV}{dt} = Av$, où A est la section transversale du tuyau et v est l'amplitude de la vitesse.

La relation précise entre le débit$Q$ et la vitesse moyenne$v$ est

\[Q = Av,\]

où$A$ est la surface transversale et$v$ la vitesse moyenne. La relation nous indique que le débit est directement proportionnel à la fois à la vitesse moyenne du fluide et à la surface transversale d'une rivière, d'un tuyau ou d'un autre conduit. Plus le conduit est grand, plus sa section transversale est grande. La figure$\PageIndex{3}$ montre comment cette relation est obtenue. Le cylindre ombré possède un volume$V = Ad$ qui s'écoule au-delà du point$P$ dans le temps$t$. Diviser les deux côtés de cette relation en$t$ donnant

\[\frac{V}{t} = \frac{Ad}{t} \ldotp \label{eq14.14A} \]

Nous le notons$Q = \frac{V}{t}$ et la vitesse moyenne est de$v = \frac{d}{t}$. Ainsi, l'équation \ ref {EQ14.14a} devient

\[Q = Av.\]

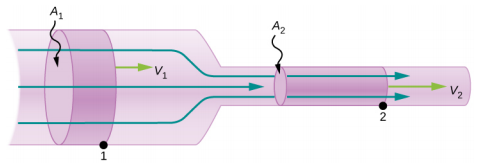
La figure$\PageIndex{4}$ montre un fluide incompressible s'écoulant le long d'un tuyau de rayon décroissant. Comme le fluide est incompressible, la même quantité de fluide doit s'écouler au-delà de n'importe quel point du tube dans un temps donné pour assurer la continuité du flux. Le flux est continu car il ne s'agit pas de sources ou de puits qui ajoutent ou éliminent de la masse. La masse qui entre dans le tuyau doit donc être égale à la masse sortant du tuyau. Dans ce cas, étant donné que la section transversale du tuyau diminue, la vitesse doit nécessairement augmenter. Cette logique peut être étendue pour dire que le débit doit être le même en tous points le long du tuyau. En particulier, pour les points arbitraires 1 et 2,

\[\begin{split} Q_{1} & = Q_{2}, \\ A_{1} v_{1} & = A_{2} v_{2} \ldotp \end{split} \label{14.14}\]

C'est ce que l'on appelle l'équation de continuité et elle est valable pour tout fluide incompressible (à densité constante). Les conséquences de l'équation de continuité peuvent être observées lorsque l'eau s'écoule d'un tuyau vers une buse de pulvérisation étroite : elle sort à grande vitesse, c'est le but de la buse. À l'inverse, lorsqu'une rivière se jette dans une extrémité d'un réservoir, l'eau ralentit considérablement, reprenant peut-être de la vitesse lorsqu'elle quitte l'autre extrémité du réservoir. En d'autres termes, la vitesse augmente lorsque la surface transversale diminue, et la vitesse diminue lorsque la surface transversale augmente.

La figure est le schéma d'un pipeline qui se rétrécit de la zone de section A1 à la zone de section A2. Le fluide s'écoule dans le pipeline. Le volume de fluide V1 passe par un point 1, situé au niveau de la partie à section transversale large, dans le temps t. Le volume de fluide V2 passe par un point 2, situé dans la partie à section étroite, dans le temps t. — Figure$\PageIndex{4}$ : Lorsqu'un tube se rétrécit, le même volume occupe une plus grande longueur. Pour qu'un même volume passe les points 1 et 2 en un temps donné, la vitesse doit être supérieure au point 2. Le processus est parfaitement réversible. Si le fluide s'écoule dans la direction opposée, sa vitesse diminue lorsque le tube s'élargit. (Notez que les volumes relatifs des deux cylindres et les flèches vectorielles de vitesse correspondantes ne sont pas dessinés à l'échelle.)

Les liquides étant essentiellement incompressibles, l'équation de continuité est valable pour tous les liquides. Cependant, les gaz étant compressibles, l'équation doit être appliquée avec prudence aux gaz s'ils sont soumis à une compression ou à une expansion.

Exemple 14.5 : Calcul de la vitesse du fluide à travers une buse

Une buse d'un diamètre de 0,500 cm est fixée à un tuyau d'arrosage d'un rayon de 0,900 cm. Le débit à travers le tuyau et la buse est de 0,500 L/s. Calculez la vitesse de l'eau :

dans le tuyau et
dans la buse.

Stratégie

Nous pouvons utiliser la relation entre le débit et la vitesse pour trouver les deux vitesses. Nous utilisons l'indice 1 pour le tuyau et 2 pour la buse.

Solution

Nous résolvons l'équation du débit pour la vitesse et l'utilisation$\pi r_{1}^{2}$ pour la section transversale du tuyau, en obtenant $$v = \ frac {Q} {A} = \ frac {Q} {\ pi r_ {1} ^ {2}} \ ldotp$$ La substitution de valeurs et l'utilisation de conversions d'unités appropriées donnent $$v = \ frac {(0,500 \ ; L/s) (10^ {-3} \ ; {m^ 3} /L)} {(3,14) (9,00 \ fois 10^ {-3} \ ; m) ^ {2} } = 1,96 \ ; m/s \ ldotp$$
Nous pourrions répéter ce calcul pour trouver la vitesse dans la buse v ₂, mais nous utilisons l'équation de continuité pour donner un aperçu quelque peu différent. L'équation indique que $$A_ {1} v_ {1} = A_ {2} v_ {2} \ LDotp$$Résoudre pour v ₂ et remplacer$\pi r^{2}$ la section transversale donne $$v_ {2} = \ frac {A_ {1}} {A_ {2}} v_ {1} = \ frac {\ pi r_ {1} ^ {2}} {2}} v_ {1}} {2}} v_ {1}} {2}} v_ {1} r_ {2} ^ {2}} v_ {1} = \ frac {r_ {1} ^ {2}} {r_ {2} ^ {2}} v_ {1} \ ldotp$$ Substituer des valeurs connues, $$v_ {2} = \ frac {(0,900 \ ; cm) ^ {2}} {(0,250 \ ; cm) ^ {2}} (1,96 \ ; m/s) = 25,5 \ ; m/s \ ldotp$$

L'importance

Une vitesse de 1,96 m/s convient à peu près à l'eau sortant d'un tuyau sans buse. La buse produit un flux beaucoup plus rapide simplement en restreignant le flux vers un tube plus étroit.

La solution de la dernière partie de l'exemple montre que la vitesse est inversement proportionnelle au carré du rayon du tube, ce qui produit des effets importants lorsque le rayon varie. On peut éteindre une bougie à une certaine distance, par exemple en pinçant les lèvres, alors qu'il est tout à fait inefficace de souffler sur une bougie la bouche grande ouverte.

Conservation de masse

Le débit d'un fluide peut également être décrit par le débit massique ou le débit massique. Il s'agit de la vitesse à laquelle une masse du fluide dépasse un point. Reportez-vous à nouveau à la Figure$\PageIndex{3}$, mais cette fois, considérez la masse dans le volume ombré. La masse peut être déterminée à partir de la densité et du volume :

\[m = \rho V = \rho Ax \ldotp\]

Le débit massique est alors

\[\frac{dm}{dt} = \frac{d}{dt} (\rho Ax) = \rho A \frac{dx}{dt} = \rho Av,\]

où$\rho$ est la densité, A est la surface transversale et v est l'amplitude de la vitesse. Le débit massique est une quantité importante dans la dynamique des fluides et peut être utilisé pour résoudre de nombreux problèmes. Considérez Figure$\PageIndex{5}$. Le tuyau de la figure commence à l'entrée avec une section transversale de A ₁ et se rétrécit jusqu'à une sortie avec une section transversale plus petite de A ₂. La masse de fluide entrant dans le tuyau doit être égale à la masse de fluide sortant du tuyau. Pour cette raison, la vitesse à la sortie (v ₂) est supérieure à la vitesse de l'entrée (v ₁). En utilisant le fait que la masse de fluide entrant dans le tuyau doit être égale à la masse de fluide sortant du tuyau, nous pouvons trouver une relation entre la vitesse et la section transversale en prenant le taux de variation de la masse entrante et sortante :

\[\begin{split} \left(\dfrac{dm}{dt}\right)_{1} & = \left(\dfrac{dm}{dt}\right)_{2} \\ \rho_{1} A_{1} v_{1} & = \rho_{2} A_{2} v_{2} \ldotp \end{split} \label{14.15}\]

L'équation \ ref {14.15} est également connue sous le nom d'équation de continuité sous sa forme générale. Si la densité du fluide reste constante pendant la constriction, c'est-à-dire que le fluide est incompressible, alors la densité s'annule à partir de l'équation de continuité,

\[A_{1} v_{1} = A_{2} v_{2} \ldotp\]

L'équation se réduit pour montrer que le débit volumique dans le tuyau est égal au débit volumique sortant du tuyau.

La figure est un schéma du fluide s'écoulant dans une conduite uniforme ayant la section transversale A. Le volume de fluide V delta t traverse la canalisation pendant le temps delta t. — Figure$\PageIndex{5}$ : Géométrie permettant de dériver l'équation de continuité. La quantité de liquide entrant dans la section transversale (ombrée) doit être égale à la quantité de liquide quittant la section transversale si le liquide est incompressible.