14.3 : Fluides, densité et pression (partie 2)

Last updated
Save as PDF

Page ID: 191695

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Variation de la pression en fonction de la profondeur dans un fluide de densité constante

La pression est définie pour tous les états de la matière, mais elle est particulièrement importante lorsqu'il s'agit de fluides. Une caractéristique importante des fluides est l'absence de résistance significative à la composante d'une force appliquée parallèlement à la surface d'un fluide. Les molécules du fluide s'écoulent simplement pour s'adapter à la force horizontale. Une force appliquée perpendiculairement à la surface comprime ou dilate le fluide. Si vous essayez de comprimer un fluide, vous constatez qu'une force de réaction se développe à chaque point intérieur du fluide vers l'extérieur, équilibrant ainsi la force appliquée sur les molécules à la limite.

Considérez un fluide de densité constante, comme indiqué sur la figure$\PageIndex{1}$. La pression au fond du récipient est due à la pression de l'atmosphère (p ₀) plus la pression due au poids du fluide. La pression due au fluide est égale au poids du fluide divisé par la surface. Le poids du fluide est égal à sa masse multipliée par l'accélération due à la gravité.

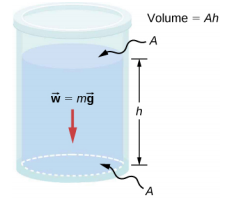
La figure A est un dessin d'un contenant. Le fond du récipient comporte une zone A. Le récipient est rempli de liquide à la hauteur h. Le texte à droite du récipient indique « Le volume est égal à A fois h. » — Figure$\PageIndex{1}$ : Le fond de ce récipient supporte la totalité du poids du liquide qu'il contient. Les côtés verticaux ne peuvent pas exercer de force ascendante sur le fluide (car celui-ci ne peut pas résister à une force de cisaillement), le fond doit donc tout supporter.

Comme la densité est constante, le poids peut être calculé à l'aide de la densité :

\[w = mg = \rho Vg = \rho Ahg \ldotp\]

La pression au fond du récipient est donc égale à la pression atmosphérique ajoutée au poids du fluide divisé par la surface :

\[p = p_{0} + \frac{\rho Ahg}{A} = p_{0} + \rho hg \ldotp\]

Cette équation n'est valable que pour la pression en profondeur pour un fluide de densité constante

Pression en profondeur pour un fluide de densité constante

La pression en profondeur dans un fluide de densité constante est égale à la pression de l'atmosphère plus la pression due au poids du fluide, ou

\[p = p_{0} + \rho hg, \label{14.4}\]

Où p est la pression à une profondeur donnée, p ₀ est la pression de l'atmosphère,$\rho$ est la densité du fluide, g est l'accélération due à la gravité et h est la profondeur.

Photo d'un barrage érigé sur une rivière. — Figure$\PageIndex{2}$ : Le barrage des Trois Gorges, érigé sur le fleuve Yangtsé, dans le centre de la Chine, en 2008, a créé un énorme réservoir qui a déplacé plus d'un million de personnes. (crédit : « Le Grand Portage » /Flickr)

Exemple 14.1 : À quelle force un barrage doit-il résister ?

Considérez la pression et la force qui s'exercent sur le barrage retenant un réservoir d'eau (Figure$\PageIndex{2}$). Supposons que le barrage ait une largeur de 500 m et que l'eau ait une profondeur de 80 m au niveau du barrage, comme illustré ci-dessous. a) Quelle est la pression moyenne exercée par l'eau sur le barrage ? (b) Calculez la force exercée contre le barrage.

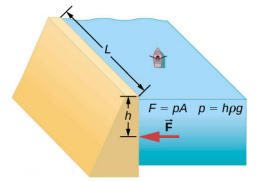
La figure est un dessin schématique d'un barrage de longueur L et de hauteur h érigé sur la rivière. Il y a un petit canot dans la rivière avec un seul passager. Les formules F est égale à p fois A et p est égal à h fois p fois g sont incluses dans cette illustration.

La pression moyenne p due au poids de l'eau est la pression à la profondeur moyenne h de 40,0 m, car la pression augmente linéairement avec la profondeur. La force exercée par l'eau sur le barrage est la pression moyenne multipliée par la surface de contact, F = pA.

Solution

La pression moyenne due au poids d'un fluide est de $$p = h \ rho g \ ldotp \ label {14.5} $En entrant la densité de l'eau dans le tableau 14.1 et en prenant h comme profondeur moyenne de 40,0 m, nous obtenons $$ \ begin {split} p & = (40,0 \ ; m) (10^ {3}} \ ; kg/m^ {3}) (9,80 \ ; m/s^ {2}) \ \ & = 3,92 \ fois 10^ {5} \ ; N/m^ {2} = 392 \ ; kPa \ ldotp \ end {split} $$
Nous avons déjà trouvé la valeur de p. La superficie du barrage est $$A = (80,0 \ ; m) \ times (500 \ ; m) = 4,00 \ fois 10^ {4} \ ; m^ {2} \ ldotp$so that $$ \ begin {split} F & = (3,92 \ times 10^ {5} \ ; N/m^ {2}) (4,00 \ times 10^ {4} \ ; m^ {2}) \ \ & = 1,57 \ fois 10^ {10} \ ; M \ ldotp \ end {split} $$

L'importance

Bien que cette force semble importante, elle est faible par rapport au poids de 1,96 x 10 ¹³ N de l'eau du réservoir. En fait, il ne représente que 0,0800 % du poids.

Exercice 14.1

Si le réservoir de l'exemple$\PageIndex{1}$ couvrait deux fois la superficie, mais était maintenu à la même profondeur, le barrage devrait-il être repensé ?

Pression dans un fluide statique dans un champ gravitationnel uniforme

Un fluide statique est un fluide qui n'est pas en mouvement. À n'importe quel point d'un fluide statique, la pression de tous les côtés doit être égale, sinon le fluide à ce point réagirait à une force nette et accélérerait.

La pression en tout point d'un fluide statique dépend uniquement de la profondeur à ce point. Comme nous l'avons vu, la pression dans un fluide proche de la Terre varie en fonction de la profondeur en raison du poids du fluide au-dessus d'un niveau donné. Dans les exemples ci-dessus, nous avons supposé que la densité était constante et que la densité moyenne du fluide était une bonne représentation de la densité. Il s'agit d'une approximation raisonnable pour les liquides tels que l'eau, où des forces importantes sont nécessaires pour comprimer le liquide ou modifier le volume. Dans une piscine, par exemple, la densité est approximativement constante et l'eau du fond est très peu comprimée par le poids de l'eau du dessus. Voyager dans l'atmosphère est une situation tout à fait différente, cependant. La densité de l'air commence à changer de manière significative à une courte distance au-dessus de la surface de la Terre.

Pour obtenir une formule de variation de la pression en$\rho$ fonction de la profondeur dans un réservoir contenant un fluide de densité à la surface de la Terre, nous devons partir de l'hypothèse que la densité du fluide n'est pas constante. Le fluide situé à des niveaux plus profonds est soumis à plus de force que le fluide plus proche de la surface en raison du poids du fluide au-dessus. Par conséquent, la pression calculée à une profondeur donnée est différente de la pression calculée à l'aide d'une densité constante.

Imaginez un mince élément de fluide à une profondeur h, comme indiqué sur la figure$\PageIndex{3}$. Supposons que l'élément ait une section transversale A et une hauteur$\Delta$ y. Les forces agissant sur l'élément sont dues aux pressions p (y) au-dessus et p (y +$\Delta$ y) en dessous. Le poids de l'élément lui-même est également indiqué sur le diagramme du corps libre.

La figure A est un dessin schématique d'un cylindre rempli de liquide et ouvert sur l'atmosphère sur sa partie supérieure. Un disque de masse Delta m, de surface A identique à la surface du cylindre et de hauteur Delta y est placé dans le fluide. Un fluide de hauteur h se trouve au-dessus du disque. La figure B est un schéma de la force Delta m x g exprimée par le disque, p (y) x A appliquée par le fluide au-dessus du disque et p (y + Delta y) x A appliquée par le fluide sous le disque. — Figure$\PageIndex{3}$ : Forces appliquées à un élément de masse à l'intérieur d'un fluide. Le poids de l'élément lui-même est indiqué sur le diagramme du corps libre.

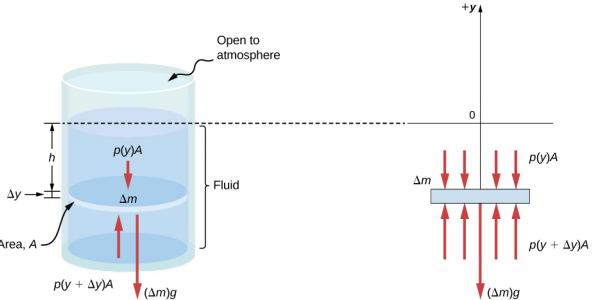
Comme l'élément de fluide compris entre y et y +$\Delta$ y n'accélère pas, les forces sont équilibrées. En utilisant un axe cartésien y orienté vers le haut, nous trouvons l'équation suivante pour la composante y :

\[p(y + \Delta y)A - p(y)A - g \Delta m = 0(\Delta y < 0) \ldotp \label{14.6}\]

Notez que si l'élément avait une composante d'accélération y non nulle, le côté droit ne serait pas nul mais serait plutôt la masse multipliée par l'accélération y. La masse de l'élément peut être écrite en termes de densité du fluide et de volume des éléments :

\[\Delta m = |\rho A \Delta y| = - \rho A \Delta y \quad (\Delta y < 0) \ldotp\]

En plaçant cette expression pour$\Delta$ m dans l'équation \ ref {14.6} puis en divisant les deux côtés par A$\Delta$ y, nous trouvons

\[\frac{p(y + \Delta y) - p(y)}{\Delta y} = - \rho g \ldotp \label{14.7}\]

En prenant la limite de l'élément infinitésimal$\Delta$ y → 0, nous obtenons l'équation différentielle suivante, qui donne la variation de pression dans un fluide :

\[\frac{dp}{dy} = - \rho g \ldotp \label{14.8}\]

Cette équation nous indique que le taux de variation de pression dans un fluide est proportionnel à la densité du fluide. La solution de cette équation dépend du fait que la densité$\rho$ est constante ou change avec la profondeur, c'est-à-dire de la fonction$\rho$ (y).

Si la plage de profondeur analysée n'est pas trop grande, on peut supposer que la densité est constante. Mais si la plage de profondeur est suffisamment grande pour que la densité varie sensiblement, comme dans le cas de l'atmosphère, la densité change de manière significative avec la profondeur. Dans ce cas, nous ne pouvons pas utiliser l'approximation d'une densité constante.

Pression dans un fluide à densité constante

Utilisons l'équation \ ref {14.9} pour élaborer une formule pour la pression à une profondeur h à partir de la surface d'un réservoir d'un liquide tel que de l'eau, où la densité du liquide peut être considérée comme constante.

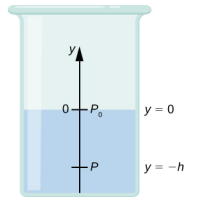
Schéma du bécher rempli de liquide à la hauteur h. Le fluide présente une pression P0 égale à zéro en surface et une pression P au fond du bécher.

Nous devons intégrer l'équation \ ref {14.9} de y = 0, où la pression est la pression atmosphérique (p ₀), à y = −h, la coordonnée y de la profondeur :

\[\begin{split} \int_{p_{0}}^{p} dp & = - \int_{0}^{-h} \rho gdy \\ p - p_{0} & = \rho gh \\ p & = p_{0} + \rho gh \ldotp \end{split} \label{14.9}\]

Ainsi, la pression à une profondeur de fluide à la surface de la Terre est égale à la pression atmosphérique plus$\rho$ gh si la densité du fluide est constante sur la hauteur, comme nous l'avons constaté précédemment.

Notez que la pression dans un fluide dépend uniquement de la profondeur par rapport à la surface et non de la forme du récipient. Ainsi, dans un récipient où un fluide peut se déplacer librement dans différentes parties, le liquide reste au même niveau dans chaque pièce, quelle que soit la forme, comme le montre la figure$\PageIndex{4}$.

Une photo de quelques récipients en verre de formes différentes reliés par un tube de verre au fond et remplis de liquide rouge. Le fluide se trouve à la même hauteur dans les différents récipients en verre. — Figure$\PageIndex{4}$ : Si un fluide peut s'écouler librement entre les parties d'un récipient, il s'élève à la même hauteur dans chaque partie. Dans le récipient illustré, la pression au bas de chaque colonne est la même ; si elle n'était pas la même, le fluide circulerait jusqu'à ce que les pressions soient égales.

Variation de la pression atmosphérique avec la hauteur

L'évolution de la pression atmosphérique en fonction de l'altitude est particulièrement intéressante. En supposant que la température de l'air soit constante et que la loi des gaz idéale de la thermodynamique décrit l'atmosphère avec une bonne approximation, nous pouvons trouver la variation de la pression atmosphérique en fonction de la hauteur, lorsque la température est constante. (Nous discuterons de la loi idéale sur les gaz dans un chapitre ultérieur, mais nous supposons que vous la connaissez déjà au lycée et en chimie.) Soit p (y) la pression atmosphérique à la hauteur y. La densité$\rho$ à y, la température T sur l'échelle Kelvin (K) et la masse m d'une molécule d'air sont liées à la pression absolue par la loi des gaz idéaux, sous la forme

\[p = \rho \frac{k_{B} T}{m}\; (atmosphere), \label{14.10}\]

où k _B est la constante de Boltzmann, qui a une valeur de 1,38 x 10 ⁻²³ J/K.

Vous avez peut-être rencontré la loi des gaz idéale sous la forme pV = nRT, où n est le nombre de moles et R est la constante du gaz. Ici, la même loi a été écrite sous une forme différente, en utilisant la densité$\rho$ au lieu du volume V. Par conséquent, si la pression p change avec la hauteur, la densité change également$\rho$. En utilisant la densité issue de la loi des gaz idéaux, le taux de variation de la pression en fonction de la hauteur est donné comme

\[\frac{dp}{dy} = -p \left(\dfrac{mg}{k_{B} T}\right),\]

où des quantités constantes ont été collectées entre parenthèses. En remplaçant ces constantes par un symbole unique$\alpha$, l'équation semble beaucoup plus simple :

\[\begin{split} \frac{dp}{dy} & = - \alpha p \\ \frac{dp}{p} & = - \alpha dy \\ \int_{p_{0}}^{p(y)} \frac{dp}{p} & = \int_{0}^{y} - \alpha dy \\ [\ln (p)]_{p_{0}}^{p(y)} & = [- \alpha y]_{0}^{y} \\ \ln (p) - \ln (p_{0}) & = - \alpha y \\ \ln \left(\dfrac{p}{p_{0}}\right) & = - \alpha y \end{split}\]

Cela donne la solution

\[p(y) = p_{0} e^{- \alpha y} \ldotp\]

Ainsi, la pression atmosphérique baisse de façon exponentielle avec l'altitude, puisque l'axe y est pointé vers le haut depuis le sol et que y a des valeurs positives dans l'atmosphère au-dessus du niveau de la mer. La pression diminue d'un facteur selon lequel$\frac{1}{e}$ la hauteur est$\frac{1}{\alpha}$, ce qui nous donne une interprétation physique pour$\alpha$ : La constante$\frac{1}{\alpha}$ est une échelle de longueur qui caractérise la façon dont la pression varie avec la hauteur et est souvent appelée hauteur de l'échelle de pression.

Nous pouvons obtenir une valeur approximative de en$\alpha$ utilisant la masse d'une molécule d'azote comme indicateur d'une molécule d'air. À une température de 27 °C, soit 300 K, on trouve

\[\alpha = - \frac{mg}{k_{B} T} = \frac{(4.8 \times 10^{-26}\; kg) \times (9.81\; m/s^{2})}{(1.38 \times 10^{-23}\; J/K) \times (300\; K)} = \frac{1}{8800\; m} \ldotp\]

Par conséquent, pour chaque 8800 mètres, la pression de l'air baisse d'un facteur 1/e, soit environ un tiers de sa valeur. Cela ne nous donne qu'une estimation approximative de la situation réelle, puisque nous avons supposé à la fois une température constante et une constante g sur de si grandes distances de la Terre, ce qui n'est pas correct en réalité.

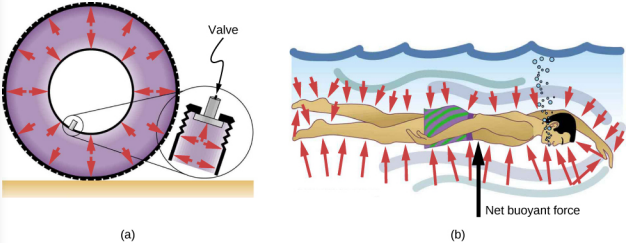
Direction de la pression dans un fluide

La pression du fluide n'a pas de direction, étant une quantité scalaire, tandis que les forces dues à la pression ont des directions bien définies : elles s'exercent toujours perpendiculairement à n'importe quelle surface. La raison en est que les fluides ne peuvent pas résister ou exercer des forces de cisaillement. Ainsi, dans un fluide statique enfermé dans un réservoir, la force exercée sur les parois du réservoir s'exerce perpendiculairement à la surface intérieure. De même, la pression est exercée perpendiculairement aux surfaces de tout objet à l'intérieur du fluide. La figure$\PageIndex{5}$ illustre la pression exercée par l'air sur les parois d'un pneu et par l'eau sur le corps d'un nageur.

La figure A est un schéma d'un pneu rempli d'air. La pression à l'intérieur de ce pneu exerce des forces perpendiculaires à toutes les surfaces en contact, y compris la valve. La figure B est un dessin schématique d'un nageur sous l'eau. La pression est exercée perpendiculairement à tous les côtés de ce nageur avec une force de flottabilité nette plus importante sous le nageur. — Figure$\PageIndex{5}$ : (a) La pression à l'intérieur de ce pneu exerce des forces perpendiculaires à toutes les surfaces avec lesquelles il entre en contact. Les flèches représentent les directions et les amplitudes des forces exercées en différents points. (b) Une pression est exercée perpendiculairement de tous les côtés de ce nageur, car l'eau s'écoulerait dans l'espace qu'il occupe s'il n'était pas là. Les flèches représentent les directions et les amplitudes des forces exercées en différents points sur le nageur. Notez que les forces sont plus importantes en dessous, en raison de la plus grande profondeur, ce qui donne une force nette vers le haut ou de flottabilité. La force verticale nette exercée sur le nageur est égale à la somme de la force de flottabilité et du poids du nageur.