13.8 : La théorie de la gravité d'Einstein

Objectifs d'apprentissage

• Décrire comment la théorie de la relativité générale aborde la gravitation
• Expliquer le principe d'équivalence
• Calculer le rayon de Schwarzschild d'un objet
• Résumez les preuves de la présence de trous noirs

La loi de la gravitation universelle de Newton prédit avec précision une grande partie de ce que nous voyons dans notre système solaire. En effet, seules les lois de Newton ont été nécessaires pour envoyer avec précision chaque véhicule spatial lors de son voyage. La trajectoire des astéroïdes qui traversent la Terre et de la plupart des autres objets célestes peut être déterminée avec précision uniquement à l'aide des lois de Newton. Néanmoins, de nombreux phénomènes ont montré une différence par rapport à ce que prédisent les lois de Newton, notamment l'orbite de Mercure et l'effet de la gravité sur la lumière. Dans cette section, nous examinons une autre façon d'envisager la gravitation.

Une révolution en perspective

En 1905, Albert Einstein a publié sa théorie de la relativité spéciale. Cette théorie est discutée en détail dans la Relativité, nous ne disons donc que quelques mots ici. Selon cette théorie, aucun mouvement ne peut dépasser la vitesse de la lumière : c'est la limite de vitesse de l'Univers. Ce simple fait a été vérifié dans d'innombrables expériences. Cependant, cela a des conséquences incroyables : l'espace et le temps ne sont plus absolus. Deux personnes qui se déplacent l'une par rapport à l'autre ne s'entendent pas sur la longueur des objets ni sur le passage du temps. Presque toutes les mécaniques que vous avez apprises dans les chapitres précédents, bien qu'elles soient remarquablement précises, même à des vitesses de plusieurs milliers de kilomètres par seconde, commencent à échouer à l'approche de la vitesse de la lumière.

Cette limite de vitesse dans l'Univers remettait également en question l'hypothèse inhérente à la loi de la gravitation de Newton selon laquelle la gravité est une force agissant à distance. C'est-à-dire que, sans contact physique, tout changement de position d'une masse est instantanément communiqué à toutes les autres masses. Cette hypothèse ne provient d'aucun principe premier, car la théorie de Newton ne répond tout simplement pas à la question. (On pensait également à la même chose des forces électromagnétiques. Il est juste de dire que la plupart des scientifiques n'étaient pas tout à fait à l'aise avec le concept d'action à distance.)

Une deuxième hypothèse apparaît également dans l'équation 13.2.1 de la loi de la gravitation de Newton. Les masses sont supposées être exactement les mêmes que celles utilisées dans la deuxième loi de Newton,\(\vec{F}\) =\(\vec{a}\) m. Nous avons fait cette hypothèse dans bon nombre de nos dérivations dans ce chapitre. Encore une fois, il n'existe aucun principe sous-jacent selon lequel cela doit être le cas, mais les résultats expérimentaux sont conformes à cette hypothèse. Dans la théorie ultérieure de la relativité générale d'Einstein (1916), ces deux questions ont été abordées. Sa théorie portait sur la géométrie de l'espace-temps et sur la façon dont la masse (et l'accélération) se déforment et interagissent avec cet espace-temps. Ce n'était pas une théorie des forces gravitationnelles. Les mathématiques de la théorie générale dépassent le cadre de ce texte, mais nous pouvons examiner certains principes sous-jacents et leurs conséquences.

Le principe d'équivalence

Einstein est arrivé à sa théorie générale en partie en se demandant pourquoi une personne qui tombait librement ne sentait pas son poids. En effet, il est courant de dire que les astronautes en orbite autour de la Terre sont en apesanteur, malgré le fait que la gravité de la Terre y soit encore très forte. Selon la théorie générale d'Einstein, il n'y a aucune différence entre la chute libre et l'apesanteur. C'est ce qu'on appelle le principe d'équivalence. Le corollaire tout aussi surprenant est qu'il n'y a aucune différence entre un champ gravitationnel uniforme et une accélération uniforme en l'absence de gravité. Concentrons-nous sur cette dernière déclaration. Bien qu'un champ gravitationnel parfaitement uniforme ne soit pas réalisable, nous pouvons très bien l'approximer.

Dans un laboratoire de taille raisonnable sur Terre, le champ gravitationnel\(\vec{g}\) est essentiellement uniforme. Le corollaire indique que toutes les expériences physiques qui y sont effectuées donnent les mêmes résultats que celles effectuées en laboratoire en accélérant\(\vec{a} = \vec{g}\) dans l'espace lointain, loin de toutes les autres masses. La figure\(\PageIndex{1}\) illustre le concept.

Figure\(\PageIndex{1}\) : Selon le principe d'équivalence, les résultats de toutes les expériences effectuées en laboratoire dans un champ gravitationnel uniforme sont identiques aux résultats des mêmes expériences effectuées dans un laboratoire à accélération uniforme.

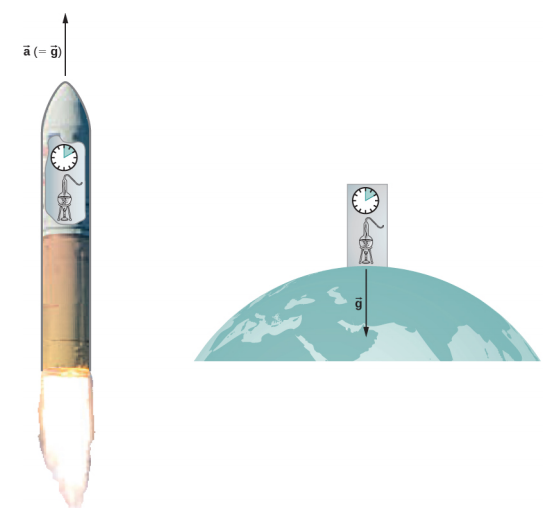
Comment ces deux situations apparemment fondamentalement différentes peuvent-elles être identiques ? La réponse est que la gravitation n'est pas une force entre deux objets mais le résultat de la réponse de chaque objet à l'effet que l'autre a sur l'espace-temps qui l'entoure. Un champ gravitationnel uniforme et une accélération uniforme ont exactement le même effet sur l'espace-temps.

Une théorie géométrique de la gravité

La géométrie euclidienne suppose un espace « plat » dans lequel, parmi les attributs les plus connus, une ligne droite est la distance la plus courte entre deux points, la somme des angles de tous les triangles doit être de 180 degrés et les lignes parallèles ne se croisent jamais. La géométrie non euclidienne n'a été sérieusement étudiée qu'au XIXe siècle, il n'est donc pas surprenant que l'espace euclidien soit intrinsèquement supposé dans toutes les lois de Newton.

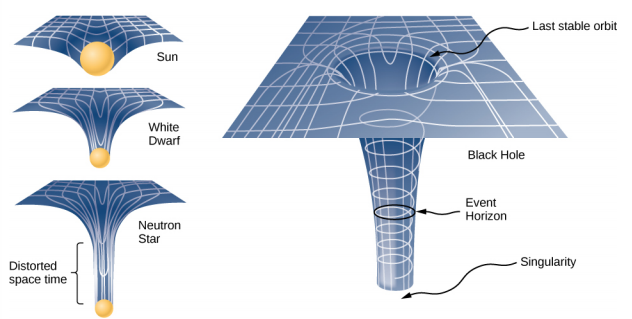
La théorie générale de la relativité remet en question cette hypothèse de longue date. Seul l'espace vide est plat. La présence de masse, ou d'énergie, puisque la relativité ne fait pas de distinction entre les deux, déforme ou courbe l'espace et le temps, ou l'espace-temps, autour d'elle. Le mouvement de toute autre masse est simplement une réponse à cet espace-temps incurvé. La figure\(\PageIndex{2}\) est une représentation bidimensionnelle d'une masse plus petite orbitant en réponse à l'espace déformé créé par la présence d'une masse plus grande. Dans une image plus précise mais confuse, nous verrions également l'espace déformé par la masse orbitale, et les deux masses seraient en mouvement en réponse à la distorsion totale de l'espace. Notez que la figure est une représentation qui permet de visualiser le concept. Ce sont des distorsions de notre espace et de notre temps tridimensionnels. Nous ne les voyons pas comme nous le ferions avec une fossette sur une balle. Nous ne voyons la distorsion que par des mesures minutieuses du mouvement des objets et de la lumière lorsqu'ils se déplacent dans l'espace.

Figure\(\PageIndex{2}\) : Une masse plus petite orbitant dans l'espace-temps déformé d'une masse plus grande. En fait, toute masse ou énergie déforme l'espace-temps.

Pour les champs gravitationnels faibles, les résultats de la relativité générale ne diffèrent pas significativement de la loi de gravitation de Newton. Mais pour les champs gravitationnels intenses, les résultats divergent et il a été démontré que la relativité générale permet de prédire les bons résultats. Même dans le champ gravitationnel relativement faible de notre Soleil à la distance de l'orbite de Mercure, nous pouvons observer l'effet. À partir du milieu des années 1800, l'orbite elliptique de Mercure a été soigneusement mesurée. Cependant, bien qu'elle soit elliptique, son mouvement est compliqué par le fait que la position périhéliale de l'ellipse avance lentement. La majeure partie de cette avancée est due à l'attraction gravitationnelle d'autres planètes, mais une petite partie de cette avancée n'a pas pu être expliquée par la loi de Newton. À un moment donné, il y a même eu la recherche d'une planète « compagne » qui expliquerait cet écart. Mais la relativité générale prédit correctement les mesures. Depuis lors, de nombreuses mesures, telles que la déflexion de la lumière d'objets éloignés par le Soleil, ont permis de vérifier que la relativité générale prédit correctement les observations.

Nous clôturons cette discussion par un dernier commentaire. Nous avons souvent fait référence à des distorsions de l'espace-temps ou à des distorsions dans l'espace et dans le temps. Dans la relativité spéciale comme dans la relativité générale, la dimension du temps est sur un pied d'égalité avec chaque dimension spatiale (sa place ne diffère dans les deux théories que par un facteur d'échelle finalement sans importance). À proximité d'une très grande masse, non seulement l'espace voisin est « étiré », mais le temps est dilaté ou « ralenti ». Nous aborderons ces effets plus en détail dans la section suivante.

Trous noirs

La théorie de la gravitation d'Einstein est exprimée dans une équation tensorielle d'une simplicité trompeuse (les tenseurs sont une généralisation de scalaires et de vecteurs), qui exprime la façon dont une masse détermine la courbure de l'espace-temps qui l'entoure. Les solutions à cette équation produisent l'une des prédictions les plus fascinantes : le trou noir. La prédiction est que si un objet est suffisamment dense, il s'effondrera sur lui-même et sera entouré d'un horizon d'événements auquel rien ne pourra s'échapper. Le nom « trou noir », inventé par l'astronome John Wheeler en 1969, fait référence au fait que la lumière ne peut pas s'échapper d'un tel objet. Karl Schwarzschild a été le premier à remarquer ce phénomène en 1916, mais à cette époque, il était principalement considéré comme une curiosité mathématique.

Étonnamment, l'idée d'un corps massif auquel la lumière ne peut s'échapper remonte à la fin des années 1700. Indépendamment, John Michell et Pierre Simon Laplace ont utilisé la loi de gravitation de Newton pour montrer que la lumière quittant la surface d'une étoile de masse suffisante ne pouvait pas s'échapper. Leur travail était basé sur le fait que la vitesse de la lumière avait été mesurée par Ole Roemer en 1676. Il a noté des divergences dans les données relatives à la période orbitale de la lune Io à propos de Jupiter. Roemer s'est rendu compte que la différence provenait des positions relatives de la Terre et de Jupiter à différents moments et qu'il pouvait trouver la vitesse de la lumière à partir de cette différence. Michell et Laplace ont tous deux réalisé que, comme la lumière avait une vitesse limitée, il pouvait y avoir une étoile suffisamment massive pour que sa vitesse de fuite de sa surface puisse dépasser cette vitesse. Ainsi, la lumière retomberait toujours vers l'étoile. Curieusement, les observateurs suffisamment éloignés des plus grandes étoiles ne seraient pas en mesure de les voir, alors qu'ils pourraient voir une étoile plus petite à la même distance.

Rappelons que dans Énergie potentielle gravitationnelle et Énergie totale, nous avons constaté que la vitesse d'échappement, donnée par\(v_{\mathrm{esc}}=\sqrt{\frac{2 G M}{R}}\), est indépendante de la masse de l'objet qui s'échappe. Même si la nature de la lumière n'était pas entièrement comprise à l'époque, la masse de lumière, si elle en avait une, n'était pas pertinente. Par conséquent, cette équation devrait être valable pour la lumière. En substituant c, la vitesse de la lumière, à la vitesse d'échappement, nous avons

\[v_{esc} = c = \sqrt{\dfrac{2GM}{R}} \ldotp\]

Ainsi, nous n'avons besoin que de valeurs pour R et M telles que la vitesse d'échappement dépasse c, et la lumière ne pourra alors pas s'échapper. Michell a émis l'hypothèse que si une étoile avait la densité de notre Soleil et un rayon qui s'étendait juste au-delà de l'orbite de Mars, la lumière ne pourrait pas s'échapper de sa surface. Il a également émis l'hypothèse que nous serions toujours en mesure de détecter une telle étoile grâce à l'effet gravitationnel qu'elle aurait sur les objets qui l'entourent. C'était une conclusion éclairante, car c'est précisément ainsi que nous déduisons l'existence de tels objets aujourd'hui. Bien que nous n'ayons pas encore visité de trou noir, et que nous ne le ferons peut-être jamais, les preuves circonstancielles sont devenues si convaincantes que peu d'astronomes doutent de leur existence.

Avant d'examiner certaines de ces preuves, nous revenons à la solution de Schwarzschild à l'équation tensorielle issue de la relativité générale. Dans cette solution apparaît un rayon critique, aujourd'hui appelé rayon de Schwarzschild (R _S). Pour toute masse M, si cette masse est comprimée au point que son rayon devient inférieur au rayon de Schwarzschild, alors la masse s'effondrera en une singularité, et tout ce qui passe à l'intérieur de ce rayon ne peut pas s'échapper. Une fois à l'intérieur de R _S, la flèche du temps amène tout jusqu'à la singularité. (Au sens mathématique large, une singularité est l'endroit où la valeur d'une fonction va à l'infini. Dans ce cas, il s'agit d'un point de l'espace de volume nul avec une masse finie. Ainsi, la densité de masse et l'énergie gravitationnelle deviennent infinies.) Le rayon de Schwarzschild est donné par

\[R_{S} = \dfrac{2GM}{c^{2}} \ldotp \label{13.12}\]

Si vous regardez notre équation de vitesse d'échappement avec v _esc = c, vous remarquerez qu'elle donne précisément ce résultat. Mais il ne s'agit là que d'un accident fortuit causé par plusieurs hypothèses erronées. L'une de ces hypothèses est l'utilisation d'une expression classique incorrecte pour l'énergie cinétique de la lumière. Quelle est la densité d'un objet pour se transformer en trou noir ?

Exemple\(\PageIndex{1}\): Calculating the Schwarzschild Radius

Calculez le rayon de Schwarzschild pour le Soleil et la Terre. Comparez la densité du noyau d'un atome à la densité requise pour comprimer uniformément la masse de la Terre selon son rayon de Schwarzschild. La densité d'un noyau est d'environ 2,3 x 10 ¹⁷ kg/m ³.

Stratégie

Nous utilisons l'équation \ ref {13.12} pour ce calcul. Nous n'avons besoin que des masses de la Terre et du Soleil, que nous obtenons à partir des données astronomiques présentées à l'annexe D.

Solution

En substituant la masse du Soleil, nous avons

\[R_{S} = \dfrac{2GM}{c^{2}} = \dfrac{2(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(1.99 \times 10^{30}\; kg)}{(3.0 \times 10^{8}\; m/s)^{2}} = 2.95 \times 10^{3}\; m \ldotp\]

Il s'agit d'un diamètre d'environ 6 km seulement. Si l'on utilise la masse de la Terre, on obtient R _S = 8,85 x 10 ^-3 m, soit un diamètre inférieur à 2 cm ! Si nous regroupons la masse de la Terre dans une sphère de rayon R _S = 8,85 x 10 ^-3 m, nous obtenons une densité de

\[\rho = \dfrac{mass}{volume} = \dfrac{5.97 \times 10^{24}\; kg}{\dfrac{4}{3} \pi (8.85 \times 10^{-3}\; m)^{3}} = 2.06 \times 10^{30}\; kg/m^{3} \ldotp\]

L'importance

Une étoile à neutrons est l'objet le plus compact connu, en dehors du trou noir lui-même. L'étoile à neutrons est composée de neutrons ayant la densité d'un noyau atomique et, comme de nombreux trous noirs, on pense qu'elle est le vestige d'une supernova, une étoile qui explose à la fin de sa vie. Pour créer un trou noir à partir de la Terre, il faudrait le comprimer à une densité de treize ordres de grandeur supérieure à celle d'une étoile à neutrons. Ce processus exigerait une force inimaginable. Il n'existe aucun mécanisme connu qui pourrait transformer un objet de la taille de la Terre en trou noir. Pour le Soleil, vous devriez être capable de montrer qu'il devrait être comprimé à une densité environ 80 fois supérieure à celle d'un noyau. (Remarque : une fois que la masse est comprimée dans son rayon de Schwarzschild, la relativité générale veut qu'elle s'effondre jusqu'à devenir une singularité. Ces calculs montrent simplement la densité que nous devons atteindre pour initier cet effondrement.)

Exercices\(\PageIndex{1}\)

Considérez la densité requise pour faire de la Terre un trou noir par rapport à celle requise pour le Soleil. Quelle conclusion pouvez-vous tirer de cette comparaison quant à ce qui serait nécessaire pour créer un trou noir ? Vous attendriez-vous à ce que l'Univers comporte de nombreux trous noirs de faible masse ?

L'horizon des événements

Le rayon de Schwarzschild est également appelé horizon des événements d'un trou noir. Nous avons remarqué que l'espace et le temps s'étendent à proximité d'objets massifs, tels que des trous noirs. La figure\(\PageIndex{3}\) illustre cet effet sur l'espace. La distorsion causée par notre Soleil est en fait très faible et le diagramme est exagéré pour plus de clarté. Prenons l'exemple de l'étoile à neutrons\(\PageIndex{1}\). Bien que la distorsion de l'espace-temps à la surface d'une étoile à neutrons soit très élevée, son rayon est toujours plus grand que son rayon de Schwarzschild. Des objets pouvaient encore s'échapper de sa surface.

Cependant, si une étoile à neutrons gagne de la masse, elle finira par s'effondrer et se rétrécir au-delà du rayon de Schwarzschild. Une fois que cela se produira, toute la masse serait inévitablement attirée vers une singularité. Dans le diagramme, l'espace est étendu à l'infini. Le temps est également étiré à l'infini. À mesure que les objets tombent vers l'horizon des événements, nous les voyons s'approcher de plus en plus lentement, mais jamais atteindre l'horizon des événements. En tant qu'observateurs extérieurs, nous ne voyons jamais d'objets traverser l'horizon des événements. En fait, le temps s'arrête.

Simulation

Visitez ce site pour voir un exemple animé de ces distorsions spatiales.

Figure\(\PageIndex{3}\) : La distorsion spatiale devient plus perceptible à proximité de masses de plus en plus grandes. Une fois que la densité de masse atteint un niveau critique, un trou noir se forme et le tissu de l'espace-temps est déchiré. La courbure de l'espace est maximale à la surface de chacun des trois premiers objets représentés et est finie. La courbure diminue ensuite (non illustrée) jusqu'à zéro lorsque vous vous déplacez vers le centre de l'objet. Mais le trou noir est différent. La courbure devient infinie : la surface s'est réduite à une singularité et le cône s'étend à l'infini. (Remarque : Ces diagrammes ne sont pas présentés à n'importe quelle échelle.)

Les preuves de l'existence de trous noirs

Ce n'est que dans les années 1960, lorsque la première étoile à neutrons a été découverte, que l'intérêt pour l'existence des trous noirs s'est renouvelé. Les preuves de la présence de trous noirs sont basées sur plusieurs types d'observations, telles que l'analyse radiologique des binaires des rayons X, la lentille gravitationnelle de la lumière provenant de galaxies lointaines et le mouvement d'objets visibles autour de partenaires invisibles. Nous nous concentrerons sur ces observations ultérieures dans la mesure où elles se rapportent à ce que nous avons appris dans ce chapitre. Bien que la lumière ne puisse pas s'échapper d'un trou noir pour que nous puissions la voir, nous pouvons néanmoins constater l'effet gravitationnel du trou noir sur les masses environnantes.

La preuve la plus proche, et peut-être la plus spectaculaire, de la présence d'un trou noir se trouve au centre de notre galaxie de la Voie lactée. Le groupe galactique de l'UCLA, à l'aide des données obtenues par les télescopes W. M. Keck, a déterminé les orbites de plusieurs étoiles proches du centre de notre galaxie. Certaines de ces données sont présentées dans la figure\(\PageIndex{4}\). Les orbites de deux étoiles sont mises en évidence. À partir des mesures des périodes et de la taille de leurs orbites, on estime qu'ils orbitent autour d'une masse d'environ 4 millions de masses solaires. Notez que la masse doit résider dans la région créée par l'intersection des ellipses des étoiles. La région dans laquelle cette masse doit résider se situerait à l'intérieur de l'orbite de Mercure, mais rien n'y est visible dans le spectre visible.

Figure\(\PageIndex{4}\) : Trajectoires d'étoiles orbitant autour d'une masse au centre de notre galaxie de la Voie lactée. D'après leur mouvement, on estime qu'un trou noir d'environ 4 millions de masses solaires se trouve au centre. (crédit : UCLA Galactic Center Group — Équipe laser de l'Observatoire W.M. Keck)

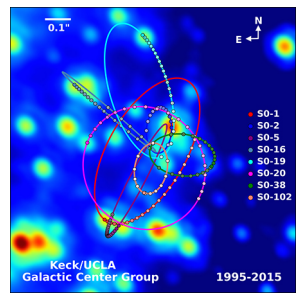
La physique de la création et de l'évolution des étoiles est bien établie. La source d'énergie ultime qui fait briller les étoiles est l'énergie auto-gravitationnelle qui déclenche la fusion. Le comportement général est que plus une étoile est massive, plus elle brille et plus sa durée de vie est courte. L'inférence logique est qu'une masse qui représente 4 millions de fois la masse de notre Soleil, confinée à une très petite région et qui ne peut être vue, n'a pas d'autre interprétation viable qu'un trou noir. Les observations extragalactiques suggèrent fortement que les trous noirs sont courants au centre des galaxies.

Visitez la page principale de l'UCLA Galactic Center Group pour obtenir des informations sur les binaires à rayons X et les lentilles gravitationnelles. Visitez cette page pour visualiser une visualisation tridimensionnelle des étoiles orbitant près du centre de notre galaxie, l'animation se trouvant au bas de la page.

Matière noire

Les étoiles orbitant près du cœur même de notre galaxie fournissent des preuves solides de la présence d'un trou noir à cet endroit, mais les orbites d'étoiles éloignées du centre suggèrent un autre phénomène intrigant qui est également observé indirectement. Rappelons que dans Gravitation près de la surface de la Terre, nous pouvons considérer la masse des objets sphériques situés en un point central pour calculer leurs effets gravitationnels sur d'autres masses. De même, nous pouvons traiter la masse totale qui se trouve sur l'orbite de n'importe quelle étoile de notre galaxie comme étant située au centre du disque de la Voie lactée. Nous pouvons estimer cette masse en comptant les étoiles visibles et inclure également dans notre estimation la masse du trou noir au centre.

Mais ce faisant, nous découvrons que la vitesse orbitale des étoiles est bien trop rapide pour être causée par une telle quantité de matière. La figure\(\PageIndex{5}\) montre les vitesses orbitales des étoiles en fonction de leur distance par rapport au centre de la Voie lactée. La ligne bleue représente les vitesses que nous pouvons attendre de nos estimations de la masse, tandis que la courbe verte correspond à ce que nous obtenons à partir de mesures directes. Apparemment, il y a beaucoup de matière que nous ne voyons pas, estimée à environ cinq fois plus que ce que nous voyons. Elle a donc été surnommée matière noire. De plus, le profil de vitesse ne correspond pas à ce que nous attendons de la distribution observée des étoiles visibles. Non seulement l'estimation de la masse totale n'est pas conforme aux données, mais la distribution attendue est également incohérente. Et ce phénomène ne se limite pas à notre galaxie, mais semble appartenir à toutes les galaxies. En fait, le problème a été remarqué pour la première fois dans les années 1930, lorsque des galaxies au sein d'amas ont été mesurées comme orbitant autour du centre de masse de ces amas plus rapidement qu'elles ne le devraient sur la base d'estimations de masse visible.

Figure\(\PageIndex{5}\) : La courbe bleue montre la vitesse orbitale attendue des étoiles de la Voie lactée sur la base des étoiles visibles que nous pouvons voir. La courbe verte indique que les vitesses réelles sont plus élevées, ce qui suggère de la matière supplémentaire invisible. (source : modification de l'œuvre de Matthew Newby)

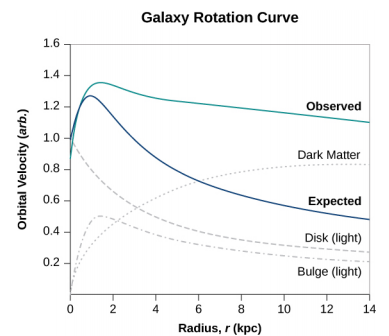
Il existe deux idées dominantes sur ce que cette question pourrait être : les Wimps et les MacHos. WIMPS est l'abréviation de particules massives qui interagissent faiblement. Ces particules (les neutrinos en sont un exemple) interagissent très faiblement avec la matière ordinaire et sont donc très difficiles à détecter directement. MacHos est l'acronyme d'objets halos compacts et massifs, composés de matière baryonique ordinaire, telle que des neutrons et des protons. Ces deux idées soulèvent des problèmes non résolus et de nombreuses recherches supplémentaires seront nécessaires pour résoudre le mystère.