13.E : Gravitation (exercices)

Questions conceptuelles

13.1 La loi de Newton sur la gravitation universelle

1. L'action à distance, comme c'est le cas pour la gravité, était autrefois considérée comme illogique et donc fausse. Quel est le déterminant ultime de la vérité en science, et pourquoi cette action à distance a-t-elle finalement été acceptée ?
2. Dans la loi de la gravitation universelle, Newton a supposé que la force était proportionnelle au produit des deux masses (~m ₁ m ₂). Bien que toutes les conjectures scientifiques doivent être vérifiées expérimentalement, pouvez-vous fournir des arguments pour expliquer pourquoi cela doit être le cas ? (Vous pouvez prendre en compte des exemples simples dans lesquels toute autre forme conduirait à des résultats contradictoires.)

13.2 Gravitation près de la surface de la Terre

3. Les ingénieurs doivent-ils tenir compte de la rotation de la Terre lorsqu'ils construisent de très hauts bâtiments à un endroit autre que l'équateur ou très près des pôles ?

13.3 Énergie potentielle gravitationnelle et énergie totale

4. Il a été indiqué qu'un satellite dont l'énergie totale est négative se trouve sur une orbite liée, alors qu'un satellite dont l'énergie totale est nulle ou positive se trouve sur une orbite illimitée. Pourquoi est-ce vrai ? Quel choix a été fait pour l'énergie potentielle gravitationnelle de telle sorte que cela soit vrai ?
5. Il a été démontré que l'énergie requise pour hisser un satellite sur une orbite terrestre basse (le changement d'énergie potentielle) ne représente qu'une petite fraction de l'énergie cinétique nécessaire pour le maintenir en orbite. Est-ce vrai pour les orbites plus grandes ? Y a-t-il une tendance du rapport entre l'énergie cinétique et la variation de l'énergie potentielle à mesure que la taille de l'orbite augmente ?

13.4 Orbites et énergie des satellites

6. Un étudiant soutient qu'un satellite en orbite est en chute libre parce que le satellite continue de tomber vers la Terre. Un autre affirme qu'un satellite en orbite n'est pas en chute libre car l'accélération due à la gravité n'est pas de 9,80 m/s ². Avec qui êtes-vous d'accord et pourquoi ?
7. De nombreux satellites sont placés sur des orbites géosynchrones. Quelle est la particularité de ces orbites ? Pour un réseau de communication mondial, combien de ces satellites seraient nécessaires ?

13.5 Les lois de Kepler sur le mouvement planétaire

8. Les lois de Kepler sont-elles purement descriptives ou contiennent-elles des informations causales ?
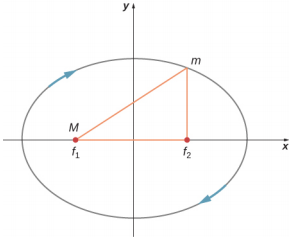
9. Dans le schéma ci-dessous, pour un satellite en orbite elliptique autour d'une masse beaucoup plus importante, indiquez où sa vitesse est la plus élevée et où elle est la plus faible. Quelle loi de conservation dicte ce comportement ? Indiquez les directions de la force, de l'accélération et de la vitesse à ces points. Tracez des vecteurs pour ces trois mêmes quantités aux deux points d'intersection de l'axe Y (le long de l'axe semi-mineur) et déterminez à partir de là si la vitesse augmente, diminue ou à une valeur max/min.

13.6 Forces marémotrices

10. Lorsqu'un objet tombe dans un trou noir, les forces de marée augmentent. Ces forces de marée déchireront-elles toujours l'objet lorsqu'il s'approche du rayon de Schwarzschild ? Comment la masse du trou noir et la taille de l'objet affectent-elles votre réponse ?

13.7 La théorie de la gravité d'Einstein

11. Le principe d'équivalence stipule que toutes les expériences effectuées en laboratoire dans un champ gravitationnel uniforme ne peuvent être distinguées de celles effectuées dans un laboratoire qui n'est pas dans un champ gravitationnel mais qui accélère de manière uniforme. Dans ce dernier cas, considérez ce qui arrive à un faisceau laser projeté à une certaine hauteur parfaitement horizontalement vers le sol, à travers le laboratoire d'accélération. (Visionnez ceci depuis une image qui n'accélère pas à l'extérieur du laboratoire.) Par rapport à la hauteur du laser, où le faisceau laser atteindra-t-il le mur le plus éloigné ? Qu'est-ce que cela indique à propos de l'effet d'un champ gravitationnel sur la lumière ? Le fait que la lumière n'ait pas de masse influence-t-il l'argument ?
12. Lorsqu'une personne s'approche du rayon de Schwarzschild d'un trou noir, des observateurs extérieurs voient tous les processus de cette personne (son horloge, son rythme cardiaque, etc.) ralentir et s'arrêter lorsqu'elle atteint le radius de Schwarzschild. (La personne qui tombe dans le trou noir voit ses propres processus intacts.) Mais la vitesse de la lumière est la même partout pour tous les observateurs. Qu'est-ce que cela signifie à propos de l'espace lorsque vous vous approchez du trou noir ?

Problèmes

13.1 La loi de Newton sur la gravitation universelle

13. Évaluez l'amplitude de la force gravitationnelle entre deux billes d'acier sphériques de 5 kg séparées par une distance centre à centre de 15 cm.
14. Estimez la force gravitationnelle entre deux lutteurs de sumo, pesant 220 kg et 240 kg, lorsqu'ils sont enlacés et que leurs centres sont distants de 1,2 m.
15. L'astrologie joue un rôle important dans la position des planètes au moment de la naissance. La seule force connue qu'une planète exerce sur la Terre est la force gravitationnelle. a) Calculez la force gravitationnelle exercée sur un bébé de 4,20 kg par un père de 100 kg situé à 0,200 m à la naissance (il aide, il est donc proche de l'enfant). (b) Calculez la force exercée sur le bébé par Jupiter s'il se trouve à la distance la plus proche de la Terre, à environ 6,29 x 10 ¹¹ m. Comment la force de Jupiter sur le bébé se compare-t-elle à la force du père sur le bébé ? D'autres objets présents dans la chambre et dans le bâtiment de l'hôpital exercent également des forces gravitationnelles similaires. (Bien entendu, une force inconnue peut agir, mais les scientifiques doivent d'abord être convaincus qu'il y a même un effet, et encore moins qu'une force inconnue en est la cause.)
16. Une montagne à 10,0 km d'une personne exerce sur celle-ci une force gravitationnelle égale à 2,00 % de son poids. (a) Calculez la masse de la montagne. (b) Comparez la masse de la montagne à celle de la Terre. (c) Qu'est-ce qui est déraisonnable dans ces résultats ? d) Quels sont les prémisses déraisonnables ou incohérentes ? (Notez que des mesures gravitationnelles précises peuvent facilement détecter l'effet des montagnes voisines et les variations de la géologie locale.)
17. La Station spatiale internationale a une masse d'environ 370 000 kg. a) Quelle est la force exercée sur une astronaute adaptée de 150 kg si elle se trouve à 20 m du centre de gravité de la station ? (b) Dans quelle mesure pensez-vous que votre réponse serait précise ?

Figure 13.33 (crédit : ©ESA — David Ducros)

18. L'astéroïde Toutatis est passé près de la Terre en 2006 à quatre fois la distance de notre Lune. C'est l'approche la plus proche que nous aurons jusqu'en 2060. S'il a une masse de 5,0 x 10 ¹³ kg, quelle force a-t-il exercée sur la Terre à son approche la plus proche ?
19. a) Quelle a été l'accélération de la Terre provoquée par l'astéroïde Toutatis (voir problème précédent) à son approche la plus proche ? (b) Quelle a été l'accélération de Toutatis à ce stade ?

13.2 Gravitation près de la surface de la Terre

20. a) Calculer la masse de la Terre étant donné que l'accélération due à la gravité au pôle Nord est mesurée à 9,832 m/s ² et que le rayon de la Terre au pôle est de 6 356 km. (b) Comparez cela avec la valeur de la fiche d'information sur la Terre de la NASA de 5,9726 x 10 ²⁴ kg.
21. (a) Quelle est l'accélération due à la gravité à la surface de la Lune ? (b) À la surface de Mars ? La masse de Mars est de 6,418 x 10 ²³ kg et son rayon est de 3,38 x 10 ⁶ m.
22. (a) Calculez l'accélération due à la gravité à la surface du Soleil. (b) De quel facteur votre poids augmenterait-il si vous pouviez vous tenir debout sur le soleil ? (Peu importe que tu ne le puisses pas.)
23. La masse d'une particule est de 15 kg. a) Quel est son poids sur Terre ? (b) Quel est son poids sur la Lune ? (c) Quelle est sa masse sur la Lune ? d) Quel est son poids dans l'espace extra-atmosphérique, loin de tout corps céleste ? e) Quelle est sa masse à ce stade ?
24. Sur une planète dont le rayon est de 1,2 x 10 ⁷ m, l'accélération due à la gravité est de 18 m/s ². Quelle est la masse de la planète ?
25. Le diamètre moyen de la planète Saturne est de 1,2 x 10 ⁸ m et sa densité de masse moyenne est de 0,69 g/cm ³. Déterminez l'accélération due à la gravité à la surface de Saturne.
26. Le diamètre moyen de la planète Mercure est de 4,88 x 10 ⁶ m et l'accélération due à la gravité à sa surface est de 3,78 m/s ². Estimez la masse de cette planète.
27. L'accélération due à la gravité à la surface d'une planète est trois fois plus importante qu'elle ne l'est à la surface de la Terre. La densité de masse de la planète est connue pour être le double de celle de la Terre. Quel est le rayon de cette planète par rapport au rayon de la Terre ?
28. Un corps à la surface d'une planète ayant le même rayon que celui de la Terre pèse 10 fois plus que sur Terre. Quelle est la masse de cette planète par rapport à la masse de la Terre ?

13.3 Énergie potentielle gravitationnelle et énergie totale

29. Déterminez la vitesse de fuite d'un projectile depuis la surface de Mars.
30. Détermine la vitesse de fuite d'un projectile depuis la surface de Jupiter.
31. Quelle est la vitesse d'échappement d'un satellite situé sur l'orbite de la Lune autour de la Terre ? Supposons que la Lune ne soit pas proche.
32. a) Évaluer l'énergie potentielle gravitationnelle entre deux billes d'acier sphériques de 5 kg séparées par une distance centre à centre de 15 cm. (b) En supposant qu'ils soient tous deux au repos l'un par rapport à l'autre dans l'espace lointain, utilisez les économies d'énergie pour déterminer à quelle vitesse ils se déplaceront au moment de l'impact. Chaque sphère a un rayon de 5,10 cm.
33. Un astéroïde de taille moyenne situé à 5,0 x 10 à ⁷ km de la Terre et d'une masse de 2,0 x 10 ¹³ kg est détecté et se dirige directement vers la Terre à une vitesse de 2,0 km/s. Quelle sera sa vitesse juste avant qu'il n'atteigne notre atmosphère ? (Vous pouvez ignorer la taille de l'astéroïde.)
34. (a) Quelle sera l'énergie cinétique de l'astéroïde lors du problème précédent juste avant qu'il n'atteigne la Terre ? b) Comparez cette énergie à la sortie de la plus grosse bombe à fission, 2100 TJ. Quel impact cela aurait-il sur la Terre ?
35. a) Quel est le changement d'énergie d'une charge utile de 1 000 kg prélevée au repos à la surface de la Terre et placée au repos à la surface de la Lune ? (b) Quelle serait la réponse si la charge utile était transportée de la surface de la Lune vers la Terre ? S'agit-il d'un calcul raisonnable de l'énergie nécessaire pour déplacer une charge utile d'avant en arrière ?

13.4 Orbites et énergie des satellites

36. Si une planète dont la masse est 1,5 fois supérieure à celle de la Terre se déplaçait sur l'orbite de la Terre, quelle serait sa période ?
37. Deux planètes sur des orbites circulaires autour d'une étoile ont des vitesses de v et de 2v. a) Quel est le rapport des rayons orbitaux des planètes ? (b) Quel est le ratio de leurs règles ?
38. En utilisant la distance moyenne entre la Terre et le Soleil et la période orbitale de la Terre, (a) déterminez l'accélération centripète de la Terre dans son mouvement autour du Soleil. (b) Comparez cette valeur à celle de l'accélération centripète à l'équateur due à la rotation de la Terre.
39. Quel est le rayon orbital d'un satellite de la Terre ayant une période de 1 heure ? (b) Qu'est-ce qui est déraisonnable dans ce résultat ?
40. Calculez la masse du Soleil sur la base des données de l'orbite de la Terre et comparez la valeur obtenue avec la masse réelle du Soleil.
41. Déterminez la masse de Jupiter en vous basant sur le fait que Io, sa lune la plus interne, a un rayon orbital moyen de 421 700 km et une période de 1,77 jour.
42. Les observations astronomiques de notre galaxie de la Voie lactée indiquent qu'elle a une masse d'environ 8,0 x 10 ¹¹ masses solaires. Une étoile orbitant à la périphérie de la galaxie se trouve à environ 6,0 x 10 à ⁴ années-lumière de son centre. (a) Quelle devrait être la période orbitale de cette étoile ? (b) Si sa période est plutôt de 6,0 x 10 ⁷ ans, quelle est la masse de la galaxie ? De tels calculs sont utilisés pour suggérer l'existence d'autres matières, comme un trou noir très massif au centre de la Voie lactée.
43. a) Afin d'empêcher un petit satellite de dériver vers un astéroïde voisin, il est placé sur orbite pendant une période de 3,02 heures et dans un rayon de 2,0 km. Quelle est la masse de l'astéroïde ? (b) Cette masse semble-t-elle raisonnable compte tenu de la taille de l'orbite ?
44. La Lune et la Terre tournent autour de leur centre de masse commun, situé à environ 4700 km du centre de la Terre. (C'est à 1690 km sous la surface.) (a) Calculez l'accélération due à la gravité de la Lune à ce point. (b) Calculez l'accélération centripète du centre de la Terre lorsqu'il tourne autour de ce point une fois par mois lunaire (environ 27,3 jours) et comparez-la à l'accélération trouvée dans la partie (a). Indiquez s'ils sont égaux ou non et pourquoi ils devraient ou ne devraient pas l'être.
45. Le Soleil tourne autour de la galaxie de la Voie lactée une fois tous les 2,60 x 10 ⁸ ans, avec une orbite à peu près circulaire dont le rayon moyen est de 3,00 x 10 ⁴ années-lumière. (Une année-lumière est la distance parcourue par la lumière en 1 an.) Calculez l'accélération centripète du Soleil sur son orbite galactique. Votre résultat confirme-t-il l'hypothèse selon laquelle un cadre de référence quasi inertiel peut être localisé au niveau du Soleil ? (b) Calculez la vitesse moyenne du Soleil sur son orbite galactique. La réponse vous surprend ?
46. Un satellite terrestre géosynchrone est un satellite dont la période orbitale est exactement d'un jour. Ces orbites sont utiles pour les communications et l'observation météorologique car le satellite reste au-dessus du même point de la Terre (à condition qu'il orbite dans le plan équatorial dans la même direction que la rotation de la Terre). Calculez le rayon d'une telle orbite en fonction des données pour la Terre présentées à l'annexe D.

13.5 Les lois de Kepler sur le mouvement planétaire

47. Calculez la masse du Soleil sur la base des données relatives à l'orbite moyenne de la Terre et comparez la valeur obtenue avec la valeur communément répertoriée du Soleil de 1,989 x 10 ³⁰ kg.
48. Io tourne autour de Jupiter avec un rayon moyen de 421 700 km et une période de 1 769 jours. Sur la base de ces données, quelle est la masse de Jupiter ?
49. Le rayon orbital « moyen » indiqué pour les objets astronomiques en orbite autour du Soleil n'est généralement pas une moyenne intégrée, mais il est calculé de telle sorte qu'il donne la période correcte lorsqu'il est appliqué à l'équation pour les orbites circulaires. Dans ces conditions, quel est le rayon orbital moyen en termes d'aphélie et de périhélie ?
50. Le périhélie de la comète de Halley est de 0,586 UA et celui de l'aphélie de 17,8 UA. Étant donné que sa vitesse au périhélie est de 55 km/s, quelle est la vitesse à l'aphélie (1 UA = 1,496 x 10 ¹¹ m) ? (Conseil : vous pouvez utiliser la conservation de l'énergie ou le moment cinétique, mais cette dernière option est beaucoup plus simple.)
51. Le périhélie de la comète Lagerkvist est de 2,61 UA et sa période est de 7,36 ans. Montrez que l'aphélie de cette comète est de 4,95 UA.
52. Quel est le rapport entre la vitesse au périhélie et celle à l'aphélie pour la comète Lagerkvist dans le problème précédent ?
53. Eros a une orbite elliptique autour du Soleil, avec une distance périhéliale de 1,13 UA et une distance d'aphélie de 1,78 UA. Quelle est la période de son orbite ?

13.6 Forces marémotrices

54. (a) Quelle est la différence entre les forces exercées sur une masse de 1,0 kg sur le côté proche d'Io et sur le côté éloigné dues à Jupiter ? Io a un rayon moyen de 1821 km et un rayon orbital moyen autour de Jupiter de 421 700 km. (b) Comparez cette différence à celle calculée pour la différence pour la Terre due à la Lune calculée dans l'exemple 13.14. Les forces des marées sont à l'origine de l'activité volcanique d'Io.
55. Si le Soleil s'effondrait dans un trou noir, le point de non-retour pour un chercheur se trouverait à environ 3 km de la singularité centrale. L'enquêteur serait-il capable de survivre en se rendant ne serait-ce qu'à 300 km du centre ? Répondez à cette question en déterminant la différence d'attraction gravitationnelle que les trous noirs exercent sur une masse de 1,0 kg à la tête et aux pieds de l'investigateur.
56. Reportez-vous à la Figure 13.23 dans Forces de marée. Ce diagramme représente les forces de marée des marées printanières. Esquissez un diagramme similaire pour les marées basses. (Conseil : par souci de simplicité, imaginez que le soleil et la lune contribuent de manière égale. Votre diagramme serait la somme vectorielle de deux champs de force (comme dans la Figure 13.23), réduite d'un facteur deux et superposée à angle droit.)

13.7 La théorie de la gravité d'Einstein

57. Quel est le rayon de Schwarzschild pour le trou noir au centre de notre galaxie s'il a une masse de 4 millions de masses solaires ?
58. Quel serait le rayon de Schwarzschild, à des années-lumière, si notre galaxie de 100 milliards d'étoiles de la Voie lactée s'effondrait dans un trou noir ? Comparez cela à notre distance du centre, soit environ 13 000 années-lumière.

Problèmes supplémentaires

59. Une étoile à neutrons est une étoile froide qui s'est effondrée et possède une densité nucléaire. Une étoile à neutrons particulière a une masse deux fois supérieure à celle de notre Soleil avec un rayon de 12,0 km. a) Quel serait le poids d'un astronaute de 100 kg debout à sa surface ? (b) Qu'est-ce que cela nous apprend sur l'atterrissage sur une étoile à neutrons ?
60. a) À quelle distance du centre de la Terre la force gravitationnelle nette de la Terre et de la Lune sur un objet serait-elle nulle ? (b) Le fait de régler les amplitudes des forces sur un pied d'égalité devrait donner deux réponses à partir du quadratique. Comprenez-vous pourquoi il y a deux positions, mais une seule où la force nette est nulle ?
61. À quelle distance du centre du Soleil la force gravitationnelle nette de la Terre et du Soleil sur un vaisseau spatial serait-elle nulle ?
62. Calculez les valeurs de g à la surface de la Terre pour les modifications suivantes des propriétés de la Terre : (a) sa masse est doublée et son rayon réduit de moitié ; (b) sa densité de masse est doublée et son rayon est inchangé ; (c) sa densité de masse est réduite de moitié et sa masse est inchangée.
63. Supposons que vous puissiez communiquer avec les habitants d'une planète d'un autre système solaire. Ils vous disent que sur leur planète, dont le diamètre et la masse sont respectivement de 5,0 x 10 ³ km et 3,6 x 10 ²³ kg, le record du saut en hauteur est de 2,0 m. Étant donné que ce record se situe à près de 2,4 m sur Terre, que pensez-vous de la capacité de saut de vos amis extraterrestres ?
64. (a) Supposons que votre poids mesuré à l'équateur soit égal à la moitié de votre poids mesuré au pôle d'une planète dont la masse et le diamètre sont égaux à ceux de la Terre. Quelle est la période de rotation de la planète ? (b) Auriez-vous besoin de prendre en compte la forme de cette planète ?
65. Un corps de 100 kg est pesé au pôle Nord et à l'équateur à l'aide d'une balance à ressort. Quel est le résultat de l'échelle à ces deux points ? Supposons que g = 9,83 m/s ² au pôle.
66. Trouvez la vitesse nécessaire pour échapper au système solaire en commençant par la surface de la Terre. Supposons qu'aucun autre corps ne soit impliqué et ne tenez pas compte du fait que la Terre se déplace sur son orbite. [Conseil : L'équation 13.6 ne s'applique pas. Utilisez l'équation 13.5 et incluez l'énergie potentielle de la Terre et du Soleil.
67. Examinons le problème précédent et incluez le fait que la vitesse orbitale de la Terre autour du Soleil est de 29,8 km/ s. a) Quelle vitesse par rapport à la Terre serait nécessaire et dans quelle direction devriez-vous quitter la Terre ? (b) Quelle sera la forme de la trajectoire ?
68. Une comète est observée à 1,50 UA du Soleil à une vitesse de 24,3 km/s. Cette comète se trouve-t-elle sur une orbite liée ou non ?
69. Un astéroïde a une vitesse de 15,5 km/s lorsqu'il se trouve à 2 UA du soleil. À son approche la plus proche, il se trouve à 0,400 UA du Soleil. Quelle est sa vitesse à ce moment-là ?
70. Les débris spatiaux laissés par les anciens satellites et leurs lanceurs constituent un danger pour les autres satellites. a) Calculer la vitesse d'un satellite sur une orbite située à 900 km au-dessus de la surface de la Terre. (b) Supposons qu'un rivet lâche se trouve sur une orbite du même rayon qui coupe l'orbite du satellite à un angle de 90°. Quelle est la vitesse du rivet par rapport au satellite juste avant de le frapper ? (c) Si sa masse est de 0,500 g et qu'il s'immobilise à l'intérieur du satellite, quelle quantité d'énergie en joules est générée par la collision ? (Supposons que la vitesse du satellite ne change pas de façon appréciable, car sa masse est bien supérieure à celle du rivet.)
71. Un satellite d'une masse de 1000 kg est en orbite circulaire autour de la Terre. Le rayon de l'orbite du satellite est égal à deux fois le rayon de la Terre. a) À quelle distance se trouve le satellite ? (b) Déterminer les énergies cinétique, potentielle et totale du satellite.
72. Après la promotion de Cérès au rang de planète naine, nous reconnaissons maintenant que le plus gros astéroïde connu est Vesta, avec une masse de 2,67 x 10 ²⁰ kg et un diamètre allant de 578 km à 458 km. En supposant que Vesta est sphérique avec un rayon de 520 km, déterminez la vitesse d'échappement approximative de sa surface.
73. a) Sur la base des données du problème précédent concernant l'astéroïde Vesta, quelle serait la période orbitale d'une sonde spatiale placée sur une orbite circulaire à 10 km de sa surface ? (b) Pourquoi ce calcul est-il au mieux d'une utilité marginale ?
74. Quelle est la vitesse orbitale de notre système solaire par rapport au centre de la Voie lactée ? Supposons que la masse à l'intérieur d'une sphère dont le rayon est égal à notre distance du centre est d'environ 100 milliards de masses solaires. Notre distance du centre est de 27 000 années-lumière.
75. (a) En utilisant les informations du problème précédent, de quelle vitesse avez-vous besoin pour échapper à la Voie lactée de notre position actuelle ? (b) Auriez-vous besoin d'accélérer un vaisseau spatial à cette vitesse par rapport à la Terre ?
76. Les orbites circulaires dans l'équation 13.10 pour les sections coniques doivent avoir une excentricité nulle. À partir de là, et en utilisant la deuxième loi de Newton appliquée à l'accélération centripète, montrez que la valeur de α dans l'équation 13.10 est donnée par\(\alpha = \frac{L^{2}}{GMm^{2}}\) où L est le moment cinétique du corps en orbite. La valeur de α est constante et donnée par cette expression quel que soit le type d'orbite.
77. Montrez que pour une excentricité égale à 1 dans l'équation 13.10 pour les sections coniques, la trajectoire est une parabole. Pour ce faire, remplacez les coordonnées polaires r par des coordonnées cartésiennes, x et y\(\theta\), et en montrant qu'elle a la forme générale d'une parabole, x = ay ² + par + c.
78. En utilisant la technique présentée dans Satellite Orbits and Energy, montrez que deux masses m ₁ et m ₂ sur des orbites circulaires autour de leur centre de masse commun auront une énergie totale\(E = K + E = K_{1} + k_{2} - \frac{Gm_{1} m_{2}}{r} = - \frac{G m_{1} m_{2}}{2r}\). Nous avons montré l'énergie cinétique des deux masses de manière explicite. (Conseil : Les masses orbitent aux rayons r ₁ et r ₂, respectivement, où r = r ₁ + r ₂. Veillez à ne pas confondre le rayon nécessaire à l'accélération centripète avec celui de la force gravitationnelle.)
79. Compte tenu de la distance du périhélie, p, et de la distance de l'aphélie, q, pour une orbite elliptique, montrent que la vitesse au périhélie, v _p, est donnée par\(v_{p} = \sqrt{\frac{2GM_{Sun}}{(q + p)} \frac{q}{p}}\). (Conseil : utilisez la conservation du moment cinétique pour relier v _p et v _q, puis remplacez-la dans l'équation de conservation de l'énergie.)
80. La comète P/1999 R1 possède un périhélie de 0,0570 UA et un aphélie de 4,99 UA. En utilisant les résultats du problème précédent, trouvez sa vitesse à aphélie. (Conseil : l'expression désigne le périhélie. Utilisez la symétrie pour réécrire l'expression de l'aphélie.)

Problèmes liés au défi

81. Un tunnel est creusé au centre d'une planète parfaitement sphérique et sans air de rayon R. En utilisant l'expression de g dérivée dans Gravitation Near Earth's Surface pour une densité uniforme, montrez qu'une particule de masse m tombée dans le tunnel exécutera un mouvement harmonique simple. Déduisez la période d'oscillation de m et montrez qu'elle a la même période qu'une orbite à la surface.
82. En suivant la technique utilisée dans Gravitation près de la surface de la Terre, déterminez la valeur de g en fonction du rayon r à partir du centre d'une planète à coque sphérique de densité constante\(\rho\) avec des rayons intérieur et extérieur R _entrant et R _sortant. Trouvez g pour R _dans < r < R en _sortie et pour r < R _dans. En supposant que l'intérieur de la coque est maintenu sans air, décrivez votre voyage à l'intérieur de la planète à coque sphérique.
83. Montrez que la vitesse surfacique pour une orbite circulaire de rayon r autour d'une masse M est de\(\frac{\Delta A}{\Delta t} = \frac{1}{2} \sqrt{GMr}\). Votre expression donne-t-elle la valeur correcte de la vitesse surfacique de la Terre autour du Soleil ?
84. Montrez que la période d'orbite de deux masses, m ₁ et m ₂, sur des orbites circulaires de rayons r ₁ et r ₂, respectivement, autour de leur centre de masse commun, est donnée par la formule\(T = 2 \pi \sqrt{\frac{r^{3}}{G(m_{1} + m_{2})}}\) où r = r ₁ + r ₂. (Conseil : Les masses orbitent aux rayons r ₁ et r ₂, respectivement où r = r ₁ + r ₂. Utilisez l'expression du centre de masse pour relier les deux rayons et notez que les deux masses doivent avoir des moments égaux mais opposés. Commencez par la relation entre la période et la circonférence et la vitesse de l'orbite pour l'une des masses. Utilisez le résultat du problème précédent en utilisant les moments dans les expressions de l'énergie cinétique.)
85. Montrez que pour de petites variations de hauteur h, telles que h << R _E, l'équation 13.4 se réduit à l'expression\(\Delta\) U = mgh.
86. À l'aide de la Figure 13.9, esquissez soigneusement un diagramme de corps libre pour le cas d'un simple pendule suspendu à la latitude lambda, en étiquetant toutes les forces agissant sur la masse ponctuelle, m. Définissez les équations du mouvement pour l'équilibre, en définissant une coordonnée dans la direction de l'accélération centripète (vers P sur le schéma), l'autre perpendiculaire à cela. Montrez que l'angle de déflexion\(\epsilon\), défini comme l'angle entre la chaîne du pendule et la direction radiale vers le centre de la Terre, est donné par l'expression ci-dessous. Quel est l'angle de déflexion à 45 degrés de latitude ? Supposons que la Terre soit une sphère parfaite. \(\tan(\lambda + \epsilon) = \frac{g}{(g − \omega^{2} R_{E})} \tan \lambda\), où\(\omega\) est la vitesse angulaire de la Terre.
87. (a) Montrer que la force de marée sur un petit objet de masse m, définie comme la différence entre la force gravitationnelle qui serait exercée sur m à une distance du côté proche et du côté éloigné de l'objet, en raison de la gravitation à une distance R de M, est donnée par F _tidal =\(\frac{2GMm}{R^{3}} \Delta\) r où \(\Delta\)r est la distance entre le côté proche et le côté éloigné et\(\Delta\) r << R. (b) Supposons que vous tombiez les pieds les premiers dans le trou noir au centre de notre galaxie. Il a une masse de 4 millions de masses solaires. Quelle serait la différence entre la force exercée sur votre tête et celle exercée sur vos pieds dans le rayon de Schwarzschild (horizon des événements) ? Supposons que vos pieds et votre tête ont chacun une masse de 5,0 kg et sont distants de 2,0 m. Surviendriez-vous à traverser l'horizon des événements ?
88. Trouvez les vitesses de transfert de Hohmann,\(\Delta\) v _EllipseEarth et\(\Delta\) v _EllipseMars, nécessaires pour un voyage vers Mars. Utilisez l'équation 13.7 pour déterminer les vitesses orbitales circulaires de la Terre et de Mars. À l'aide de l'équation 13.4 et de l'énergie totale de l'ellipse (avec le demi-grand axe a)\(\frac{GmM_{s}}{2a}\), donnée par E = −, déterminez les vitesses sur Terre (périhélie) et sur Mars (aphélie) requises pour se trouver sur l'ellipse de transfert. La différence,\(\Delta\) v, en chaque point est l'augmentation de vitesse ou la vitesse de transfert nécessaire.

Contributeurs et attributions

Template:ContribOpenStaxUni