12.5 : Contrainte, déformation et module d'élasticité (partie 2)

Contrainte globale, déformation et module

Lorsque vous plongez dans l'eau, vous sentez une force s'exercer sur chaque partie de votre corps, de toutes les directions. Ce que vous ressentez alors, c'est du stress global, ou en d'autres termes, de la pression. Les contraintes d'encombrement ont toujours tendance à réduire le volume enfermé par la surface d'un objet immergé. Les forces de cette « compression » sont toujours perpendiculaires à la surface immergée Figure\(\PageIndex{1}\). Ces forces ont pour effet de diminuer le volume de l'objet immergé d'une quantité\(\Delta\) V par rapport au volume V ₀ de l'objet en l'absence de contrainte d'encombrement. Ce type de déformation est appelé déformation globale et se décrit par un changement de volume par rapport au volume d'origine :

\[bulk\; strain = \frac{\Delta V}{V_{0}} \label{12.37}\]

Figure\(\PageIndex{1}\) : Un objet soumis à une contrainte d'encombrement croissante subit toujours une diminution de son volume. Des forces égales perpendiculaires à la surface agissent dans toutes les directions. Ces forces ont pour effet de diminuer le volume de la quantité\(\Delta\) V par rapport au volume d'origine, V ₀.

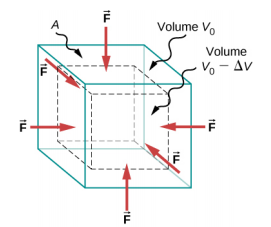
La contrainte d'encombrement résulte de la contrainte d'encombrement, qui est une force F _\(\perp\)normale à une surface qui exerce une pression sur la surface unitaire A d'un objet immergé. Ce type de quantité physique, ou pression p, est défini comme

\[pressure = p \equiv \frac{F_{\perp}}{A} \ldotp \label{12.38}\]

Nous étudierons la pression dans les fluides plus en détail dans la section Mécanique des fluides. Une caractéristique importante de la pression est qu'il s'agit d'une quantité scalaire qui n'a pas de direction particulière ; c'est-à-dire que la pression agit de manière égale dans toutes les directions possibles. Lorsque vous plongez votre main dans l'eau, vous ressentez la même pression s'exerçant sur la surface supérieure de votre main que sur la surface inférieure, ou sur la surface latérale ou sur la surface de la peau entre vos doigts. Ce que vous percevez dans ce cas, c'est une augmentation de la pression\(\Delta\) p par rapport à ce que vous avez l'habitude de ressentir lorsque votre main n'est pas immergée dans l'eau. Ce que vous ressentez lorsque votre main n'est pas immergée dans l'eau est la pression normale p ₀ d'une atmosphère, qui sert de point de référence. La contrainte globale est cette augmentation de pression, ou\(\Delta\) p, par rapport au niveau normal, p ₀.

Lorsque la contrainte d'encombrement augmente, la déformation globale augmente en réponse, conformément à l'équation 12.4.4. La constante de proportionnalité dans cette relation est appelée module global, B, ou

\[B = \frac{bulk\; stress}{bulk\; strain} = \frac{\Delta p}{\frac{\Delta V}{V_{0}}} = - \Delta p \frac{V_{0}}{\Delta V} \ldotp \label{12.39}\]

Le signe moins qui apparaît dans l'équation \ ref {12.39} sert à des fins de cohérence, afin de garantir qu'il s'\(B\)agit d'une quantité positive. Notez que le signe moins (—) est nécessaire car une augmentation\(\Delta\) p de la pression (une quantité positive) entraîne toujours une diminution\(\Delta\) V du volume, et une diminution du volume est une quantité négative. L'inverse du module global est appelé compressibilité k, ou

\[k = \frac{1}{B} = - \frac{\frac{\Delta V}{V_{0}}}{\Delta p} \ldotp \label{12.40}\]

Le terme « compressibilité » est utilisé en relation avec les fluides (gaz et liquides). La compressibilité décrit la variation du volume d'un fluide par unité d'augmentation de pression. Les fluides caractérisés par une forte compressibilité sont relativement faciles à comprimer. Par exemple, la compressibilité de l'eau est de 4,64 x 10 ^-5 /atm et la compressibilité de l'acétone est de 1,45 x 10 ^-4 /atm. Cela signifie que lorsque la pression augmente de 1,0 atm, la diminution relative du volume est environ trois fois plus importante pour l'acétone que pour l'eau.

Exemple\(\PageIndex{1}\): Hydraulic Press

Dans une presse hydraulique Figure\(\PageIndex{2}\), un volume d'huile de 250 litres est soumis à une augmentation de pression de 2 300 psi. Si la compressibilité de l'huile est de 2,0 x 10 ^-5/atm, déterminez la déformation apparente et la diminution absolue du volume d'huile lorsque la presse fonctionne.

Figure\(\PageIndex{2}\) : Dans une presse hydraulique, lorsqu'un petit piston est déplacé vers le bas, la pression de l'huile est transmise dans l'huile au gros piston, provoquant le déplacement du gros piston vers le haut. Une faible force appliquée à un petit piston provoque une force de pression importante, que le gros piston exerce sur un objet qui est soit soulevé, soit pressé. L'appareil agit comme un levier mécanique.

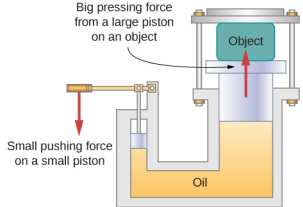
Stratégie

Nous devons inverser l'équation \ ref {12.40} pour trouver la déformation globale. Tout d'abord, nous convertissons l'augmentation de pression de psi en atm,\(\Delta\) p = 2300 psi =\(\frac{2300}{14.7\; atm}\) ≈ 160 atm, et identifions V ₀ = 250 L.

Solution

En substituant des valeurs dans l'équation, nous avons

\[bulk\; strain = \frac{\Delta V}{V_{0}} = \frac{\Delta p}{B} = k \Delta p = (2.0 \times 10^{-5}\; /atm)(160\; atm) = 0.0032\]

réponse

\[\Delta V = 0.0032 V_{0} = 0.0032 (250\; L) = 0.78\; L \ldotp\]

L'importance

Notez que, étant donné que la compressibilité de l'eau est 2,32 fois supérieure à celle de l'huile, si la substance active de la presse hydraulique présentant ce problème était remplacée par de l'eau, la déformation apparente ainsi que la variation de volume seraient 2,32 fois plus importantes.

Exercice\(\PageIndex{1}\)

Si la force normale agissant sur chaque face d'une pièce d'acier cubique de 1,0 m ³ est modifiée de 1,0 x 10 ⁷ N, déterminez la variation résultante du volume de la pièce d'acier.

Contrainte de cisaillement, déformation et module

Les concepts de contrainte de cisaillement et de déformation ne concernent que les objets solides ou les matériaux. Les bâtiments et les plaques tectoniques sont des exemples d'objets qui peuvent être soumis à des contraintes de cisaillement. En général, ces concepts ne s'appliquent pas aux fluides.

La déformation par cisaillement se produit lorsque deux forces antiparallèles d'égale amplitude sont appliquées tangentiellement à des surfaces opposées d'un objet solide, ne provoquant aucune déformation dans le sens transversal à la ligne de force, comme dans l'exemple typique de contrainte de cisaillement illustré à la figure\(\PageIndex{3}\). La déformation par cisaillement est caractérisée par un déplacement graduel\(\Delta\) x des couches dans la direction tangente aux forces d'action. Cette gradation en\(\Delta\) x se produit dans la direction transversale sur une certaine distance L ₀. La contrainte de cisaillement est définie par le rapport entre le plus grand déplacement\(\Delta\) x et la distance transversale L ₀

\[shear\; strain = \frac{\Delta x}{L_{0}} \ldotp \label{12.41}\]

La contrainte de cisaillement est causée par la contrainte de cisaillement. La contrainte de cisaillement est due à des forces qui agissent parallèlement à la surface. Nous utilisons le symbole F _{\(\parallel\)}pour ces forces. La magnitude F _{\(\parallel\)}par surface A à laquelle la force de cisaillement est appliquée est la mesure de la contrainte de cisaillement

\[shear\; stress = \frac{F_{\parallel}}{A} \ldotp \label{12.42}\]

Le module de cisaillement est la constante de proportionnalité dans l'équation \ ref {12.33} et est défini par le rapport contrainte/déformation. Le module de cisaillement est communément désigné par\(S\) :

\[S = \frac{shear\; stress}{shear\; strain} = \frac{\frac{F_{\parallel}}{A}}{\frac{\Delta x}{L_{0}}} = \frac{F_{\parallel}}{A} \frac{L_{0}}{\Delta x} \ldotp \label{12.43}\]

Figure\(\PageIndex{3}\) : Un objet soumis à une contrainte de cisaillement : deux forces antiparallèles d'égale amplitude sont appliquées tangentiellement aux surfaces parallèles opposées de l'objet. Le contour en pointillés représente la déformation résultante. Il n'y a pas de changement de direction transversale aux forces d'action et la longueur transversale L ₀ n'est pas affectée. La déformation par cisaillement est caractérisée par un déplacement graduel\(\Delta\) x des couches dans la direction tangente aux forces.

Exemple\(\PageIndex{2}\): An Old Bookshelf

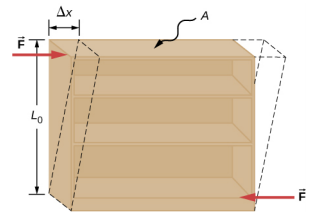
Une personne de ménage essaie de déplacer une vieille bibliothèque lourde sur un sol recouvert de moquette en appuyant tangentiellement sur la surface de l'étagère supérieure. Cependant, le seul effet perceptible de cet effort est similaire à celui observé sur la figure\(\PageIndex{2}\), et il disparaît lorsque la personne arrête de pousser. La bibliothèque mesure 180,0 cm de haut et 90,0 cm de large avec quatre étagères de 30,0 cm de profondeur, toutes partiellement chargées de livres. Le poids total de la bibliothèque et des livres est de 600,0 N. Si la personne pousse l'étagère supérieure d'une pression de 50,0 N qui déplace l'étagère supérieure horizontalement de 15 cm par rapport à l'étagère inférieure immobile, déterminez le module de cisaillement de la bibliothèque.

Stratégie

Les seules informations pertinentes sont les dimensions physiques de la bibliothèque, la valeur de la force tangentielle et le déplacement que cette force provoque. Nous identifions F _{\(\parallel\)}= 50,0 N,\(\Delta\) x = 15,0 cm, L ₀ = 180,0 cm et A = (30,0 cm) (90,0 cm) = 2700,0 cm ², et nous utilisons l'équation \ ref {12.43} pour calculer le module de cisaillement.

Solution

En substituant des nombres dans les équations, nous obtenons le module de cisaillement

\[S = \frac{F_{\parallel}}{A} \frac{L_{0}}{\Delta x} = \frac{50.0\; N}{2700.0\; cm^{2}} \frac{180.0\; cm}{15.0\; cm} = \frac{2}{9} \frac{M}{cm^{2}} = \frac{2}{9} \times 10^{4}\; N/m^{2} = \frac{20}{9} \times 10^{3}\; Pa = 2.222\; kPa \ldotp \nonumber\]

Nous pouvons également trouver la contrainte de cisaillement et la déformation, respectivement :

\[\frac{F_{\parallel}}{A} = \frac{50.0\; N}{2700.0\; cm^{2}} = \frac{5}{27}\; kPa = 185.2\; Pa \nonumber\]

\[\frac{\Delta x}{L_{0}} = \frac{15.0\; cm}{180.0\; cm} = \frac{1}{12} = 0.083 \ldotp \nonumber\]

L'importance

Si, dans cet exemple, la personne poussait l'étagère de façon saine, il se peut que la cisaille induite la réduise en un tas de déchets. À peu près le même mécanisme de cisaillement est responsable de la défaillance des barrages et des digues remplis de terre et, en général, des glissements de terrain.

Exercice\(\PageIndex{2}\)

Expliquez pourquoi les concepts de module de Young et de module de cisaillement ne s'appliquent pas aux fluides.