Skip to main content
Global

11.5 : Précession d'un gyroscope

  1. Last updated
  2. Save as PDF
  • Page ID
    191261

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objectifs d'apprentissage

    • Décrire les processus physiques qui sous-tendent le phénomène de précession
    • Calculez la vitesse angulaire de précession d'un gyroscope

    La figure\(\PageIndex{1}\) montre un gyroscope, défini comme un disque rotatif dans lequel l'axe de rotation est libre de prendre n'importe quelle orientation. Lors de la rotation, l'orientation de l'axe de rotation n'est pas affectée par l'orientation du corps qui l'entoure. La carrosserie ou le véhicule qui entoure le gyroscope peut être déplacé d'un endroit à l'autre et l'orientation de l'axe de rotation restera la même. Cela rend les gyroscopes très utiles pour la navigation, en particulier lorsque les compas magnétiques ne peuvent pas être utilisés, comme dans les engins spatiaux habités et non habités, les missiles balistiques intercontinentaux, les véhicules aériens sans pilote et les satellites tels que le télescope spatial Hubble.

    Dessin d'un gyroscope, composé d'un disque qui peut tourner sur un arbre, perpendiculairement au plan du disque et passant par son centre. Deux anneaux entourent le gyroscope. L'un est fixé à l'arbre au-dessus et en dessous du disque, et l'autre est fixé au premier anneau et se trouve dans le plan du disque de telle sorte que ce second anneau soit concentrique par rapport au disque.
    Figure\(\PageIndex{1}\) : Un gyroscope est constitué d'un disque rotatif autour d'un axe qui peut prendre n'importe quelle orientation.

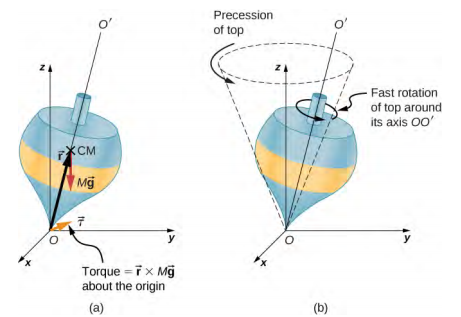
    Nous illustrons la précession d'un gyroscope avec un exemple de sommet dans les deux figures suivantes. Si le sommet est placé sur une surface plane proche de la surface de la Terre à un angle par rapport à la verticale et ne tourne pas, il tombera sous l'effet de la force de gravité produisant un couple agissant sur son centre de gravité. Ceci est illustré dans la figure\(\PageIndex{2a}\). Toutefois, si le sommet tourne sur son axe, plutôt que de se renverser sous l'effet de ce couple, il avance autour de la verticale, comme indiqué à la\(\PageIndex{2b}\). Cela est dû au couple sur le centre de masse, qui provoque le changement du moment cinétique.

    Figure a : Un système de coordonnées x y z est affiché, avec x hors de la page, y vers la droite et z vers le haut. L'origine est le point O. Un sommet est représenté avec son point à l'origine et son axe incliné à l'opposé de l'axe vertical z. L'axe du sommet est la ligne O O prime. Le vecteur r s'étend de l'origine au centre de la masse, marqué C M, du sommet. La force M g agit vers le bas au centre de masse. Le couple autour de l'origine est égal au vecteur r croisé avec le vecteur M. g. Ce couple est un vecteur dans le plan x y, perpendiculaire au vecteur r. Figure b : La coordonnée x y z et la partie supérieure sont affichées. Le sommet est à nouveau incliné par rapport à l'axe z et tourne rapidement dans le sens antihoraire autour de l'axe principal O O, vu de dessus. La précession du sommet trace un cercle dans le sens antihoraire vu de dessus, centré sur l'axe z. Le cône balayé par la précession du sommet est indiqué par des lignes pointillées.
    Figure\(\PageIndex{2}\) : (a) Si le sommet ne tourne pas, c'est qu'il y a un couple\(\vec{r} \times M\vec{g}\) autour de l'origine et que le sommet tombe. (b) Si le sommet tourne autour de son axe OO′, il ne tombe pas mais avance autour de l'axe Z.

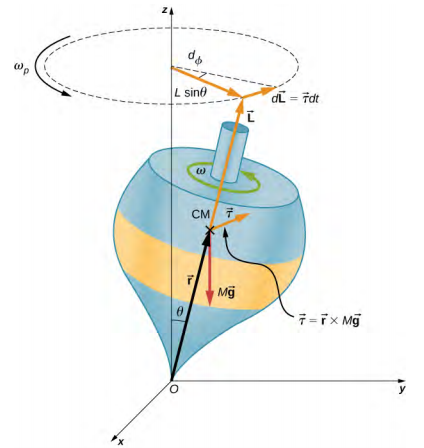
    La figure\(\PageIndex{3}\) montre les forces agissant sur une toupie. Le couple produit est perpendiculaire au vecteur de moment cinétique. Cela modifie la direction du vecteur de moment cinétique\(\vec{L}\) en fonction de d\(\vec{L}\) =\(\vec{\tau}\) dt, mais pas de sa magnitude. Le sommet se situe autour d'un axe vertical, car le couple est toujours horizontal et perpendiculaire à\(\vec{L}\). Si le sommet ne tourne pas, il acquiert un moment cinétique dans le sens du couple et tourne autour d'un axe horizontal, tombant comme prévu.

    Un système de coordonnées x y z est affiché, avec x hors de la page, y vers la droite et z vers le haut. L'origine est le point O. Un sommet est représenté avec son point à l'origine et son axe incliné d'un angle thêta par rapport à l'axe vertical z, dans le sens des aiguilles d'une montre lorsque nous le voyons. Le vecteur r s'étend de l'origine au centre de la masse, marqué C M, du sommet. La force M g agit vers le bas au centre de masse. Le couple, tau, autour de l'origine est égal au vecteur r croisé avec le vecteur M. g. Ce couple est un vecteur dans le plan x y, perpendiculaire au vecteur r, dans la page. La vitesse angulaire, oméga, du sommet est dans le sens antihoraire vu de dessus. Le moment cinétique, L, est dans la même direction que le vecteur r, incliné vers le haut le long de l'axe du sommet. Le cercle tracé par la précession du sommet est représenté par un cercle horizontal au-dessus du sommet. La vitesse angulaire de précession omega sub p est dans le sens antihoraire, vue de dessus. Le rayon du cercle de précession est L sinus thêta. Le vecteur d L est tangent au cercle, pointant vers la page, et est égal au vecteur tau d t. Le triangle formé L sinus thêta et d L est représenté, et l'angle opposé à d L est marqué par d phi.
    Figure\(\PageIndex{3}\) : La force de gravité agissant sur le centre de gravité produit un couple\(\vec{\tau}\) dans la direction perpendiculaire à\(\vec{L}\). L'amplitude de\(\vec{L}\) ne change pas, mais sa direction change, et la partie supérieure est précisée par rapport à l'axe Z.

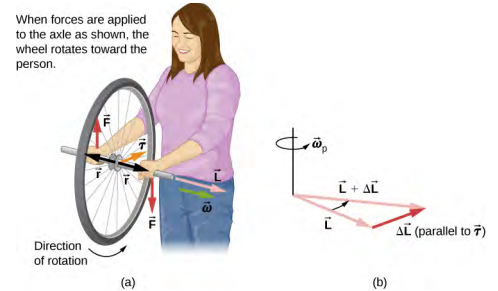
    Nous pouvons constater ce phénomène de première main en tenant une roue de vélo qui tourne et en essayant de la faire pivoter autour d'un axe perpendiculaire à l'axe de rotation. Comme le montre la figure\(\PageIndex{4}\), la personne applique des forces perpendiculaires à l'axe de rotation pour tenter de faire tourner la roue, mais l'axe de la roue commence à changer de direction vers la gauche en raison du couple appliqué.

    Sur la figure a, une femme, face au spectateur, tient une roue de vélo qui tourne de rayon r par l'essieu. La roue est telle que la vitesse angulaire oméga et le moment cinétique L se situent le long de l'axe de rotation de la roue, à sa gauche (à la droite du spectateur). C'est-à-dire que le mouvement de la roue est tel que le bas de la roue se déplace vers elle (dans la page). La direction de la force F appliquée par sa main gauche est indiquée vers le bas et celle par sa main droite vers le haut. Le couple tau est dirigé vers elle (dans la page.) Sur la figure b, l'addition de deux vecteurs L et delta-L, qui est parallèle au couple tau, est illustrée. La résultante des deux vecteurs est étiquetée L plus delta L. Le sens de rotation, omega sub p, est dans le sens antihoraire vu de dessus.
    Figure\(\PageIndex{4}\) : (a) Une personne tenant la roue du vélo en rotation la soulève de la main droite et la pousse vers le bas avec sa main gauche pour tenter de faire tourner la roue. Cette action crée un couple directement vers elle. Ce couple provoque une modification du moment cinétique exactement\(\Delta \vec{L}\) dans la même direction. (b) Un diagramme vectoriel illustrant comment\(\Delta \vec{L}\) et\(\vec{L}\) additionner, produisant un nouveau moment cinétique pointant davantage vers la personne. La roue se déplace vers la personne, perpendiculairement aux forces qu'elle exerce sur elle.

    Nous savons tous à quel point il est facile pour un vélo de basculer lorsqu'il est assis dessus au repos. Mais lorsque l'on roule à un bon rythme, il est plus difficile de le renverser car il faut modifier le vecteur de moment cinétique des rouets.

    Remarque

    Regardez cette vidéo sur la précession du gyroscope pour une démonstration complète de la précession de la roue de vélo.

    De plus, lorsqu'un disque rotatif est placé dans une boîte telle qu'un lecteur Blu-Ray, essayez de le déplacer. Il est facile de déplacer la boîte dans une direction donnée mais difficile de la faire pivoter autour d'un axe perpendiculaire à l'axe du disque rotatif, car nous appliquons un couple sur la boîte qui provoquera la précession du vecteur de moment cinétique du disque rotatif.

    Nous pouvons calculer le taux de précession du sommet sur la figure\(\PageIndex{3}\). Sur la figure\(\PageIndex{3}\), nous voyons que l'amplitude du couple est

    \[\tau = rMg \sin \theta \ldotp\]

    Ainsi,

    \[dL = rMg \sin \theta dt \ldotp\]

    L'angle que passe le sommet dans le temps dt est

    \[d \phi = \frac{dL}{L \sin \theta} = \frac{rMg \sin \theta}{L \sin \theta} dt = \frac{rMg}{L} dt \ldotp\]

    La vitesse angulaire de précession est\(\omega_{P} = \frac{d \phi}{dt}\) et, à partir de cette équation, nous voyons que

    \[\omega_{P} = \frac{rMg}{L} \ldotp\]

    ou, puisque L = I\(\omega\),

    \[\omega_{P} = \frac{rMg}{I \omega} \ldotp \label{11.12}\]

    Dans cette dérivation, nous avons supposé que\(\omega_{P}\) <<\(\omega\), c'est-à-dire que la vitesse angulaire de précession est bien inférieure à la vitesse angulaire du disque du gyroscope. La vitesse angulaire de précession ajoute une petite composante au moment cinétique le long de l'axe Z. Cela se voit par un léger mouvement de haut en bas à mesure que le gyroscope avance, appelé nutation.

    La Terre elle-même agit comme un gigantesque gyroscope. Son moment cinétique se trouve le long de son axe et pointe actuellement vers Polaris, l'étoile polaire. Mais la Terre avance lentement (une fois tous les 26 000 ans environ) en raison du couple du Soleil et de la Lune sur sa forme non sphérique.

    Exemple\(\PageIndex{1}\): Period of Precession

    Un gyroscope tourne avec son extrémité au sol et tourne avec une résistance au frottement négligeable. Le disque du gyroscope a une masse de 0,3 kg et tourne à 20 tr/min. Son centre de gravité se trouve à 5,0 cm du pivot et le rayon du disque est de 5,0 cm. Quelle est la période de précession du gyroscope ?

    Stratégie

    Nous utilisons l'équation \ ref {11.12} pour déterminer la vitesse angulaire précessionnelle du gyroscope. Cela nous permet de trouver la période de précession.

    Solution

    Le moment d'inertie du disque est

    \[I = \frac{1}{2} mr^{2} = \frac{1}{2} (0.30\; kg)(0.05\; m)^{2} = 3.75 \times 10^{-4}\; kg\; \cdotp m^{2} \ldotp \nonumber\]

    La vitesse angulaire du disque est

    \[20.0\; rev/s = (20.0)(2 \pi)\; rad/s = 125.66\; rad/s \ldotp \nonumber\]

    Nous pouvons maintenant le remplacer dans l'équation \ ref {11.12}. La vitesse angulaire précessionnelle est

    \[\omega_{P} = \frac{rMg}{I \omega} = \frac{(0.05\; m)(0.3\; kg)(9.8\; m/s^{2})}{(3.75 \times 10^{-4}\; kg\; \cdotp m^{2})(125.66\; rad/s)} = 3.12\; rad/s \ldotp \nonumber\]

    La période de précession du gyroscope est

    \[T_{P} = \frac{2 \pi}{3.12\; rad/s} = 2.0\; s \ldotp \nonumber\]

    L'importance

    La fréquence angulaire de précession du gyroscope, 3,12 rad/s, soit environ 0,5 tr/min, est bien inférieure à la vitesse angulaire de 20 tr/min du disque du gyroscope. Par conséquent, nous ne nous attendons pas à ce qu'une grande partie du moment cinétique soit due à la précession, et l'équation 11.12 est une bonne approximation de la vitesse angulaire de précession.

    Exercices\(\PageIndex{1}\)

    Un sommet a une fréquence de précession de 5,0 rad/s sur Terre. Quelle est sa fréquence de précession sur la Lune ?