11.4 : Conservation du moment cinétique
- Page ID
- 191274
- Appliquer la conservation du moment cinétique pour déterminer la vitesse angulaire d'un système rotatif dans lequel le moment d'inertie change
- Expliquer comment l'énergie cinétique de rotation change lorsqu'un système subit des changements de moment d'inertie et de vitesse angulaire
Jusqu'à présent, nous avons étudié le moment cinétique de systèmes composés de particules ponctuelles et de corps rigides. Nous avons également analysé les couples impliqués, en utilisant l'expression qui relie le couple net externe à la variation du moment cinétique. Des exemples de systèmes qui obéissent à cette équation incluent un pneu de vélo qui tourne librement et qui ralentit au fil du temps en raison du couple résultant de la friction, ou le ralentissement de la rotation de la Terre sur des millions d'années dû aux forces de friction exercées sur les déformations dues aux marées.
Supposons toutefois qu'il n'y ait pas de couple externe net sur le système,\(\sum \vec{\tau}\) = 0. Dans ce cas, nous pouvons introduire la loi de conservation du moment cinétique.
Le moment cinétique d'un système de particules autour d'un point dans un référentiel inertiel fixe est conservé s'il n'y a pas de couple externe net autour de ce point :
\[\frac{d \vec{L}}{dt} = 0 \label{11.10}\]
ou
\[\vec{L} = \vec{l}_{1} + \vec{l}_{2} + \cdots + \vec{l}_{N} = constant \ldotp \label{11.11}\]
Notez que le moment cinétique total\(\vec{L}\) est conservé. Tous les moments angulaires individuels peuvent changer tant que leur somme reste constante. Cette loi est analogue à la conservation du moment linéaire lorsque la force externe sur un système est nulle.
À titre d'exemple de conservation du moment cinétique, la figure\(\PageIndex{1}\) montre un patineur sur glace exécutant une vrille. Le couple net sur elle est très proche de zéro car il y a relativement peu de friction entre ses patins et la glace. De plus, le frottement s'exerce très près du point de pivot. Les deux\(|\vec{F}|\)\(|\vec{r}|\) sont petits,\(|\vec{\tau}|\) donc négligeables. Par conséquent, elle peut tourner pendant un certain temps. Elle peut également augmenter sa vitesse de rotation en tirant ses bras et ses jambes vers l'intérieur. Pourquoi le fait de tirer ses bras et ses jambes augmente-t-il sa vitesse de rotation ? La réponse est que son moment cinétique est constant, de sorte que
\[L' = L\]
ou
\[I' \omega' = I \omega,\]
où les quantités apprêtées se réfèrent à l'état de santé après qu'elle a tiré dans ses bras et réduit son moment d'inertie. Comme I' est plus petit, la vitesse angulaire\(\omega\) ′ doit augmenter pour maintenir le moment cinétique constant.
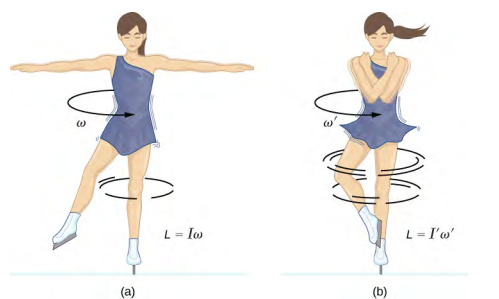
Il est intéressant de voir comment l'énergie cinétique de rotation de la patineuse change lorsqu'elle tire ses bras vers l'intérieur. Son énergie de rotation initiale est
\[K_{Rot} = \frac{1}{2} I \omega^{2},\]
alors que son énergie de rotation finale est
\[K'_{Rot} = \frac{1}{2} I (\omega')^{2} \ldotp\]
Puisque I′\(\omega\) ′ = I\(\omega\), on peut remplacer\(\omega\) ′ et trouver
\[K'_{Rot} = \frac{1}{2} I' (\omega')^{2} = \frac{1}{2} I' \left(\dfrac{I}{I'} \omega \right)^{2} = \frac{1}{2} I \omega^{2} \left(\dfrac{I}{I'}\right) = K_{Rot} \left(\dfrac{I}{I'}\right) \ldotp\]
Comme son moment d'inertie a diminué\(I′ < I\), son énergie cinétique de rotation finale a augmenté. La source de cette énergie cinétique de rotation supplémentaire est le travail requis pour tirer ses bras vers l'intérieur. Notez que les bras du patineur ne bougent pas dans un cercle parfait, ils spiralent vers l'intérieur. Ce travail provoque une augmentation de l'énergie cinétique de rotation, tandis que son moment cinétique reste constant. Comme elle se trouve dans un environnement sans friction, aucune énergie ne s'échappe du système. Ainsi, si elle tendait ses bras jusqu'à leur position initiale, elle tournerait à sa vitesse angulaire initiale et son énergie cinétique retrouverait sa valeur initiale.
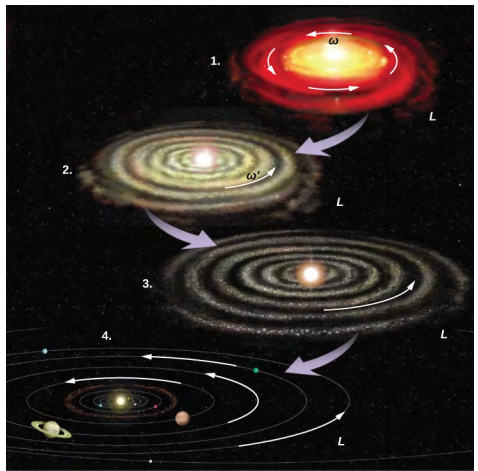
Le système solaire est un autre exemple du fonctionnement de la conservation du moment cinétique dans notre univers. Notre système solaire est né d'un énorme nuage de gaz et de poussière qui avait initialement une énergie de rotation. Les forces gravitationnelles ont provoqué la contraction du nuage et la vitesse de rotation a augmenté en raison de la conservation du moment cinétique (Figure\(\PageIndex{2}\)).
Nous poursuivons notre discussion avec un exemple qui a des applications en ingénierie.
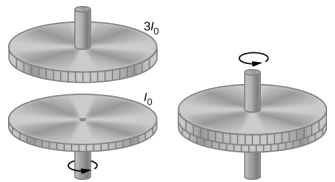
Un volant tourne sans friction à une vitesse angulaire\(\omega_{0}\) = 600 tr/min sur un arbre vertical sans friction avec une inertie de rotation négligeable. Un second volant, qui est au repos et possède un moment d'inertie trois fois supérieur à celui du volant rotatif, est déposé dessus (Figure\(\PageIndex{3}\)). En raison de la friction entre les surfaces, les volants atteignent très rapidement la même vitesse de rotation, après quoi ils tournent ensemble.
- Utilisez la loi de conservation du moment cinétique pour déterminer la vitesse angulaire\(\omega\) de la combinaison.
- Quelle fraction de l'énergie cinétique initiale est perdue lors de l'accouplement des volants ?
Stratégie
La partie (a) est simple à résoudre pour déterminer la vitesse angulaire du système couplé. Nous utilisons le résultat de (a) pour comparer les énergies cinétiques initiale et finale du système dans la partie (b).
Solution
- Aucun couple externe n'agit sur le système. La force due au frottement produit un couple interne qui n'affecte pas le moment cinétique du système. Par conséquent, la conservation du moment cinétique donne\[I_{0} \omega_{0} = (I_{0} + 3I_{0}) \omega, \nonumber\]\[\omega = \frac{1}{4} \omega_{0} = 150\; rev/min = 15.7\; rad/s \ldotp \nonumber\]
- Avant le contact, un seul volant tourne. L'énergie cinétique de rotation de ce volant est l'énergie cinétique de rotation initiale du système,\(\frac{1}{2} I_{0} \omega_{0}^{2}\). L'énergie cinétique finale est\[\frac{1}{2} (4I_{0}) \omega^{2} = \frac{1}{2} (4I_{0}) \left(\dfrac{\omega_{0}}{4}\right)^{2} = \frac{1}{8} I_{0} \omega_{0}^{2}. \nonumber\] Par conséquent, le rapport entre l'énergie cinétique finale et l'énergie cinétique initiale est\[\frac{\frac{1}{8} I_{0} \omega_{0}^{2}}{\frac{1}{2} I_{0} \omega_{0}^{2}} = \frac{1}{4} \ldotp \nonumber\] Ainsi, les 3/4 de l'énergie cinétique initiale sont perdus lors du couplage des deux volants.
L'importance
Comme l'inertie rotationnelle du système a augmenté, la vitesse angulaire a diminué, comme prévu par la loi de conservation du moment cinétique. Dans cet exemple, nous voyons que l'énergie cinétique finale du système a diminué, car de l'énergie est perdue lors de l'accouplement des volants. Comparez cela à l'exemple de la patineuse de Figure\(\PageIndex{1}\) qui travaille pour ramener ses bras vers l'intérieur et y ajouter de l'énergie cinétique de rotation.
Un manège sur une aire de jeux tourne à 4,0 tr/min. Trois enfants sautent à bord et augmentent de 25 % le moment d'inertie du système de rotation du manège et de la rotation pour enfants. Qu'est-ce que le nouveau taux de rotation ?
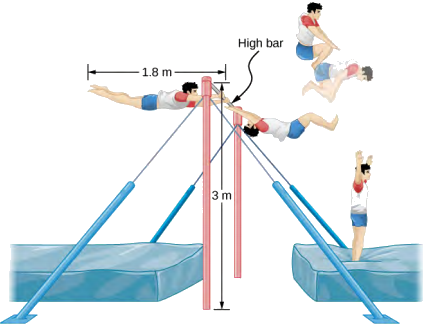
Une gymnaste de 80 kg descend d'une barre haute. Il commence le démontage à pleine extension, puis recule pour effectuer un certain nombre de tours avant d'atterrir. Son moment d'inertie lorsqu'il est complètement déployé peut être estimé comme une tige d'une longueur de 1,8 m et, lorsqu'il est dans la cage, une tige de la moitié de cette longueur. Si sa vitesse de rotation à pleine extension est de 1,0 tr/min et qu'il entre dans le repli alors que son centre de gravité se trouve à 3,0 m de hauteur et se déplace horizontalement vers le sol, combien de tours peut-il exécuter s'il sort du repli à 1,8 m de hauteur ? Voir la figure\(\PageIndex{4}\).
Stratégie
En utilisant la conservation du moment cinétique, nous pouvons déterminer son taux de rotation lorsqu'il est dans le pli. À l'aide des équations de la cinématique, nous pouvons trouver l'intervalle de temps entre une hauteur de 3,0 m et 1,8 m. Comme il se déplace horizontalement par rapport au sol, les équations de chute libre se simplifient. Cela permettra de calculer le nombre de tours pouvant être exécutés. Comme nous utilisons un ratio, nous pouvons conserver les unités en tours par seconde et nous n'avons pas besoin de les convertir en radians/s.
Solution
Le moment d'inertie à pleine extension est\[I_{0} = \frac{1}{12} mL^{2} = \frac{1}{12} (80.0\; kg)(1.8\; m)^{2} = 21.6\; kg\; \cdotp m^{2} \ldotp \nonumber\]
Le moment d'inertie dans le repliement est\[I_{f} = \frac{1}{12} mL_{f}^{2} = \frac{1}{12} (80.0\; kg)(0.9\; m)^{2} = 5.4\; kg\; \cdotp m^{2} \ldotp \nonumber\]
Conservation du moment cinétique :\[I_{f} \omega_{f} = I_{0} \omega_{0} \Rightarrow \omega_{f} = \frac{I_{0} \omega_{0}}{I_{f}} = \frac{(21.6\; kg\; \cdotp m^{2})(1.0\; rev/s)}{5.4\; kg\; \cdotp m^{2}} = 4.0\; rev/s \ldotp \nonumber\]
Intervalle de temps dans le camion :\[t = \sqrt{\frac{2h}{g}} = \sqrt{\frac{2(3.0 - 1.8) m}{9.8\; m/s}} = 0.5\; s \ldotp \nonumber\]
En 0,5 s, il sera capable d'exécuter deux tours à 4,0 tr/min.
L'importance
Notez que le nombre de révolutions qu'il peut effectuer dépend de la durée pendant laquelle il est dans les airs. Dans le problème, il sort de la barre haute horizontalement vers le sol. Il pourrait également sortir en biais par rapport au sol, ce qui lui laisserait plus ou moins de temps dans les airs selon l'angle, positif ou négatif, par rapport au sol. Les gymnastes doivent en tenir compte lorsqu'ils exécutent leurs démontages.
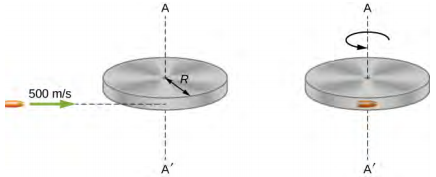
Une balle d'une masse m = 2,0 g se déplace horizontalement à une vitesse de 500,0 m/s. La balle frappe et s'incruste dans le bord d'un disque solide de masse M = 3,2 kg et de rayon R = 0,5 m. Le cylindre est libre de tourner autour de son axe et est initialement au repos (Figure\(\PageIndex{5}\)). Quelle est la vitesse angulaire du disque immédiatement après l'enfoncement de la balle ?
Stratégie
Pour le système de la balle et du cylindre, aucun couple externe n'agit le long de l'axe vertical passant par le centre du disque. Ainsi, le moment cinétique le long de cet axe est conservé. Le moment cinétique initial de la balle est MvR, qui est mesuré autour de l'axe de rotation du disque juste avant la collision. Le moment cinétique initial du cylindre est nul. Ainsi, le moment cinétique net du système est mVr. Le moment cinétique étant conservé, le moment cinétique initial du système est égal au moment cinétique de la balle encastrée dans le disque immédiatement après l'impact.
Solution
Le moment cinétique initial du système est
\[L_{i} = mvR \ldotp \nonumber\]
Le moment d'inertie du système avec la balle encastrée dans le disque est
\[I = mR^{2} + \frac{1}{2} MR^{2} = \left(m + \dfrac{M}{2}\right) R^{2} \ldotp \nonumber\]
Le moment cinétique final du système est
\[L_{f} = I \omega_{f} \ldotp \nonumber\]
Ainsi, par conservation du moment cinétique, L i = L f et
\[mvR = \left(m + \dfrac{M}{2}\right) R^{2} \omega_{f} \ldotp \nonumber\]
Résoudre pour\(\omega_{f}\),
\[\omega_{f} = \frac{mvR}{\left(m + \dfrac{M}{2}\right) R^{2}} = \frac{(2.0 \times 10^{-3}\; kg)(500.0\; m/s)}{(2.0 \times 10^{-3}\; kg + 1.6\; kg)(0.50\; m)} = 1.2\; rad/s \ldotp \nonumber\]
L'importance
Le système est composé à la fois d'une particule ponctuelle et d'un corps rigide. Il faut faire preuve de prudence lors de la formulation du moment cinétique avant et après la collision. Juste avant l'impact, le moment cinétique de la balle est mesuré autour de l'axe de rotation du disque.


