11.3 : Moment cinétique

Last updated
Save as PDF

Page ID: 191270

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objectifs d'apprentissage

Décrire la nature vectorielle du moment cinétique
Détermine le moment cinétique total et le couple autour d'une origine désignée d'un système de particules
Calculez le moment cinétique d'un corps rigide tournant autour d'un axe fixe
Calculez le couple sur un corps rigide tournant autour d'un axe fixe
Utiliser la conservation du moment cinétique dans l'analyse des objets qui modifient leur vitesse de rotation

Pourquoi la Terre continue-t-elle de tourner ? Qu'est-ce qui l'a fait tourner au départ ? Pourquoi l'attraction gravitationnelle de la Terre n'entraîne-t-elle pas l'écrasement de la Lune vers la Terre ? Et comment une patineuse parvient-elle à tourner de plus en plus vite simplement en tirant ses bras vers l'intérieur ? Pourquoi n'a-t-elle pas besoin d'exercer un couple pour tourner plus vite ?

La réponse à ces questions est que, tout comme le mouvement linéaire total (moment) dans l'univers est conservé, le mouvement de rotation total l'est également. Nous appelons le moment cinétique du mouvement de rotation total, la contrepartie rotationnelle du moment linéaire. Dans ce chapitre, nous définissons d'abord puis explorons le moment cinétique à partir de divers points de vue. Cependant, nous étudions d'abord le moment cinétique d'une seule particule. Cela nous permet de développer le moment cinétique d'un système de particules et d'un corps rigide.

Moment cinétique d'une seule particule

La figure$\PageIndex{1}$ montre une particule à une position$\vec{r}$ avec un moment linéaire$\vec{p}$ = m$\vec{v}$ par rapport à l'origine. Même si la particule ne tourne pas autour de son origine, nous pouvons toujours définir un moment cinétique en termes de vecteur de position et de moment linéaire.

Moment cinétique d'une particule

Le moment cinétique$\vec{l}$ d'une particule est défini comme le produit croisé de$\vec{r}$ et$\vec{p}$, et est perpendiculaire au plan contenant$\vec{r}$ et$\vec{p}$ :

\[\vec{l} = \vec{r} \times \vec{p} \ldotp \label{11.5}\]

Un système de coordonnées x y z est affiché dans lequel x pointe hors de la page, y pointe vers la droite et z pointe vers le haut. Le vecteur r pointe de l'origine vers un point du plan x y, dans le premier quadrant. Le vecteur pointe depuis la pointe du vecteur r, selon un angle de thêta dans le sens antihoraire par rapport à la direction du vecteur r, vu de dessus. Les vecteurs r et p se trouvent tous deux dans le plan x y. Le vecteur l pointe vers le haut et est perpendiculaire au plan x y, conformément à la règle de la main droite. Lorsque les doigts de la main droite se recourbent dans le sens inverse des aiguilles d'une montre, vu de dessus, le pouce pointe vers le haut, dans la direction de l. On nous montre également les composantes du vecteur r parallèles et perpendiculaires au vecteur p. Le vecteur r sub-perpendiculaire est la projection du vecteur r perpendiculaire à la direction du vecteur p. — Figure$\PageIndex{1}$ : Dans un espace tridimensionnel, le vecteur de position$\vec{r}$ localise une particule dans le plan xy avec un moment linéaire$\vec{p}$. Le moment cinétique par rapport à l'origine est$\vec{l} = \vec{r} \times \vec{p}$, qui est dans la direction Z. La direction de$\vec{l}$ est donnée par la règle de droite, comme indiqué.

L'objectif de choisir la direction du moment cinétique qui doit être perpendiculaire au plan contenant$\vec{r}$ et$\vec{p}$ est similaire au choix de la direction du couple devant être perpendiculaire au plan de$\vec{r}$ et$\vec{F}$, comme indiqué dans Rotation à axe fixe. L'amplitude du moment cinétique est déterminée à partir de la définition du produit croisé,

\[l = rp \sin \theta,\]

où$\theta$ est l'angle entre$\vec{r}$ et$\vec{p}$. Les unités du moment cinétique sont kg • m ² /s. Comme pour la définition du couple, nous pouvons définir un bras de levier$r_\perp$ qui est la distance perpendiculaire entre le vecteur$\vec{p}$ de moment et l'origine,$r_\perp = r \sin \theta$. Avec cette définition, l'amplitude du moment cinétique devient

\[l = r_{\perp} p = r_{\perp} mv \ldotp\]

Nous voyons que si la direction de$\vec{p}$ est telle qu'elle passe par l'origine, alors$\theta$ = 0, et que le moment cinétique est nul car le bras de levier est nul. À cet égard, l'amplitude du moment cinétique dépend du choix de l'origine. Si nous prenons la dérivée temporelle du moment cinétique, nous arrivons à une expression du couple sur la particule :

\[ \begin{align*} \frac{d \vec{l}}{dt} &= \frac{d \vec{r}}{dt} \times \vec{p} + \vec{r} \times \frac{d \vec{p}}{dt} \\[4pt] &= \vec{v} \times m \vec{v} + \vec{r} \times \frac{d \vec{p}}{dt} \\[4pt] &= \vec{r} \times \frac{d \vec{p}}{dt} \ldotp \end{align*}\]

Nous avons utilisé ici la définition$\vec{p}$ et le fait qu'un vecteur croisé sur lui-même est nul. À partir de la deuxième loi de Newton$\frac{d \vec{p}}{dt} = \sum \vec{F}$, de la force nette agissant sur la particule et de la définition du couple net, nous pouvons écrire

\[\frac{d \vec{l}}{dt} = \sum \vec{\tau} \ldotp \label{11.6}\]

Notez la similitude avec le résultat linéaire de la deuxième loi de Newton,$\frac{d \vec{p}}{dt} = \sum \vec{F}$. La stratégie de résolution de problèmes suivante peut servir de guide pour le calcul du moment cinétique d'une particule.

Stratégie de résolution de problèmes : moment cinétique d'une particule

Choisissez un système de coordonnées autour duquel le moment cinétique doit être calculé.
Écrivez le vecteur de rayon de la particule ponctuelle en notation vectorielle unitaire.
Ecrivez le vecteur de moment linéaire de la particule en notation vectorielle unitaire.
Prenez le produit croisé$\vec{l} = \vec{r} \times \vec{p}$ et utilisez la règle de droite pour déterminer la direction du vecteur de moment cinétique.
Vérifiez s'il existe une dépendance temporelle dans l'expression du vecteur de moment cinétique. Si tel est le cas, il existe un couple autour de l'origine et$\frac{d \vec{l}}{dt} = \sum \vec{\tau}$ utilisez-le pour calculer le couple. S'il n'y a pas de dépendance temporelle dans l'expression du moment cinétique, le couple net est nul.

Exemple$\PageIndex{2}$: Angular Momentum and Torque on a Meteor

Un météore entre dans l'atmosphère de la Terre (Figure$\PageIndex{2}$) et est observé par quelqu'un au sol avant qu'il ne brûle dans l'atmosphère. Le vecteur$\vec{r}$ = 25 km$\hat{i}$ + 25 km$\hat{j}$ donne la position du météore par rapport à l'observateur. Au moment où l'observateur voit le météore, il a un moment linéaire$\vec{p}$ = (15,0 kg) (−2,0 km/s$\hat{j}$) et il accélère à une vitesse constante de 2,0 m/s (²$− \hat{j}$) le long de sa trajectoire, ce qui, pour nos besoins, peut être considéré comme une ligne droite.

Quel est le moment cinétique du météore par rapport à son origine, qui se trouve à l'emplacement de l'observateur ?
Quel est le couple de rotation du météore par rapport à son origine ?

Un système de coordonnées x y est affiché, avec un x positif vers la droite, le long du sol, et un y positif vers le haut. Un observateur est représenté près de l'origine. Un vecteur r est représenté depuis l'origine jusqu'à un météore à certaines grandes coordonnées x positives et positives y. Le vecteur p à l'emplacement du météore pointe vers le bas. — Figure$\PageIndex{2}$ : Un observateur au sol voit un météore$\vec{r}$ en position linéaire$\vec{p}$.

Stratégie

Nous divisons l'accélération en composantes x et y et utilisons les équations cinématiques pour exprimer la vitesse en fonction de l'accélération et du temps. Nous insérons ces expressions dans le moment linéaire, puis nous calculons le moment cinétique à l'aide du produit croisé. Comme les vecteurs de position et de moment se trouvent dans le plan xy, nous nous attendons à ce que le vecteur de moment cinétique se trouve le long de l'axe Z. Pour déterminer le couple, nous prenons la dérivée temporelle du moment cinétique.

Solution

Le météore pénètre dans l'atmosphère terrestre à un angle de 90,0° sous l'horizontale, de sorte que les composantes de l'accélération dans les directions x et y sont

\[a_{x} = 0,\; a_{y} = -2.0\; m/s^{2} \ldotp \nonumber\]

Nous écrivons les vitesses à l'aide des équations cinématiques.

\[v_{x} = 0,\; v_{y} = (-2.0 \times 10^{3}\; m/s) - (2.0\; m/s^{2})t \ldotp \nonumber\]

Le moment cinétique est\[\begin{split} \vec{l} & = \vec{r} \times \vec{p} = (25.0\; km\; \hat{i} + 25.0\; km\; \hat{j}) \times (15.0\; kg)(0 \hat{i} + v_{y} \hat{j}) \\ & = 15.0\; kg [ 25.0\; km (v_{y}) \hat{k}] \\ & = 15.0\; kg \{ (2.50 \times 10^{4}\; m)[(-2.0 \times 10^{3}\; m/s) - (2.0\; m/s^{2})t] \hat{k} \} \ldotp \end{split} \nonumber\] At t = 0, le moment cinétique du météore autour de son origine est\[\vec{l}_{0} = 15.0\; kg [ (2.50 \times 10^{4}\; m)(-2.0 \times 10^{3}\; m/s) \hat{k}] = 7.50 \times 10^{8}\; kg\; \cdotp m^{2}/s (- \hat{k}) \ldotp \nonumber\] C'est l'instant où l'observateur voit le météore.
Pour déterminer le couple, nous prenons la dérivée temporelle du moment cinétique. $\vec{l}$En prenant la dérivée temporelle de en fonction du temps, qui est la deuxième équation immédiatement ci-dessus, nous avons\[\frac{d \vec{l}}{dt} = (-15.0\; kg)(2.50 \times 10^{4}\; m)(2.0\; m/s^{2}) \hat{k} \ldotp \nonumber\] Ensuite, puisque$\frac{d \vec{l}}{dt} = \sum \vec{\tau}$, nous avons\[\sum \vec{\tau} = -7.5 \times 10^{5}\; N\; \cdotp m\; \hat{k} \ldotp \nonumber\] Les unités de couple sont données en newtons-mètres, à ne pas confondre avec les joules. À titre de vérification, nous notons que le bras de levier est la composante X du vecteur$\vec{r}$ de la figure$\PageIndex{2}$ puisqu'il est perpendiculaire à la force agissant sur le météore, qui se trouve le long de sa trajectoire. Selon la deuxième loi de Newton, cette force est $$ \ vec {F} = ma (- \ hat {j}) = (15,0 \ ; kg) (2,0 \ ; m/s^ {2}) (- \ hat {j}) = 30,0 \ ; kg \ ; \ cdotp m/s^ {2} (- \ hat {j}) \ LDotp$Le bras de levier est $$ \ vec {r} _ {\ perp} = 2,5 \ times 10^ {4} \ ; m \ ; \ hat {i} \ LDotp$$Ainsi, le couple est de $$ \ begin {split} \ sum \ vec {\ tau} = \ vec {r} _ {\ perp} \ times \ vec {F } & = (2,5 \ fois 10^ {4} \ ; m \ ; \ hat {i}) \ fois (-30,0 \ ; kg \ ; \ cdotp m/s^ {2} \ ; \ hat {j}), \ \ & = 7,5 \ fois 10^ {5} \ ; N \ ; \ cdotp m (- \ hat {k}) \ ldotp \ end {split} $

L'importance

Comme le météore accélère vers la Terre, son rayon et son vecteur de vitesse changent. Par conséquent$\vec{l} = \vec{r} \times \vec{p}$, depuis, le moment cinétique change en fonction du temps. Le couple exercé sur le météore par rapport à son origine est toutefois constant, car le bras de levier$\vec{r}_{\perp}$ et la force exercée sur le météore sont constants. Cet exemple est important car il montre que le moment cinétique dépend du choix de l'origine à partir de laquelle il est calculé. Les méthodes utilisées dans cet exemple sont également importantes pour développer le moment cinétique d'un système de particules et d'un corps rigide.

Exercice$\PageIndex{1}$

Un proton qui tourne en spirale autour d'un champ magnétique exécute un mouvement circulaire dans le plan du papier, comme indiqué ci-dessous. La trajectoire circulaire a un rayon de 0,4 m et le proton a une vitesse de 4,0 x 10 ⁶ m/s. Quel est le moment cinétique du proton par rapport à son origine ?

Un proton se déplace dans un cercle dans le sens antihoraire. Le cercle a un rayon r. Le proton est représenté lorsqu'il se trouve à droite du centre du cercle, et sa vitesse est v sub-perpendiculaire dans la direction ascendante, positive y.

Moment cinétique d'un système de particules

Le moment cinétique d'un système de particules est important dans de nombreuses disciplines scientifiques, dont l'astronomie. Prenons l'exemple d'une galaxie spirale, d'une île d'étoiles en rotation comme notre propre Voie lactée. Les étoiles individuelles peuvent être traitées comme des particules ponctuelles, chacune ayant son propre moment cinétique. La somme vectorielle des moments angulaires individuels donne le moment cinétique total de la galaxie. Dans cette section, nous développons les outils qui nous permettent de calculer le moment cinétique total d'un système de particules.

Dans la section précédente, nous avons introduit le moment cinétique d'une seule particule autour d'une origine désignée. L'expression de ce moment cinétique est$\vec{l} = \vec{r} \times \vec{p}$, où le vecteur$\vec{r}$ va de l'origine à la particule, et$\vec{p}$ est le moment linéaire de la particule. Si nous avons un système de N particules, chacune ayant un vecteur de position à partir de l'origine donné par$\vec{r}_{i}$ et chacune ayant un moment$\vec{p}_{i}$, alors le moment cinétique total du système de particules autour de l'origine est la somme vectorielle des moments angulaires individuels autour de l'origine. C'est-à-dire

\[\vec{L} = \vec{l}_{1} + \vec{l}_{2} + \cdots + \vec{l}_{N} \ldotp \label{11.7}\]

De même, si la particule i est soumise à un couple net$\vec{\tau_{i}}$ autour de l'origine, alors nous pouvons trouver le couple net autour de l'origine dû au système de particules en différenciant l'équation 11.7 :

\[\frac{d \vec{L}}{dt} = \sum_{i} \frac{d \vec{l}_{i}}{dt} = \sum_{i} \tau_{i} \ldotp\]

La somme des couples individuels produit un couple externe net sur le système, que nous désignons$\sum \vec{\tau}$. Ainsi,

\[\frac{d \vec{L}}{dt} = \sum_{i} \tau_{i} \ldotp \label{11.8}\]

L'équation \ ref {11.8} indique que le taux de variation du moment cinétique total d'un système est égal au couple externe net agissant sur le système lorsque les deux grandeurs sont mesurées par rapport à une origine donnée. L'équation \ ref {11.8} peut être appliquée à tout système ayant un moment cinétique net, y compris les corps rigides, comme indiqué dans la section suivante.

Exemple$\PageIndex{2}$: Angular Momentum of Three Particles

En référence à la figure$\PageIndex{1a}$ :

Déterminez le moment cinétique total dû aux trois particules autour de l'origine.
Quel est le taux de variation du moment cinétique ?

Trois particules dans le plan x y avec des vecteurs de position et de moment différents sont affichées. Les axes x et y indiquent la position en mètres et ont une plage de -4,0 à 4,0 mètres. La particule 1 se trouve à x = -2,0 mètres et y = 1,0 mètre, m sub 1 est égal à 2,0 kilogrammes, v sub 1 est à 4,0 j à 9 mètres par seconde, vers le haut, et F sub 1 est à -6,0 i hat Newtons vers la gauche. La particule 2 se trouve à x = 4,0 mètres et y = 1,0 mètre, m sub 2 est égal à 4,0 kilogrammes, v sub 2 est à 5,0 i hat mètres par seconde, vers la droite, et F sub 2 est à 10,0 j à Newtons plus haut. La particule 3 se trouve à x = 2,0 mètres et y = -2,0 mètres, m sub 3 est égal à 1,0 kilogramme, v sub 3 est à 3,0 i hat mètres par seconde, vers la droite, et F sub 3 est à -8,0 j à Newtons plus bas. — Figure$\PageIndex{3}$ : Trois particules dans le plan xy avec des vecteurs de position et de moment différents.

Stratégie

Notez les vecteurs de position et de moment pour les trois particules. Calculez les moments angulaires individuels et ajoutez-les sous forme de vecteurs pour trouver le moment cinétique total. Ensuite, faites de même pour les couples.

Solution

Particule 1 : $$ \ vec {r} _ {1} = -2,0 \ ; m \ ; \ hat {i} + 1,0 \ ; m \ ; \ hat {j}, \ ; \ vec {p} _ {1} = (2,0 \ ; kg) (4,0 \ ; m/s \ ; \ hat {j}) = 8,0 \ ; kg \ ; \ cdotp m/s \ ; \ chapeau {j} $ $$ \ vec {l} _ {1} = \ vec {r} _ {1} \ times \ vec {p} _ {1} = -16,0 \ ; kg \ ; \ cdotp m^ {2} /s \ ; \ hat {k} \ ldotp$$ Particule 2 : $$ \ vec {r} _ {2} = 4,0 \ ; m \ ; \ hat {i} 1,0 \ ; m \ ; \ chapeau {j}, \ ; \ vec {p} _ {2} = (4,0 \ ; kg) (5,0 \ ; m/s \ ; \ hat {i}) = 20,0 \ ; kg \ ; \ cdotp m/s \ ; \ hat {i}, $ $ \ vec {l} _ {2} = \ vec {r} _ {2} \ times \ vec {p} _ {2} = -20,0 \ ; kg \ ; \ cdotp m^ {2} /s \ ; \ hat {k} \ LDotp$$Particule 3 : $ \ vec {r} _ {3} = 2,0 \ ; m \ ; \ hat {i} - 2,0 \ ; m \ ; \ hat {j}, \ ; \ vec {p} _ {3} = (1,0 \ ; kg) (3,0 \ ; m/s \ ; \ hat {i}) = 3,0 \ ; kg \ ; \ cdotp m/s \ ; \ hat {j}, $$ $$ \ vec {l} _ {3} = \ vec {r} _ {3} \ times \ vec {p} _ {3} = 6,0 \ ; kg \ ; \ cdotp m^ {2} /s \ ; \ hat {k} \ LDotp$$Nous ajoutons les moments angulaires individuels pour trouver le total concernant l'origine : $$ \ vec {l} _ {T} = \ vec {l} _ {1} + \ vec {l} _ {2} + \ vec {l} _ {3} = -30 \ ; kg \ ; \ cdotp m^ {2} /s \ ; \ chapeau {k} \ ldotp$$
Les forces individuelles et les bras de levier sont $$ \ begin {split} \ vec {r} _ {1 \ perp} & = 1,0 \ ; m \ ; \ hat {j}, \ ; \ vec {F} _ {1} = -6,0 \ ; N \ ; \ hat {i}, \ ; \ vec {\ tau} _ {1} = 6,0 \ ; N \ ; \ cdotp m \ ; hat {k} \ \ \ vec {r} _ {2 \ perp} & = 4,0 \ ; m \ ; \ hat {i}, \ ; \ vec {F} _ {2} = 10,0 \ ; N \ ; \ hat {i}, \ ; \ vec {\ tau} _ {2} = 40,0 \ ; N \ ; \ cdotp m \ ; \ hat {k} \ \ \ vec {r} _ {3 \ perp} & = 2,0 \ ; m \ ; \ hat {j}, \ ; \ vec {F} _ {3} = -8,0 \ ; N \ ; \ hat {j}, \ ; \ vec {\ tau} _ {3} = -16,0 \ ; N \ ; \ cdotp m \ ; \ chapeau {k} \ ldotp \ end {split} $$Donc : $$ \ sum_ {i} \ vec {\ tau} _ {i} = \ vec {\ tau} _ {1} + \ vec {\ tau} _ {2} + \ vec {\ tau} _ {3} = 30 \ ; N \ ; \ cdotp m \ ; \ hat {k} \ ldotp$$

L'importance

Cet exemple illustre le principe de superposition du moment cinétique et du couple d'un système de particules. Lors de l'évaluation$\vec{r}_{i}$ des vecteurs de rayon des particules pour calculer les moments angulaires, et des bras de levier,$\vec{r}_{i \perp}$ pour calculer les couples, il faut faire attention, car il s'agit de quantités complètement différentes.

Moment cinétique d'un corps rigide

Nous avons étudié le moment cinétique d'une seule particule, que nous avons généralisé à un système de particules. Nous pouvons maintenant utiliser les principes abordés dans la section précédente pour développer le concept du moment cinétique d'un corps rigide. Les objets célestes tels que les planètes ont un moment cinétique dû à leur rotation et à leur orbite autour des étoiles. En ingénierie, tout ce qui tourne autour d'un axe est soumis à un moment cinétique, comme les volants, les hélices et les pièces rotatives des moteurs. La connaissance des moments angulaires de ces objets est cruciale pour la conception du système dans lequel ils font partie.

Pour développer le moment cinétique d'un corps rigide, nous modélisons un corps rigide comme étant composé de petits segments de masse,$\Delta$ m _i. Dans la figure$\PageIndex{4}$, un corps rigide est contraint de tourner autour de l'axe Z avec une vitesse angulaire$\omega$. Tous les segments de masse qui constituent le corps rigide subissent un mouvement circulaire autour de l'axe Z avec la même vitesse angulaire. La partie (a) de la figure montre le segment de masse$\Delta$ m _i avec le vecteur$\vec{r}_{i}$ de position depuis l'origine et le rayon R _i jusqu'à l'axe Z. L'amplitude de sa vitesse tangentielle est v _i = R _i$\omega$. Comme les vecteurs A$\vec{v}_{i}$ et$\vec{r}_{i}$ sont perpendiculaires l'un à l'autre, l'amplitude du moment cinétique de ce segment de masse est

\[l_{i} = r_{i} (\Delta mv_{i}) \sin 90^{o} \ldotp\]

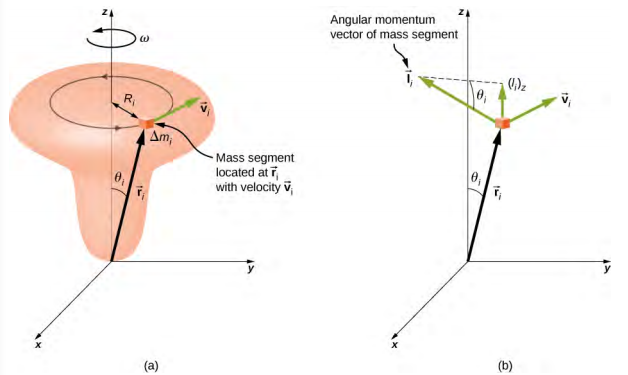
La figure a montre un objet en forme de poignée de porte et un système de coordonnées x y z. L'objet est disposé verticalement et centré sur l'axe z, avec le bouton large en haut. L'objet tourne autour de l'axe z, dans le sens antihoraire vu de dessus, avec une vitesse angulaire oméga. Une petite partie de l'objet est mise en évidence. Ce segment de masse, étiqueté Delta m sub i, est situé au niveau du vecteur r sub i, se déplace avec le vecteur de vitesse v sub i et trace un cercle dans le sens antihoraire de rayon R sub i. Le vecteur r sub i s'étend de l'origine au segment de masse et fait un angle de theta sub i avec l'axe z. Le vecteur v sub i est tangent au cercle tracé par le segment de masse. La figure b montre le système de coordonnées x y et le segment de masse. Les vecteurs r sub i et v sub i sont à nouveau représentés, de même que l'angle theta sub i entre le vecteur r sub i et l'axe z. Le vecteur de moment cinétique du segment de masse, vecteur l sub i, est également indiqué. Le vecteur l sub i est perpendiculaire à la fois à r et à v, comme indiqué par la règle de droite, et possède une composante z vers le haut, indiquée sur le diagramme et étiquetée l sub i z. Le côté restant du triangle droit dont l'hypoténuse est l sub i et le côté vertical est l sub i z est représenté par une ligne pointillée. L'angle adjacent à ce côté, et opposé au côté vertical l sub i z, est thêta sub i. — Figure$\PageIndex{4}$ : (a) Un corps rigide est contraint de tourner autour de l'axe Z. Le corps rigide est symétrique par rapport à l'axe Z. Un segment de masse$\Delta$ m _i est situé à la position$\vec{r}_{i}$ qui forme un angle$\theta_{i}$ par rapport à l'axe Z. Le mouvement circulaire d'un segment de masse infinitésimal est illustré. (b)$\vec{l}_{i}$ est le moment cinétique du segment de masse et possède une composante le long de l'axe _{z ($\vec{l}_{i}$) z.}

En utilisant la règle de la main droite, le vecteur du moment cinétique pointe dans la direction indiquée sur la figure$\PageIndex{4b}$. La somme des moments angulaires de tous les segments de masse contient des composantes situées à la fois le long et perpendiculairement à l'axe de rotation. Chaque segment de masse possède une composante perpendiculaire du moment cinétique qui sera annulée par la composante perpendiculaire d'un segment de masse identique sur le côté opposé du corps rigide. Ainsi, la composante située le long de l'axe de rotation est la seule qui donne une valeur non nulle lorsqu'elle est additionnée sur tous les segments de masse. À partir de la partie (b), la composante du$\vec{l}_{i}$ long de l'axe de rotation est

\[\begin{split} (l_{i})_{z} & = l_{i} \sin \theta_{i} = (r_{i} \Delta m_{i} v_{i}) \sin \theta_{i}, \\ & = (r_{i} \sin \theta_{i})(\Delta m_{i} v_{i}) = R_{i} \Delta m_{i} v_{i} \ldotp \end{split}\]

Le moment cinétique net du corps rigide le long de l'axe de rotation est

\[L = \sum_{i} (\vec{l}_{i})_{z} = \sum_{i} R_{i} \Delta m_{i} v_{i} = \sum_{i} R_{i} \Delta m_{i} (R_{i} \omega) = \omega \sum_{i} \Delta m_{i} (R_{i})^{2} \ldotp\]

La sommation$\sum_{i} \Delta$ (R _i) ² est simplement le moment d'inertie I du corps rigide autour de l'axe de rotation. Pour un arceau mince tournant autour d'un axe perpendiculaire au plan de l'arceau, tous les R _i sont égaux à R, de sorte que la somme se réduit à R ²$\sum_{i} \Delta$ m _i = mR ², qui est le moment d'inertie pour un arceau mince illustré à la Figure 10.20. Ainsi, l'amplitude du moment cinétique le long de l'axe de rotation d'un corps rigide tournant avec une vitesse angulaire$\omega$ autour de l'axe est

\[L = I \omega \ldotp \label{11.9}\]

Cette équation est analogue à l'amplitude du moment linéaire p = mv. La direction du vecteur de moment cinétique est dirigée le long de l'axe de rotation donné par la règle de droite.

Exemple$\PageIndex{3}$: Angular Momentum of a Robot Arm

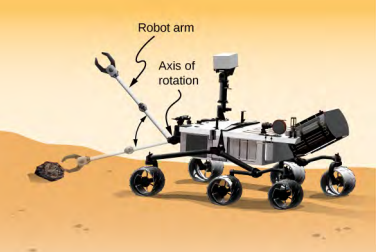
Un bras de robot sur un rover martien tel que Curiosity, illustré sur la$\PageIndex{5}$ figure, mesure 1 m de long et possède une pince à son extrémité libre pour ramasser les roches. La masse du bras est de 2,0 kg et celle de la pince est de 1,0 kg (Figure$\PageIndex{5}$). Le bras et la pince du robot passent du repos à$\omega$ = 0,1$\pi$ rad/s en 0,1 s. Il pivote vers le bas et ramasse une roche martienne d'une masse de 1,5 kg. L'axe de rotation est le point où le bras du robot se connecte au rover.

Quel est le moment cinétique du bras du robot lui-même par rapport à l'axe de rotation après 0,1 s lorsque le bras a cessé d'accélérer ?
Quel est le moment cinétique du bras du robot lorsqu'il a la roche martienne dans sa pince et qu'il tourne vers le haut ?
Lorsque le bras n'a pas de pierre dans la pince, quel est le couple autour du point où le bras se connecte au rover lorsqu'il accélère entre l'arrêt et sa vitesse angulaire finale ?

Une illustration du rover martien. Un bras muni d'une griffe à son extrémité part d'une extrémité du rover et peut pivoter de haut en bas pour ramasser une pierre. L'axe de rotation est le point où le bras du robot se connecte au rover. — Figure$\PageIndex{5}$ : Un bras de robot monté sur un rover martien bascule vers le bas et ramasse une roche martienne. (crédit : modification des travaux par la NASA/JPL-Caltech)

Stratégie

Nous utilisons l'équation \ ref {11.9} pour déterminer le moment cinétique dans les différentes configurations. Lorsque le bras tourne vers le bas, la règle de droite donne le vecteur de moment cinétique dirigé hors de la page, que nous appellerons la direction z positive. Lorsque le bras tourne vers le haut, la règle de droite indique la direction du vecteur de moment cinétique dans la page ou dans la direction znégative. Le moment d'inertie est la somme des moments d'inertie individuels. Le bras peut être approché à l'aide d'une tige solide, et la pince et la roche martienne peuvent être approximées sous forme de masses ponctuelles situées à une distance de 1 m de l'origine. Pour la partie (c), nous utilisons la deuxième loi du mouvement de Newton pour la rotation afin de déterminer le couple sur le bras du robot.

Solution

En notant les différents moments d'inertie, nous avons

Bras de robot :\[I_{R} = \frac{1}{3} m_{R} r^{2} = \frac{1}{3} (2.00\; kg)(1.00\; m)^{2} = \frac{2}{3}\; kg\; \cdotp m^{2} \ldotp\]
Pinces :\[I_{F} = m_{F} r^{2} = (1.0\; kg)(1.0\; m)^{2} = 1.0\; kg\; \cdotp m^{2} \ldotp\]
Roche martienne :\[I_{MR} = m_{MR} r^{2} = (1.5\; kg)(1.0\; m)^{2} = 1.5\; kg\; \cdotp m^{2} \ldotp\]

Par conséquent, sans la roche martienne, le moment total d'inertie est

\[I_{Total} = I_{R} + I_{F} = 1.67\; kg\; \cdotp m^{2}\]

et l'amplitude du moment cinétique est

\[L = I \omega = (1.67\; kg\; \cdotp m^{2})(0.1 \pi\; rad/s) = 0.17 \pi\; kg\; \cdotp m^{2}/s \ldotp\]

Le vecteur de moment cinétique est dirigé hors de la page dans la$\hat{k}$ direction dans laquelle le bras du robot tourne dans le sens antihoraire.

Nous devons inclure la roche martienne dans le calcul du moment d'inertie, donc nous l'avons fait\[I_{Total} = I_{R} + I_{F} + I_{MR} = 3.17\; kg\; \cdotp m^{2}\] et\[L = I \omega = (3.17\; kg\; \cdotp m^{2})(0.1 \pi\; rad/s) = 0.32 \pi\; kg\; \cdotp m^{2}/s \ldotp\] maintenant le vecteur du moment cinétique est dirigé dans la page dans la$− \hat{k}$ direction, selon la règle de la main droite, puisque le bras du robot tourne maintenant dans le sens des aiguilles d'une montre.
Nous trouvons le couple lorsque le bras ne possède pas de roche en prenant la dérivée du moment cinétique à l'aide de l'équation \ ref {11.8}$\frac{d \vec{L}}{dt} = \sum \vec{\tau}$. Mais puisque L = I$\omega$, et sachant que la direction des vecteurs de moment cinétique et de couple se situe le long de l'axe de rotation, nous pouvons supprimer la notation vectorielle et déterminer\[\frac{dL}{dt} = \frac{d (I \omega)}{dt} = I \frac{d \omega}{dt} = I \alpha = \sum \tau,\] quelle est la deuxième loi de Newton pour la rotation. Depuis$\alpha = \frac{0.1 \pi\; rad/s}{0.1\; s} = \pi\; rad/s^{2}$, on peut calculer le couple net :\[\sum \tau = I \alpha = (1.67\; kg\; \cdotp m^{2})(\pi\; rad/s^{2}) = 1.67 \pi\; N\; \cdotp m \ldotp\]

L'importance

Le moment cinétique dans (a) est inférieur à celui de (b) du fait que le moment d'inertie dans (b) est supérieur à (a), alors que la vitesse angulaire est la même.

Exercice$\PageIndex{3}$

Lequel a le plus grand moment cinétique : une sphère solide de masse m tournant à une fréquence angulaire constante$\omega_{0}$ autour de l'axe z, ou un cylindre plein de même masse et de même vitesse de rotation autour de l'axe z ?

Simulation

Visitez la simulation interactive du moment cinétique de l'Université du Colorado pour en savoir plus sur le moment cinétique.

Moment cinétique d'une particule

Stratégie de résolution de problèmes : moment cinétique d'une particule

Exemple\(\PageIndex{2}\): Angular Momentum and Torque on a Meteor

Solution

Exercice\(\PageIndex{1}\)

Exemple\(\PageIndex{2}\): Angular Momentum of Three Particles

Solution

Exemple\(\PageIndex{3}\): Angular Momentum of a Robot Arm

Solution

Exercice\(\PageIndex{3}\)

Simulation