Skip to main content
Global

11.2 : Rolling Motion

  1. Last updated
  2. Save as PDF
  • Page ID
    191262

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objectifs d'apprentissage
    • Décrire la physique du mouvement de roulement sans glissement
    • Expliquer comment les variables linéaires sont liées aux variables angulaires dans le cas d'un mouvement de roulement sans glissement
    • Trouvez les accélérations linéaires et angulaires en mouvement de roulement avec et sans glissement
    • Calculez la force de friction statique associée au mouvement de roulement sans glissement
    • Utilisez les économies d'énergie pour analyser le mouvement de roulement

    Le mouvement de roulement est cette combinaison courante de mouvement de rotation et de translation que nous voyons partout, tous les jours. Réfléchissez aux différentes situations où des roues se déplacent sur une voiture le long d'une autoroute, des roues d'un avion atterrissant sur une piste ou des roues d'un explorateur robotique sur une autre planète. La compréhension des forces et des couples impliqués dans le mouvement de roulement est un facteur crucial dans de nombreux types de situations.

    Pour analyser le mouvement de roulement dans ce chapitre, reportez-vous à la Figure 10.5.4 de Rotation à axe fixe pour déterminer les moments d'inertie de certains objets géométriques courants. Vous pouvez également le trouver utile dans d'autres calculs impliquant une rotation.

    Mouvement de roulement sans glisser

    Depuis l'invention de la roue, les gens observent le mouvement de roulement sans glisser. Par exemple, nous pouvons examiner l'interaction entre les pneus d'une voiture et la surface de la route. Si le conducteur appuie sur l'accélérateur jusqu'au sol, de telle sorte que les pneus patinent sans que la voiture avance, il doit y avoir une friction cinétique entre les roues et la surface de la route. Si le conducteur appuie lentement sur l'accélérateur, ce qui fait avancer la voiture, les pneus roulent sans glisser. La plupart des gens s'étonnent qu'en fait, le bas de la roue soit au repos par rapport au sol, ce qui indique qu'il doit y avoir une friction statique entre les pneus et la surface de la route. Dans la figure\(\PageIndex{1}\), le vélo est en mouvement et le cycliste reste debout. Les pneus entrent en contact avec la surface de la route et, même s'ils roulent, leur partie inférieure se déforme légèrement, ne glisse pas et reste au repos par rapport à la surface de la route pendant une durée mesurable. Pour ce faire, il doit y avoir une friction statique entre le pneu et la surface de la route.

    La figure a est une photographie d'une personne faisant du vélo. La caméra a suivi le vélo, de sorte que l'image du vélo et du cycliste est nette, l'arrière-plan est flou à cause du mouvement du vélo. La figure b est une photographie d'une roue de vélo roulant sur le sol, l'appareil photo étant immobile par rapport au sol. La roue et les rayons sont flous en haut mais clairs en bas.
    Figure\(\PageIndex{1}\) : (a) Le vélo avance et ses pneus ne glissent pas. Le bas du pneu légèrement déformé reste au repos par rapport à la surface de la route pendant une durée mesurable. (b) Cette image montre que le haut d'une roue roulante semble flou à cause de son mouvement, mais que le bas de la roue est instantanément au repos. (crédit a : modification d'une œuvre par Nelson Lourenço ; crédit b : modification d'une œuvre par Colin Rose)

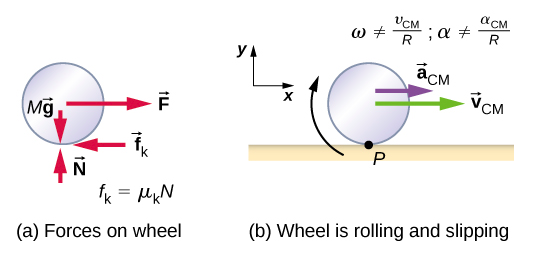
    Pour analyser le roulage sans glissement, nous dérivons d'abord les variables linéaires de vitesse et d'accélération du centre de masse de la roue en termes de variables angulaires qui décrivent le mouvement de la roue. La situation est illustrée dans la figure\(\PageIndex{2}\).

    La figure a montre le schéma du corps libre d'une roue, y compris l'endroit où les forces agissent. Quatre forces sont représentées : M g est une force dirigée vers le bas qui agit sur le centre de la roue. N est une force ascendante agissant sur le bas de la roue. F est une force dirigée vers la droite, agissant sur le centre de la roue, et f sub s est une force dirigée vers la gauche agissant sur le bas de la roue. La force f sub s est inférieure ou égale à mu sub s fois N. La figure b est une illustration d'une roue roulant sans glisser sur une surface horizontale. Le point P est le point de contact entre le bas de la roue et la surface. La roue a une rotation dans le sens des aiguilles d'une montre, une accélération vers la droite d'un sous-C M et une vitesse vers la droite de v sub V M. Les relations omega est égal à v sub C M sur R et alpha est égal à un sub C M sur R sont données. Un système de coordonnées avec un x positif vers la droite et un y vers le haut est affiché. La figure c montre la roue au centre du châssis. Le point P a un vecteur de vitesse dans la direction négative par rapport au centre de masse de la roue. Ce vecteur est indiqué sur le diagramme et étiqueté comme moins R oméga i. Il est tangent à la roue en bas et pointe vers la gauche. Des vecteurs supplémentaires situés à différents endroits sur la jante de la roue sont représentés, tous tangents à la roue et orientés dans le sens des aiguilles d'une montre.
    Figure\(\PageIndex{2}\) : (a) Une roue est tirée sur une surface horizontale par une force\(\vec{F}\). La force de friction statique\(\vec{f}_{s}\),\(|\vec{f}_{s}|\) ≤\(\mu_{s}\) N, est suffisamment grande pour l'empêcher de glisser. (b) Les vecteurs de vitesse linéaire et d'accélération du centre de masse et les expressions pertinentes pour\(\omega\) et\(\alpha\). Le point P est au repos par rapport à la surface. (c) Par rapport au cadre du centre de masse (CM), le point P a une vitesse linéaire −R\(\omega \hat{i}\).

    Sur la Figure\(\PageIndex{2}\) (a), nous voyons les vecteurs de force impliqués dans la prévention du patinage de la roue. Dans (b), le point P qui touche la surface est au repos par rapport à la surface. Par rapport au centre de masse, le point P a une vitesse −R\(\omega \hat{i}\), où R est le rayon de la roue et\(\omega\) la vitesse angulaire de la roue autour de son axe. Comme la roue roule, la vitesse de P par rapport à la surface est sa vitesse par rapport au centre de masse augmentée de la vitesse du centre de masse par rapport à la surface :

    \[\vec{v}_{P} = -R \omega \hat{i} + v_{CM} \hat{i} \ldotp\]

    Puisque la vitesse de P par rapport à la surface est nulle, v P = 0, cela signifie que

    \[v_{CM} = R \omega \ldotp \label{11.1}\]

    Ainsi, la vitesse du centre de gravité de la roue est son rayon multiplié par la vitesse angulaire autour de son axe. Nous montrons la correspondance entre la variable linéaire sur le côté gauche de l'équation et la variable angulaire sur le côté droit de l'équation. Ceci est fait ci-dessous pour l'accélération linéaire.

    Si nous différencions l'équation \ ref {11.1} sur le côté gauche de l'équation, nous obtenons une expression pour l'accélération linéaire du centre de masse. Sur le côté droit de l'équation, R est une constante et depuis\(\alpha = \frac{d \omega}{dt}\), nous avons

    \[a_{CM} = R \alpha \ldotp \label{11.2}\]

    De plus, nous pouvons trouver la distance parcourue par la roue en termes de variables angulaires en nous référant à la Figure\(\PageIndex{3}\). Lorsque la roue roule d'un point A à un point B, sa surface extérieure correspond exactement au sol selon la distance parcourue, qui est d CM.

    Nous voyons sur la figure\(\PageIndex{3}\) que la longueur de la surface extérieure qui correspond au sol est la longueur de l'arc\(\theta\) R. En assimilant les deux distances, nous obtenons

    \[d_{CM} = R \theta \ldotp \label{11.3}\]

    Une roue, de rayon R, roulant sur une surface horizontale et se déplaçant vers la droite en v sub C M est tracée dans deux positions. Dans la première position, le point A de la roue se trouve en bas, en contact avec la surface, et le point B est en haut. La longueur de l'arc de A à B le long de la jante de la roue est surlignée et étiquetée comme étant R thêta. Dans la seconde position, le point B de la roue se trouve en bas, en contact avec la surface, et le point A est en haut. La distance horizontale entre le point de contact de la roue avec la surface dans les deux positions illustrées est d sub C M. La longueur de l'arc A B se trouve maintenant de l'autre côté de la roue.
    Figure\(\PageIndex{3}\) : Lorsque la roue roule sur la surface, la longueur d'arc R\(\theta\) de A à B correspond à la surface, correspondant à la distance d CM parcourue par le centre de gravité.
    Exemple\(\PageIndex{1}\): Rolling Down an Inclined Plane

    Un cylindre plein roule le long d'un plan incliné sans glisser, en partant du repos. Il a une masse m et un rayon r. (a) Quelle est son accélération ? b) À quelles conditions le coefficient de frottement statique doit-il\(\mu_{S}\) satisfaire pour que le cylindre ne glisse pas ?

    Stratégie

    Dessinez une esquisse et un diagramme à corps libre, puis choisissez un système de coordonnées. Nous plaçons x dans la direction du bas du plan et y vers le haut perpendiculairement au plan. Identifiez les forces impliquées. Il s'agit de la force normale, de la force de gravité et de la force due au frottement. Écrivez les lois de Newton dans les directions x et y, et la loi de Newton pour la rotation, puis résolvez l'accélération et la force dues à la friction.

    Solution
    1. Le schéma du corps libre et le croquis sont illustrés sur la figure\(\PageIndex{4}\), y compris la force normale, les composantes du poids et la force de friction statique. Il y a à peine assez de friction pour que le cylindre continue de rouler sans glisser. Comme il n'y a pas de glissement, l'amplitude de la force de frottement est inférieure ou égale à\(\mu_{S}\) N. En écrivant les lois de Newton dans les directions x et y, nous avons

    \[\sum F_{x} = ma_{x};\; \sum F_{y} = ma_{y} \ldotp\]

    Schéma d'un cylindre roulant sans glisser sur un plan incliné et schéma du corps libre du cylindre. Sur la gauche se trouve une illustration du plan incliné, qui forme un angle thêta avec l'horizontale. Le cylindre est montré comme étant au repos en haut, puis se déplaçant le long de la pente lorsqu'il est plus bas. Sur la droite se trouve un schéma corporel gratuit. Le système de coordonnées x y est incliné de telle sorte que la direction x positive soit parallèle au plan incliné et pointe vers son bas, et que la direction y positive soit orientée vers l'extérieur, perpendiculaire au plan. Quatre forces sont présentées. N j hat agit au centre du cylindre et pointe dans la direction positive y. m g sine thêta i hat agit au centre du cylindre et pointe dans la direction positive x. Moins m g cosinus thêta j qui agit au centre du cylindre et pointe dans la direction négative y. Moins f sub s est ce qui agit au point de contact et pointe dans la direction x négative.
    Figure\(\PageIndex{4}\) : Un cylindre plein roule sur un plan incliné sans glisser. Le système de coordonnées a x dans la direction descendante du plan incliné et y est perpendiculaire au plan. Le diagramme du corps libre est représenté avec la force normale, la force de friction statique et les composantes du poids\(\vec{g}\) m. La friction fait rouler le cylindre dans l'avion plutôt que de glisser.

    Substituer à partir du diagramme du corps libre

    \[\begin{split} mg \sin \theta - f_{s} & = m(a_{CM}) x, \\ N - mg \cos \theta & = 0 \end{split}\]

    nous pouvons ensuite résoudre l'accélération linéaire du centre de masse à partir de ces équations :

    \[a_{CM} = g\sin \theta - \frac{f_s}{m} \ldotp\]

    Cependant, il est utile d'exprimer l'accélération linéaire en termes de moment d'inertie. Pour cela, nous écrivons la deuxième loi de Newton pour la rotation,

    \[\sum \tau_{CM} = I_{CM} \alpha \ldotp\]

    Les couples sont calculés autour de l'axe passant par le centre de masse du cylindre. Le seul couple non nul est fourni par la force de friction. Nous avons

    \[f_{s} r = I_{CM} \alpha \ldotp\]

    Enfin, l'accélération linéaire est liée à l'accélération angulaire par

    \[(a_{CM})_{x} = r \alpha \ldotp\]

    Ces équations peuvent être utilisées pour résoudre un CM\(\alpha\),, et f S en termes de moment d'inertie, lorsque nous avons abandonné l'indice X. Nous écrivons un CM en termes de composante verticale de la gravité et de la force de friction, et effectuons les substitutions suivantes.

    \[f_{S} = \frac{I_{CM} \alpha}{r} = \frac{I_{CM} a_{CM}}{r^{2}}\]

    De là, nous obtenons

    \[\begin{split} a_{CM} & = g \sin \theta - \frac{I_{CM} a_{CM}}{mr^{2}}, \\ & = \frac{mg \sin \theta}{m + \left(\dfrac{I_{CM}}{r^{2}}\right)} \ldotp \end{split}\]

    Notez que ce résultat est indépendant du coefficient de frottement statique,\(\mu_{s}\).

    Comme nous avons un cylindre plein, d'après la Figure 10.5.4, nous avons I CM =\(\frac{mr^{2}}{2}\) et

    \[a_{CM} = \frac{mg \sin \theta}{m + \left(\dfrac{mr^{2}}{2r^{2}}\right)} = \frac{2}{3} g \sin \theta \ldotp\]

    Par conséquent, nous avons

    \[\alpha = \frac{a_{CM}}{r} = \frac{2}{3r} g \sin \theta \ldotp\]

    1. Comme il ne se produit pas de glissement, f S ≤\(\mu_{s}\) N. En résolvant la force de friction, $$f_ {s} = I_ {CM} \ frac {\ alpha} {r} = I_ {CM} \ frac {(a_ {CM})} {r^ {2}} = \ left (\ dfrac {I_ {CM}} {r^ {2}} \ right) \ left (\ dfrac {I_ {CM}} {r^ {2}} \ right) \ left (\ dfrac {I_ {CM}} frac {mg \ sin \ thêta} {m + \ left (\ dfrac {I_ {CM}} {r^ {2}} \ right)} \ right) = \ frac {mg I_ {CM} \ sin \ thêta} {mr^ {2} + I_ {CM}} \ LDotp$$En substituant cette expression à la condition d'absence de glissement, et en notant que N = mg cos\(\theta\), nous avons $$ \ frac {mg I_ {CM} \ sin \ theta} {mr^ {2} + I_ {CM}} \ leq \ mu_ {s} mg \ cos \ theta$$or $$ \ mu_ {s} \ geq \ frac {\ tan \ theta} {1 + \ left (\ dfrac {mr^ {2}} {I_ {CM}} \ right)} \ lDotp$$Pour le solide cylindre, cela devient $$ \ mu_ {s} \ geq \ frac {\ tan \ theta} {1 + \ left (\ dfrac {2mr^ {2}}} {mr^ {2}} \ right)} = \ frac {1} {3} \ tan \ theta \ ldotp$$

    L'importance

    1. L'accélération linéaire est linéairement proportionnelle au péché\(\theta\). Ainsi, plus l'angle de l'inclinaison est grand, plus l'accélération linéaire est importante, comme on pouvait s'y attendre. L'accélération angulaire est cependant linéairement proportionnelle au sin\(\theta\) et inversement proportionnelle au rayon du cylindre. Ainsi, plus le rayon est grand, plus l'accélération angulaire est faible.
    2. Pour qu'aucun glissement ne se produise, le coefficient de frottement statique doit être supérieur ou égal à\(\frac{1}{3}\) tan\(\theta\). Ainsi, plus l'angle d'inclinaison est grand, plus le coefficient de frottement statique doit être élevé pour empêcher le cylindre de glisser.
    Exercice\(\PageIndex{2}\)

    Un cylindre creux est incliné à un angle de 60°. Le coefficient de frottement statique sur la surface est\(\mu_{s}\) = 0,6. a) Le cylindre roule-t-il sans glisser ? (b) Un cylindre plein roulera-t-il sans glisser ?

    Il est intéressant de répéter l'équation dérivée dans cet exemple pour l'accélération d'un objet qui roule sans glisser :

    \[a_{CM} = \frac{mg \sin \theta}{m + \left(\dfrac{I_{CM}}{r^{2}}\right)} \ldotp \label{11.4}\]

    Il s'agit d'une équation très utile pour résoudre les problèmes liés au roulage sans glissement. Notez que l'accélération est inférieure à celle d'un objet glissant sur un plan sans friction sans rotation. L'accélération sera également différente pour deux cylindres rotatifs ayant des inerties de rotation différentes.

    Mouvement de roulement avec glissement

    Dans le cas d'un mouvement de roulement avec glissement, il faut utiliser le coefficient de frottement cinétique, qui donne naissance à la force de frottement cinétique car aucun frottement statique n'est présent. La situation est illustrée dans la figure\(\PageIndex{5}\). En cas de glissement, v CM − R ↓ 0\(\omega\), car le point P de la roue n'est pas au repos sur la surface, et v P ↓ 0. Ainsi,\(\omega\) σ\(\frac{v_{CM}}{R}\),\(\alpha \neq \frac{a_{CM}}{R}\).

    La figure a montre le schéma du corps libre d'une roue, y compris l'endroit où les forces agissent. Quatre forces sont représentées : M g est une force dirigée vers le bas qui agit sur le centre de la roue. N est une force ascendante agissant sur le bas de la roue. F est une force dirigée vers la droite, agissant sur le centre de la roue, et f sub k est une force dirigée vers la gauche agissant sur le bas de la roue. La force f sub k est égale à mu sub k fois N. La figure b est une illustration du roulement et du glissement de la roue sur une surface horizontale. La roue a une rotation dans le sens des aiguilles d'une montre, une accélération vers la droite d'un sous-C M et une vitesse vers la droite de v sub V M. omega n'est pas égal à v sub C M sur R et alpha n'est pas égal à un sub C M sur R. Un système de coordonnées avec un x positif à droite et un y up positif est affiché.
    Figure\(\PageIndex{5}\) : (a) Un frottement cinétique se produit entre la roue et la surface lorsque la roue glisse. (b) Les relations simples entre les variables linéaires et angulaires ne sont plus valides.
    Exemple\(\PageIndex{2}\): Rolling Down an Inclined Plane with Slipping

    Un cylindre plein roule le long d'un plan incliné à partir du repos et glisse (Figure\(\PageIndex{6}\)). Il a une masse m et un rayon r. (a) Quelle est son accélération linéaire ? (b) Quelle est son accélération angulaire autour d'un axe passant par le centre de gravité ?

    Stratégie

    Dessinez un croquis et un diagramme du corps libre montrant les forces impliquées. Le schéma du corps libre est similaire à celui du boîtier antidérapant, à l'exception de la force de friction, qui est cinétique et non statique. Utilisez la deuxième loi de Newton pour résoudre l'accélération dans la direction X. Utilisez la deuxième loi de rotation de Newton pour déterminer l'accélération angulaire.

    Solution
    Schéma d'un cylindre roulant et glissant le long d'un plan incliné et schéma du corps libre du cylindre. Sur la gauche se trouve une illustration du plan incliné, qui forme un angle thêta avec l'horizontale. Le cylindre est montré comme étant au repos en haut, puis se déplaçant le long de la pente lorsqu'il est plus bas. Sur la droite se trouve un schéma corporel gratuit. Le système de coordonnées x y est incliné de telle sorte que la direction x positive soit parallèle au plan incliné et pointe vers son bas, et que la direction y positive soit orientée vers l'extérieur, perpendiculaire au plan. Quatre forces sont présentées. N j hat agit au centre du cylindre et pointe dans la direction positive y. m g sine thêta i hat agit au centre du cylindre et pointe dans la direction positive x. Moins m g cosinus thêta j qui agit au centre du cylindre et pointe dans la direction négative y. Moins f sub k est ce qui agit au point de contact et pointe dans la direction x négative.
    Figure\(\PageIndex{6}\) : Un cylindre plein roule sur un plan incliné à partir du repos et glisse. Le système de coordonnées a x dans la direction descendante du plan incliné et y vers le haut perpendiculaire au plan. Le diagramme du corps libre montre la force normale, la force de friction cinétique et les composantes du poids\(\vec{g}\) m.

    La somme des forces dans la direction y étant nulle, la force de frottement est désormais de f k =\(\mu_{k}\) N =\(\mu_{k}\) mg cos\(\theta\). La deuxième loi de Newton dans la direction X devient

    \[\sum F_{x} = ma_{x}, \nonumber\]

    \[mg \sin \theta - \mu_{k} mg \cos \theta = m(a_{CM})_{x}, \nonumber\]

    ou

    \[(a_{CM})_{x} = g(\sin \theta - \mu_{k} \cos \theta) \ldotp \nonumber\]

    La force de friction fournit le seul couple autour de l'axe passant par le centre de gravité, de sorte que la deuxième loi de rotation de Newton devient

    \[\sum \tau_{CM} = I_{CM} \alpha, \nonumber\]

    \[f_{k} r = I_{CM} \alpha = \frac{1}{2} mr^{2} \alpha \ldotp \nonumber\]

    Pour résoudre ce problème\(\alpha\), nous avons

    \[\alpha = \frac{2f_{k}}{mr} = \frac{2 \mu_{k} g \cos \theta}{r} \ldotp \nonumber\]

    L'importance

    Nous écrivons les accélérations linéaires et angulaires en termes de coefficient de frottement cinétique. L'accélération linéaire est la même que celle trouvée pour un objet glissant sur un plan incliné avec friction cinétique. L'accélération angulaire autour de l'axe de rotation est linéairement proportionnelle à la force normale, qui dépend du cosinus de l'angle d'inclinaison. À\(\theta\) → 90°, cette force passe à zéro et, par conséquent, l'accélération angulaire passe à zéro.

    Conservation de l'énergie mécanique lors du mouvement de roulement

    Dans le chapitre précédent, nous avons introduit l'énergie cinétique de rotation. Tout objet roulant transporte de l'énergie cinétique de rotation, ainsi que de l'énergie cinétique de translation et de l'énergie potentielle si le système l'exige. En incluant l'énergie potentielle gravitationnelle, l'énergie mécanique totale d'un objet roulant est

    \[E_{T} = \frac{1}{2} mv^{2}_{CM} + \frac{1}{2} I_{CM} \omega^{2} + mgh \ldotp\]

    En l'absence de forces non conservatrices susceptibles d'extraire de l'énergie du système sous forme de chaleur, l'énergie totale d'un objet roulant sans glisser est conservée et est constante tout au long du mouvement. Parmi les exemples où l'énergie n'est pas conservée, citons un objet roulant qui glisse, la production de chaleur résultant du frottement cinétique et un objet roulant qui rencontre une résistance à l'air.

    Vous vous demandez peut-être pourquoi un objet roulant qui ne glisse pas économise de l'énergie, étant donné que la force de friction statique n'est pas conservatrice. La réponse peut être trouvée en se référant à la figure\(\PageIndex{2}\). Le point P en contact avec la surface est au repos par rapport à la surface. Son déplacement infinitésimal d par rapport\(\vec{r}\) à la surface est donc nul, et le travail incrémental effectué par la force de frottement statique est nul. Nous pouvons appliquer la conservation de l'énergie à notre étude du mouvement de roulement pour obtenir des résultats intéressants.

    Exemple\(\PageIndex{3}\): Curiosity Rover

    Le rover Curiosity, illustré à la figure\(\PageIndex{7}\), a été déployé sur Mars le 6 août 2012. Les roues du rover ont un rayon de 25 cm. Supposons que des astronautes arrivent sur Mars en 2050 et trouvent Curiosity, désormais inopérante, sur le bord d'un bassin. Pendant le démontage du rover, un astronaute perd accidentellement l'adhérence de l'une des roues, qui roule sans glisser dans le fond du bassin 25 mètres plus bas. Si la roue a une masse de 5 kg, quelle est sa vitesse au fond du bassin ?

    Une photographie du rover Curiosity de la NASA lors d'essais au Jet Propulsion Laboratory.
    Figure\(\PageIndex{7}\) : Le rover Curiosity du Mars Science Laboratory de la NASA lors d'essais le 3 juin 2011. L'emplacement se trouve à l'intérieur de l'installation d'assemblage de vaisseaux spatiaux du laboratoire de propulsion à réaction de la NASA à Pasadena, en Californie. (crédit : NASA/JPL-Caltech)

    Stratégie

    Nous utilisons la conservation de l'énergie mécanique pour analyser le problème. Au sommet de la colline, la roue est au repos et ne possède que de l'énergie potentielle. Au fond du bassin, la roue possède une énergie cinétique de rotation et de translation, qui doit être égale à l'énergie potentielle initiale par conservation d'énergie. Comme la roue roule sans glisser, nous utilisons la relation v CM = r\(\omega\) pour relier les variables de translation aux variables de rotation dans l'équation de conservation d'énergie. Nous résolvons ensuite la vitesse. Sur la figure\(\PageIndex{7}\), nous voyons qu'un cylindre creux est une bonne approximation de la roue, nous pouvons donc utiliser ce moment d'inertie pour simplifier le calcul.

    Solution

    L'énergie en haut du bassin est égale à l'énergie en bas :

    \[mgh = \frac{1}{2} mv_{CM}^{2} + \frac{1}{2} I_{CM} \omega^{2} \ldotp \nonumber\]

    Les quantités connues sont I CM = mr 2, r = 0,25 m et h = 25,0 m.

    Nous réécrivons l'équation de conservation d'énergie en\(\omega\) éliminant en utilisant\(\omega\) = v CM r. Nous avons

    \[mgh = \frac{1}{2} mv_{CM}^{2} + \frac{1}{2} mr^{2} \frac{v_{CM}^{2}}{r^{2}} \nonumber\]

    ou

    \[gh = \frac{1}{2} v_{CM}^{2} + \frac{1}{2} v_{CM}^{2} \Rightarrow v_{CM} = \sqrt{gh} \ldotp \nonumber\]

    Sur Mars, l'accélération de la gravité est de 3,71 m/s 2, ce qui donne l'amplitude de la vitesse au fond du bassin comme

    \[v_{CM} = \sqrt{(3.71\; m/s^{2})(25.0\; m)} = 9.63\; m/s \ldotp \nonumber\]

    L'importance

    Il s'agit d'un résultat assez précis étant donné que Mars possède très peu d'atmosphère et que la perte d'énergie due à la résistance de l'air serait minime. Le résultat suppose également que le terrain est lisse, de sorte que la roue ne rencontrerait pas de rochers et de bosses en cours de route.

    De plus, dans cet exemple, l'énergie cinétique, ou énergie du mouvement, est également partagée entre le mouvement linéaire et le mouvement de rotation. Si nous examinons les moments d'inertie de la Figure 10.5.4, nous voyons que le cylindre creux présente le moment d'inertie le plus important pour un rayon et une masse donnés. Si les roues du rover étaient solides et rapprochées par des cylindres pleins, par exemple, il y aurait plus d'énergie cinétique dans un mouvement linéaire que dans un mouvement de rotation. Cela donnerait à la roue une vitesse linéaire plus grande que l'approximation du cylindre creux. Ainsi, le cylindre plein atteindrait le fond du bassin plus rapidement que le cylindre creux.