10.6 : Calcul des moments d'inertie

Objectifs d'apprentissage

• Calculer le moment d'inertie pour des corps rigides de forme uniforme
• Appliquez le théorème de l'axe parallèle pour déterminer le moment d'inertie autour d'un axe parallèle à un axe déjà connu
• Calculer le moment d'inertie pour les objets composés

Dans la sous-section précédente, nous avons défini le moment d'inertie mais nous n'avons pas montré comment le calculer. Dans cette sous-section, nous montrons comment calculer le moment d'inertie pour plusieurs types d'objets standard, ainsi que comment utiliser les moments d'inertie connus pour déterminer le moment d'inertie d'un axe décalé ou d'un objet composé. Cette section est très utile pour découvrir comment appliquer une équation générale à des objets complexes (une compétence essentielle pour les cours de physique et d'ingénierie plus avancés).

Moment d'inertie

Nous avons défini le moment d'inertie I d'un objet comme étant

\[I = \sum_{i} m_i r_i^2 \]

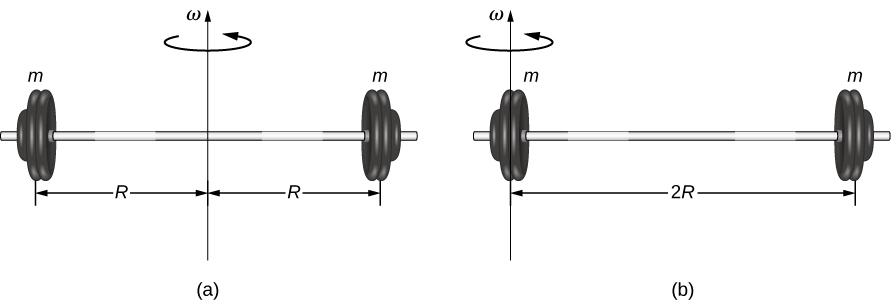
pour toutes les masses de points qui constituent l'objet. Comme\(r\) il s'agit de la distance par rapport à l'axe de rotation de chaque pièce de masse qui constitue l'objet, le moment d'inertie d'un objet dépend de l'axe choisi. Pour voir cela, prenons un exemple simple de deux masses au bout d'une tige sans masse (masse négligeable) (Figure\(\PageIndex{1}\)) et calculons le moment d'inertie autour de deux axes différents. Dans ce cas, la somme des masses est simple car les deux masses à la fin de la barre peuvent être approximées sous forme de masses ponctuelles, et la somme ne comporte donc que deux termes.

Dans le cas où l'axe est au centre de la barre, chacune des deux masses m est\(R\) éloignée de l'axe, ce qui donne un moment d'inertie de

\[I_{1} = mR^{2} + mR^{2} = 2mR^{2} \ldotp\]

Dans le cas où l'axe situé à l'extrémité de la barre traverse l'une des masses, le moment d'inertie est

\[I_{2} = m(0)^{2} + m(2R)^{2} = 4mR^{2} \ldotp\]

De ce résultat, nous pouvons conclure qu'il est deux fois plus difficile de faire pivoter la barre vers l'extrémité que vers son centre.

Figure\(\PageIndex{1}\) : (a) Une barre avec un axe de rotation passant par son centre ; (b) une haltère avec un axe de rotation passant par une extrémité.

Dans cet exemple, nous avions deux masses de points et la somme était simple à calculer. Cependant, pour traiter des objets qui ne ressemblent pas à des points, nous devons réfléchir soigneusement à chacun des termes de l'équation. L'équation nous demande de faire la somme sur chaque « pièce de masse » d'une certaine distance par rapport à l'axe de rotation. Mais que signifie exactement chaque « pièce de masse » ? Rappelons que dans notre dérivation de cette équation, chaque pièce de masse avait la même amplitude de vitesse, ce qui signifie que la pièce entière devait avoir une seule distance r par rapport à l'axe de rotation. Cependant, cela n'est pas possible à moins de prendre une masse infinitésimale dm, comme le montre la figure\(\PageIndex{2}\).

Figure\(\PageIndex{2}\) : Utilisation d'une masse infinitésimale pour calculer la contribution au moment d'inertie total.

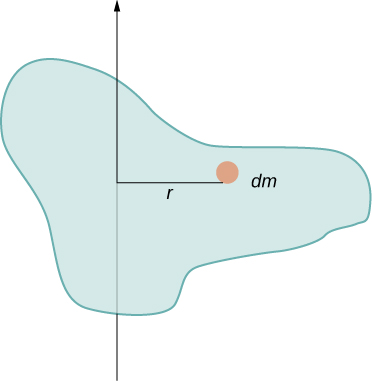
La nécessité d'utiliser une masse infinitésimale dm suggère que nous pouvons écrire le moment d'inertie en évaluant une intégrale sur des masses infinitésimales plutôt que de faire une somme discrète sur des masses finies :

\[I = \sum_{i} m_{i} r_{i}^{2}\]

devient

\[I = \int r^{2} dm \ldotp \label{10.19}\]

C'est en fait la forme dont nous avons besoin pour généraliser l'équation pour les formes complexes. Il est préférable d'élaborer des exemples spécifiques en détail pour avoir une idée de la manière de calculer le moment d'inertie pour des formes spécifiques. C'est l'objet de la majeure partie du reste de cette section.

Une tige mince uniforme avec un axe passant par le centre

Considérez une tige mince uniforme (densité et forme) de masse M et de longueur L, comme indiqué sur la figure\(\PageIndex{3}\). Nous voulons une tige fine afin de pouvoir supposer que la section transversale de la tige est petite et que la tige peut être considérée comme une chaîne de masses le long d'une ligne droite unidimensionnelle. Dans cet exemple, l'axe de rotation est perpendiculaire à la tige et passe par le point médian pour plus de simplicité. Notre tâche consiste à calculer le moment d'inertie autour de cet axe. Nous orientons les axes de manière à ce que l'axe z soit l'axe de rotation et que l'axe X passe par la longueur de la tige, comme indiqué sur la figure. C'est un choix pratique car nous pouvons ensuite intégrer le long de l'axe X.

Figure\(\PageIndex{3}\) : Calcul du moment d'inertie I pour une tige mince uniforme autour d'un axe passant par le centre de la tige.

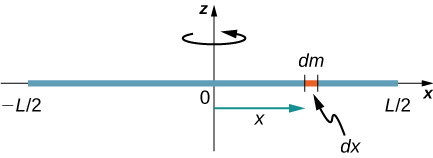
Nous définissons dm comme étant un petit élément de masse constituant la tige. L'intégrale du moment d'inertie est une intégrale de la distribution des masses. Cependant, nous savons comment nous intégrer dans l'espace et non dans la masse. Nous devons donc trouver un moyen de relier la masse aux variables spatiales. Pour ce faire, nous utilisons la densité\(\lambda\) de masse linéaire de l'objet, qui est la masse par unité de longueur. La densité de masse de cet objet étant uniforme, on peut écrire

\[\lambda = \frac{m}{l}\; or\; m = \lambda l \ldotp\]

Si nous prenons le différentiel de chaque côté de cette équation, nous trouvons

\[dm = d(\lambda l) = \lambda (dl)\]

puisque\(\lambda\) c'est constant. Nous avons choisi d'orienter la tige le long de l'axe X pour plus de commodité. C'est là que ce choix s'avère très utile. Notez qu'un morceau de la tige dl se trouve complètement le long de l'axe x et a une longueur dx ; en fait, dl = dx dans cette situation. Nous pouvons donc écrire dm =\(\lambda\) (dx), ce qui nous donne une variable d'intégration que nous savons gérer. La distance de chaque pièce de masse dm par rapport à l'axe est donnée par la variable x, comme indiqué sur la figure. En rassemblant tout cela, nous obtenons

\[I = \int r^{2} dm = \int x^{2} dm = \int x^{2} \lambda dx \ldotp\]

La dernière étape consiste à faire attention aux limites de notre intégration. La tige s'étend de x =\(− \frac{L}{2}\) à x =\(\frac{L}{2}\), puisque l'axe se trouve au milieu de la tige à x = 0. Cela nous donne

\[\begin{split} I & = \int_{- \frac{L}{2}}^{\frac{L}{2}} x^{2} \lambda dx = \lambda \frac{x^{3}}{3} \Bigg|_{- \frac{L}{2}}^{\frac{L}{2}} \\ & = \lambda \left(\dfrac{1}{3}\right) \Bigg[ \left(\dfrac{L}{2}\right)^{3} - \left(- \dfrac{L}{2}\right)^{3} \Bigg] = \lambda \left(\dfrac{1}{3}\right) \left(\dfrac{L^{3}}{8}\right) (2) = \left(\dfrac{M}{L}\right) \left(\dfrac{1}{3}\right) \left(\dfrac{L^{3}}{8}\right) (2) \\ & = \frac{1}{12} ML^{2} \ldotp \end{split}\]

Ensuite, nous calculons le moment d'inertie pour la même tige mince uniforme mais avec un choix d'axe différent afin de pouvoir comparer les résultats. On peut s'attendre à ce que le moment d'inertie soit plus petit autour d'un axe passant par le centre de gravité que autour de l'axe terminal, comme c'était le cas pour l'exemple des haltères au début de cette section. Cela se produit parce qu'une plus grande quantité de masse est distribuée plus loin de l'axe de rotation.

Une tige mince uniforme avec un axe à l'extrémité

Considérons maintenant la même tige mince uniforme de masse\(M\) et de longueur\(L\), mais cette fois, nous déplaçons l'axe de rotation jusqu'à l'extrémité de la tige. Nous souhaitons connaître le moment d'inertie autour de ce nouvel axe (Figure\(\PageIndex{4}\)).

Figure\(\PageIndex{4}\) : Calcul du moment d'inertie\(I\) pour une tige mince uniforme autour d'un axe passant par l'extrémité de la tige.

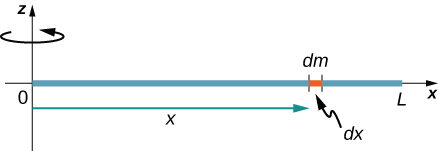
La quantité\(dm\) est à nouveau définie comme étant un petit élément de masse composant la tige. Comme auparavant, nous obtenons

\[I = \int r^{2} dm = \int x^{2} dm = \int x^{2} \lambda dx \ldotp\]

Cependant, cette fois-ci, nous avons des limites d'intégration différentes. La tige s'étend de\(x = 0\) à\(x = L\), puisque l'axe se trouve à l'extrémité de la tige à\(x = 0\). Par conséquent, nous trouvons

\[\begin{align} I & = \int_{0}^{L} x^{2} \lambda\, dx \\[4pt] &= \lambda \frac{x^{3}}{3} \Bigg|_{0}^{L} \\[4pt] &=\lambda \left(\dfrac{1}{3}\right) \Big[(L)^{3} - (0)^{3} \Big] \\[4pt] & = \lambda \left(\dfrac{1}{3}\right) L^{3} = \left(\dfrac{M}{L}\right) \left(\dfrac{1}{3}\right) L^{3} \\[4pt] &= \frac{1}{3} ML^{2} \ldotp \label{ThinRod} \end{align} \]

Notez que l'inertie de rotation de la tige autour de son extrémité est supérieure à l'inertie de rotation autour de son centre (conformément à l'exemple des haltères) d'un facteur quatre.

Le théorème de l'axe parallèle

La similitude entre le processus de détermination du moment d'inertie d'une tige autour d'un axe passant par son milieu et autour d'un axe passant par son extrémité est frappante et suggère qu'il pourrait exister une méthode plus simple pour déterminer le moment d'inertie d'une tige autour de n'importe quel axe parallèle à l'axe passant par le centre de masse. Un tel axe est appelé axe parallèle. Il existe un théorème pour cela, appelé théorème de l'axe parallèle, que nous énonçons ici mais dont nous ne dérivons pas dans ce texte.

Théorème de l'axe parallèle

Soit m la masse d'un objet et d la distance entre un axe passant par le centre de gravité de l'objet et un nouvel axe. Ensuite, nous avons

\[I_{\text{parallel-axis}} = I_{\text{center of mass}} + md^{2} \ldotp \label{10.20}\]

Appliquons ceci à la tige mince uniforme avec l'exemple d'axe résolu ci-dessus :

\[I_{parallel-axis} = I_{center\; of\; mass} + md^{2} = \frac{1}{12} mL^{2} + m \left(\dfrac{L}{2}\right)^{2} = \left(\dfrac{1}{12} + \dfrac{1}{4}\right) mL^{2} = \frac{1}{3} mL^{2} \ldotp\]

Ce résultat est conforme à notre calcul plus long (Equation \ ref {ThinRod}). L'équation \ ref {10.20} est une équation utile que nous appliquons dans certains exemples et problèmes.

Exercice\(\PageIndex{1}\)

Quel est le moment d'inertie d'un cylindre de rayon\(R\) et de masse\(m\) autour d'un axe passant par un point de la surface, comme indiqué ci-dessous ?

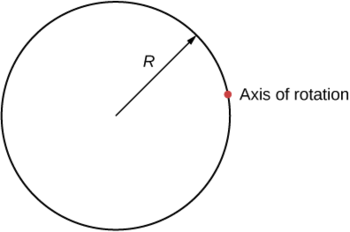
Réponse

\[I_{parallel-axis} = I_{center\; of\; mass} + md^{2} = mR^{2} + mR^{2} = 2mR^{2} \nonumber \]

Un disque mince uniforme autour d'un axe passant par le centre

L'intégration pour déterminer le moment d'inertie d'un objet bidimensionnel est un peu plus délicate, mais une forme est généralement réalisée à ce niveau d'étude : un disque mince uniforme autour d'un axe passant par son centre (Figure\(\PageIndex{5}\)).

Figure\(\PageIndex{5}\) : Calcul du moment d'inertie d'un disque mince autour d'un axe passant par son centre.

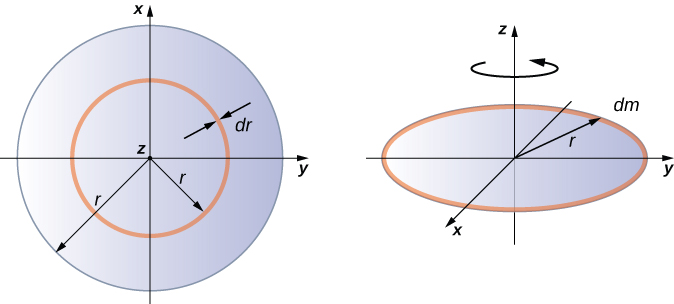
Comme le disque est mince, nous pouvons prendre la masse telle qu'elle est entièrement répartie dans le plan xy. Nous commençons à nouveau par la relation pour la densité de la masse surfacique, qui est la masse par unité de surface. Comme elle est uniforme, la masse volumique superficielle\(\sigma\) est constante :

\[\sigma = \frac{m}{A}\]ou\[\sigma A = m\] alors\[dm = \sigma (dA)\]

Nous utilisons maintenant une simplification pour la zone. La zone peut être considérée comme constituée d'une série d'anneaux fins, chaque anneau étant un incrément de masse dm de rayon\(r\) équidistant de l'axe, comme le montre la partie (b) de la figure. L'aire infinitésimale de chaque anneau\(dA\) est donc donnée par la longueur de chaque anneau (\(2 \pi r\)) multipliée par la largeur infinitésimale de chaque anneau\(dr\) :

\[A = \pi r^{2},\; dA = d(\pi r^{2}) = \pi dr^{2} = 2 \pi rdr \ldotp\]

La surface complète du disque est ensuite constituée en ajoutant tous les anneaux fins dont le rayon est compris entre\(0\) et\(R\). Cette plage de rayons devient alors notre limite d'intégration\(dr\), c'est-à-dire que nous intégrons de\(r = 0\) à\(r = R\). En rassemblant tout cela, nous avons

\[\begin{split} I & = \int_{0}^{R} r^{2} \sigma (2 \pi r) dr = 2 \pi \sigma \int_{0}^{R} r^{3} dr = 2 \pi \sigma \frac{r^{4}}{4} \Big|_{0}^{R} \\ & = 2 \pi \sigma \left(\dfrac{R^{4}}{4} - 0 \right) = 2 \pi \left(\dfrac{m}{A}\right) \left(\dfrac{R^{4}}{4}\right) = 2 \pi \left(\dfrac{m}{\pi R^{2}}\right) \left(\dfrac{R^{4}}{4}\right) = \frac{1}{2} mR^{2} \ldotp \end{split}\]

Notez que cela correspond à la valeur donnée dans la Figure 10.5.4.

Calcul du moment d'inertie pour des objets composés

Considérons maintenant un objet composé tel que celui de la figure\(\PageIndex{6}\), qui représente un disque fin au bout d'une fine tige. Cela ne peut pas être facilement intégré pour trouver le moment d'inertie car il ne s'agit pas d'un objet de forme uniforme. Cependant, si nous revenons à la définition initiale du moment d'inertie en tant que sommation, nous pouvons raisonner que le moment d'inertie d'un objet composé peut être trouvé à partir de la somme de chaque partie de l'objet :

\[I_{total} = \sum_{i} I_{i} \ldotp \label{10.21}\]

Il est important de noter que les moments d'inertie des objets dans l'équation\(\PageIndex{6}\) se situent autour d'un axe commun. Dans le cas de cet objet, il s'agirait d'une tige de longueur L tournant autour de son extrémité, et d'un mince disque de rayon\(R\) tournant autour d'un axe décalé du centre d'une distance\(L + R\), où\(R\) est le rayon du disque. Définissons la masse de la tige comme étant m _r et la masse du disque comme étant\(m_d\).

Figure\(\PageIndex{6}\) : Objet composé d'un disque au bout d'une tige. L'axe de rotation est situé à\(A\).

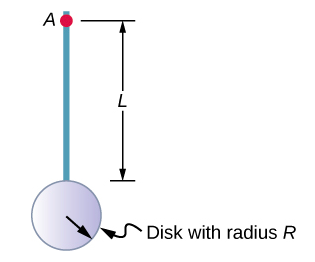
Le moment d'inertie de la tige est simple\(\frac{1}{3} m_rL^2\), mais il faut utiliser le théorème de l'axe parallèle pour déterminer le moment d'inertie du disque autour de l'axe représenté. Le moment d'inertie du disque autour de son centre est\(\frac{1}{2} m_dR^2\) et nous appliquons le théorème de l'axe parallèle (Équation \ ref {10.20}) pour trouver

\[I_{parallel-axis} = \frac{1}{2} m_{d} R^{2} + m_{d} (L + R)^{2} \ldotp\]

En ajoutant le moment d'inertie de la tige et le moment d'inertie du disque avec un axe de rotation décalé, nous trouvons que le moment d'inertie de l'objet composé est

\[I_{total} = \frac{1}{3} m_{r} L^{2} + \frac{1}{2} m_{d} R^{2} + m_{d} (L + R)^{2} \ldotp\]

Appliquer des calculs du moment d'inertie pour résoudre des problèmes

Examinons maintenant quelques applications pratiques des calculs des moments d'inertie.

Exemple\(\PageIndex{1}\): Person on a Merry-Go-Round

Un enfant de 25 kg se tient à\(r = 1.0\, m\) distance de l'axe d'un manège rotatif (Figure\(\PageIndex{7}\)). Le manège peut être assimilé à un disque solide uniforme d'une masse de 500 kg et d'un rayon de 2,0 m. Déterminez le moment d'inertie de ce système.

Figure\(\PageIndex{7}\) : Calcul du moment d'inertie d'un enfant lors d'un manège.

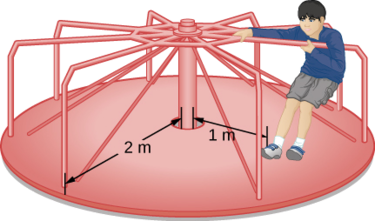
Stratégie

Ce problème implique le calcul d'un moment d'inertie. On nous donne la masse et la distance par rapport à l'axe de rotation de l'enfant ainsi que la masse et le rayon du manège. Comme la masse et la taille de l'enfant sont beaucoup plus petites que celles du manège, nous pouvons approximer l'enfant sous la forme d'une masse ponctuelle. La notation que nous utilisons est m _c = 25 kg, r _c = 1,0 m, m _m = 500 kg, r _m = 2,0 m. Notre objectif est de trouver\(I_{total} = \sum_{i} I_{i}\) (Équation \ ref {10.21}).

Solution

Pour l'enfant\(I_c = m_cr^2\), et pour le manège,\(I_m = \frac{1}{2}m_m r^2\). Par conséquent

\[I_{total} = 25(1)^{2} + \frac{1}{2} (500)(2)^{2} = 25 + 1000 = 1025\; kg\; \cdotp m^{2} \ldotp \nonumber \]

L'importance

La valeur doit être proche du moment d'inertie du manège en lui-même, car la masse de ce manège est beaucoup plus importante que celle de l'enfant.

Exemple\(\PageIndex{2}\): Rod and Solid Sphere

Déterminez le moment d'inertie de la combinaison tige et sphère solide autour des deux axes, comme indiqué ci-dessous. La tige a une longueur de 0,5 m et une masse de 2,0 kg. Le rayon de la sphère est de 20,0 cm et a une masse de 1,0 kg.

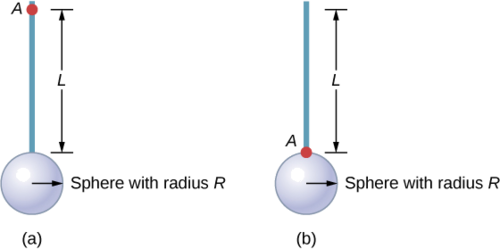
Stratégie

Comme nous avons un objet composé dans les deux cas, nous pouvons utiliser le théorème des axes parallèles pour déterminer le moment d'inertie autour de chaque axe. Dans (a), le centre de gravité de la sphère est situé à distance\(L + R\) de l'axe de rotation. Dans (b), le centre de gravité de la sphère est situé à une certaine\(R\) distance de l'axe de rotation. Dans les deux cas, le moment d'inertie de la tige se situe autour d'un axe situé à une extrémité. Reportez-vous au Tableau 10.4 pour les moments d'inertie des objets individuels.

un.

\[\begin{split} I_{total} & = \sum_{i} I_{i} = I_{Rod} + I_{Sphere}; \\ I_{Sphere} & = I_{center\; of\; mass} + m_{Sphere} (L + R)^{2} = \frac{2}{5} m_{Sphere} R^{2} + m_{Sphere} (L + R)^{2}; \\ I_{total} & = I_{Rod} + I_{Sphere} = \frac{1}{3} m_{Rod} L^{2} + \frac{2}{5} m_{Sphere} R^{2} + m_{Sphere} (L + R)^{2}; \\ I_{total} & = \frac{1}{3} (20\; kg)(0.5\; m)^{2} + \frac{2}{5} (1.0\; kg)(0.2\; m)^{2} + (1.0\; kg)(0.5\; m + 0.2\; m)^{2}; \\ I_{total} & = (0.167 + 0.016 + 0.490)\; kg\; \cdotp m^{2} = 0.673\; kg\; \cdotp m^{2} \ldotp \end{split}\]

b.

\[\begin{split} I_{Sphere} & = \frac{2}{5} m_{Sphere} R^{2} + m_{Sphere} R^{2}; \\ I_{total} & = I_{Rod} + I_{Sphere} = \frac{1}{3} m_{Rod} L^{2} + \frac{2}{5} (1.0\; kg)(0.2\; m)^{2} + (1.0\; kg)(0.2\; m)^{2}; \\ I_{total} & = (0.167 + 0.016 + 0.04)\; kg\; \cdotp m^{2} = 0.223\; kg\; \cdotp m^{2} \ldotp \end{split}\]

L'importance

L'utilisation du théorème de l'axe parallèle facilite le calcul du moment d'inertie des objets composés. Nous voyons que le moment d'inertie est plus grand en (a) qu'en (b). En effet, l'axe de rotation est plus proche du centre de masse du système en (b). La simple analogie est celle d'une canne. Le moment d'inertie autour d'une extrémité est\(\frac{1}{3}\) mL ², mais le moment d'inertie à travers le centre de masse sur toute sa longueur est\(\frac{1}{12}\) mL ².

Exemple\(\PageIndex{3}\): Angular Velocity of a Pendulum

Un pendule en forme de tige (Figure\(\PageIndex{8}\)) est libéré du repos sous un angle de 30°. Il a une longueur de 30 cm et une masse de 300 g. Quelle est sa vitesse angulaire à son point le plus bas ?

Figure\(\PageIndex{8}\) : Un pendule en forme de tige est libéré du repos à un angle de 30°.

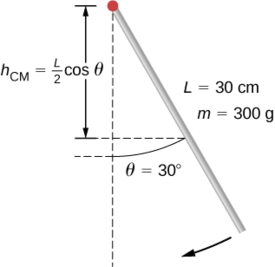
Stratégie

Utilisez les économies d'énergie pour résoudre le problème. Au point de déclenchement, le pendule possède une énergie potentielle gravitationnelle, qui est déterminée à partir de la hauteur du centre de gravité au-dessus de son point le plus bas dans la balançoire. Au bas de la balançoire, toute l'énergie potentielle gravitationnelle est convertie en énergie cinétique de rotation.

Solution

La variation de l'énergie potentielle est égale à la variation de l'énergie cinétique de rotation,\(\Delta U + \Delta K = 0\).

Au sommet de la balançoire :

\[U = mgh_{cm} = mgL^2 (\cos \theta). \nonumber \]

Au bas de la balançoire,

\[U = mg \frac{L}{2}. \nonumber\]

Au sommet du swing, l'énergie cinétique de rotation est K = 0. Au bas de la balançoire, K =\(\frac{1}{2} I \omega^{2}\). Par conséquent :

\[\Delta U + \Delta K = 0 \Rightarrow (mg \frac{L}{2} (1 - \cos \theta) - 0) + (0 - \frac{1}{2} I \omega^{2}) = 0 \nonumber\]

ou

\[\frac{1}{2} I \omega^{2} = mg \frac{L}{2} (1 - \cos \theta) \ldotp \nonumber\]

Pour résoudre ce problème\(\omega\), nous avons

\[\omega = \sqrt{mg \frac{L}{I} (1 - \cos \theta)} = \sqrt{mg \frac{L}{\frac{1}{3} mL^{2}} (1 - \cos \theta)} = \sqrt{g \frac{3}{L} (1 - \cos \theta)} \ldotp \nonumber\]

En insérant des valeurs numériques, nous avons

\[\omega = \sqrt{(9.8\; m/s^{2}) \left(\dfrac{3}{0.3\; m}\right) (1 - \cos 30)} = 3.6\; rad/s \ldotp \nonumber\]

L'importance

Notez que la vitesse angulaire du pendule ne dépend pas de sa masse.