10.5 : Moment d'inertie et énergie cinétique de rotation
- Page ID
- 191439
- Décrire les différences entre l'énergie cinétique de rotation et de translation
- Définir le concept physique du moment d'inertie en termes de distribution de la masse à partir de l'axe de rotation
- Expliquer comment le moment d'inertie des corps rigides affecte leur énergie cinétique de rotation
- Utiliser la conservation de l'énergie mécanique pour analyser les systèmes soumis à la fois à la rotation et à
- Calculer la vitesse angulaire d'un système rotatif lorsqu'il y a des pertes d'énergie dues à des forces non conservatrices
Jusqu'à présent, dans ce chapitre, nous avons travaillé sur la cinématique de rotation : la description du mouvement d'un corps rigide rotatif avec un axe de rotation fixe. Dans cette section, nous définissons deux nouvelles grandeurs utiles pour analyser les propriétés des objets en rotation : le moment d'inertie et l'énergie cinétique de rotation. Une fois ces propriétés définies, nous disposerons de deux outils importants dont nous aurons besoin pour analyser la dynamique de rotation.
Énergie cinétique de rotation
Tout objet en mouvement possède de l'énergie cinétique. Nous savons comment le calculer pour un corps soumis à un mouvement de translation, mais qu'en est-il pour un corps rigide en rotation ? Cela peut sembler compliqué car chaque point du corps rigide a une vitesse différente. Cependant, nous pouvons utiliser la vitesse angulaire, qui est la même pour l'ensemble du corps rigide, pour exprimer l'énergie cinétique d'un objet en rotation. La figure\(\PageIndex{1}\) montre un exemple de corps rotatif très énergique : une meule électrique propulsée par un moteur. Des étincelles volent et du bruit et des vibrations sont générés lorsque la meule fait son travail. Ce système possède une énergie considérable, dont une partie sous forme de chaleur, de lumière, de son et de vibrations. Cependant, la majeure partie de cette énergie se présente sous forme d'énergie cinétique de rotation.
L'énergie dans le mouvement de rotation n'est pas une nouvelle forme d'énergie ; il s'agit plutôt de l'énergie associée au mouvement de rotation, de la même manière que l'énergie cinétique dans le mouvement de translation. Cependant, étant donné que l'énergie cinétique est donnée par\(K=\frac{1}{2}mv^2\) et que la vitesse est une quantité différente pour chaque point d'un corps rotatif autour d'un axe, il est logique de trouver un moyen d'écrire l'énergie cinétique en termes de variable\(\omega\), qui est la même pour tous les points d'un corps rotatif rigide. Pour une seule particule tournant autour d'un axe fixe, cela est simple à calculer. Nous pouvons relier la vitesse angulaire à l'amplitude de la vitesse de translation en utilisant la relation\(v_t=\omega r\), où\(r\) est la distance de la particule par rapport à l'axe de rotation et\(v_t\) sa vitesse tangentielle. En remplaçant l'énergie cinétique dans l'équation, nous trouvons
\[ K=\frac{1}{2} m v_{t}^{2}=\frac{1}{2} m(\omega r)^{2}=\frac{1}{2}\left(m r^{2}\right) \omega^{2}. \nonumber \]
Dans le cas d'un corps rotatif rigide, nous pouvons diviser n'importe quel corps en un grand nombre de masses plus petites, chacune ayant une masse\(m_j\) et une distance par rapport à l'axe de rotation\(r_j\), de telle sorte que la masse totale du corps soit égale à la somme des masses individuelles :\(M=\sum_{j} m_{j}\). Chaque plus petite masse a une vitesse tangentielle\(v_j\), où nous avons abandonné l'indice\(t\) pour le moment. L'énergie cinétique totale du corps rotatif rigide est
\[ K=\sum_{j} \frac{1}{2} m_{j} v_{j}^{2}=\sum_{j} \frac{1}{2} m_{j}\left(r_{j} \omega_{j}\right)^{2} \nonumber \]
et puisque\(\omega_j = \omega\) pour toutes les masses,
\[ K=\frac{1}{2}\left(\sum_{j} m_{j} r_{j}^{2}\right) \omega^{2} . \label{10.16} \]
Les unités de l'équation \ ref {10.16} sont les joules (J). L'équation sous cette forme est complète, mais maladroite ; nous devons trouver un moyen de la généraliser.
Moment d'inertie
Si nous comparons l'équation \ ref {10.16} à la façon dont nous avons écrit l'énergie cinétique dans Travail et Énergie cinétique, (\(\frac{1}{2}mv^2\)), cela suggère que nous avons une nouvelle variable rotationnelle à ajouter à notre liste de relations entre les variables rotationnelles et translationnelles. La quantité\(\sum_{j} m_{j} r_{j}^{2}\) est la contrepartie de la masse dans l'équation de l'énergie cinétique de rotation. Il s'agit d'un nouveau terme important pour désigner le mouvement de rotation. Cette quantité est appelée moment d'inertie\(I\), avec des unités de kg·m 2 :
\[ I=\sum_{j} m_{j} r_{j}^{2} . \label{10.17} \]
Pour l'instant, nous laissons l'expression sous forme de sommation, représentant le moment d'inertie d'un système de particules ponctuelles tournant autour d'un axe fixe. Nous remarquons que le moment d'inertie d'une particule ponctuelle unique autour d'un axe fixe est simplement\(mr^2\) la distance entre la particule\(r\) ponctuelle et l'axe de rotation. Dans la section suivante, nous explorons la forme intégrale de cette équation, qui peut être utilisée pour calculer le moment d'inertie de certains corps rigides de forme régulière.
Le moment d'inertie est la mesure quantitative de l'inertie rotationnelle, tout comme dans le mouvement de translation, et la masse est la mesure quantitative de l'inertie linéaire, c'est-à-dire que plus un objet est massif, plus il possède d'inertie et plus sa résistance au changement de vitesse linéaire est grande. De même, plus le moment d'inertie d'un corps rigide ou d'un système de particules est élevé, plus sa résistance au changement de vitesse angulaire autour d'un axe de rotation fixe est grande. Il est intéressant de voir comment le moment d'inertie varie avec r, la distance par rapport à l'axe de rotation des particules de masse dans l'équation \ ref {10.17}. Les corps rigides et les systèmes de particules dont la masse est plus concentrée à une plus grande distance de l'axe de rotation ont des moments d'inertie supérieurs à ceux des corps et des systèmes de même masse, mais concentrés près de l'axe de rotation. De cette façon, nous pouvons voir qu'un cylindre creux a plus d'inertie rotationnelle qu'un cylindre plein de même masse lorsqu'il tourne autour d'un axe passant par le centre. En remplaçant l'équation \ ref {10.17} par l'équation \ ref {10.16}, l'expression de l'énergie cinétique d'un corps rigide en rotation devient
\[ K=\frac{1}{2} I \omega^{2} . \label{10.18} \]
Cette équation montre que l'énergie cinétique d'un corps rigide en rotation est directement proportionnelle au moment d'inertie et au carré de la vitesse angulaire. Ceci est exploité dans les dispositifs de stockage d'énergie à volant, conçus pour stocker de grandes quantités d'énergie cinétique de rotation. De nombreux constructeurs automobiles testent actuellement des dispositifs de stockage d'énergie du volant d'inertie dans leurs automobiles, tels que le volant ou le système de récupération d'énergie cinétique, illustré à la figure\(\PageIndex{2}\).

Les grandeurs rotationnelles et translationnelles pour l'énergie cinétique et l'inertie sont résumées dans le tableau 10.4. La colonne des relations n'est pas incluse car il n'existe pas de constante par laquelle nous pourrions multiplier la quantité rotationnelle pour obtenir la quantité translationnelle, comme cela peut être fait pour les variables du tableau 10.3.
| Rotationnel | Translationnel |
|---|---|
| \(I=\sum_{j} m_{j} r_{j}^{2}\) | \(m\) |
| \(K = \frac{1}{2}I \omega^2\) | \(K = \frac{1}{2} m v^2 \) |
Six petites rondelles sont espacées de 10 cm sur une tige de masse négligeable et de 0,5 m de long. La masse de chaque rondelle est de 20 g. La tige tourne autour d'un axe situé à 25 cm, comme indiqué sur la figure\(\PageIndex{3}\). a) Quel est le moment d'inertie du système ? (b) Si les deux rondelles les plus proches de l'axe sont retirées, quel est le moment d'inertie des quatre rondelles restantes ? (c) Si le système à six rondelles tourne à 5 tr/min, quelle est son énergie cinétique de rotation ?
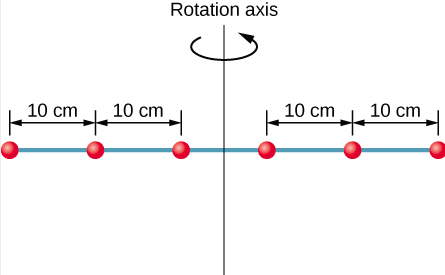
Stratégie
- Nous utilisons la définition du moment d'inertie pour un système de particules et effectuons la sommation pour évaluer cette quantité. Les masses sont toutes les mêmes, nous pouvons donc placer cette quantité devant le symbole de sommation.
- Nous faisons un calcul similaire.
- Nous insérons le résultat de (a) dans l'expression de l'énergie cinétique de rotation.
Solution
- \(I=\sum m_{j} r_{j}^{2}=(0.02 \: \mathrm{kg})\left(2 \times(0.25 \: \mathrm{m})^{2}+2 \times(0.15 \: \mathrm{m})^{2}+2 \times(0.05 \: \mathrm{m})^{2}\right)=0.0035 \: \mathrm{kg} \cdot \mathrm{m}^{2}\)
- \(I=\sum_{j} m_{j} r_{j}^{2}=(0.02 \: \mathrm{kg})\left(2 \times(0.25 \: \mathrm{m})^{2}+2 \times(0.15 \: \mathrm{m})^{2}\right)=0.0034 \: \mathrm{kg} \cdot \mathrm{m}^{2}\)
- \(K=\frac{1}{2} I \omega^{2}=\frac{1}{2}\left(0.0035 \: \mathrm{kg} \cdot \mathrm{m}^{2}\right)(5.0 \times 2 \pi \: \mathrm{rad} / \mathrm{s})^{2}=1.73 \: \mathrm{J}\)
L'importance
Nous pouvons voir les contributions individuelles au moment d'inertie. Les masses proches de l'axe de rotation ont une très faible contribution. Lorsque nous les avons retirés, cela n'a eu qu'un très faible effet sur le moment d'inertie.
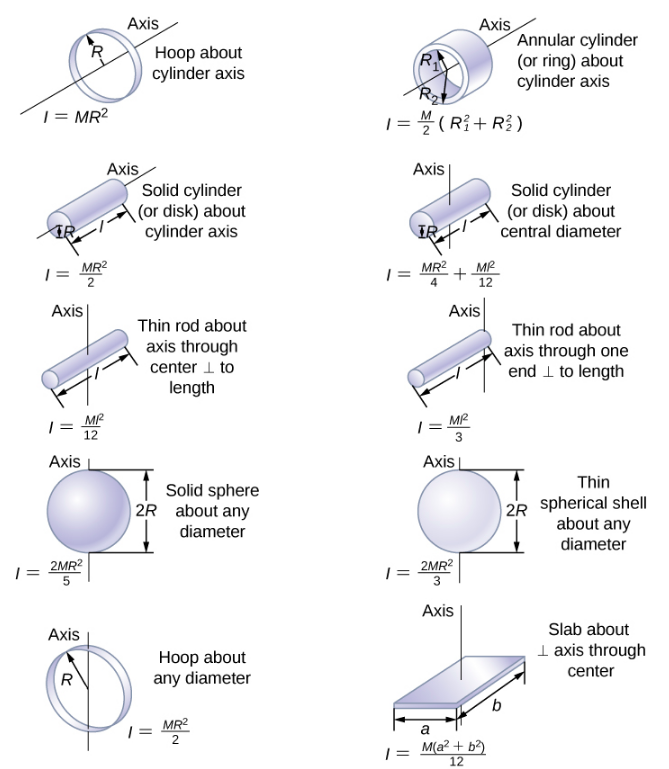
Dans la section suivante, nous généralisons l'équation de sommation pour les particules ponctuelles et développons une méthode pour calculer les moments d'inertie pour les corps rigides. Pour l'instant, cependant, la figure\(\PageIndex{4}\) donne des valeurs d'inertie rotationnelle pour les formes d'objets courantes autour d'axes spécifiés.
Application de l'énergie cinétique de rotation
Appliquons maintenant les idées de l'énergie cinétique de rotation et de la table des moments d'inertie pour avoir une idée de l'énergie associée à la rotation de quelques objets. Les exemples suivants vous aideront également à vous familiariser avec ces équations. Examinons d'abord une stratégie générale de résolution des problèmes liés à l'énergie de rotation.
- Déterminez si la rotation implique de l'énergie ou du travail.
- Déterminez le système qui vous intéresse. Un croquis est généralement utile.
- Analysez la situation afin de déterminer les types de travail et d'énergie nécessaires.
- S'il n'y a pas de pertes d'énergie dues au frottement et à d'autres forces non conservatrices, l'énergie mécanique est conservée, c'est-à-dire\(K_i + U_i = K_f + U_f\).
- Si des forces non conservatrices sont présentes, l'énergie mécanique n'est pas conservée et d'autres formes d'énergie, telles que la chaleur et la lumière, peuvent entrer dans le système ou en sortir. Déterminez ce qu'ils sont et calculez-les si nécessaire.
- Éliminez les termes dans la mesure du possible pour simplifier l'algèbre.
- Évaluez la solution numérique pour voir si elle est logique compte tenu de la situation physique présentée dans la formulation du problème.
Un petit hélicoptère de sauvetage type possède quatre pales : chacune mesure 4 m de long et a une masse de 50 kg (Figure\(\PageIndex{5}\)). Les lames peuvent être assimilées à de fines tiges qui tournent autour d'une extrémité d'un axe perpendiculaire à leur longueur. La masse totale en charge de l'hélicoptère est de 1 000 kg. (a) Calculez l'énergie cinétique de rotation des pales lorsqu'elles tournent à 300 tr/min. (b) Calculez l'énergie cinétique de translation de l'hélicoptère lorsqu'il vole à 20,0 m/s et comparez-la à l'énergie de rotation des pales.

Stratégie
Les énergies cinétiques de rotation et de translation peuvent être calculées à partir de leurs définitions. La formulation du problème donne toutes les constantes nécessaires pour évaluer les expressions des énergies cinétiques de rotation et de translation.
Solution
a. L'énergie cinétique de rotation est
\[ K = \frac{1}{2} I \omega^2 \nonumber \]
Nous devons convertir la vitesse angulaire en radians par seconde et calculer le moment d'inertie avant de pouvoir la trouver\(K\). La vitesse angulaire\(\omega\) est
\[ \omega=\frac{300 \text { rev }}{1.00 \min } \frac{2 \pi \text { rad }}{1 \text { rev }} \frac{1.00 \: \min }{60.0 \: \mathrm{s}}=31.4 \: \frac{\mathrm{rad}}{\mathrm{s}}. \nonumber \]
Le moment d'inertie d'une lame est celui d'une fine tige tournée autour de son extrémité, indiqué sur la figure\(\PageIndex{4}\). Le total\(I\) est quatre fois ce moment d'inertie car il y a quatre pales. Ainsi,
\[ I=4 \frac{M l^{2}}{3}=4 \times \frac{(50.0 \: \mathrm{kg})(4.00 \: \mathrm{m})^{2}}{3}=1067.0 \: \mathrm{kg} \cdot \mathrm{m}^{2} \nonumber .\]
Entrer\(\omega\) et\(I\) entrer dans l'expression de l'énergie cinétique de rotation donne
\[ K=0.5\left(1067 \: \mathrm{kg} \cdot \mathrm{m}^{2}\right)(31.4 \: \mathrm{rad} / \mathrm{s})^{2}=5.26 \times 10^{5} \: \mathrm{J}. \nonumber \]
b. En entrant les valeurs données dans l'équation de l'énergie cinétique translationnelle, nous obtenons
\[ K=\frac{1}{2} m v^{2}=(0.5)(1000.0 \: \mathrm{kg})(20.0 \: \mathrm{m} / \mathrm{s})^{2}=2.00 \times 10^{5} \: \mathrm{J} . \nonumber \]
Pour comparer les énergies cinétiques, nous prenons le rapport entre l'énergie cinétique de translation et l'énergie cinétique de rotation. Ce ratio est
\[ \frac{2.00 \times 10^{5} \: \mathrm{J}}{5.26 \times 10^{5} \: \mathrm{J}}=0.380 . \nonumber \]
L'importance
Le rapport entre l'énergie de translation et l'énergie cinétique de rotation n'est que de 0,380. Ce ratio nous indique que la majeure partie de l'énergie cinétique de l'hélicoptère se trouve dans ses pales qui tournent.
Une personne lance un boomerang en l'air à une vitesse de 30,0 m/s sous un angle de 40,0° par rapport à l'horizontale (Figure\(\PageIndex{6}\)). Il a une masse de 1,0 kg et tourne à 10,0 tr/min. Le moment d'inertie du boomerang est donné comme\(I=\frac{1}{12} m L^{2} \) suit\(L\) : 0,7 m. (a) Quelle est l'énergie totale du boomerang lorsqu'il quitte la main ? (b) Quelle est la hauteur du boomerang par rapport à l'élévation de la main, sans tenir compte de la résistance à l'air ?
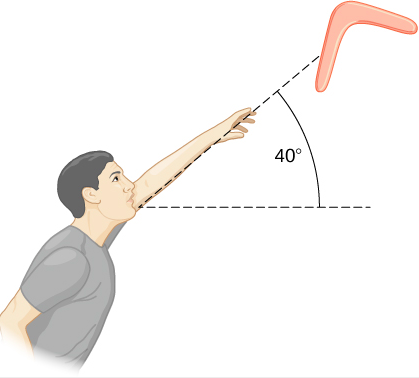
Stratégie
Nous utilisons les définitions de l'énergie cinétique de rotation et de l'énergie cinétique linéaire pour déterminer l'énergie totale du système. Le problème consiste à négliger la résistance à l'air, de sorte que nous n'avons pas à nous soucier de la perte d'énergie. Dans la partie (b), nous utilisons la conservation de l'énergie mécanique pour déterminer la hauteur maximale du boomerang.
Solution
a. Moment d'inertie :\( I=\frac{1}{12} m L^{2}=\frac{1}{12}(1.0 \: \mathrm{kg})(0.7 \: \mathrm{m})^{2}=0.041 \: \mathrm{kg} \cdot \mathrm{m}^{2}. \)
Vitesse angulaire :\( \omega=(10.0 \: \mathrm{rev} / \mathrm{s})(2 \pi)=62.83 \: \mathrm{rad} / \mathrm{s} \)
L'énergie cinétique de rotation est donc
\[ K_{R}=\frac{1}{2}\left(0.041 \: \mathrm{kg} \cdot \mathrm{m}^{2}\right)(62.83 \: \mathrm{rad} / \mathrm{s})^{2}=80.93 \: \mathrm{J} \nonumber \]
L'énergie cinétique de translation est
\[ K_{\mathrm{T}}=\frac{1}{2} m v^{2}=\frac{1}{2}(1.0 \: \mathrm{kg})(30.0 \: \mathrm{m} / \mathrm{s})^{2}=450.0 \: \mathrm{J} \nonumber \]
Ainsi, l'énergie totale du boomerang est
\[ K_{\text {Total }}=K_{R}+K_{T}=80.93+450.0=530.93 \: \mathrm{J}. \nonumber \]
b. Nous utilisons la conservation de l'énergie mécanique. Comme le boomerang est lancé à un angle, nous devons écrire les énergies totales du système en termes d'énergies cinétiques linéaires en utilisant la vitesse dans les directions x et y. L'énergie totale lorsque le boomerang quitte la main est
\[ E_{\text {Before }}=\frac{1}{2} m v_{x}^{2}+\frac{1}{2} m v_{y}^{2}+\frac{1}{2} I \omega^{2} \nonumber \]
L'énergie totale à la hauteur maximale est
\[ E_{\text {Final }}=\frac{1}{2} m v_{x}^{2}+\frac{1}{2} I \omega^{2}+m g h \nonumber \]
En économisant l'énergie mécanique, nous avons\(E_{Before} = E_{Final}\) donc, après avoir annulé des conditions similaires,
\[ \frac{1}{2} m v_{y}^{2}=m g h \nonumber .\]
Puisque\(v_y\) = 30,0 m/s (\(\sin 40^{\circ}\)) = 19,28 m/s, on trouve
\[ h=\frac{(19.28 \: \mathrm{m} / \mathrm{s})^{2}}{2\left(9.8 \: \mathrm{m} / \mathrm{s}^{2}\right)}=18.97 \: \mathrm{m} \nonumber \]
L'importance
Dans la partie (b), la solution montre comment la conservation de l'énergie est une méthode alternative pour résoudre un problème qui serait normalement résolu par la cinématique. En l'absence de résistance à l'air, l'énergie cinétique de rotation n'a pas joué un rôle dans la solution pour la hauteur maximale.
Une hélice de sous-marin nucléaire a un moment d'inertie de 800,0 kg • m 2. Si l'hélice immergée a une vitesse de rotation de 4,0 tr/min lorsque le moteur est coupé, quelle est la vitesse de rotation de l'hélice après 5,0 s lorsque la résistance à l'eau a retiré 50 000 J du système ?


