6.5 : Friction (partie 2)
- Page ID
- 191607
Le frottement et le plan incliné
Une situation dans laquelle la friction joue un rôle évident est celle d'un objet sur une pente. Il peut s'agir d'une caisse poussée sur une rampe menant à un quai de chargement ou d'un skateur dévalant une montagne, mais la physique de base est la même. Nous généralisons généralement la surface inclinée et l'appelons plan incliné, puis nous prétendons que la surface est plate. Regardons un exemple d'analyse du mouvement sur un plan incliné avec friction.
Un skieur pesant 62 kg glisse sur une pente enneigée à vitesse constante. Détermine le coefficient de friction cinétique du skieur si l'on sait que la friction est de 45,0 N.
Stratégie
L'amplitude de la friction cinétique est donnée par 45,0 N. La friction cinétique est liée à la force normale N par f k =\(\mu_{k}\) N ; ainsi, nous pouvons déterminer le coefficient de frottement cinétique si nous pouvons trouver la force normale sur le skieur. La force normale est toujours perpendiculaire à la surface et, comme il n'y a aucun mouvement perpendiculaire à la surface, la force normale doit être égale à la composante du poids du skieur perpendiculaire à la pente. (Voir Figure\(\PageIndex{1}\), qui reprend une figure du chapitre sur les lois du mouvement de Newton.)
Nous avons
\[N = w_{y} = w \cos 25^{o} = mg \cos 25^{o} \ldotp\]
En substituant cela à notre expression de friction cinétique, nous obtenons
\[f_{k} = \mu_{k} mg \cos 25^{o},\]
qui peut maintenant être résolu pour le coefficient de frottement cinétique\(\mu_{k}\).
Solution
Résoudre pour\(\mu_{k}\) donner
\[\mu_{k} = \frac{f_{k}}{N} = \frac{f_{k}}{w \cos 25^{o}} = \frac{f_{k}}{mg \cos 25^{o}} \ldotp\]
En substituant des valeurs connues sur le côté droit de l'équation,
\[\mu_{k} = \frac{45.0\; N}{(62\; kg)(9.80\; m/s^{2})(0.906)} = 0.082 \ldotp\]
L'importance
Ce résultat est légèrement inférieur au coefficient indiqué dans le tableau 6.1 pour le bois ciré sur neige, mais il reste raisonnable car les valeurs des coefficients de frottement peuvent varier considérablement. Dans de telles situations, où un objet de masse m glisse le long d'une pente formant un angle\(\theta\) avec l'horizontale, le frottement est donné par f k =\(\mu_{k}\) mg cos\(\theta\). Tous les objets glissent le long d'une pente avec une accélération constante dans ces circonstances.
Nous avons discuté du fait que lorsqu'un objet repose sur une surface horizontale, la force normale qui le soutient est égale en amplitude à son poids. De plus, le simple frottement est toujours proportionnel à la force normale. Lorsqu'un objet ne se trouve pas sur une surface horizontale, comme c'est le cas pour le plan incliné, il faut déterminer la force agissant sur l'objet qui est dirigée perpendiculairement à la surface ; elle est une composante du poids.
Nous dérivons maintenant une relation utile pour calculer le coefficient de frottement sur un plan incliné. Notez que le résultat ne s'applique qu'aux situations dans lesquelles l'objet glisse à vitesse constante sur la rampe.
Un objet glisse sur un plan incliné à une vitesse constante si la force nette exercée sur l'objet est nulle. Nous pouvons utiliser ce fait pour mesurer le coefficient de friction cinétique entre deux objets. Comme le montre l'exemple\(\PageIndex{1}\), le frottement cinétique sur une pente est f k =\(\mu_{k}\) mg cos\(\theta\). La composante du poids en bas de la pente est égale à mg sin\(\theta\) (voir le diagramme du corps libre sur la figure\(\PageIndex{1}\)). Ces forces agissent dans des directions opposées, donc lorsqu'elles ont la même amplitude, l'accélération est nulle. En les écrivant,
\[\mu_{k} mg \cos \theta = mg \sin \theta \ldotp\]
En résolvant pour\(\mu_{k}\), nous constatons que
\[\mu_{k} = \frac{mg \sin \theta}{mg \cos \theta} = \tan \theta \ldotp\]
Placez une pièce sur un livre et inclinez-la jusqu'à ce que la pièce glisse à vitesse constante le long du livre. Il se peut que vous deviez toucher légèrement le livre pour faire bouger la pièce. Mesurez l'angle d'inclinaison par rapport à l'horizontale et trouvez\(\mu_{k}\). Notez que la pièce ne commence à glisser que lorsqu'un angle supérieur\(\theta\) à celui atteint, car le coefficient de frottement statique est supérieur au coefficient de frottement cinétique. Réfléchissez à la manière dont cela peut affecter la valeur\(\mu_{k}\) et son incertitude.
Explications de la friction à l'échelle atomique
Les aspects les plus simples de la friction traités jusqu'à présent sont ses caractéristiques macroscopiques (à grande échelle). De grands progrès ont été réalisés dans l'explication à l'échelle atomique de la friction au cours des dernières décennies. Les chercheurs découvrent que la nature atomique du frottement semble présenter plusieurs caractéristiques fondamentales. Ces caractéristiques expliquent non seulement certains des aspects les plus simples de la friction, mais elles offrent également le potentiel de développement d'environnements pratiquement exempts de friction qui pourraient permettre d'économiser des centaines de milliards de dollars en énergie qui est actuellement convertie (inutilement) en chaleur.
La figure\(\PageIndex{2}\) illustre une caractéristique macroscopique du frottement expliquée par des recherches microscopiques (à petite échelle). Nous avons remarqué que le frottement est proportionnel à la force normale, mais pas à la surface de contact, une notion quelque peu contre-intuitive. Lorsque deux surfaces rugueuses sont en contact, la surface de contact réelle ne représente qu'une infime fraction de la surface totale, car seuls les points élevés se touchent. Lorsqu'une force normale plus importante est exercée, la surface de contact réelle augmente et nous constatons que le frottement est proportionnel à cette zone.
Cependant, la vue à l'échelle atomique promet d'expliquer bien plus que les simples caractéristiques de la friction. Le mécanisme de production de chaleur est en cours de détermination. En d'autres termes, pourquoi les surfaces chauffent-elles lorsqu'elles sont frottées ? Essentiellement, les atomes sont liés les uns aux autres pour former des réseaux. Lorsque les surfaces frottent, les atomes de surface adhèrent et font vibrer les réseaux atomiques, créant essentiellement des ondes sonores qui pénètrent dans le matériau. Les ondes sonores diminuent avec la distance et leur énergie est convertie en chaleur. Des réactions chimiques liées à l'usure par friction peuvent également se produire entre les atomes et les molécules présentes sur les surfaces. La figure\(\PageIndex{3}\) montre comment la pointe d'une sonde tracée sur un autre matériau est déformée par un frottement à l'échelle atomique. La force nécessaire pour faire glisser la pointe peut être mesurée et s'avère liée à la contrainte de cisaillement, qui est abordée dans Equilibre statique et élasticité. La variation de la contrainte de cisaillement est remarquable (plus d'un facteur 1012) et difficile à prévoir théoriquement, mais la contrainte de cisaillement permet de mieux comprendre un phénomène à grande échelle connu depuis l'Antiquité : la friction.
Décrivez un modèle de friction au niveau moléculaire. Décrivez la matière en termes de mouvement moléculaire. La description doit inclure des diagrammes à l'appui de la description ; comment la température affecte l'image ; quelles sont les différences et les similitudes entre le mouvement des particules solides, liquides et gazeuses ; et comment la taille et la vitesse des molécules de gaz sont liées aux objets du quotidien.
Les deux blocs de Figure\(\PageIndex{4}\) sont attachés l'un à l'autre par une ficelle sans masse enroulée autour d'une poulie sans friction. Lorsque le bloc inférieur de 4,00 kg est tiré vers la gauche par une force constante\(\vec{P}\), le bloc supérieur de 2 kg glisse dessus vers la droite. Détermine l'amplitude de la force nécessaire pour déplacer les blocs à vitesse constante. Supposons que le coefficient de frottement cinétique entre toutes les surfaces est de 0,400.
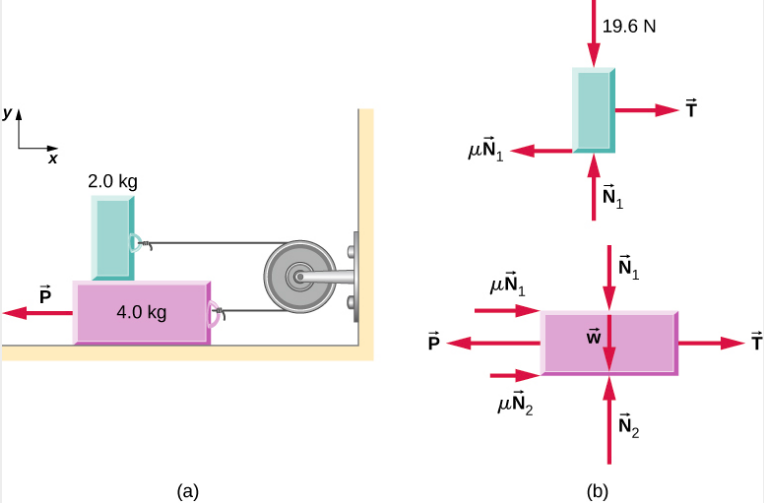
Stratégie
Nous analysons les mouvements des deux blocs séparément. Le bloc supérieur est soumis à une force de contact exercée par le bloc inférieur. Les composantes de cette force sont la force normale N 1 et la force de frottement −0,400 N 1. Les autres forces qui s'exercent sur le bloc supérieur sont la tension T de la corde et le poids du bloc supérieur lui-même, 19,6 N. Le bloc inférieur est soumis à des forces de contact dues au bloc supérieur et au sol. La première force de contact comporte des composantes -N 1 et 0,400 N 1, qui sont simplement des forces de réaction aux forces de contact que le bloc inférieur exerce sur le bloc supérieur. Les composantes de la force de contact du sol sont N 2 et 0,400 N 2. Les autres forces qui s'exercent sur ce bloc sont −P, la tension T et le poids —39,2 N. Solution Comme le bloc supérieur se déplace horizontalement vers la droite à vitesse constante, son accélération est nulle dans les directions horizontale et verticale. À partir de la deuxième loi de Newton,
|
\[\sum F_{x} = m_{2} a_{x}\] \[T - 0.400\; N_{1} = 0\] |
\[\sum F_{y} = m_{1} a_{y}\] \[N_{1} - 19.6\; N = 0 \ldotp\] |
En résolvant les deux inconnues, nous obtenons N 1 = 19,6 N et T = 0,40 N 1 = 7,84 N. Le bloc inférieur n'accélère pas non plus, de sorte que l'application de la deuxième loi de Newton à ce bloc donne
|
\[\sum F_{x} = m_{2} a_{x}\] \[T - P + 0.400\; N_{1} + 0.400\; N_{2} = 0\] |
\[\sum F_{y} = m_{1} a_{y}\] \[N_{2} - 39.2\; N - N_{1} = 0 \ldotp\] |
Les valeurs de N 1 et T ont été trouvées avec le premier ensemble d'équations. Lorsque ces valeurs sont substituées dans le deuxième ensemble d'équations, nous pouvons déterminer N 2 et P. Ils sont
\[N_{2} = 58.8\; N\; and\; P = 39.2\; N \ldotp\]
L'importance
Il est souvent difficile de comprendre dans quelle direction puiser la force de friction. Notez que chaque force de friction indiquée sur la figure\(\PageIndex{4}\) agit dans la direction opposée au mouvement du bloc correspondant.
Une caisse de 50 kg repose sur la plate-forme d'un camion, comme le montre la figure\(\PageIndex{5}\). Les coefficients de frottement entre les surfaces sont\(\mu_{k}\) = 0,300 et\(\mu_{s}\) = 0,400. Déterminez la force de frottement exercée sur la caisse lorsque le camion accélère vers l'avant par rapport au sol à (a) 2,00 m/s 2 et (b) à 5,00 m/s 2.
Stratégie
Les forces exercées sur la caisse sont son poids et les forces normales et de friction dues au contact avec la plate-forme du camion. Nous partons du principe que la caisse ne glisse pas. Dans ce cas, la force de frottement statique fs agit sur la caisse. De plus, les accélérations de la caisse et du camion sont égales.
Solution
- L'application de la deuxième loi de Newton à la caisse, à l'aide du référentiel fixé au sol, donne
\[\begin{split} \sum F_{x} & = ma_{x} \\ f_{s} & = (50.0\; kg)(2.00\; m/s^{2}) \\ & = 1.00 \times 10^{2}\; N \end{split}\]
\[\begin{split} \sum F_{y} & = ma_{y} \\ N - 4.90 \times 10^{2}\; N & = (50.0\; kg)(0) \\ N & = 4.90 \times 10^{2}\; N \ldotp \end{split}\]
Nous pouvons maintenant vérifier la validité de notre hypothèse antidérapante. La valeur maximale de la force de friction statique est $$ \ mu_ {s} N = (0,400) (4,90 \ times 10^ {2} \ ; N) = 196 \ ; N, $$ alors que la force réelle de friction statique qui agit lorsque le camion accélère vers l'avant à 2,00 m/s 2 n'est que de 1,00 x 10 2 N. Ainsi, l'hypothèse d'absence de glissement est valide.
- Si la caisse doit se déplacer avec le camion lorsqu'il accélère à 5,0 m/s 2, la force de friction statique doit être $$f_ {s} = ma_ {x} = (50,0 \ ; kg) (5,00 \ ; m/s^ {2}) = 250 \ ; N \ LDotp$$$ Puisque cette valeur dépasse le maximum de 196 N, la caisse doit glisser. La force de frottement est donc cinétique et est de $$f_ {k} = \ mu_ {k} N = (0,300) (4,90 \ times 10^ {2} \ ; N) = 147 \ ; N \ LDotp$$$L'accélération horizontale de la caisse par rapport au sol se trouve maintenant à partir de $$ \ begin {split} \ sum F_ {x} & = ma_ {x} \ 147 \ 147 \ ; N & = (50,0 \ ; kg) a_ {x}, \ \ donc \ ; a_ {x} & = 2,94 \ ; m/s ^ {2} \ ldotp \ end {split} \]
L'importance
Par rapport au sol, le camion accélère vers l'avant à 5,0 m/s 2 et la caisse accélère vers l'avant à 2,94 m/s 2. La caisse glisse donc vers l'arrière par rapport à la caisse du camion avec une accélération de 2,94 m/s 2 − 5,00 m/s 2 = −2,06 m/s 2.
Plus tôt, nous avons analysé la situation d'un skieur alpin se déplaçant à vitesse constante afin de déterminer le coefficient de friction cinétique. Faisons maintenant une analyse similaire pour déterminer l'accélération. Le snowboardeur de Figure\(\PageIndex{6}\) glisse sur une pente inclinée de\(\theta\) = 13° par rapport à l'horizontale. Le coefficient de frottement cinétique entre la planche et la neige est\(\mu_{k}\) = 0,20. Quelle est l'accélération du snowboardeur ?
Stratégie
Les forces qui agissent sur le snowboardeur sont son poids et la force de contact de la pente, qui possède une composante normale à l'inclinaison et une composante le long de l'inclinaison (force de friction cinétique). Comme elle se déplace le long de la pente, le cadre de référence le plus pratique pour analyser son mouvement est celui où l'axe X est le long et l'axe y perpendiculaire à l'inclinaison. Dans ce cadre, les forces normales et les forces de frottement se situent le long des axes de coordonnées, les composantes du poids sont mg sin θ le long de la pente et mg cos\(\theta\) à angle droit dans la pente, et la seule accélération se situe le long de l'axe des abscisses (a y = 0).
Solution
Nous pouvons désormais appliquer la deuxième loi de Newton au snowboardeur :
|
\[\begin{split} \sum F_{x} & = ma_{x} \\ mg \sin \theta - \mu_{k} N & = ma_{x} \end{split}\] |
\[\begin{split} \sum F_{y} & = ma_{y} \\ N - mg \cos \theta &= m(0) \ldotp \end{split}\] |
À partir de la deuxième équation, N = mg cos\(\theta\). En substituant cela dans la première équation, nous trouvons
\[\begin{split} a_{x} & = g(\sin \theta - \mu_{k} \cos \theta) \\ & = g(\sin 13^{o} - 0.520 \cos 13^{o}) = 0.29\; m/s^{2} \ldotp \end{split}\]
L'importance
Remarquez à partir de cette équation que si elle\(\theta\)\(\mu_{k}\) est suffisamment petite ou assez grande, un x est négatif, c'est-à-dire que le snowboardeur ralentit.
Le snowboardeur descend maintenant une colline avec une pente de 10,0°. Quelle est l'accélération du skieur ?


