2.5 : Systèmes de coordonnées et composants d'un vecteur (Partie 2)
- Page ID
- 191255
Coordonnées polaires
Pour décrire les emplacements de points ou de vecteurs dans un plan, nous avons besoin de deux directions orthogonales. Dans le système de coordonnées cartésien, ces directions sont données par des vecteurs unitaires\(\hat{i}\) et\(\hat{j}\) le long de l'axe des abscisses et des ordonnées, respectivement. Le système de coordonnées cartésien est très pratique à utiliser pour décrire les déplacements et les vitesses des objets et les forces qui s'exercent sur eux. Cependant, cela devient fastidieux lorsqu'il s'agit de décrire la rotation d'objets. Lorsque nous décrivons la rotation, nous travaillons généralement dans le système de coordonnées polaires.
Dans le système de coordonnées polaires, la position du point P dans un plan est donnée par deux coordonnées polaires (Figure\(\PageIndex{1}\)). La première coordonnée polaire est la coordonnée radiale r, qui est la distance entre le point P et l'origine. La deuxième coordonnée polaire est un angle\(\varphi\) que le vecteur radial fait avec une direction choisie, généralement la direction X positive. En coordonnées polaires, les angles sont mesurés en radians, ou rads. Le vecteur radial est attaché à l'origine et pointe à distance de l'origine jusqu'au point P. Cette direction radiale est décrite par un vecteur radial unitaire\(\hat{r}\). Le second vecteur unitaire\(\hat{t}\) est un vecteur orthogonal à la direction radiale\(\hat{r}\). La\(\hat{t}\) direction positive + indique la façon dont l'angle\(\varphi\) change dans le sens antihoraire. Ainsi, un point P qui possède des coordonnées (x, y) dans le système rectangulaire peut être décrit de manière équivalente dans le système de coordonnées polaires par les deux coordonnées polaires (r,\(\varphi\)). L'équation 2.4.13 est valide pour n'importe quel vecteur, nous pouvons donc l'utiliser pour exprimer les coordonnées x et y du vecteur\(\vec{r}\). De cette façon, nous obtenons la connexion entre les coordonnées polaires et les coordonnées rectangulaires du point P :
\[ \begin{cases} x = r \cos \varphi \\ y = r \sin \varphi \end{cases} \ldotp \label{2.18}\]
Un chasseur de trésors trouve une pièce d'argent à 20,0 m d'un puits sec dans la direction 20° nord-est et trouve une pièce d'or à 10,0 m du puits dans la direction 20° nord-ouest. Quelles sont les coordonnées polaires et rectangulaires de ces résultats par rapport au puits ?
Stratégie
Le puits indique l'origine du système de coordonnées et l'est correspond à la direction +x. Nous déterminons les distances radiales entre les emplacements et l'origine, qui sont r S = 20,0 m (pour la pièce d'argent) et r G = 10,0 m (pour la pièce d'or). Pour trouver les coordonnées angulaires, on convertit 20° en radians : 20° =\(\frac{\pi\; 20}{180}\) =\(\frac{\pi}{9}\). Nous utilisons l'équation \ ref {2.18} pour trouver les coordonnées x et y des pièces.
Solution
La coordonnée angulaire de la pièce d'argent est\(\varphi_{S}\) =\(\frac{\pi}{9}\), tandis que la coordonnée angulaire de la pièce d'or est\(\varphi_{G}\) =\(\pi\) −\(\frac{\pi}{9}\) =\(\frac{8 \pi}{9}\). Ainsi, les coordonnées polaires de la pièce d'argent sont (r S,\(\varphi_{S}\)) = (20,0 m,\(\frac{\pi}{9}\)) et celles de la pièce d'or sont (r G,\(\varphi_{G}\)) = (10,0 m, \ frac {8 \ pi} {9} \)). Nous substituons ces coordonnées dans l'équation \ ref {2.18} pour obtenir des coordonnées rectangulaires. Pour la pièce d'or, les coordonnées sont
\[ \begin{cases} x_{G} = r_{G} \cos \varphi_{G} = (10.0\; m) \cos \frac{8 \pi}{9} = -9.4\; m \\ y_{G} = r_{G} \sin \varphi_{G} = (10.0\; m) \sin \frac{8 \pi}{9} = 3.4\; m \end{cases} \Rightarrow (x_{G}, y_{G}) = (-9.4\; m, 3.4\; m) \ldotp\]
Pour la pièce d'argent, les coordonnées sont
\[ \begin{cases} x_{S} = r_{S} \cos \varphi_{S} = (20.0\; m) \cos \frac{\pi}{9} = 18.9\; m \\ y_{S} = r_{S} \sin \varphi_{S} = (20.0\; m) \sin \frac{\pi}{9} = 6.8\; m \end{cases} \Rightarrow (x_{S}, y_{S}) = (18.9\; m, 6.8\; m) \ldotp\]
Vecteurs en trois dimensions
Pour spécifier l'emplacement d'un point dans l'espace, nous avons besoin de trois coordonnées (x, y, z), où les coordonnées x et y indiquent des emplacements dans un plan et la coordonnée z donne des positions verticales au-dessus ou en dessous du plan. L'espace tridimensionnel possède trois directions orthogonales, nous n'avons donc pas besoin de deux mais de trois vecteurs unitaires pour définir un système de coordonnées tridimensionnel. Dans le système de coordonnées cartésien, les deux premiers vecteurs unitaires sont le vecteur unitaire de l'axe des\(\hat{i}\) abscisses et le vecteur unitaire de l'axe des\(\hat{j}\) y. Le troisième vecteur unitaire\(\hat{k}\) est la direction de l'axe Z (Figure\(\PageIndex{2}\)). L'ordre dans lequel les axes sont étiquetés, c'est-à-dire l'ordre dans lequel les trois vecteurs unitaires apparaissent, est important car il définit l'orientation du système de coordonnées. L'ordre x-y-z, qui est équivalent à l'ordre\(\hat{i}\)\(\hat{j}\) -\(\hat{k}\), définit le système de coordonnées standard pour droitiers (orientation positive).
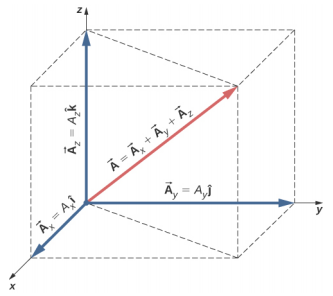
Dans l'espace tridimensionnel, le vecteur\(\vec{A}\) comporte trois composantes vectorielles : la composante x\(\vec{A}_{x}\) = A x\(\hat{i}\), qui est la partie du vecteur\(\vec{A}\) le long de l'axe x ; la composante y\(\vec{A}_{y}\) = A y\(\hat{j}\), qui est la partie le\(\vec{A}\) long de l'axe y- axe ; et la composante z\(\vec{A}_{z}\) = A z\(\hat{k}\), qui est la partie du vecteur le long de l'axe Z. Un vecteur dans un espace tridimensionnel est la somme vectorielle de ses trois composantes vectorielles (Figure\(\PageIndex{3}\)) :
\[\vec{A} = A_{x} \hat{i} + A_{y} \hat{j} + A_{z} \hat{k} \ldotp \label{2.19}\]
Si l'on connaît les coordonnées de son origine b (x b, y b, z b) et de son extrémité e (x e y e, z e), ses composantes scalaires sont obtenues en prenant leurs différences : A x et A y sont donnés par
\[ \begin{cases} A_{x} = x_{e} - x_{b} \nonumber \\ A_{y} = y_{e} - y_{b} \ldotp \nonumber \end{cases} \]
et la composante z est donnée par
\[A_{z} = z_{e} - z_{b} \ldotp \label{2.20}\]
La magnitude A est obtenue en généralisant l'équation 2.4.8 à trois dimensions :
\[A = \sqrt{A_{x}^{2} + A_{y}^{2} + A_{z}^{2}} \ldotp \label{2.21}\]
Cette expression de la magnitude du vecteur provient de l'application à deux reprises du théorème de Pythagore. Comme le montre la figure\(\PageIndex{3}\), la diagonale dans le plan xy a une longueur\(\sqrt{A_{x}^{2} + A_{y}^{2}}\) et son carré s'ajoute au carré A z 2 pour donner A 2. Notez que lorsque la composante z est nulle, le vecteur se trouve entièrement dans le plan xy et sa description est réduite à deux dimensions.
Lors du décollage de l'IAI Heron (Figure\(\PageIndex{4}\)), sa position par rapport à une tour de contrôle est de 100 m au-dessus du sol, à 300 m à l'est et à 200 m au nord. Une minute plus tard, il se trouve à 250 m au-dessus du sol, à 1200 m à l'est et à 2100 m au nord. Quel est le vecteur de déplacement du drone par rapport à la tour de contrôle ? Quelle est l'ampleur de son vecteur de déplacement ?
Stratégie
Nous prenons l'origine du système de coordonnées cartésien comme tour de contrôle. La direction de l'axe+x est donnée par un vecteur unitaire\(\hat{i}\) vers l'est, la direction de l'axe+y est donnée par un vecteur unitaire\(\hat{j}\) vers le nord et la direction de l'axe+z est donnée par un vecteur unitaire\(\hat{k}\), qui pointe vers le haut depuis le sol. La première position du drone est l'origine (ou, de manière équivalente, le début) du vecteur de déplacement et sa seconde position est la fin du vecteur de déplacement.
Solution
Nous identifions b (300,0 m, 200,0 m, 100,0 m) et e (480,0 m, 370,0 m, 250,0 m), et utilisons l'équation 2.4.4 et l'équation \ ref {2.20} pour trouver les composantes scalaires du vecteur de déplacement du drone :
\[ \begin{cases} D_{x} = x_{e} - x_{b} = 1200.0\; m - 300.0\; m = 900.0\; m,\\ D_{y} =y_{e} - y_{b} = 2100.0\; m - 200.0\; m = 1900.0\; m, \\ D_{z} =z_{e} - z_{b} = 250.0\; m - 100.0\; m = 150\; m \ldotp \end{cases}\]
Nous substituons ces composantes dans l'équation \ ref {2.19} pour trouver le vecteur de déplacement :
\[\vec{D} = D_{x}\; \hat{i} + D_{y}\; \hat{j} + D_{z}\; \hat{k} = 900.0\; \hat{i} + 1900.0\; \hat{j} + 150.0\; \hat{k} = (0.90\; \hat{i} + 1.90\; \hat{j} + 0.15\; \hat{k})\; km \ldotp\]
Nous la substituons dans l'équation \ ref {2.21} pour trouver l'amplitude du déplacement :
\[D = \sqrt{D_{x}^{2} + D_{y}^{2} + D_{z}^{2}} = \sqrt{(0.90\; km)^{2} + (1.90\; km)^{2} + (0.15\; km)^{2}} = 4.44\; km \ldotp\]
Si le vecteur de vitesse moyenne du drone dans le déplacement de l'exemple 2.7 est\(\vec{u}\) = (15,0\(\hat{i}\) + 31,7\(\hat{j}\) + 2,5\(\hat{k}\)) m/s, quelle est l'amplitude du vecteur de vitesse du drone ?


