2.3 : Scalaires et vecteurs (partie 2)

Exemple\(\PageIndex{1}\): A Ladybug Walker

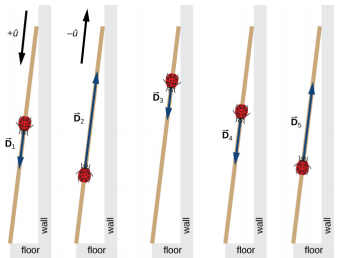
Un long bâton de mesure repose contre un mur dans un laboratoire de physique et son extrémité de 200 cm se trouve au sol. Une coccinelle atterrit sur la barre des 100 cm et rampe au hasard le long du bâton. Il marche d'abord 15 cm vers le sol, puis 56 cm vers le mur, puis il marche à nouveau 3 cm vers le sol. Puis, après un bref arrêt, il continue sur 25 cm vers le sol, puis, de nouveau, il remonte à 19 cm vers le mur avant de s'immobiliser complètement (Figure\(\PageIndex{1}\)). Trouvez le vecteur de son déplacement total et de sa position finale de repos sur le bâton.

Stratégie

Si nous choisissons la direction le long du bâton vers le sol comme direction du vecteur unitaire\(\hat{u}\), alors la direction vers le sol est\(+ \hat{u}\) et la direction vers le mur est\(−\hat{u}\). La coccinelle effectue au total cinq déplacements :

\[ \begin{align*} \vec{D}_{1} &= (15\; cm)( + \hat{u}), \\[4pt] \vec{D}_{2} &= (56\; cm)( - \hat{u}), \\[4pt] \vec{D}_{3} &= (3\; cm)( + \hat{u}), \\[4pt] \vec{D}_{4} &= (25\; cm)( + \hat{u}), \; and \\[4pt] \vec{D}_{5} &= (19\; cm)( - \hat{u}) \ldotp \end{align*}\]

Le déplacement total\(\vec{D}\) est la résultante de tous ses vecteurs de déplacement.

Figure\(\PageIndex{1}\) : Cinq déplacements de la coccinelle. Notez que dans ce dessin schématique, les magnitudes des déplacements ne sont pas tracées à l'échelle. (crédit : modification de l'œuvre de « Persian Poet Gal » /Wikimedia Commons)

Solution

La résultante de tous les vecteurs de déplacement est

\[ \begin{align*} \vec{D} &= \vec{D}_{1} + \vec{D}_{2} + \vec{D}_{3} + \vec{D}_{4} + \vec{D}_{5} \\[4pt] &= (15\; cm)( + \hat{u} ) + (56\; cm)( −\hat{u} ) + (3\; cm)( + \hat{u} ) + (25\; cm)( + \hat{u}) + (19\; cm)( − \hat{u}) \\[4pt] &= (15 − 56 + 3 + 25 − 19) cm\; \hat{u} \\[4pt] &= −32\; cm\; \hat{u} \ldotp \end{align*}\]

Dans ce calcul, nous utilisons la loi distributive donnée par l'équation 2.2.9. Le résultat indique que le vecteur de déplacement total s'éloigne de la marque des 100 cm (site d'atterrissage initial) vers l'extrémité de la barre de mesure qui touche le mur. L'extrémité qui touche le mur est marquée de 0 cm, de sorte que la position finale de la coccinelle se situe entre 100 et 32 cm = 68 cm.

Exercice 2.2

Un plongeur pénètre dans un long tunnel sous-marin. Lorsque son déplacement par rapport au point d'entrée est de 20 m, elle laisse tomber accidentellement son appareil photo, mais elle ne remarque qu'il a disparu avant d'être à environ 6 m plus loin dans le tunnel. Elle recule de 10 m à la nage mais ne trouve pas la caméra, elle décide donc de mettre fin à la plongée. À quelle distance se trouve-t-elle du point d'entrée ? En prenant la direction positive hors du tunnel, quel est son vecteur de déplacement par rapport au point d'entrée ?

Algèbre des vecteurs en deux dimensions

Lorsque les vecteurs se trouvent dans un plan, c'est-à-dire lorsqu'ils sont en deux dimensions, ils peuvent être multipliés par des scalaires, ajoutés à d'autres vecteurs ou soustraits d'autres vecteurs conformément aux lois générales exprimées par l'équation 2.2.1, l'équation 2.2.2, l'équation 2.2.7, et Équation 2.2.8. Cependant, la règle d'addition pour deux vecteurs dans un plan devient plus compliquée que la règle pour l'ajout de vecteurs dans une dimension. Nous devons utiliser les lois de la géométrie pour construire les vecteurs résultants, suivies de la trigonométrie pour déterminer les magnitudes et les directions des vecteurs. Cette approche géométrique est couramment utilisée en navigation (Figure\(\PageIndex{2}\)). Dans cette section, nous devons avoir à portée de main deux règles, un triangle, un rapporteur, un crayon et une gomme pour dessiner des vecteurs à l'échelle selon des constructions géométriques.

Figure\(\PageIndex{2}\) : En navigation, les lois de la géométrie sont utilisées pour dessiner les déplacements résultants sur des cartes marines.

Pour une construction géométrique de la somme de deux vecteurs dans un plan, nous suivons la règle du parallélogramme. Supposons que deux vecteurs\(\vec{A}\)\(\vec{B}\) se trouvent aux positions arbitraires illustrées sur la figure\(\PageIndex{3}\). Traduisez l'un ou l'autre d'entre eux en parallèle au début de l'autre vecteur, de sorte qu'après la traduction, les deux vecteurs aient leur origine au même point. Maintenant, à la fin du vecteur,\(\vec{A}\) nous dessinons une ligne parallèle au vecteur\(\vec{B}\) et à la fin du vecteur,\(\vec{B}\) nous dessinons une ligne parallèle au vecteur\(\vec{A}\) (les lignes pointillées sur la figure\(\PageIndex{3}\)). De cette façon, on obtient un parallélogramme. À partir de l'origine des deux vecteurs, nous dessinons une diagonale qui est la résultante\(\vec{R}\) des deux vecteurs :\(\vec{R}\) =\(\vec{A}\) +\(\vec{B}\) (Figure\(\PageIndex{3a}\)). L'autre diagonale de ce parallélogramme est la différence vectorielle des deux vecteurs\(\vec{D}\) =\(\vec{A}\) −\(\vec{B}\), comme le montre la figure\(\PageIndex{3b}\). Notez que la fin du vecteur de différence est placée à la fin du vecteur\(\vec{A}\).

Figure\(\PageIndex{3}\) : La règle du parallélogramme pour l'ajout de deux vecteurs. Effectuez la translation parallèle de chaque vecteur jusqu'à ce que leurs origines (marquées par un point) coïncident et construisez un parallélogramme avec deux côtés sur les vecteurs et les deux autres côtés (indiqués par des lignes pointillées) parallèles aux vecteurs. (a) Tracez le vecteur résultant\(\vec{R}\) le long de la diagonale du parallélogramme, du point commun au coin opposé. La longueur R du vecteur résultant n'est pas égale à la somme des magnitudes des deux vecteurs. (b) Tracez le vecteur de différence\(\vec{D}\) =\(\vec{A}\) −\(\vec{B}\) le long de la diagonale reliant les extrémités des vecteurs. Placez l'origine du vecteur\(\vec{D}\) à la fin du vecteur\(\vec{B}\) et la fin (pointe de flèche) du vecteur\(\vec{D}\) à la fin du vecteur\(\vec{A}\). La longueur D du vecteur de différence n'est pas égale à la différence de magnitudes des deux vecteurs.

Il découle de la règle du parallélogramme que ni l'amplitude du vecteur résultant ni l'amplitude du vecteur de différence ne peuvent être exprimées sous la forme d'une simple somme ou d'une différence des grandeurs A et B, car la longueur d'une diagonale ne peut pas être exprimée sous la forme d'une simple somme de longueurs latérales. Lorsque nous utilisons une construction géométrique pour déterminer les magnitudes |\(\vec{R}\) | et |\(\vec{D}\) |, nous devons utiliser les lois de trigonométrie pour les triangles, ce qui peut conduire à une algèbre complexe. Il existe deux manières de contourner cette complexité algébrique. L'une des solutions consiste à utiliser la méthode des composants, que nous examinerons dans la section suivante. L'autre méthode consiste à dessiner les vecteurs à l'échelle, comme c'est le cas pour la navigation, et à lire les longueurs et les angles (directions) approximatifs des vecteurs à partir des graphiques. Dans cette section, nous examinons la deuxième approche.

Si nous devons ajouter trois vecteurs ou plus, nous répétons la règle du parallélogramme pour les paires de vecteurs jusqu'à ce que nous trouvions la résultante de toutes les résultantes. Pour trois vecteurs, par exemple, nous trouvons d'abord la résultante du vecteur 1 et du vecteur 2, puis nous trouvons la résultante de cette résultante et du vecteur 3. L'ordre dans lequel nous sélectionnons les paires de vecteurs n'a pas d'importance car l'opération d'addition de vecteurs est commutative et associative (voir Équation 2.2.7 et Équation 2.2.8). Avant d'énoncer une règle générale qui découle des applications répétitives de la règle du parallélogramme, examinons l'exemple suivant.

Supposons que vous planifiez un voyage de vacances en Floride. Au départ de Tallahassee, la capitale de l'État, vous prévoyez de rendre visite à votre oncle Joe à Jacksonville, de voir votre cousin Vinny à Daytona Beach, de vous arrêter pour vous amuser un peu à Orlando, d'assister à un spectacle de cirque à Tampa et de visiter l'université de Floride à Gainesville. Votre itinéraire peut être représenté par cinq vecteurs de déplacement\(\vec{A}\)\(\vec{B}\),\(\vec{C}\),\(\vec{D}\), et\(\vec{E}\), qui sont indiqués par les vecteurs rouges sur la figure\(\PageIndex{4}\). Quel est votre déplacement total lorsque vous atteignez Gainesville ? Le déplacement total est la somme vectorielle des cinq vecteurs de déplacement, qui peut être trouvée en utilisant la règle du parallélogramme quatre fois. Vous pouvez également vous rappeler que le vecteur de déplacement commence à la position initiale (Tallahassee) et se termine à la position finale (Gainesville), de sorte que le vecteur de déplacement total peut être dessiné directement sous la forme d'une flèche reliant Tallahassee à Gainesville (voir le vecteur vert sur la figure\(\PageIndex{4}\)). Lorsque nous utilisons la règle du parallélogramme quatre fois, le résultat obtenu\(\vec{R}\) est exactement ce vecteur vert reliant Tallahassee à Gainesville :\(\vec{R}\) =\(\vec{A}\) + +\(\vec{B}\) +\(\vec{C}\) +\(\vec{D}\) +\(\vec{E}\).

Figure\(\PageIndex{4}\) : Lorsque nous utilisons quatre fois la règle du parallélogramme, nous obtenons le vecteur résultant\(\vec{R}\) =\(\vec{A}\) +\(\vec{B}\) +\(\vec{C}\) +\(\vec{D}\) +\(\vec{E}\), qui est le vecteur vert reliant Tallahassee à Gainesville.

Le dessin du vecteur résultant de nombreux vecteurs peut être généralisé en utilisant la construction géométrique de la queue à la tête suivante. Supposons que nous souhaitions dessiner le vecteur résultant\(\vec{R}\) de quatre vecteurs\(\vec{A}\)\(\vec{B}\),\(\vec{C}\), et\(\vec{D}\) (Figure\(\PageIndex{5a}\)). Nous sélectionnons l'un des vecteurs comme premier vecteur et effectuons une translation parallèle d'un second vecteur jusqu'à une position où l'origine (« queue ») du second vecteur coïncide avec la fin (« tête ») du premier vecteur. Ensuite, nous sélectionnons un troisième vecteur et effectuons une translation parallèle du troisième vecteur jusqu'à une position où l'origine du troisième vecteur coïncide avec la fin du deuxième vecteur. Nous répétons cette procédure jusqu'à ce que tous les vecteurs se trouvent dans un arrangement tête-à-queue comme celui illustré sur la figure\(\PageIndex{5}\). Nous dessinons le vecteur résultant\(\vec{R}\) en connectant l'origine (« queue ») du premier vecteur à la fin (« tête ») du dernier vecteur. La fin du vecteur résultant se trouve à la fin du dernier vecteur. Comme l'addition de vecteurs est associative et commutative, nous obtenons le même vecteur résultant quel que soit le vecteur que nous choisissons comme premier, deuxième, troisième ou quatrième dans cette construction.

Figure\(\PageIndex{5}\) : Méthode de la queue à tête pour dessiner le vecteur résultant\(\vec{R}\) =\(\vec{A}\) +\(\vec{B}\) +\(\vec{C}\) +\(\vec{D}\). a) Quatre vecteurs de grandeurs et de directions différentes. (b) Les vecteurs de (a) sont traduits vers de nouvelles positions où l'origine (« queue ») d'un vecteur se trouve à la fin (« tête ») d'un autre vecteur. Le vecteur résultant est tracé depuis l'origine (« queue ») du premier vecteur jusqu'à la fin (« tête ») du dernier vecteur dans cet arrangement.

Exemple\(\PageIndex{2}\): Geometric Construction of the Resultant

Les trois vecteurs de déplacement\(\vec{A}\)\(\vec{B}\), et\(\vec{C}\) dans la figure,\(\PageIndex{6}\) sont spécifiés par leurs magnitudes A = 10,0, B = 7,0 et C = 8,0, respectivement, et par leurs angles de direction respectifs avec la direction horizontale\(\alpha\) = 35°,\(\beta\) = −110° et\(\gamma\) = 30°. Les unités physiques des magnitudes sont les centimètres. Choisissez une échelle appropriée et utilisez une règle et un rapporteur pour trouver les sommes vectorielles suivantes : (a)\(\vec{R}\) =\(\vec{A}\) +\(\vec{B}\), (b)\(\vec{D}\) =\(\vec{A}\) −\(\vec{B}\) et (c)\(\vec{S}\) =\(\vec{A}\) −\(3 \vec{B}\) +\(\vec{C}\).

Figure\(\PageIndex{6}\) : Vecteurs utilisés dans l'exemple\(\PageIndex{2}\) et dans la fonction Exercice qui suit.

Stratégie

Dans la construction géométrique, trouver un vecteur signifie trouver sa magnitude et son angle de direction avec la direction horizontale. La stratégie consiste à dessiner pour redimensionner les vecteurs qui apparaissent sur le côté droit de l'équation et à construire le vecteur résultant. Ensuite, utilisez une règle et un rapporteur pour lire l'amplitude de la résultante et l'angle de direction. Pour les parties (a) et (b), nous utilisons la règle du parallélogramme. Pour (c), nous utilisons la méthode de la queue à la tête.

Solution

Pour les parties (a) et (b), nous attachons l'origine du vecteur\(\vec{B}\) à l'origine du vecteur\(\vec{A}\), comme indiqué sur la figure\(\PageIndex{7}\), et construisons un parallélogramme. La diagonale la plus courte de ce parallélogramme est la somme\(\vec{A}\) +\(\vec{B}\). La plus longue des diagonales est la différence\(\vec{A}\) -\(\vec{B}\). Nous utilisons une règle pour mesurer la longueur des diagonales et un rapporteur pour mesurer les angles avec l'horizontale. Pour la résultante\(\vec{R}\), on obtient R = 5,8 cm et\(\theta_{R}\) ≈ 0°. Pour la différence\(\vec{D}\), nous obtenons D = 16,2 cm et\(\theta_{D}\) = 49,3°, comme indiqué sur la figure\(\PageIndex{7}\).

Figure\(\PageIndex{7}\) : Utilisation de la règle du parallélogramme pour résoudre (a) (recherche de la résultante, rouge) et (b) (détermination de la différence, bleu).

Pour (c), nous pouvons commencer par le vecteur −3\(\vec{B}\) et dessiner les vecteurs restants tête à tête, comme indiqué sur la figure\(\PageIndex{8}\). En ce qui concerne l'ajout de vecteurs, l'ordre dans lequel nous dessinons les vecteurs n'a pas d'importance, mais il est très important de dessiner les vecteurs à l'échelle. Ensuite, nous dessinons un vecteur\(\vec{S}\) depuis l'origine du premier vecteur jusqu'à la fin du dernier vecteur et plaçons la pointe de flèche à la fin de\(\vec{S}\). Nous utilisons une règle pour mesurer la longueur de\(\vec{S}\) et constatons que sa magnitude est S = 36,9 cm. Nous utilisons un rapporteur et trouvons que son angle de direction est\(\theta_{S}\) = 52,9°. Cette solution est illustrée dans la figure\(\PageIndex{8}\).

Figure\(\PageIndex{8}\) : Utilisation de la méthode de la queue à tête pour résoudre (c) (vecteur de recherche\(\vec{S}\), vert).

Exercice 2.3

À l'aide des trois vecteurs de déplacement\(\vec{A}\)\(\vec{B}\), et\(\vec{F}\) dans la figure\(\PageIndex{6}\), choisissez une échelle appropriée et utilisez une règle et un rapporteur pour trouver le vecteur\(\vec{G}\) donné par l'équation vectorielle\(\vec{G}\) =\(\vec{A}\) +\(2 \vec{B}\) −\(\vec{F}\).

Simulation

Observez l'ajout de vecteurs dans un plan en consultant ce calculateur de vecteurs et cette simulation PhET.