Skip to main content
Global

15.6 : Résonance dans un circuit à courant alternatif

  1. Last updated
  2. Save as PDF
  • Page ID
    191201

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objectifs d'apprentissage

    À la fin de la section, vous serez en mesure de :

    • Déterminer la fréquence angulaire de résonance maximale en courant alternatif pour un circuit RLC
    • Expliquez la largeur de la courbe de puissance moyenne par rapport à la fréquence angulaire et sa signification en utilisant des termes tels que bande passante et facteur de qualité

    Dans le circuit de la série RLC de la Figure 15.4.1, l'amplitude du courant est, d'après l'équation 15.4.7,

    \[I_0 = \dfrac{V_0}{\sqrt{R^2 + (\omega L - 1/\omega C)^2}}. \label{15.15} \]

    Si nous pouvons faire varier la fréquence du générateur de courant alternatif tout en maintenant l'amplitude de sa tension de sortie constante, le courant change en conséquence. Un diagramme de\(I_0\) contre\(\omega\) est illustré sur la figure\(\PageIndex{1}\).

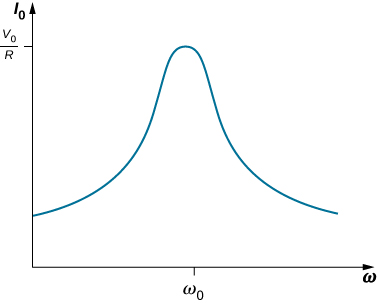
    La figure montre un graphique entre I0 et oméga. La courbe monte progressivement, présente un pic arrondi au centre, puis descend progressivement jusqu'à sa valeur initiale. La valeur y au pic est V0 par R et la valeur x est oméga 0.
    Figure\(\PageIndex{1}\) : À la fréquence de résonance d'un circuit RLC\(\omega_0 = \sqrt{1/LC}\), l'amplitude du courant est à sa valeur maximale.

    Dans Oscillations, nous avons rencontré un graphe similaire où l'amplitude d'un oscillateur harmonique amorti était tracée par rapport à la fréquence angulaire d'une force motrice sinusoïdale (voir Oscillations forcées). Cette similitude est bien plus qu'une simple coïncidence, comme l'a montré précédemment l'application de la règle de boucle de Kirchhoff au circuit de la Figure 15.4.1. Cela donne

    \[L\dfrac{di}{dt} + iR + \dfrac{q}{C} = V_0 \, \sin \, \omega t, \label{15.16}\]

    ou

    \[L\dfrac{d^2q}{dt^2} + R\dfrac{dq}{dt} + \dfrac{1}{C}q = V_0 \, \sin \, \omega t,\]

    où nous avons remplacé i (t) par dq (t)/dt. Une comparaison de l'équation \ ref {15.16} et, d'après Oscillations, des oscillations amorties pour le mouvement harmonique amorti montre clairement que le circuit de la série RLC piloté est l'analogue électrique de l'oscillateur harmonique amorti piloté.

    La fréquence\(f_0\) de résonance du circuit RLC est la fréquence à laquelle l'amplitude du courant est maximale et le circuit oscillerait s'il n'était pas alimenté par une source de tension. Par inspection, cela correspond à la fréquence angulaire\(\omega_0 = 2\pi f_0\) à laquelle l'impédance Z dans l'équation \ ref {15.15} est minimale, ou lorsque

    \[\omega_0 L = \dfrac{1}{\omega_0 C} \label{resonantfrequency1}\]

    et

    \[\omega_0 = \sqrt{\dfrac{1}{LC}}.\label{resonantfrequency2}\]

    Il s'agit de la fréquence angulaire de résonance du circuit. En les\(\omega_0\) substituant à l'équation 15.4.5, à l'équation 15.4.7 et à l'équation 15.4.8, nous trouvons qu'à la résonance,

    \[\phi = tan^{-1}(0) = 0, \, I_0 = V_0/R, \, and \, Z = R.\]

    Par conséquent, à la résonance, un circuit RLC est purement résistif, avec la force électromotrice et le courant appliqués en phase.

    Qu'advient-il de la puissance lors de la résonance ? L'équation 15.5.18 nous indique comment la puissance moyenne transférée d'un générateur de courant alternatif à la combinaison RLC varie en fonction de la fréquence. De plus,\(P_{ave}\) atteint un maximum lorsque\(Z\), qui dépend de la fréquence, est un minimum, c'est-à-dire quand\(X_L = X_C\) et\(Z = R\). Ainsi, à la résonance, la puissance de sortie moyenne de la source dans un circuit série RLC est maximale. À partir de l'équation 15.5.18, ce maximum est\(V_{rms}^2 /R\).

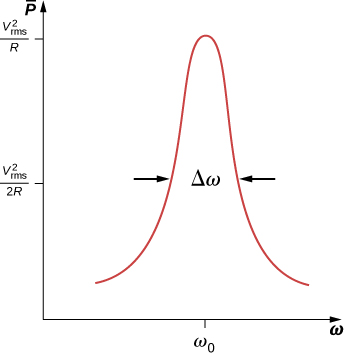
    La figure\(\PageIndex{2}\) est un diagramme typique de la\(P_{ave}\) comparaison avec\(\omega\) la région de la puissance de sortie maximale. La bande passante\(\Delta \omega\) du pic de résonance est définie comme la plage de fréquences angulaires\(\omega\) sur laquelle la puissance moyenne\(P_{ave}\) est supérieure à la moitié de la valeur maximale de\(P_{ave}\). La netteté du pic est décrite par une quantité sans dimension connue sous le nom de facteur de qualité Q du circuit. Par définition,

    \[Q = \dfrac{\omega_0}{\Delta \omega}, \label{15.18} \]

    où\(\omega_0\) est la fréquence angulaire de résonance. Un Q élevé indique un pic de résonance aigu. Nous pouvons donner Q en termes de paramètres du circuit comme

    \[Q = \dfrac{\omega_0L}{R}. \label{15.19} \]

    La figure montre un graphique de la barre P par rapport à l'oméga. La courbe monte progressivement, présente un pic arrondi au centre, puis descend progressivement jusqu'à sa valeur initiale. La valeur y au pic est l'indice V carré rms par R et la valeur x est oméga 0. La valeur y située près du milieu de la courbe est V, indice carré rms par 2R. La largeur de la courbe près du milieu est désignée delta oméga.
    Figure\(\PageIndex{2}\) : Comme le courant, la puissance moyenne transférée d'un générateur de courant alternatif à un circuit RLC culmine à la fréquence de résonance.

    Les circuits résonnants sont couramment utilisés pour laisser passer ou rejeter des plages de fréquences sélectionnées. Cela se fait en ajustant la valeur de l'un des éléments et en « réglant » ainsi le circuit sur une fréquence de résonance particulière. Par exemple, dans les radios, le récepteur est accordé à la station souhaitée en ajustant la fréquence de résonance de ses circuits pour qu'elle corresponde à la fréquence de la station. Si le circuit de réglage a un Q élevé, il aura une faible bande passante, de sorte que les signaux provenant d'autres stations à des fréquences même légèrement différentes de la fréquence de résonance rencontrent une impédance élevée et ne sont pas transmis par le circuit. Les téléphones portables fonctionnent de la même manière, communiquant avec des signaux d'environ 1 GHz qui sont réglés par un circuit inducteur-condensateur. L'une des applications les plus courantes des condensateurs est leur utilisation dans des circuits de temporisation à courant alternatif, basés sur l'obtention d'une fréquence de résonance. Un détecteur de métaux utilise également un changement de fréquence de résonance pour détecter les métaux (Figure\(\PageIndex{3}\)).

    Photographie d'un plongeur sous-marin utilisant un détecteur de métaux.
    Figure\(\PageIndex{3}\) : Lorsqu'un détecteur de métaux s'approche d'une pièce de métal, l'inductance propre de l'une de ses bobines change. Cela provoque un décalage de la fréquence de résonance d'un circuit contenant la bobine. Ce décalage est détecté par les circuits et transmis au plongeur au moyen des écouteurs.
    Exemple\(\PageIndex{1}\): Resonance in an RLC Series Circuit
    1. Quelle est la fréquence de résonance du circuit de l'exemple 15.3.1 ?
    2. Si le générateur de courant alternatif est réglé sur cette fréquence sans modifier l'amplitude de la tension de sortie, quelle est l'amplitude du courant ?

    Stratégie

    La fréquence de résonance d'un circuit RLC est calculée à partir de l'équation \ ref {resonantfrequency2}, qui provient d'un équilibre entre les réactances du condensateur et de l'inducteur. Comme le circuit est en résonance, l'impédance est égale à la résistance. Ensuite, le courant de pointe est calculé par la tension divisée par la résistance.

    Solution

    1. La fréquence de résonance est trouvée à partir de l'équation \ ref {resonantfrequency2} :\[\begin{align*} f_0 &= \dfrac{1}{2\pi} \sqrt{\dfrac{1}{LC}} \\[4pt] &= \dfrac{1}{2\pi}\sqrt{\dfrac{1}{(3.00 \times 10^{-3} H)(8.00 \times 10^{-4}F)}} \\[4pt] &= 1.03 \times 10^2 \, Hz. \end{align*}\]
    2. À la résonance, l'impédance du circuit est purement résistive et l'amplitude du courant est\[I_0 = \dfrac{0.100 \, V}{4.00 \, \Omega} = 2.50 \times 10^{-2}A. \nonumber\]

    L'importance

    Si le circuit n'était pas réglé sur la fréquence de résonance, nous aurions besoin de l'impédance de l'ensemble du circuit pour calculer le courant.

    Exemple\(\PageIndex{2}\): Power Transfer in an RLC Series Circuit at Resonance
    1. Quelle est la fréquence angulaire de résonance d'un circuit RLC avec\( R = 0.200 \, \Omega, \, L = 4.00 \times 10^{-3} H\) et\(C = 2.00 \times 10^{-6}F\) ?
    2. Si une source de courant alternatif d'amplitude constante de 4,00 V est réglée sur cette fréquence, quelle est la puissance moyenne transférée au circuit ?
    3. Déterminez Q et la bande passante de ce circuit.

    Stratégie

    La fréquence angulaire de résonance est calculée à partir de l'équation \ ref {resonantfrequency2}. La puissance moyenne est calculée à partir de la tension efficace et de la résistance du circuit. Le facteur de qualité est calculé à partir de l'équation \ ref {15.19} et en connaissant la fréquence de résonance. La bande passante est calculée à partir de l'équation \ ref {15.18} et en connaissant le facteur de qualité.

    Solution

    1. La fréquence angulaire de résonance est\[ \begin{align*} \omega_0 &= \sqrt{\dfrac{1}{LC}} \\[4pt] &= \sqrt{\dfrac{1}{(4.00 \times 10^{-3}H)(2.00 \times 10^{-6}F)}} \\[4pt] &= 1.12 \times 10^4 \, rad/s. \end{align*}\]
    2. À cette fréquence, la puissance moyenne transférée au circuit est maximale. C'est\[P_{ave} = \dfrac{V_{rms}^2}{R} = \dfrac{[(1/\sqrt{2})(4.00 \, V)]^2}{0.200 \, \Omega} = 40.0 \, W.\]
    3. Le facteur de qualité du circuit est\[Q = \dfrac{\omega_0L}{R} = \dfrac{(1.12 \times 10^4 \, rad/s)(4.00 \times 10^{-3}H)}{0.200 \, \Omega} = 224. \nonumber\] On trouve alors pour la bande passante\[\Delta \omega = \dfrac{\omega_0}{Q} = \dfrac{1.12 \times 10^4 \, rad/s}{224} = 50.0 \, rad/s. \nonumber\]

    L'importance

    Si une bande passante plus étroite est souhaitée, une résistance plus faible ou une inductance plus élevée peuvent aider. Cependant, une résistance plus faible augmente la puissance transférée au circuit, ce qui peut ne pas être souhaitable, en fonction de la puissance maximale qui pourrait éventuellement être transférée.

    Exercice\(\PageIndex{1}\)

    Dans le circuit de la Figure 15.4.1\(L = 2.0 \times 10^{-3}H, \, C = 5.0 \times 10^{-4} F\), et\(R = 40 \, \Omega\).

    1. Qu'est-ce que la fréquence de résonance ?
    2. Quelle est l'impédance du circuit à la résonance ?
    3. Si l'amplitude de la tension est de 10 V, qu'est-ce que i (t) à la résonance ?
    4. La fréquence du générateur de courant alternatif est maintenant passée à 200 Hz. Calculez la différence de phase entre le courant et la force électromotrice du générateur.
    Réponse

    environ 160 Hz ; b.\(40 \Omega\) ; c.\((0.25 A) \, \sin \, 10^3t\) ; d. 0,023 rad

    Exercice\(\PageIndex{2}\)

    Qu'arrive-t-il à la fréquence de résonance d'un circuit série RLC lorsque les quantités suivantes sont augmentées d'un facteur 4 : (a) la capacité, (b) l'auto-inductance et (c) la résistance ?

    Réponse

    a. coupé en deux ; b. coupé en deux ; c. identique

    Exercice\(\PageIndex{3}\)

    La fréquence angulaire de résonance d'un circuit de la série RLC est\(4.0 \times 10^2 \, rad/s\). Une source de courant alternatif fonctionnant à cette fréquence transfère une puissance moyenne de\(2.0 \times 10^{-2} W\) au circuit. La résistance du circuit est\(0.50 \, \Omega\). Ecrivez une expression pour la force électromotrice de la source.

    Réponse

    \(v(t) = (0.14 \, V) \, sin \, (4.0 \times 10^2 t)\)