14.5 : Circuits RL
- Page ID
- 191147
À la fin de cette section, vous serez en mesure de :
- Analysez les circuits dotés d'une inductance et d'une résistance en série
- Décrire comment le courant et la tension augmentent ou diminuent de façon exponentielle en fonction des conditions initiales
Un circuit à résistance et à auto-inductance est connu sous le nom de circuit RL. La figure\(\PageIndex{1a}\) montre un circuit RL composé d'une résistance, d'une inductance, d'une source constante de champs électromagnétiques et de commutateurs\(S_1\) et\(S_2\). Lorsqu'il\(S_1\) est fermé, le circuit est équivalent à un circuit à boucle unique composé d'une résistance et d'une inductance connectées à une source de force électromotrice (Figure\(\PageIndex{1b}\)). Lorsqu'il\(S_1\) est ouvert et\(S_2\) fermé, le circuit devient un circuit à boucle unique avec uniquement une résistance et une inductance (Figure\(\PageIndex{1c}\)).
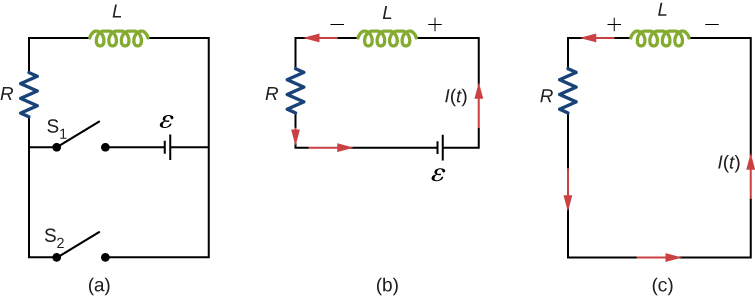
Nous considérons d'abord le circuit RL de la Figure\(\PageIndex{1b}\). Une fois\(S_1\) fermée et\(S_2\) ouverte, la source de force électromotrice produit un courant dans le circuit. S'il n'y avait pas d'auto-inductance dans le circuit, le courant augmenterait immédiatement pour atteindre une valeur constante de\(\epsilon/R\). Cependant, selon la loi de Faraday, le courant croissant produit une force électromotrice\(V_L = -L(dI/dt)\) à travers l'inducteur. Conformément à la loi de Lenz, la force électromotrice induite neutralise l'augmentation du courant et est dirigée comme indiqué sur la figure. Par conséquent,\(I(t)\) commence à zéro et augmente de façon asymptotique jusqu'à sa valeur finale.
En appliquant la règle de boucle de Kirchhoff à ce circuit, nous obtenons
\[\epsilon - L\dfrac{dI}{dt} - IR = 0, \label{eq1}\]
qui est une équation différentielle du premier ordre pour\(I(t)\). Remarquez sa similitude avec l'équation d'un condensateur et d'une résistance en série (voir Circuits RC). De même, la solution de l'équation \ ref {eq1} peut être trouvée en effectuant des substitutions dans les équations reliant le condensateur à l'inducteur. Cela donne
\[ \begin{align} I(t) &= \dfrac{\epsilon}{R}(1 - e^{-Rt/L}) \\[4pt] &= \dfrac{\epsilon}{R}(1 - e^{-t/\tau_L}),\label{eq3} \end{align}\]
où
\[\tau_L = L/R \label{eq5}\]
est la constante de temps inductive du circuit.
Le courant\(I(t)\) est représenté sur la figure\(\PageIndex{2a}\). Il commence à zéro et se\(I(t)\) rapproche\(t \rightarrow \infty\) de manière\(\epsilon/R\) asymptotique. La force\(V_L(t)\) électromotrice induite est directement proportionnelle à\(dI/dt\) la pente de la courbe. Ainsi, alors qu'elle atteint son maximum immédiatement après le déclenchement des commutateurs, la force électromotrice induite diminue à zéro avec le temps à mesure que le courant approche de sa valeur finale de\(\epsilon/R\). Le circuit devient alors équivalent à une résistance connectée à une source de force électromotrice.
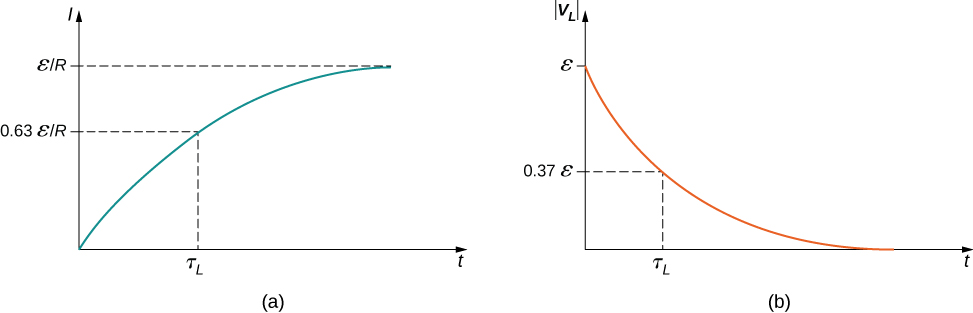
L'énergie stockée dans le champ magnétique d'un inducteur est
\[U_L = \dfrac{1}{2}LI^2.\]
Ainsi, lorsque le courant approche du courant maximum\(\epsilon/R\), l'énergie stockée dans l'inducteur augmente à partir de zéro et se rapproche asymptotiquement d'un maximum de\(L(\epsilon/R)^2 /2\).
La constante de temps nous\(\tau_L\) indique à quelle vitesse le courant augmente jusqu'à sa valeur finale. At\(t = \tau_L\), le courant dans le circuit est, d'après l'équation \ ref {eq3},
\[I(\tau_L) = \dfrac{\epsilon}{R}(1 - e^{-1}) = 0.63 \dfrac{\epsilon}{R},\]
qui est\(63\%\) de la finale\(\epsilon/R\). Plus la constante de temps inductive est faible\(\tau_L = L/R\), plus le courant approche rapidement\(\epsilon/R\).
Nous pouvons déterminer la dépendance temporelle de la tension induite aux bornes de l'inducteur de ce circuit en utilisant\(V_L(t) = -L(dI/dt)\) l'équation \ ref {eq3} :
\[V_L(t) = -L\dfrac{dI}{dt} = -\epsilon e^{-t/\tau_L}.\]
L'amplitude de cette fonction est représentée sur la figure\(\PageIndex{2b}\). La plus grande valeur de\(L(dI/dt)\) est\(\epsilon\) ; elle se produit lorsque\(dI/dt\) est la plus grande, c'est-à-dire immédiatement après\(S_1\) la fermeture et\(S_2\) l'ouverture. À l'approche de l'état d'équilibre,\(dI/dt\) diminue à zéro. Par conséquent, la tension aux bornes de l'inducteur disparaît également au fur et à mesure\(t \rightarrow \infty\).
La constante de temps nous indique\(\tau_L\) également à quelle vitesse la tension induite diminue. À\(t = \tau_L\) l'amplitude de la tension induite est
\[|V_L(\tau_L)| = \epsilon e^{-1} = 0.37 \epsilon = 0.37 V(0).\]
La tension aux bornes de l'inducteur chute donc à peu près\(37\%\) à sa valeur initiale après une constante de temps. Plus la constante de temps est courte\(\tau_L\), plus la tension diminue rapidement.
Une fois que suffisamment de temps s'est écoulé pour que le courant atteigne essentiellement sa valeur finale, les positions des interrupteurs de la figure\(\PageIndex{1a}\) sont inversées, nous donnant le circuit de la partie (c). À\(t = 0\), le courant dans le circuit est de\(I(0) = \epsilon/R\). Avec la règle de boucle de Kirchhoff, nous obtenons
\[IR + L\dfrac{dI}{dt} = 0.\]
La solution de cette équation est similaire à la solution de l'équation pour un condensateur de décharge, avec des substitutions similaires. Le courant à l'instant t est alors
\[I(t) = \dfrac{\epsilon}{R}e^{-t/\tau_L}.\]
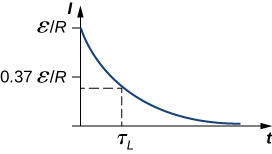
Le courant commence à\(I(0) = \epsilon/R\) et diminue avec le temps à mesure que l'énergie stockée dans l'inducteur s'épuise (Figure\(\PageIndex{3}\)).
La dépendance temporelle de la tension aux bornes de l'inducteur peut être déterminée à partir de\(V_L = -L(dI/dt)\) :
\[V_L(0) = \epsilon e^{-t/\tau_L}. \label{14.32}\]
Cette tension est initiale\(V_L(0) = \epsilon\), et elle décroît à zéro comme le courant. L'énergie stockée dans le champ magnétique de l'inducteur diminue également de façon exponentielle avec le temps, car elle est dissipée par le chauffage par joule dans la résistance du circuit.\(LI^2/2\)
Dans le circuit de Figure\(\PageIndex{1a}\)\(\epsilon = 2.0 \, V, \, R = 4.0 \, \Omega\), laissez et\(L = 4.0 \, H\). Avec\(S_1\) fermé et\(S_2\) ouvert (Figure\(\PageIndex{1b}\)), (a) quelle est la constante de temps du circuit ? (b) Quels sont le courant dans le circuit et l'amplitude de la force électromotrice induite à travers l'inducteur\(t = 0,\) à at\(t = 2.0 \tau_L\) et as\(t \rightarrow \infty\) ?
Stratégie
La constante de temps pour une inductance et une résistance dans un circuit en série est calculée à l'aide de l'équation \ ref {eq5}. Le courant traversant et la tension aux bornes de l'inducteur sont calculés selon les scénarios détaillés à partir de l'équation \ ref {eq3} et de l'équation \ ref {14.32}.
Solution
- La constante de temps inductive est\[\tau_L = \dfrac{L}{R} = \dfrac{4.0 \, H}{4.0 \, \Omega} = 1.0 \, s.\]
- Le courant dans le circuit de la Figure\(\PageIndex{1b}\) augmente selon l'équation \ ref {eq3} :\[I(t) = \dfrac{\epsilon}{R}(1 - e^{-t/\tau_L}). \nonumber\] At\(t = 0\), At\(t = 2.0 \tau_L\) et\(t \rightarrow \infty\), respectivement,\[I(2.0\tau_L) = \dfrac{\epsilon}{R}(1 - e^{-2.0}) = (0.50 \, A)(0.86) = 0.43 \, A \nonumber\] et\[(1 - e^{-t/\tau_L}) = (1 - 1) = 0; \, so \, I(0) = 0. \nonumber\] à\[I(\infty) = \dfrac{\epsilon}{R} = 0.50 \, A. \nonumber\] partir de l'équation \ ref {14.32}, l'amplitude de la force électromotrice induite décroît en tant que\[|V_L(t)| = \epsilon e^{-t/\tau_L}. \nonumber\] At\(t = 0\), \(t = 2.0 \tau_L\), et au fur\(t \rightarrow \infty\) et à mesure que nous obtenons\[|V_L(0)| = \epsilon = \, V,\]\[|V_L(2.0 \tau_L)| = (2.0 \, V) e^{-2.0} = 0.27 \, V\]\[|V_L(\infty)| = 0.\nonumber\]
L'importance
Si le temps de la mesure était beaucoup plus long que la constante de temps, nous ne verrions pas de baisse ou de croissance de la tension aux bornes de l'inducteur ou de la résistance. Le circuit atteindrait rapidement les valeurs asymptotiques pour les deux (Figure\(\PageIndex{4}\)).
Une fois que le courant dans le circuit RL de l'exemple\(\PageIndex{1}\) a atteint sa valeur finale, les positions des commutateurs sont inversées de sorte que le circuit devienne celui illustré sur la figure\(\PageIndex{1c}\).
- Combien de temps faut-il au courant pour atteindre la moitié de sa valeur initiale ?
- Combien de temps faut-il pour que l'énergie stockée dans l'inducteur soit réduite à\(1.0 \%\) sa valeur maximale ?
Stratégie
Le courant dans l'inducteur va maintenant diminuer à mesure que la résistance dissipe cette énergie. Par conséquent, le courant diminue sous forme de décroissance exponentielle. Nous pouvons également utiliser cette même relation pour remplacer l'énergie contenue dans une formule d'inductance afin de déterminer comment l'énergie diminue à différents intervalles de temps.
Solution
- Lorsque les commutateurs sont inversés, le courant diminue selon A un\[I(t) = \dfrac{\epsilon}{R}e^{-t/\tau_L} = I(0)e^{-t/\tau_L}.\nonumber\] instant t où le courant est égal à la moitié de sa valeur initiale, nous avons\[I(t) = 0.50 I(0)\space so \, e^{-t/\tau_L} = 0.50,\nonumber\] et\[t = -[\ln(0.50)]\tau_L = 0.69 (1.0 \, s) = 0.69 \, s\nonumber\] où nous avons utilisé la constante de temps inductive trouvée dans l'exemple\(\PageIndex{1}\).
- L'énergie stockée dans l'inducteur est donnée par\[U_L(t) = \dfrac{1}{2}L[I(t)]^2 = \dfrac{1}{2}L\left(\dfrac{\epsilon}{R} e^{-t/\tau_L}\right)^2 = \dfrac{L\epsilon^2}{2R^2}e^{-2t/\tau_L}.\nonumber\] Si l'énergie tombe à\(1.0\%\) sa valeur initiale à un moment t, nous avons\[U_L(t) = (0.010)U_L(0) \, or \, \dfrac{L\epsilon^2}{2R^2} e^{-2t/\tau_L} = (0.010)\dfrac{L\epsilon^2}{2R^2}.\nonumber\] En annulant les termes et en prenant le logarithme naturel des deux côtés, nous l'obtenons\[-\dfrac{2t}{\tau_L} = \ln(0.010),\] ainsi.\[t = -\dfrac{1}{2} \tau_L \ln(0.010).\nonumber\] Puisque\(\tau_L = 1.0 \, s\), le temps qu'il faut pour l'énergie stockée dans l'inducteur pour diminuer jusqu'à\(1.0\%\) sa valeur initiale est\[t = -\dfrac{1}{2}(1.0 \, s)\ln(0.010) = 2.3 \, s.\nonumber\]
L'importance
Ce calcul ne fonctionne que si le circuit est au courant maximal dans la situation (b) antérieure à cette nouvelle situation. Sinon, nous commençons avec un courant initial plus faible, qui diminuera selon la même relation.
Vérifiez que RC et L/R ont les dimensions du temps
- Si le courant dans le circuit de la figure\(\PageIndex{1b}\) augmente jusqu'à\(90\%\) sa valeur finale après 5,0 s, quelle est la constante de temps inductive ?
- Si\(R = 20 \, \Omega\), quelle est la valeur de l'auto-inductance ?
- Si la\(R = 20 \, \Omega\) résistance est remplacée par une\(R = 100 \, \Omega\) résistance, quel est le temps nécessaire pour que le courant atteigne\(90\%\) sa valeur finale ?
- Réponse
-
a. 2,2 s ; b. 43 H ; environ 1,0 s
Pour le circuit de la figure\(\PageIndex{1b}\) 2, montrez que lorsque l'état stable est atteint, la différence entre les énergies totales produites par la batterie et dissipées dans la résistance est égale à l'énergie stockée dans le champ magnétique de la bobine


