14.6 : Oscillations dans un circuit LC
- Page ID
- 191157
À la fin de cette section, vous serez en mesure de :
- Expliquer pourquoi la charge ou le courant oscille entre un condensateur et une bobine d'induction, respectivement, lorsqu'ils sont connectés en série
- Décrire la relation entre la charge et le courant oscillant entre un condensateur et une bobine d'induction câblés en série
Il convient de noter que les condensateurs et les inducteurs stockent de l'énergie, respectivement dans leurs champs électriques et magnétiques. Un circuit contenant à la fois un inducteur (L) et un condensateur (C) peut osciller sans source de force électromotrice en déplaçant l'énergie stockée dans le circuit entre les champs électrique et magnétique. Ainsi, les concepts que nous développons dans cette section sont directement applicables à l'échange d'énergie entre les champs électriques et magnétiques des ondes électromagnétiques, ou de la lumière. Nous commençons par un circuit idéalisé de résistance nulle qui contient une inductance et un condensateur, un circuit LC.
Un circuit LC est illustré sur la figure\(\PageIndex{1}\). Si le condensateur contient une charge\(q_0\) avant la fermeture de l'interrupteur, toute l'énergie du circuit est initialement stockée dans le champ électrique du condensateur (Figure\(\PageIndex{1a}\)). Cette énergie est
\[U_C = \frac{1}{2} \frac{q_0^2}{C}.\]
Lorsque l'interrupteur est fermé, le condensateur commence à se décharger, produisant un courant dans le circuit. Le courant crée à son tour un champ magnétique dans l'inducteur. L'effet net de ce processus est un transfert d'énergie du condensateur, avec son champ électrique décroissant, vers l'inducteur, dont le champ magnétique augmente.
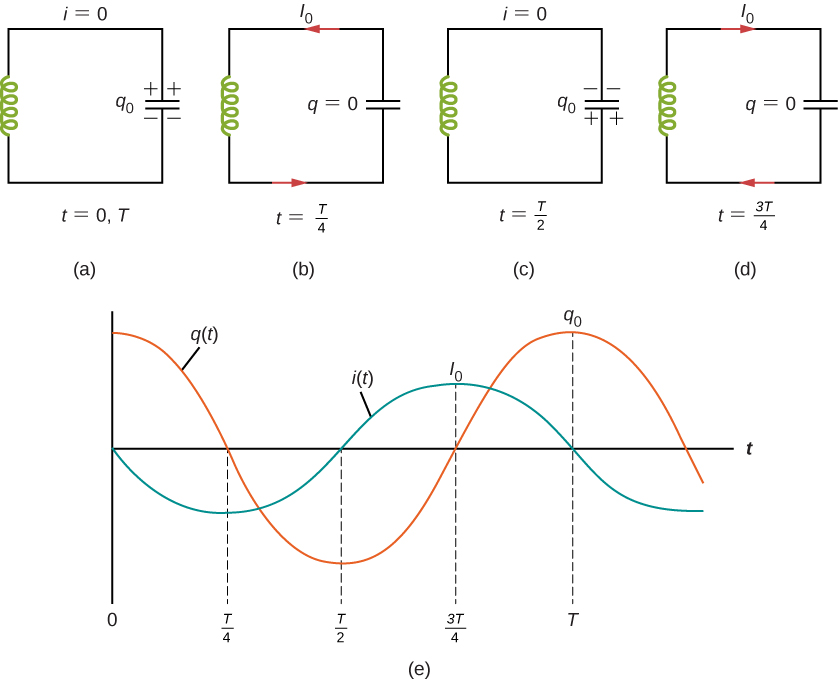
Sur la figure\(\PageIndex{1b}\), le condensateur est complètement déchargé et toute l'énergie est stockée dans le champ magnétique de l'inducteur. À ce moment, le courant est à sa valeur maximale\(I_0\) et l'énergie dans l'inducteur est
\[U_L = \frac{1}{2} LI_0^2.\]
Comme il n'y a pas de résistance dans le circuit, aucune énergie n'est perdue par le chauffage par joule ; ainsi, l'énergie maximale stockée dans le condensateur est égale à l'énergie maximale stockée ultérieurement dans l'inducteur :
\[\frac{1}{2} \frac{q_0^2}{C} = \frac{1}{2} LI_0^2.\]
À un moment arbitraire où la charge du condensateur est q (t) et le courant est i (t), l'énergie totale U dans le circuit est donnée par
\[\frac{q^2(t)}{2C} + \frac{Li^2}{2}.\]
Comme il n'y a pas de dissipation d'énergie,
\[U = \frac{1}{2} \frac{q^2}{C} + \frac{1}{2}Li^2 = \frac{1}{2} \frac{q_0^2}{C} = \frac{1}{2}LI_0^2.\]
Après avoir atteint son maximum\(I_0\), le courant i (t) continue de transporter la charge entre les plaques du condensateur, rechargeant ainsi le condensateur. Comme l'inducteur résiste à un changement de courant, le courant continue de circuler, même si le condensateur est déchargé. Ce courant continu amène le condensateur à se charger avec une polarité opposée. Le champ électrique du condensateur augmente tandis que le champ magnétique de l'inducteur diminue, et l'effet global est un transfert d'énergie de l'inducteur vers le condensateur. Selon la loi de conservation de l'énergie, la charge maximale que le condensateur acquiert à nouveau est\(q_0\). Cependant, comme le\(\PageIndex{1c}\) montre la figure, les plaques de condensateur sont chargées à l'opposé de ce qu'elles étaient initialement.
Une fois complètement chargé, le condensateur transfère à nouveau son énergie à l'inducteur jusqu'à ce qu'il soit à nouveau complètement déchargé, comme indiqué sur la figure\(\PageIndex{1d}\). Ensuite, dans la dernière partie de ce processus cyclique, l'énergie retourne au condensateur et l'état initial du circuit est rétabli.
Nous avons suivi le circuit tout au long d'un cycle complet. Ses oscillations électromagnétiques sont analogues aux oscillations mécaniques d'une masse à l'extrémité d'un ressort. Dans ce dernier cas, l'énergie est transférée d'avant en arrière entre la masse, qui possède de l'énergie cinétique\(mv^2/2\), et le ressort, qui possède de l'énergie potentielle\(kx^2/2\). En l'absence de friction dans le système masse-ressort, les oscillations se poursuivraient indéfiniment. De même, les oscillations d'un circuit LC sans résistance se poursuivraient éternellement si elles n'étaient pas perturbées ; cependant, ce circuit LC idéal à résistance nulle n'est pas pratique, et tout circuit LC aura au moins une faible résistance, qui rayonnera et perdra de l'énergie avec le temps.
La fréquence des oscillations dans un circuit LC sans résistance peut être déterminée par analogie avec le système masse-ressort. Pour le circuit\(i(t) = dq(t)/dt\), l'énergie électromagnétique totale U est
\[U = \frac{1}{2}Li^2 + \frac{1}{2} \frac{q^2}{C}.\]
Pour le système masse-ressort\(v(t) = dx(t)/dt\), l'énergie mécanique totale E est
\[E = \frac{1}{2}mv^2 + \frac{1}{2}kx^2.\]
L'équivalence des deux systèmes est claire. Pour passer du système mécanique au système électromagnétique, il suffit de remplacer m par L, v par i, k par 1/ C et x par q. Maintenant x (t) est donné par
\[x(t) = A \, cos (\omega t + \phi)\]où\(\omega = \sqrt{k/m}\). Par conséquent, la charge du condensateur dans un circuit LC est donnée par
\[q(t) = q_0 \, cos (\omega t + \phi) \label{14.40}\]
où la fréquence angulaire des oscillations dans le circuit est
\[\omega = \sqrt{\frac{1}{LC}}. \label{14.41}\]
Enfin, le courant dans le circuit LC est déterminé en prenant la dérivée temporelle de q (t) :
\[i(t) = \frac{dq(t)}{dt} = - \omega q_0 \, sin(\omega t + \phi).\]
Les variations temporelles de q et I sont illustrées dans la figure\(\PageIndex{1e}\) for\(\phi = 0\).
Dans un circuit LC, l'inductance propre est\(2.0 \times 10^{-2}\) H et la capacité est\(8.0 \times 10^{-6}\) F.\(t = 0\) Toute l'énergie est stockée dans le condensateur, qui a la charge\(1.2 \times 10^{-5}\) C. (a) Quelle est la fréquence angulaire des oscillations dans le circuit ? (b) Quel est le courant maximal qui traverse le circuit ? (c) Combien de temps faut-il au condensateur pour se décharger complètement ? (d) Trouvez une équation qui représente q (t).
Stratégie
La fréquence angulaire du circuit LC est donnée par l'équation \ ref {14.41}. Pour trouver le courant maximum, l'énergie maximale dans le condensateur est définie comme égale à l'énergie maximale dans l'inducteur. Le temps nécessaire pour que le condensateur se décharge s'il est initialement chargé est le quart de la période du cycle, donc si nous calculons la période de l'oscillation, nous pouvons savoir ce que représente un quart de cette période. Enfin, connaissant la charge initiale et la fréquence angulaire, nous pouvons établir une équation en cosinus pour trouver q (t).
Solution
- À partir de l'équation \ ref {14.41}, la fréquence angulaire des oscillations est\[\omega = \sqrt{\frac{1}{LC}} = \sqrt{\frac{1}{(2.0 \times 10^{-2} \, H)(8.0 \times 10^{-6} \, F)}} = 2.5 \times 10^3 \, rad/s.\]
- Le courant est maximal\(I_0\) lorsque toute l'énergie est stockée dans l'inducteur. À partir de la loi de conservation de l'énergie,\[\frac{1}{2}LI_0^2 = \frac{1}{2} \frac{q_0^2}{C},\]\[I_0 = \sqrt{\frac{1}{LC}}q_0 = (2.5 \times 10^3 \, rad/s)(1.2 \times 10^{-5} C) = 3.0 \times 10^{-2} A.\] ce résultat peut également être trouvé par analogie avec un mouvement harmonique simple, où le courant et la charge sont la vitesse et la position d'un oscillateur.
- Le condensateur se décharge complètement en un quart de cycle, ou pendant un temps T /4, où T est la période des oscillations. Étant donné que\[T = \frac{2\pi}{\omega} = \frac{2\pi}{2.5 \times 10^3 \, rad/s} = 2.5 \times 10^{-3} s,\] le temps nécessaire pour que le condensateur se décharge complètement est de\((2.5 \times 10^{-3} s)/4 = 6.3 \times 10^{-4}s\).
- Le condensateur est complètement chargé à\(t = 0\), donc\(q(0) = q_0\). En utilisant \ ref {14.40}, nous obtenons\[q(0) = q_0 = q_0 \, cos \, \phi.\] Thus\(\phi = 0\), et\[q(t) = (1.2 \times 10^{-5} C) cos (2.5 \times 10^3 t).\]
L'importance
La relation énergétique établie dans la partie (b) n'est pas le seul moyen d'assimiler les énergies. La plupart du temps, une partie de l'énergie est stockée dans le condensateur et une partie de l'énergie est stockée dans l'inducteur. Nous pouvons placer les deux termes de chaque côté de l'équation. En examinant le circuit uniquement lorsqu'il n'y a aucune charge sur le condensateur ou aucun courant dans l'inducteur, nous simplifions l'équation énergétique.
La fréquence angulaire des oscillations dans un circuit LC est\(2.0 \times 10^3 \) rad/s. (a) Si\(L = 0.10 \, H\), qu'est-ce que C ? (b) Supposons que l'\(t = 0\)énergie soit stockée dans l'inducteur. Quelle est la valeur de\(\phi\) ? (c) Un second condensateur identique est connecté en parallèle au condensateur d'origine. Quelle est la fréquence angulaire de ce circuit ?
Solution
a.\(2.5 \, \mu F\) ; b.\(\pi /2 \) rad ou\(3\pi /2\) rad ; c.\(1.4 \times 10^3\) rad/s


