14.4 : Énergie dans un champ magnétique

Last updated
Save as PDF

Page ID: 191146

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objectifs d'apprentissage

À la fin de cette section, vous serez en mesure de :

Expliquer comment l'énergie peut être stockée dans un champ magnétique
Dérivez l'équation de l'énergie stockée dans un câble coaxial en fonction de la densité d'énergie magnétique

L'énergie d'un condensateur est stockée dans le champ électrique entre ses plaques. De même, un inducteur a la capacité de stocker de l'énergie, mais dans son champ magnétique. Cette énergie peut être trouvée en intégrant la densité d'énergie magnétique,

\[u_m = \dfrac{B^2}{2\mu_0}\]

au-dessus du volume approprié. Pour comprendre d'où vient cette formule, examinons le long solénoïde cylindrique de la section précédente. Encore une fois, en utilisant l'approximation infinie du solénoïde, nous pouvons supposer que le champ magnétique est essentiellement constant et donné par\(B = \mu_0 nI\) tout ce qui se trouve à l'intérieur du solénoïde. Ainsi, l'énergie stockée dans un solénoïde ou la densité d'énergie magnétique multipliée par le volume est équivalente à

\[U = u_m(V) = \dfrac{(\mu_0nI)^2}{2\mu_0}(Al) = \dfrac{1}{2}(\mu_0n^2Al)I^2. \label{14.19}\]

Avec la substitution de l'équation 14.3.12, cela devient

\[\boxed{U = \dfrac{1}{2}LI^2.}\]

Bien que dérivée pour un cas particulier, cette équation donne l'énergie stockée dans le champ magnétique de n'importe quel inducteur. Nous pouvons le constater en considérant un inducteur arbitraire à travers lequel passe un courant variable. À tout instant, l'amplitude de la force électromotrice induite est de\(\epsilon = Ldi/dt\), où i est le courant induit à cet instant. Par conséquent, la puissance absorbée par l'inducteur est

\[P = \epsilon i = L\dfrac{di}{dt}i.\]

L'énergie totale stockée dans le champ magnétique lorsque le courant augmente de 0 à I dans un intervalle de temps allant de 0 à t peut être déterminée en intégrant cette expression :

\[U = \int_0^t Pdt' = \int_0^t L\dfrac{di}{dt'}idt' = L\int_0^l idi = \dfrac{1}{2}LI^2. \label{14.22}\]

Exemple\(\PageIndex{1}\): Self-Inductance of a Coaxial Cable

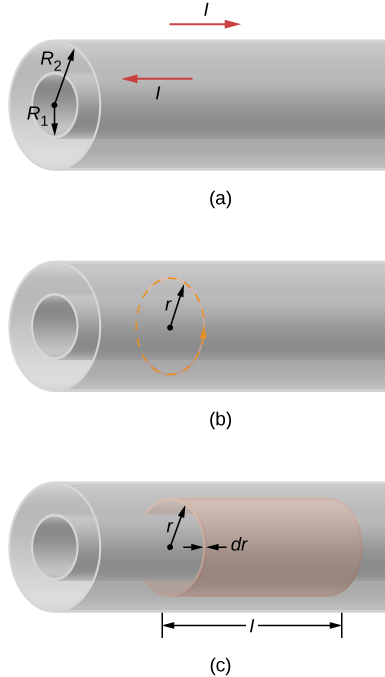
La figure\(\PageIndex{1}\) montre deux longues coques cylindriques concentriques de rayons\(R_1\) et\(R_2\). Comme indiqué dans Capacité sur capacité, cette configuration est une représentation simplifiée d'un câble coaxial. La capacité par unité de longueur du câble a déjà été calculée. Maintenant (a) déterminez l'énergie magnétique stockée par unité de longueur du câble coaxial et (b) utilisez ce résultat pour déterminer l'auto-inductance par unité de longueur du câble.

La figure a montre deux cylindres creux disposés de manière concentrique. Le rayon de l'intérieur est R1 et celui de l'extérieur est R2. La figure 2 montre un cercle en pointillés avec un rayon r entre les deux cylindres. La figure c montre un cylindre de longueur et de rayon r entre les deux cylindres. Son épaisseur est sèche. — Figure\(\PageIndex{1}\) : (a) Un câble coaxial est représenté ici par deux conducteurs cylindriques concentriques creux le long desquels le courant électrique circule dans des directions opposées. (b) Le champ magnétique entre les conducteurs peut être déterminé en appliquant la loi d'Ampère au chemin pointillé. (c) La coque cylindrique est utilisée pour trouver l'énergie magnétique stockée sur une longueur l du câble.

Stratégie

Le champ magnétique à l'intérieur et à l'extérieur du câble coaxial est déterminé par la loi d'Ampère. Sur la base de ce champ magnétique, nous pouvons utiliser l'équation \ ref {14.22} pour calculer la densité d'énergie du champ magnétique. L'énergie magnétique est calculée par une intégrale de la densité d'énergie magnétique multipliée par le volume différentiel au-dessus de la coque cylindrique. Une fois l'intégration terminée, nous disposons d'une solution sous forme fermée pour la partie (a). L'auto-inductance par unité de longueur est déterminée sur la base de ce résultat et de l'équation \ ref {14.22}.

Solution

Nous déterminons le champ magnétique entre les conducteurs en appliquant la loi d'Ampère à la trajectoire circulaire en pointillés illustrée sur la figure\(\PageIndex{1b}\). En raison de la symétrie cylindrique,\(\vec{B}\) est constante le long du trajet, et\[\oint \vec{B} \cdot d\vec{l} = B(2\pi r) = \mu_0 I.\] cela nous donne\[B = \dfrac{\mu_0I}{2\pi r}. \nonumber\] Dans la région située à l'extérieur du câble, une application similaire de la loi d'Ampère montre que\(B = 0\), puisqu'aucun courant net ne traverse la zone délimitée par un trajet circulaire où\(r > R_2\). Cet argument vaut également quand, c'\(r < R_1\)est-à-dire dans la région située à l'intérieur du cylindre intérieur. Toute l'énergie magnétique du câble est donc stockée entre les deux conducteurs. Puisque la densité d'énergie du champ magnétique est\[u_m = \dfrac{B^2}{2\mu_0}\nonumber\] l'énergie stockée dans une enveloppe cylindrique de rayon intérieur r, de rayon extérieur\(r + dr\) et de longueur l (voir la partie (c) de la figure) est\[u_m = \dfrac{\mu_0I^2}{8\pi^2 r^2}.\nonumber\] donc, l'énergie totale du champ magnétique sur une longueur l de le câble est\[U = \int_{R_1}^{R_2} dU = \int_{R_1}^{R_2} \dfrac{\mu_0I^2}{8\pi^2r^2}(2\pi rl)dr = \dfrac{\mu_0I^2l}{4\pi} ln \dfrac{R_2}{R_1},\nonumber\] et l'énergie par unité de longueur est\((\mu_0I^2 / 4\pi)ln(R_2/R_1).\)
À partir de l'équation \ ref {14.22},\[U = \dfrac{1}{2}LI^2,\] où L est l'auto-inductance d'une longueur l du câble coaxial. En assimilant les deux équations précédentes, nous trouvons que l'auto-inductance par unité de longueur du câble est\[\dfrac{L}{l} = \dfrac{\mu_0}{2\pi}\ln\dfrac{R_2}{R_1}.\nonumber\]

L'importance

L'inductance par unité de longueur dépend uniquement des rayons intérieur et extérieur, comme le montre le résultat. Pour augmenter l'inductance, nous pouvons soit augmenter le rayon extérieur (\(R_2\)), soit diminuer le rayon intérieur (\(R_1\)). Dans la limite où les deux rayons deviennent égaux, l'inductance passe à zéro. Dans cette limite, il n'y a pas de câble coaxial. De plus, l'énergie magnétique par unité de longueur provenant de la partie (a) est proportionnelle au carré du courant.

Exercice\(\PageIndex{1}\)

Quelle quantité d'énergie est stockée dans l'inducteur de l'exemple 14.3.1 une fois que le courant a atteint sa valeur maximale ?

Solution: 0,50 M