13.4 : Emf émotionnel
- Page ID
- 191064
À la fin de cette section, vous serez en mesure de :
- Déterminer l'amplitude d'une force électromotrice induite dans un fil se déplaçant à vitesse constante dans un champ magnétique
- Discutez d'exemples qui utilisent des forces électromagnétiques émotionnelles, comme un canon à rail et un satellite captif
Le flux magnétique dépend de trois facteurs : l'intensité du champ magnétique, la zone traversée par les lignes de champ et l'orientation du champ par rapport à la surface. Si l'une de ces quantités varie, une variation correspondante du flux magnétique se produit. Jusqu'à présent, nous n'avons pris en compte que les changements de flux dus à un champ changeant. Nous examinons maintenant une autre possibilité : une zone changeante à travers laquelle passent les lignes de champ, y compris un changement d'orientation de la zone.
Deux exemples de ce type de changement de flux sont représentés sur la figure\(\PageIndex{1}\). Dans la partie (a), le flux à travers la boucle rectangulaire augmente à mesure qu'elle se déplace dans le champ magnétique, et dans la partie (b), le flux à travers la bobine rotative varie avec l'angle\(\theta\).
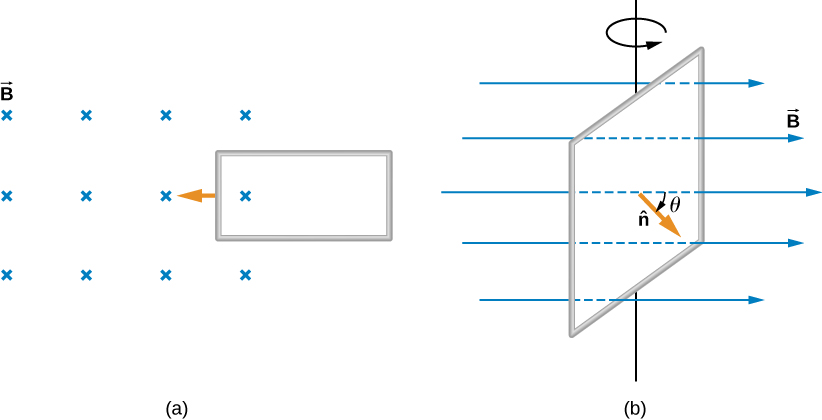
Il est intéressant de noter que ce que nous percevons comme la cause d'un changement de flux particulier dépend en fait du cadre de référence que nous choisissons. Par exemple, si vous êtes au repos par rapport aux bobines mobiles de la Figure\(\PageIndex{1b}\), vous verrez le flux varier en raison de la modification du champ magnétique : dans la partie (a), le champ se déplace de gauche à droite dans votre repère de référence, et dans la partie (b), le champ est en rotation. Il est souvent possible de décrire un changement de flux à travers une bobine qui se déplace dans un référentiel particulier en termes de champ magnétique changeant dans un second cadre, où la bobine est stationnaire. Cependant, les questions du cadre de référence liées au flux magnétique dépassent le niveau de ce manuel. Nous éviterons de telles complexités en travaillant toujours dans un cadre au repos par rapport au laboratoire et en expliquant les variations de flux comme étant dues à un champ ou à une zone changeante.
Regardons maintenant une tige conductrice entraînée dans un circuit et modifiant le flux magnétique. La zone délimitée par le circuit « MNOP » de la figure\(\PageIndex{2}\) est lx et est perpendiculaire au champ magnétique, ce qui nous permet de simplifier l'intégration de\(\Phi_{\mathrm{m}}=\int_{S} \overrightarrow{\mathbf{B}} \cdot \hat{\mathbf{n}} d A\) dans une multiplication du champ magnétique et de la surface. Le flux magnétique à travers la surface ouverte est donc
\[\Phi_m = Blx.\]
Puisque B et l sont constants et que la vitesse de la tige l'est\(v = dx/dt\), nous pouvons maintenant reformuler la loi de Faraday, Équation 13.2.2, pour l'amplitude de la force électromotrice en termes de tige conductrice en mouvement comme
\[\epsilon = \frac{d\Phi_m}{dt} = Bl \frac{dx}{dt} = Blv.\]
Le courant induit dans le circuit est la force électromotrice divisée par la résistance ou
\[I = \frac{Blv}{R}.\]
De plus, la direction de la force électromotrice induite est conforme à la loi de Lenz, comme vous pouvez le vérifier en inspectant la figure.
Ce calcul de la force électromotrice induite par le mouvement ne se limite pas à une tige se déplaçant sur des rails conducteurs. Avec\(\vec{F} = q\vec{v} \times \vec{B}\) comme point de départ, on peut montrer que tout changement de flux provoqué par le mouvement d'un conducteur est\(\epsilon = - d\Phi_m/dt\) valable. Nous avons vu dans la loi de Faraday que la force électromotrice induite par un champ magnétique variant dans le temps obéit à cette même relation, qui est la loi de Faraday. Ainsi, la loi de Faraday s'applique à tous les changements de flux, qu'ils soient produits par un champ magnétique changeant, par un mouvement ou par une combinaison des deux.
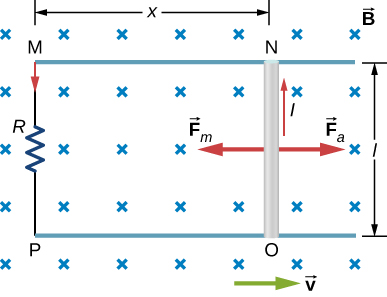
Du point de vue énergétique,\(\vec{F}_a\) produit de l'énergie\(F_a v\) et la résistance dissipe de l'énergie\(I^2R\). Comme la tige se déplace à vitesse constante, la force appliquée\(F_a\) doit équilibrer la force magnétique\(F_m = IlB\) sur la tige lorsqu'elle transporte le courant induit I. Ainsi, la puissance produite est
\[F_av = IlBv = \frac{Blv}{R} \cdot lBv = \frac{l^2B^2v^2}{R}.\]
La puissance dissipée est
\[P = I^2R = \left(\frac{Blv}{R}\right)^2 R = \frac{l^2B^2v^2}{R}.\]
Conformément au principe de conservation de l'énergie, les puissances produites et dissipées sont égales.
Ce principe se retrouve dans le fonctionnement d'un canon à rail. Un canon à rail est un lance-projectiles électromagnétiques qui utilise un appareil similaire à la figure\(\PageIndex{2}\) et est représenté sous forme schématique sur la figure\(\PageIndex{3}\). La tige conductrice est remplacée par un projectile ou une arme à tirer. Jusqu'à présent, nous avons seulement entendu parler de la façon dont le mouvement provoque une force électromotrice. Dans un canon à rail, l'arrêt/la réduction optimale d'un champ magnétique diminue le flux entre les rails, provoquant ainsi la circulation d'un courant dans la tige (armature) qui maintient le projectile. Ce courant traversant l'armature subit une force magnétique et est propulsé vers l'avant. Les canons à rail ne sont toutefois pas largement utilisés dans l'armée en raison du coût de production élevé et des courants élevés : près d'un million d'ampères sont nécessaires pour produire suffisamment d'énergie pour qu'un canon à rail soit une arme efficace.
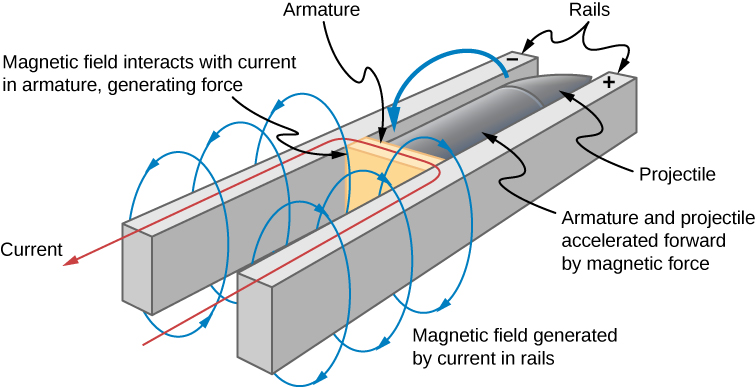
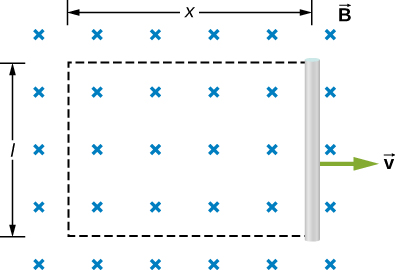
Nous pouvons calculer une force électromotrice induite par les mouvements avec la loi de Faraday même en l'absence d'un véritable circuit fermé. Nous imaginons simplement une zone fermée dont la limite inclut le conducteur en mouvement, calculons\(\Phi_m\), puis trouvons la force électromotrice à partir de la loi de Faraday. Par exemple, nous pouvons laisser la barre mobile de la Figure\(\PageIndex{4}\) se trouver sur un côté de la zone rectangulaire imaginaire représentée par les lignes pointillées. L'aire du rectangle est lx, donc le flux magnétique qui le traverse l'est\(\Phi_m = Blx\). En différenciant cette équation, nous obtenons
\[\frac{d\Phi_m}{dt} = Bl\frac{dx}{dt} = Blv,\]
qui est identique à la différence de potentiel entre les extrémités de la tige que nous avons déterminée précédemment.
Les champs magnétiques du faible champ magnétique de la Terre ne sont généralement pas très importants, ou nous remarquerons une tension le long de tiges métalliques, comme un tournevis, lors de mouvements ordinaires. Par exemple, un simple calcul de la force électromotrice d'une tige de 1,0 m se déplaçant à 3,0 m/s perpendiculairement au champ terrestre donne
\[emf = Blv = (5.0 \times 10^{-5} T)(1.0 \, m)(3.0 \, m/s) = 150 \, \mu V.\]
Cette faible valeur est conforme à l'expérience. Il existe cependant une exception spectaculaire. En 1992 et 1996, des tentatives ont été faites avec la navette spatiale pour créer de grandes forces électromagnétiques émotionnelles. Le satellite captif devait être lancé sur un fil de 20 km de long, comme le montre la figure\(\PageIndex{5}\), pour créer une force électromotrice de 5 kV en se déplaçant à une vitesse orbitale dans le champ terrestre. Cette force électromotrice pourrait être utilisée pour convertir une partie de l'énergie cinétique et potentielle de la navette en énergie électrique si un circuit complet pouvait être réalisé. Pour compléter le circuit, l'ionosphère stationnaire devait fournir un chemin de retour par lequel le courant pouvait circuler. (L'ionosphère est l'atmosphère raréfiée et partiellement ionisée aux altitudes orbitales. Il conduit à cause de l'ionisation. L'ionosphère remplit la même fonction que les rails fixes et la résistance de connexion de la figure\(\PageIndex{3}\), sans lesquels il n'y aurait pas de circuit complet.) Le\(F = IlBsin \, \theta\) fait de faire glisser le courant dans le câble en raison de la force magnétique permet de réduire l'énergie cinétique et potentielle de la navette et de la convertir en énergie électrique. Les deux tests ont échoué. Dans le premier cas, le câble était suspendu et ne pouvait être prolongé que de quelques centaines de mètres ; dans le second, le câble s'est cassé lorsqu'il était presque complètement étendu. L'exemple\(\PageIndex{1}\) indique la faisabilité en principe.
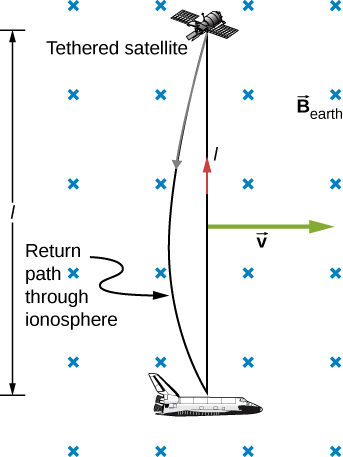
Calculez la force électromotrice induite le long d'un conducteur de 20,0 km se déplaçant à une vitesse orbitale de 7,80 km/s perpendiculaire au champ\(5.00 \times 10^{-5} T\) magnétique de la Terre.
Stratégie
C'est un excellent exemple d'utilisation de l'équation motionnelle\(\epsilon = Blv\).
Solution
La saisie des valeurs données dans\(\epsilon = Blv\) donne
\[\epsilon = Blv\]
\[= (5.00 \times 10^{-5}T)(2.00 \times 10^4 \, m)(7.80 \times 10^3 \, m/s)\]
\[= 7.80 \times 10^3 \, V.\]
L'importance
La valeur obtenue est supérieure à la tension de 5 kV mesurée pour l'expérience de la navette, car le mouvement orbital réel de l'attache n'est pas perpendiculaire au champ terrestre. La valeur de 7,80 kV est la force électromotrice maximale obtenue quand\(\theta = 90^o\) et ainsi de suite\(sin \, \theta = 1\).
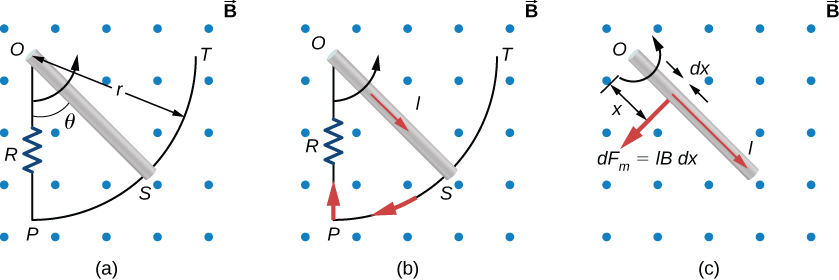
La partie (a) de la figure\(\PageIndex{6}\) montre une tige métallique OS qui tourne dans un plan horizontal autour du point O. La tige glisse le long d'un fil qui forme un arc de cercle PST de rayon r. Le système est soumis à un champ magnétique constant\(\vec{B}\) qui est dirigé hors de la page. (a) Si vous faites tourner la tige à une vitesse angulaire constante\(\omega\), quel est le courant I dans l'OPSO en boucle fermée ? Supposons que la résistance R fournit toute la résistance de la boucle fermée. (b) Calculez le travail par unité de temps que vous effectuez lors de la rotation de la tige et montrez qu'il est égal à la puissance dissipée dans la résistance.
Stratégie
Le flux magnétique est le champ magnétique multiplié par l'aire du quart de cercle ou\(A = r^2 \theta/2\). Lorsque vous déterminez la force électromotrice par la loi de Faraday, toutes les variables sont constantes dans le temps mais\(\theta\), avec\(\omega = d\theta/dt\). Pour calculer le travail par unité de temps, nous savons que cela est lié au couple multiplié par la vitesse angulaire. Le couple est calculé en connaissant la force exercée sur une tige et en l'intégrant sur la longueur de la tige.
Solution
- D'après la géométrie, l'aire de la boucle OPSO est\(A = \frac{r^2\theta}{2}\). Par conséquent, le flux magnétique à travers la boucle se\[\Phi_m = BA = B\frac{r^2\theta}{2}.\] différencie en fonction du temps et en utilisant\(\omega = d\theta/dt\), nous avons :\[\epsilon = \left|\frac{d\Phi_m}{dt}\right| = \frac{Br^2\omega}{2}.\] lorsqu'il est divisé par la résistance R de la boucle, cela donne l'amplitude du courant induit As\(\theta\) augmente, de\[I = \frac{\epsilon}{R} = \frac{Br^2\omega}{2R}.\] même que le flux à travers la boucle due à\(\vec{B}\). Pour compenser cette augmentation, le champ magnétique dû au courant induit doit être dirigé vers la page dans la zone délimitée par la boucle. Par conséquent, comme l'\(\PageIndex{6}\)illustre la partie (b) de la figure, le courant circule dans le sens des aiguilles d'une montre.
- Vous faites tourner la tige en exerçant un couple sur celle-ci. Comme la tige tourne à vitesse angulaire constante, ce couple est égal et opposé au couple exercé sur le courant dans la tige par le champ magnétique d'origine. La force magnétique sur le segment infinitésimal de longueur dx illustrée dans la partie (c) de la figure\(\PageIndex{6}\) est\(dF_m = IBdx\), donc le couple magnétique sur ce segment est\[d\tau_m = x \cdot dF_m = IBxdx.\] Le couple magnétique net sur la tige est alors\[\tau_m = \int_0^r d\tau_m = IB \int_0^r x \, dx = \frac{1}{2}IBr^2.\] Le couple\(\tau\) que vous exercez sur la tige est égal et opposé à \(\tau_m\), et le travail que vous effectuez lorsque la tige tourne d'un angle\(d\theta\) est\(dW = rd\theta\). Par conséquent, le travail par unité de temps que vous effectuez sur la tige\[\frac{dW}{dt} = \tau\frac{d\theta}{dt} = \frac{1}{2} IBr^2 \frac{d\theta}{dt} = \frac{1}{2} \left(\frac{Br^2\omega}{2R}\right) Br^2\omega = \frac{B^2r^4\omega^2}{4R},\] est celui que nous avons remplacé moi. La puissance dissipée dans la résistance est\(P = IR^2\), qui peut être écrite comme suit :\[P = \left(\frac{Br^2\omega}{2R}\right)^2 R = \frac{B^2r^4\omega^2}{4R}.\] Par conséquent, nous voyons que, par\[P = \frac{dW}{dt}.\] conséquent, la puissance dissipée dans la résistance est égale au travail par unité de temps effectué pour faire tourner la tige.
L'importance
Une autre façon d'examiner la force électromotrice induite par la loi de Faraday est de l'intégrer dans l'espace plutôt que dans le temps. La solution serait toutefois la même. L'emf émotionnel est
\[|\epsilon| = \int Bvdl.\]
La vitesse peut être écrite comme la vitesse angulaire multipliée par le rayon et la longueur différentielle écrite sous la forme dr. Par conséquent,
\[\epsilon| = B\int vdr = B\omega \int_0^l rdr = \frac{1}{2} B\omega l^2,\]ce qui est la même solution que précédemment.
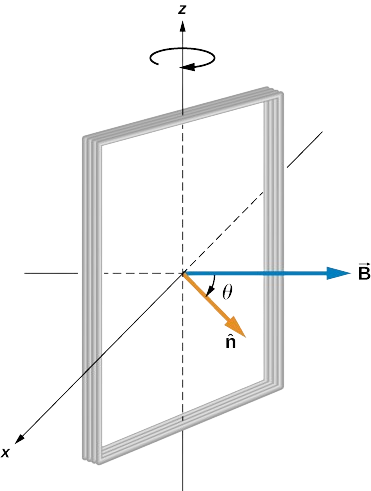
Une bobine rectangulaire de spires de zone A et N est placée dans un champ magnétique uniforme\(\vec{B} = B\hat{j}\), comme le montre la figure\(\PageIndex{7}\). La bobine tourne autour de l'axe z à travers son centre à une vitesse angulaire constante\(\omega\). Obtenez une expression de la force électromotrice induite dans la bobine.
Stratégie
Selon le schéma, l'angle entre la perpendiculaire à la surface ((\ hat {n} \)) et le champ magnétique\((\vec{B})\) est de\(\theta\). Le produit scalaire de\(B \cdot \hat{n}\) simplifie uniquement la\(cos \, \theta\) composante du champ magnétique, à savoir l'endroit où le champ magnétique se projette sur le vecteur de surface unitaire\(\hat{n}\). L'amplitude du champ magnétique et la surface de la boucle sont fixes dans le temps, ce qui simplifie rapidement l'intégration. La force électromotrice induite est écrite selon la loi de Faraday.
Solution
Lorsque la bobine est dans une position telle que son vecteur normal forme\(\hat{n}\) un angle\(\theta\) avec le champ magnétique,\(\vec{B}\) le flux magnétique à travers une seule spire de la bobine est
\[\Phi_m = \int_S \vec{B} \cdot \hat{n} dA = BA \, cos \, \theta.\]
D'après la loi de Faraday, la force électromotrice induite dans la bobine est
\[\epsilon = - N\frac{d\Phi_m}{dt} = NB A \, sin \, \theta \frac{d\theta}{dt}.\]
La vitesse angulaire constante est\(\omega = d\theta /dt\). L'angle\(\theta\) représente l'évolution dans le temps de la vitesse angulaire ou\(\omega t\). Cela change la fonction en espace temporel plutôt que\(\theta\). La force électromoïde induite varie donc de manière sinusoïdale avec le temps en fonction de
\[\epsilon = \epsilon_0 \, sin \, \omega t,\]où\(\epsilon_0 = NBA \omega\).
L'importance
Si l'intensité du champ magnétique ou la surface de la boucle changeaient également au fil du temps, ces variables ne pourraient pas être extraites de la dérivée temporelle pour simplement obtenir la solution, comme indiqué. Cet exemple constitue la base d'un générateur électrique, car nous en donnerons une discussion complète dans Applications de la loi de Newton.
La figure ci-dessous montre une tige de longueur l qui tourne dans le sens antihoraire autour de l'axe passant par O sous l'effet du couple dû à\(m\vec{g}\). En supposant que la tige se trouve dans un champ magnétique uniforme\(\vec{B}\), quelle est la force électromotrice induite entre les extrémités de la tige lorsque sa vitesse angulaire est égale à\(\omega\) ? Quelle extrémité de la tige présente le potentiel le plus élevé ?
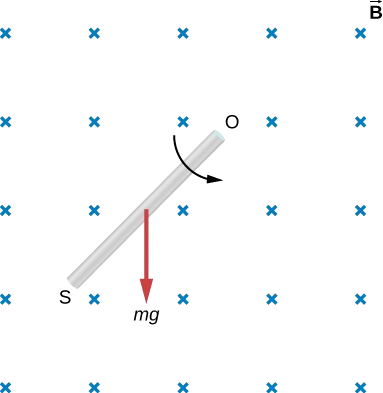
- Réponse
-


