13.3 : Loi de Lenz

Objectifs d'apprentissage

À la fin de cette section, vous serez en mesure de :

• Utilisez la loi de Lenz pour déterminer la direction de la force électromotrice induite chaque fois qu'un flux magnétique change
• Utilisez la loi de Faraday avec la loi de Lenz pour déterminer la force électromotrice induite dans une bobine et dans un solénoïde

La direction dans laquelle la force électromotrice induite entraîne le courant autour d'une boucle de fil peut être déterminée par le signe négatif. Cependant, il est généralement plus facile de déterminer cette direction avec la loi de Lenz, nommée en l'honneur de son découvreur, Heinrich Lenz (1804-1865). (Faraday a également découvert cette loi, indépendamment de Lenz.) Nous énonçons la loi de Lenz comme suit :

Loi de Lenz

La direction de la force électromotrice induite fait circuler le courant autour d'une boucle de fil afin de toujours s'opposer à la modification du flux magnétique qui provoque la force électromotrice.

La loi de Lenz peut également être considérée en termes de conservation de l'énergie. Si le fait d'enfoncer un aimant dans une bobine produit du courant, l'énergie contenue dans ce courant doit provenir de quelque part. Si le courant induit provoque un champ magnétique qui s'oppose à l'augmentation du champ de l'aimant dans lequel nous avons poussé, alors la situation est claire. Nous avons poussé un aimant contre un champ et avons travaillé sur le système, et cela s'est traduit par du courant. S'il n'était pas vrai que le champ induit s'oppose à la modification du flux, l'aimant serait attiré pour produire un courant sans que rien n'ait fonctionné. De l'énergie potentielle électrique aurait été créée, violant ainsi la conservation de l'énergie.

Pour déterminer une force électromotrice induite\(\epsilon\), vous devez d'abord calculer le flux magnétique,\(\Phi_m\) puis obtenir\(d\Phi_m/dt\). La magnitude de\(\epsilon\) est donnée par

\[\epsilon = \left|\dfrac{d\Phi_m}{dt}\right|.\]

Enfin, vous pouvez appliquer la loi de Lenz pour déterminer le sens de\(\epsilon\). Cela sera développé à l'aide d'exemples illustrant la stratégie de résolution de problèmes suivante.

Stratégie de résolution de problèmes : la loi de Lenz

Pour utiliser la loi de Lenz afin de déterminer les directions des champs magnétiques induits, des courants et des champs électromagnétiques :

• Faites un croquis de la situation à utiliser pour visualiser et enregistrer les directions.
• Déterminez la direction du champ magnétique appliqué\(\vec{B}\).
• Déterminez si son flux magnétique augmente ou diminue.
• Déterminez maintenant la direction du champ magnétique induit\(\vec{B}\). Le champ magnétique induit cherche à renforcer un flux magnétique qui diminue ou s'oppose à un flux magnétique qui augmente. Par conséquent, le champ magnétique induit s'ajoute ou se soustrait au champ magnétique appliqué, en fonction de la variation du flux magnétique.
• Utilisez la règle 2 de la main droite (RHR-2 ; voir Forces et champs magnétiques) pour déterminer la direction du courant induit I responsable du champ magnétique induit\(\vec{B}\).
• La direction (ou polarité) de la force électromotrice induite peut désormais entraîner un courant conventionnel dans cette direction.

Appliquons la loi de Lenz au système de Figure\(\PageIndex{1a}\). Nous désignons « l'avant » de la boucle conductrice fermée comme la région contenant le barreau magnétique qui approche, et le « dos » de la boucle comme l'autre région. Lorsque le pôle nord de l'aimant se déplace vers la boucle, le flux à travers la boucle dû au champ de l'aimant augmente en raison de l'intensité des lignes de champ dirigées de l'avant vers l'arrière de la boucle. Un courant est donc induit dans la boucle. Selon la loi de Lenz, la direction du courant induit doit être telle que son propre champ magnétique soit dirigé de manière à s'opposer à la modification du flux provoquée par le champ de l'aimant qui approche. Ainsi, le courant induit circule de telle sorte que ses lignes de champ magnétique à travers la boucle soient dirigées de l'arrière vers l'avant de la boucle. À l'aide du RHR-2, placez votre pouce pointé contre les lignes de champ magnétique, qui sont dirigées vers le barreau magnétique. Vos doigts s'enroulent dans le sens antihoraire, vu depuis le barreau magnétique. Alternativement, nous pouvons déterminer la direction du courant induit en traitant la boucle de courant comme un électroaimant qui s'oppose à l'approche du pôle nord du barreau magnétique. Cela se produit lorsque le courant induit circule comme indiqué, car alors la face de la boucle la plus proche de l'aimant qui approche est également un pôle nord.

Figure\(\PageIndex{1}\) : La modification du flux magnétique provoquée par l'approche de l'aimant induit un courant dans la boucle. (a) L'approche d'un pôle nord induit un courant dans le sens antihoraire par rapport au barreau magnétique. (b) L'approche d'un pôle sud induit un courant dans le sens des aiguilles d'une montre par rapport au barreau magnétique.

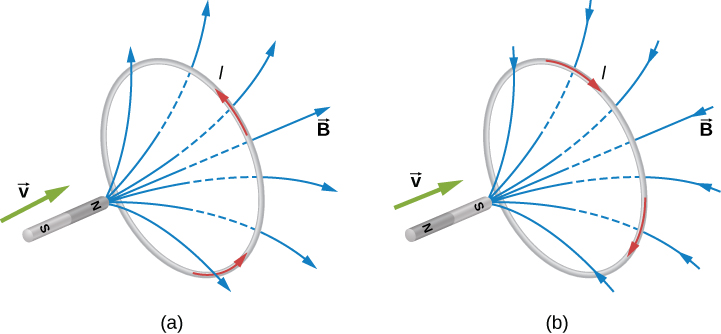
La partie (b) de la figure montre le pôle sud d'un aimant se déplaçant vers une boucle conductrice. Dans ce cas, le flux à travers la boucle dû au champ de l'aimant augmente car le nombre de lignes de champ dirigées de l'arrière vers l'avant de la boucle augmente. Pour s'opposer à ce changement, un courant est induit dans la boucle dont les lignes de champ à travers la boucle sont dirigées de l'avant vers l'arrière. De manière équivalente, on peut dire que le courant circule dans une direction telle que la face de la boucle la plus proche de l'aimant qui approche est un pôle sud, qui repousse alors le pôle sud approchant de l'aimant. Lorsque vous utilisez le RHR-2, votre pouce pointe à l'opposé de la barre magnétique. Vos doigts s'enroulent dans le sens des aiguilles d'une montre, c'est-à-dire la direction du courant induit.

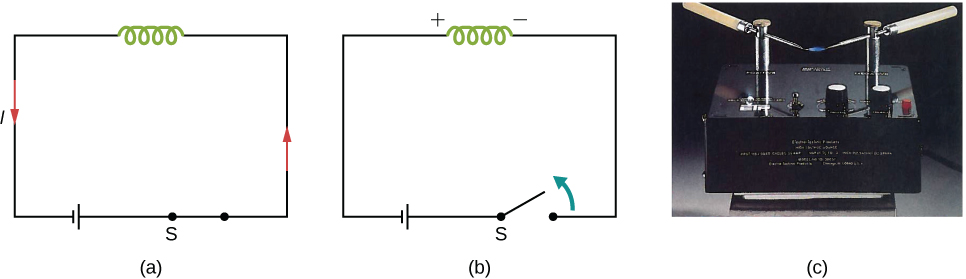
Un autre exemple illustrant l'utilisation de la loi de Lenz est illustré dans la figure\(\PageIndex{2}\). Lorsque l'interrupteur est ouvert, la diminution du courant traversant le solénoïde entraîne une diminution du flux magnétique à travers ses bobines, ce qui induit une force électromotrice dans le solénoïde. Cette force électromotrice doit s'opposer au changement (la fin du courant) qui la provoque. Par conséquent, la force électromotrice induite a la polarité indiquée et se déplace dans la direction du courant d'origine. Cela peut générer un arc aux bornes du commutateur lorsqu'il est ouvert.

Figure\(\PageIndex{2}\) : (a) Un solénoïde connecté à une source de force électromotrice. (b) L'ouverture de l'interrupteur S met fin au courant, qui à son tour induit une force électromotrice dans le solénoïde. (c) Une différence de potentiel entre les extrémités des tiges pointues est produite en induisant une force électromotrice dans une bobine. Cette différence de potentiel est suffisamment grande pour produire un arc entre les pointes pointues.

Exercice\(\PageIndex{1A}\)

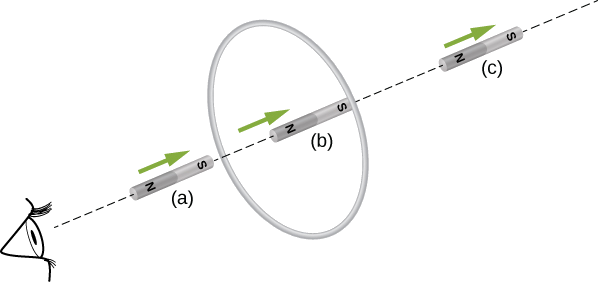
Déterminez la direction du courant induit dans la boucle de fil illustrée ci-dessous lorsque l'aimant entre, traverse et quitte la boucle.

Solution

Pour l'observateur représenté, le courant circule dans le sens des aiguilles d'une montre lorsque l'aimant s'approche, diminue jusqu'à zéro lorsque l'aimant est centré dans le plan de la bobine, puis circule dans le sens antihoraire lorsque l'aimant quitte la bobine.

Exercice\(\PageIndex{1B}\)

Verify the directions of the induced currents in Figure 13.2.2.

Example \(\PageIndex{1A}\): A Circular Coil in a Changing Magnetic Field

A magnetic field \(\vec{B}\) is directed outward perpendicular to the plane of a circular coil of radius \(r = 0.50 \, m\) (Figure \(\PageIndex{3}\)). The field is cylindrically symmetrical with respect to the center of the coil, and its magnitude decays exponentially according to \(B = (1.5T)e^{(5.0s^{-1})t}\), where B is in teslas and t is in seconds. (a) Calculate the emf induced in the coil at the times \(t_1 = 0\), \(t_2 = 5.0 \times 10^{-2}s\), and \(t_3 = 1.0 \, s\). (b) Determine the current in the coil at these three times if its resistance is \(10 \, \Omega\).

Figure \(\PageIndex{3}\): A circular coil in a decreasing magnetic field.

Strategy

Since the magnetic field is perpendicular to the plane of the coil and constant over each spot in the coil, the dot product of the magnetic field \(\vec{B}\) and normal to the area unit vector \(\hat{n}\) turns into a multiplication. The magnetic field can be pulled out of the integration, leaving the flux as the product of the magnetic field times area. We need to take the time derivative of the exponential function to calculate the emf using Faraday’s law. Then we use Ohm’s law to calculate the current.

Solution

1. Since \(\vec{B}\) is perpendicular to the plane of the coil, the magnetic flux is given by \[\Phi_m = B\pi r^2 = (1.5 e^{-5.0 t}T)\pi (0.50 \, m)^2\]\[= 1.2 e^{-(5.0 s^{-1})t} Wb.\] From Faraday’s law, the magnitude of the induced emf is \[\epsilon = \left|\frac{d\Phi_m}{dt}\right| = \left|\frac{d}{dt} (1.2 e^{-(5.0s^{-1})t} Wb)\right| = 6.0 e^{-(5.0s^{-1})t}V.\] Since \(\vec{B}\) is directed out of the page and is decreasing, the induced current must flow counterclockwise when viewed from above so that the magnetic field it produces through the coil also points out of the page. For all three times, the sense of ε is counterclockwise; its magnitudes are \[\epsilon (t_1) = 6.0 V; \, \epsilon (t_2) = 4.7 \, V; \, \epsilon (t_3) = 0040 \, V.\]
2. From Ohm’s law, the respective currents are \[I(t_1) = \frac{\epsilon (t_1)}{R} = \frac{6.0 \, V}{10 \, \Omega} = 0.60 \, A;\]\[I(t_2) = \frac{4.7 \, V}{10 \, \Omega} = 0.47 \, A;\] and \[I(t_3) = \frac{0.040 \, V}{10 \, \Omega} = 4.0 \times 10^{-3} \, A.\]

Significance

An emf voltage is created by a changing magnetic flux over time. If we know how the magnetic field varies with time over a constant area, we can take its time derivative to calculate the induced emf.

Example \(\PageIndex{1B}\): Changing Magnetic Field Inside a Solenoid

The current through the windings of a solenoid with \(n = 2000\) turns per meter is changing at a rate \(dI/dt = 3.0 \, A/s\). (See Sources of Magnetic Fields for a discussion of solenoids.) The solenoid is 50-cm long and has a cross-sectional diameter of 3.0 cm. A small coil consisting of \(N = 20\) closely wound turns wrapped in a circle of diameter 1.0 cm is placed in the middle of the solenoid such that the plane of the coil is perpendicular to the central axis of the solenoid. Assuming that the infinite-solenoid approximation is valid at the location of the small coil, determine the magnitude of the emf induced in the coil.

Strategy

The magnetic field in the middle of the solenoid is a uniform value of \(\mu_0 nI\). This field is producing a maximum magnetic flux through the coil as it is directed along the length of the solenoid. Therefore, the magnetic flux through the coil is the product of the solenoid’s magnetic field times the area of the coil. Faraday’s law involves a time derivative of the magnetic flux. The only quantity varying in time is the current, the rest can be pulled out of the time derivative. Lastly, we include the number of turns in the coil to determine the induced emf in the coil.

Solution

Since the field of the solenoid is given by \(B = \mu_0 nI\), the flux through each turn of the small coil is \[\Phi_m = \mu_0 nI\left(\frac{\pi d^2}{4}\right),\]

where d is the diameter of the coil. Now from Faraday’s law, the magnitude of the emf induced in the coil is

\[\epsilon = \left|N\frac{d\Phi_m}{dt}\right| = \left|N\mu_0 n\frac{\pi d^2}{4} \frac{dI}{dt}\right|\]

\[= 20 (4\pi \times 10^{-7} T \cdot m/s)(2000 \, m^{-1}) \frac{\pi(0.010 \, m)^2}{4} (3.0 \, A/s)\]\[= 1.2 \times 10^{-5} \, V.\]

Significance

When the current is turned on in a vertical solenoid, as shown in Figure \(\PageIndex{4}\), the ring has an induced emf from the solenoid’s changing magnetic flux that opposes the change. The result is that the ring is fired vertically into the air.

Figure \(\PageIndex{4}\): The jumping ring. When a current is turned on in the vertical solenoid, a current is induced in the metal ring. The stray field produced by the solenoid causes the ring to jump off the solenoid.

Note

A demonstration of the jumping ring from MIT.