13.5 : Champs électriques induits
- Page ID
- 191072
À la fin de cette section, vous serez en mesure de :
- Reliez la relation entre une force électromotrice induite par la loi de Faraday et un champ électrique, montrant ainsi qu'un flux magnétique changeant crée un champ électrique
- Résolvez le champ électrique en fonction de l'évolution du flux magnétique dans le temps
Le fait que les champs électromagnétiques soient induits dans les circuits implique que l'on travaille sur les électrons de conduction dans les fils. Quelle peut être la source de ce travail ? Nous savons qu'il ne s'agit ni d'une batterie ni d'un champ magnétique, car une batterie n'a pas besoin d'être présente dans un circuit où le courant est induit, et les champs magnétiques ne fonctionnent jamais sur des charges mobiles. La réponse est que la source de l'œuvre est un champ\(\vec{E}\) électrique induit dans les fils. Le travail effectué\(\vec{E}\) en déplaçant complètement une charge unitaire autour d'un circuit est la force électromotrice induite\(ε\), c'est-à-dire
\[\epsilon = \oint \vec{E} \cdot d\vec{l},\]où\(\oint\) représente l'intégrale de la ligne autour du circuit. La loi de Faraday peut être écrite en termes de champ électrique induit comme
\[\oint \vec{E} \cdot d\vec{l} = - \dfrac{d\Phi_m}{dt}.\]
Il existe une distinction importante entre le champ électrique induit par un champ magnétique changeant et le champ électrostatique produit par une distribution de charge fixe. Plus précisément, le champ électrique induit n'est pas conservateur car il agit en réseau en déplaçant une charge sur un trajet fermé, alors que le champ électrostatique est conservateur et ne fonctionne pas sur un trajet fermé. Ainsi, le potentiel électrique peut être associé au champ électrostatique, mais pas au champ induit. Les équations suivantes représentent la distinction entre les deux types de champ électrique :
\[ \underbrace{\oint \vec{E} \cdot d\vec{l} \neq 0}_{\text{Induced Electric Field}}\]
\[\underbrace{ \oint \vec{E} \cdot d\vec{l} = 0}_{\text{Electrostatic Electric Fields}}.\]
Nos résultats peuvent être résumés en combinant les équations suivantes :
\[\epsilon = \oint \vec{E} \cdot d\vec{l} = - \dfrac{d\Phi_m}{dt}. \label{eq5}\]
Quel est le champ électrique induit dans la bobine circulaire de l'exemple 13.3.1A (et de la Figure 13.3.3) aux trois heures indiquées ?
Stratégie
En utilisant la symétrie cylindrique, l'intégrale du champ électrique se simplifie en champ électrique multiplié par la circonférence d'un cercle. Comme nous connaissons déjà la force électromotrice induite, nous pouvons relier ces deux expressions par la loi de Faraday pour résoudre le champ électrique induit.
Solution
Le champ électrique induit dans la bobine est d'une amplitude constante sur la surface cylindrique, de la même manière que les problèmes liés à la loi d'Ampère avec les cylindres sont résolus. Comme\(\vec{E}\) il est tangent à la bobine,
\[\oint \vec{E} \cdot d\vec{l} = \oint E dl = 2 \pi r E. \nonumber\]
Combiné à l'équation \ ref {eq5}, cela donne
\[E = \dfrac{\epsilon}{2\pi r}. \nonumber\]
La direction de\(\epsilon\) est dans le sens antihoraire et\(\vec{E}\) circule dans le même sens autour de la bobine. Les valeurs de E sont
\[ \begin{align*} E(t_1) &= \dfrac{6.0 \, V}{2\pi \, (0.50 \, m)} = 1.9 \, V/m; \\[4pt] E(t_2) &= \dfrac{4.7 \, V}{2\pi \, (0.50 \, m)} = 1.5 \, V/m; \\[4pt] E(t_3) &= \dfrac{0.040 \, V}{2\pi \, (0.50 \, m)} = 0.013 \, V/m; \end{align*}\]
L'importance
Lorsque le flux magnétique à travers un circuit change, un champ électrique non conservateur est induit, qui fait circuler du courant dans le circuit. Mais que se passe-t-il\(dB/dt \neq 0\) dans un espace libre où il n'y a pas de chemin conducteur ? La réponse est que ce cas peut être traité comme si un chemin conducteur était présent ; c'est-à-dire que des champs électriques non conservateurs sont induits partout, qu'il y ait ou\(dB/dt \neq 0\) non un chemin conducteur.
Ces champs électriques non conservateurs satisfont toujours à l'équation \ ref {eq5}. Par exemple, si la bobine circulaire était retirée, un champ électrique dans l'espace libre\(r = 0.50 \, m\) serait toujours dirigé dans le sens antihoraire, et sa magnitude serait toujours de 1,9 V/m à\(t = 0\) 1,5 V/m à\(t = 5.0 \times 10^{-2}s\), etc. L'existence de champs électriques induits ne l'est certainement pas limité aux fils des circuits.
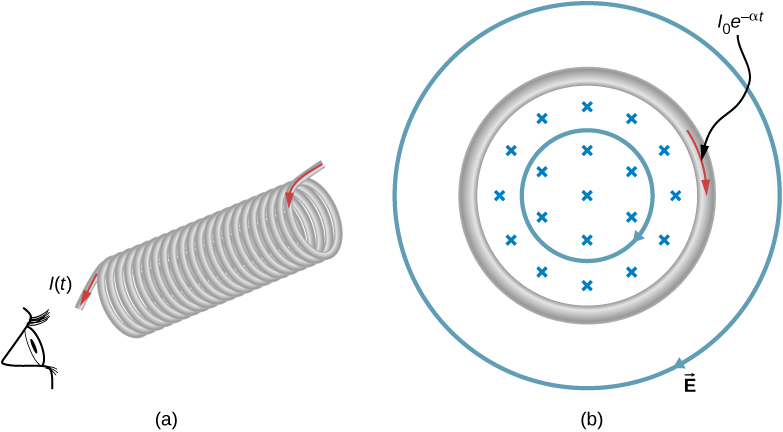
La figure\(\PageIndex{1a}\) montre un solénoïde long avec un rayon R et n tours par unité de longueur ; son courant diminue avec le temps en fonction de\(I = I_0 e^{-\alpha t}\). Quelle est l'amplitude du champ électrique induit en un point situé à une distance r de l'axe central du solénoïde (a) quand\(r > R\) et (b) quand\(r < R\) [Figure\(\PageIndex{1b}\)]. (c) Quelle est la direction du champ induit aux deux endroits ? Supposons que l'approximation du solénoïde infini soit valide dans toutes les régions d'intérêt.
Stratégie
En utilisant la formule du champ magnétique à l'intérieur d'un solénoïde infini et la loi de Faraday, nous calculons la force électromotrice induite. Comme nous avons une symétrie cylindrique, l'intégrale du champ électrique se réduit au champ électrique multiplié par la circonférence du chemin d'intégration. Ensuite, nous résolvons le champ électrique.
Solution
- Le champ magnétique est confiné à l'intérieur du solénoïde où,\[B = \mu_0 nI = \mu_0 n I_0 e^{-\alpha t}.\] ainsi, le flux magnétique à travers un trajet circulaire dont le rayon r est supérieur à R, le rayon du solénoïde, est.\[\Phi_m = BA = \mu_0 n I_0 \pi R^2 e^{-\alpha t}.\] Le champ induit\(\vec{E}\) est tangent à ce trajet, et en raison de la symétrie du système, sa magnitude est constante sur le trajet. Par conséquent, nous avons\[\left| \oint \vec{E} \cdot d\vec{l}\right| = \left|\dfrac{d\Phi_m}{dt}\right|,\]\[E(2\pi r) = \left|\dfrac{d}{dt} (\mu_0 n I_0 \pi R^2 e^{-\alpha t})\right| = \alpha \mu_0 n I_0 \pi R^2 e^{-\alpha t},\]\[E = \dfrac{\alpha \mu_0 n I_0 R^2}{2r} e^{-\alpha t} \, (r > R).\]
- Pour un trajet de rayon r à l'intérieur du solénoïde\(\Phi_m = B\pi r^2\), donc\[E(2\pi) = \left|\dfrac{d}{dt} (\mu_0 n I_0 \pi r^2 e^{-\alpha t})\right| = \alpha \mu_0 n I_0 \pi r^2 e^{-\alpha t},\] et le champ induit est\[ E = \dfrac{\alpha \mu_0 n I_0 r}{2} e^{-\alpha t} \, (r < R).\]
- Le champ magnétique pointe vers la page comme indiqué dans la partie (b) et diminue. Si l'un ou l'autre des chemins circulaires était occupé par des anneaux conducteurs, les courants induits dans ceux-ci circuleraient comme indiqué, conformément à la loi de Lenz. Le champ électrique induit doit également être dirigé de cette manière.
L'importance
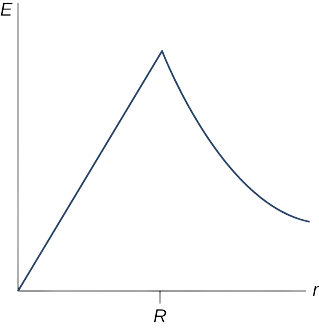
Dans la partie (b), notez que r\(|\vec{E}|\) augmente avec r à l'intérieur et diminue avec 1/ r à l'extérieur du solénoïde, comme indiqué sur la figure\(\PageIndex{2}\).
Supposons que la bobine de l'exemple 13.3.1A soit carrée plutôt que circulaire. L'équation \ ref {eq5} peut-elle être utilisée pour calculer (a) la force électromotrice induite et (b) le champ électrique induit ?
- Réponse
-
a. Oui ; b. Oui ; cependant, il y a un manque de symétrie entre le champ électrique et la bobine, ce qui rend\(\oint \vec{E} \cdot d\vec{l}\) la relation plus complexe qui ne peut être simplifiée, comme le montre l'exemple.
Quelle est l'amplitude du champ électrique induit dans l'exemple\(\PageIndex{2}\) à\(t = 0\) si\(r = 6.0 \, cm\)\(R = 2.0 \, cm\),,\(n = 2000\) tours par mètre\(I_0 = 2.0 \, A\), et\(\alpha = 200 \, s^{-1}\) ?
- Réponse
-
\(3.4 \times 10^{-3} \, V/m\)
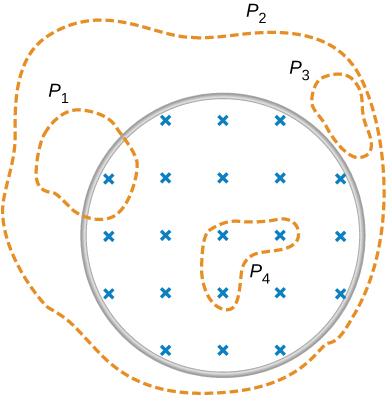
Le champ magnétique illustré ci-dessous est confiné à la région cylindrique représentée et évolue avec le temps. Identifiez les chemins pour lesquels\(\epsilon = \oint \vec{E} \cdot d\vec{l} \neq 0\).
- Réponse
-
\(P_1, \, P_2, \, P_4\)
A long solenoid of cross-sectional area \(5.0 \, cm^2\) is wound with 25 turns of wire per centimeter. It is placed in the middle of a closely wrapped coil of 10 turns and radius 25 cm, as shown below. (a) What is the emf induced in the coil when the current through the solenoid is decreasing at a rate \(dI/dt = -0.20 \, A/s\)? (b) What is the electric field induced in the coil?

- Réponse
-
un.\(3.1 \times 10^{-6} V\); b. \(2.0 \times 10^{-7} \, V/m\)


