11.4 : Mouvement d'une particule chargée dans un champ magnétique

Objectifs d'apprentissage

À la fin de cette section, vous serez en mesure de :

• Expliquer comment une particule chargée dans un champ magnétique externe subit un mouvement circulaire
• Décrire comment déterminer le rayon du mouvement circulaire d'une particule chargée dans un champ magnétique

Une particule chargée subit une force lorsqu'elle se déplace dans un champ magnétique. Que se passe-t-il si ce champ est uniforme pendant le mouvement de la particule chargée ? Quelle est la trajectoire de la particule ? Dans cette section, nous discutons du mouvement circulaire de la particule chargée ainsi que d'autres mouvements résultant de l'entrée d'une particule chargée dans un champ magnétique.

Le cas le plus simple se produit lorsqu'une particule chargée se déplace perpendiculairement à un champ B uniforme (Figure\(\PageIndex{1}\)). Si le champ est dans le vide, le champ magnétique est le facteur dominant qui détermine le mouvement. La force magnétique étant perpendiculaire à la direction de déplacement, une particule chargée suit une trajectoire incurvée dans un champ magnétique. La particule continue de suivre cette trajectoire incurvée jusqu'à former un cercle complet. Une autre façon de voir cela est que la force magnétique est toujours perpendiculaire à la vitesse, de sorte qu'elle n'agit pas sur la particule chargée. L'énergie cinétique et la vitesse de la particule restent donc constantes. La direction du mouvement est affectée, mais pas la vitesse.

Figure\(\PageIndex{1}\) : Une particule chargée négativement se déplace dans le plan du papier dans une région où le champ magnétique est perpendiculaire au papier (représenté par les petites\(X\) particules, comme les queues de flèches). La force magnétique étant perpendiculaire à la vitesse, la vitesse change de direction mais pas d'amplitude. Le résultat est un mouvement circulaire uniforme. (Notez que, comme la charge est négative, la force a une direction opposée à celle de la prédiction de la règle de la main droite.)

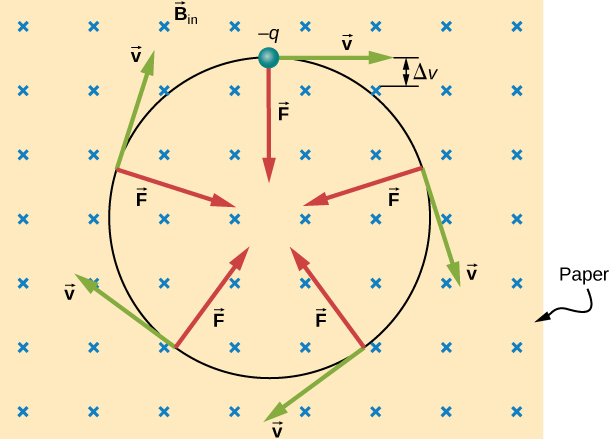
Dans cette situation, la force magnétique fournit la force centripète\(F_C = \dfrac{mv^2}{r}\). En constatant que la vitesse est perpendiculaire au champ magnétique, l'amplitude de la force magnétique est réduite à\(F = qvB\). Parce que la force magnétique F fournit la force centripète\(F_C\), nous avons

\[qvB = \dfrac{mv^2}{r}.\]

Résoudre les problèmes liés aux rendements

\[r = \dfrac{mv}{qB}. \label{11.5}\]

Ici, r est le rayon de courbure de la trajectoire d'une particule chargée de masse m et de charge q, se déplaçant à une vitesse v perpendiculaire à un champ magnétique d'intensité B. Le temps nécessaire à la particule chargée pour parcourir la trajectoire circulaire est défini comme la période, qui est identique à la distance parcourue (la circonférence) divisée par la vitesse. Sur cette base et sur l'équation, nous pouvons déduire la période de mouvement comme

\[T = \dfrac{2\pi r}{v} = \dfrac{2\pi}{v} \dfrac{mv}{qB} = \dfrac{2\pi m}{qB}. \label{11.6}\]

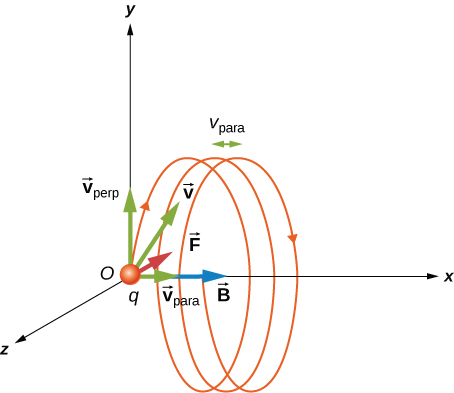
Si la vitesse n'est pas perpendiculaire au champ magnétique, nous pouvons comparer chaque composante de la vitesse séparément avec le champ magnétique. La composante de la vitesse perpendiculaire au champ magnétique produit une force magnétique perpendiculaire à la fois à cette vitesse et au champ :

\[\begin{align} v_{perp} &= v \, \sin \theta \\[4pt] v_{para} &= v \, \cos \theta. \end{align}\]

où\(\theta\) est l'angle entre v et B. La composante parallèle au champ magnétique crée un mouvement constant dans la même direction que le champ magnétique, également illustré dans l'équation. Le mouvement parallèle détermine le pas p de l'hélice, qui est la distance entre les spires adjacentes. Cette distance est égale à la composante parallèle de la vitesse multipliée par la période :

\[p = v_{para} T. \label{11.8}\]

Le résultat est un mouvement hélicoïdal, comme le montre la figure suivante.

Figure\(\PageIndex{2}\) : Une particule chargée se déplaçant à une vitesse différente de celle du champ magnétique. La composante de vitesse perpendiculaire au champ magnétique crée un mouvement circulaire, tandis que la composante de la vitesse parallèle au champ déplace la particule le long d'une ligne droite. Le pitch est la distance horizontale entre deux cercles consécutifs. Le mouvement qui en résulte est hélicoïdal.

Lorsque la particule chargée se déplace sur une trajectoire hélicoïdale, elle peut pénétrer dans une région où le champ magnétique n'est pas uniforme. Supposons en particulier qu'une particule se déplace d'une région de champ magnétique fort vers une région de champ plus faible, puis de nouveau vers une région de champ plus fort. La particule peut être réfléchie avant d'entrer dans la région du champ magnétique le plus fort. Cela ressemble à une vague sur une corde passant d'une ficelle très légère et fine à une paroi dure et se réfléchissant vers l'arrière. Si la réflexion se produit aux deux extrémités, la particule est piégée dans une bouteille dite magnétique.

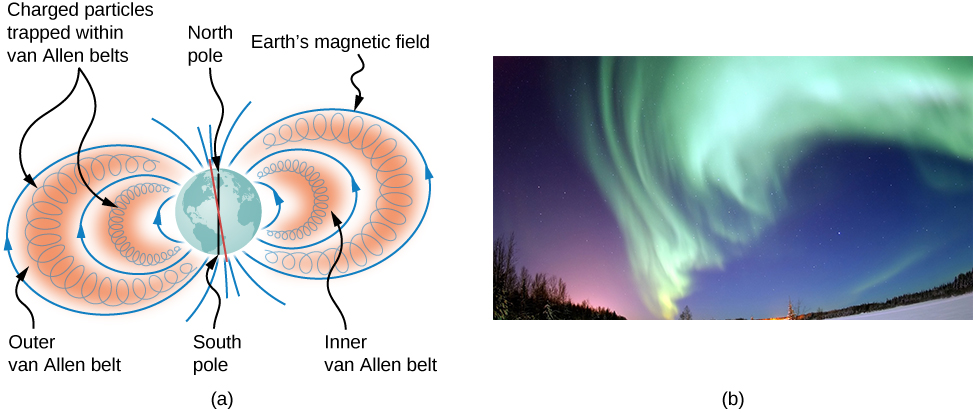
Les particules piégées dans les champs magnétiques se trouvent dans les ceintures de rayonnement de Van Allen autour de la Terre, qui font partie du champ magnétique de la Terre. Ces ceintures ont été découvertes par James Van Allen alors qu'il essayait de mesurer le flux de rayons cosmiques sur Terre (particules de haute énergie provenant de l'extérieur du système solaire) pour voir s'il était similaire au flux mesuré sur Terre. Van Allen a découvert qu'en raison de la contribution des particules piégées dans le champ magnétique de la Terre, le flux était beaucoup plus élevé sur Terre que dans l'espace extra-atmosphérique. Les aurores boréales, comme les célèbres aurores boréales (aurores boréales) de l'hémisphère nord (Figure\(\PageIndex{3}\)), sont de magnifiques images de lumière émise lorsque les ions se recombinent avec les électrons qui pénètrent dans l'atmosphère alors qu'ils spiralent le long des lignes de champ magnétique. (Les ions sont principalement des atomes d'oxygène et d'azote qui sont initialement ionisés par des collisions avec des particules énergétiques dans l'atmosphère de la Terre.) Des aurores ont également été observées sur d'autres planètes, telles que Jupiter et Saturne.

Figure\(\PageIndex{3}\) : (a) Les ceintures de rayonnement de Van Allen qui entourent la Terre retiennent les ions produits par les rayons cosmiques qui frappent l'atmosphère de la Terre. (b) Le magnifique spectacle des aurores boréales, ou aurores boréales, brille dans le ciel nordique au-dessus de Bear Lake, près de la base aérienne d'Eielson, en Alaska. Façonnée par le champ magnétique de la Terre, cette lumière est produite par des molécules incandescentes et des ions d'oxygène et d'azote. (crédit b : modification du travail par Joshua Strang, aviateur senior de l'USAF)

Exemple\(\PageIndex{1}\): Beam Deflector

Un groupe de recherche étudie les isotopes radioactifs à courte durée de vie. Ils doivent concevoir un moyen de transporter les particules alpha (noyaux d'hélium) d'où elles sont fabriquées jusqu'à un endroit où elles entreront en collision avec un autre matériau pour former un isotope. Le faisceau de particules alpha\( (m = 6.64 \times 10^{-27}kg, \, q = 3.2 \times 10^{-19}C)\) se courbe à travers une région de 90 degrés avec un champ magnétique uniforme de 0,050 T (Figure\(\PageIndex{4}\)). a) Dans quelle direction le champ magnétique doit-il être appliqué ? (b) Combien de temps faut-il aux particules alpha pour traverser la région du champ magnétique uniforme ?

Figure\(\PageIndex{4}\) : Vue de dessus de la configuration du déflecteur de faisceau.

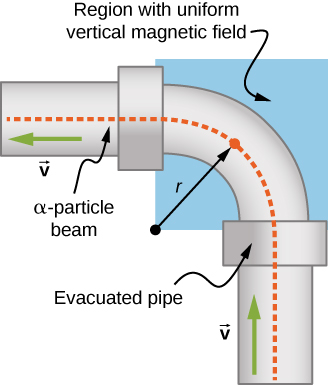
Stratégie

1. La direction du champ magnétique est indiquée par le RHR-1. Vos doigts pointent dans la direction de v et votre pouce doit pointer dans la direction de la force, vers la gauche. Par conséquent, étant donné que les particules alpha sont chargées positivement, le champ magnétique doit pointer vers le bas.
2. La période pendant laquelle la particule alpha fait le tour du cercle est

\[T = \dfrac{2\pi m}{qB}.\]

Comme la particule ne fait que le tour d'un quart de cercle, nous pouvons prendre 0,25 fois plus de temps pour trouver le temps nécessaire pour faire le tour de cette trajectoire.

Solution

1. Commençons par nous concentrer sur la particule alpha qui entre dans le champ en bas de l'image. Commencez par pointer votre pouce vers le haut de la page. Pour que votre paume s'ouvre vers la gauche, là où pointe la force centripète (et donc la force magnétique), vos doigts doivent changer d'orientation jusqu'à ce qu'ils pointent vers la page. Il s'agit de la direction du champ magnétique appliqué.
2. La période pendant laquelle la particule chargée fait le tour d'un cercle est calculée en utilisant la masse, la charge et le champ magnétique donnés dans le problème. Cela s'avère être.\[T = \dfrac{2\pi m}{qB} = \dfrac{2\pi (6.64 \times 10^{-27}kg)}{(3.2 \times 10^{-19}C)(0.050 \, T)} = 2.6 \times 10^{-6}s.\] Cependant, pour le problème donné, la particule alpha fait le tour du quart du cercle, donc le temps que cela prend serait\[t = 0.25 \times 2.61 \times 10^{-6}s = 6.5 \times 10^{-7}s.\]

L'importance

Ce délai peut être assez rapide pour atteindre le matériau que nous aimerions bombarder, selon la courte durée de vie de l'isotope radioactif et continue d'émettre des particules alpha. Si nous pouvions augmenter le champ magnétique appliqué dans la région, le temps serait encore plus court. La trajectoire que doivent emprunter les particules pourrait être raccourcie, mais cela pourrait ne pas être rentable compte tenu de la configuration expérimentale.

Exercice\(\PageIndex{1}\)

Un champ magnétique uniforme de magnitude 1,5 T est dirigé horizontalement d'ouest en est. (a) Quelle est la force magnétique exercée sur un proton au moment où il se déplace verticalement vers le bas dans le champ à une vitesse de\(4 \times 10^7 \, m/s\) ? (b) Comparez cette force avec le poids w d'un proton.

Solution

a.\(9.6 \times 10^{-12}N\) vers le sud ;

b.\(\dfrac{w}{F_m} = 1.7 \times 10^{-15}\)

Exemple\(\PageIndex{2}\): Helical Motion in a Magnetic Field

Un proton entre dans un champ magnétique uniforme de\(1.0 \times 10^{-4}T\) avec une vitesse de\(5 \times 10^5 \, m/s\). Quel angle doit former le champ magnétique par rapport à la vitesse pour que le pas du mouvement hélicoïdal résultant soit égal au rayon de l'hélice ?

Stratégie

Le pas du mouvement est lié à la vitesse parallèle multipliée par la période du mouvement circulaire, tandis que le rayon se rapporte à la composante de vitesse perpendiculaire. Après avoir réglé le rayon et le pas égaux, déterminez l'angle entre le champ magnétique et la vitesse ou\(\theta\).

Solution

La hauteur est donnée par l'équation \ ref {11.8}, la période est donnée par l'équation \ ref {11.6} et le rayon du mouvement circulaire est donné par l'équation \ ref {11.5}. Notez que la vitesse dans l'équation du rayon est liée uniquement à la vitesse perpendiculaire, c'est-à-dire à l'endroit où se produit le mouvement circulaire. Par conséquent, nous substituons la composante sinusoïdale de la vitesse globale dans l'équation du rayon pour égaler le pas et le rayon

\[p = r\]

\[v_{\parallel}T = \dfrac{mv}{qB}\]

\[v \, cos \, \theta \dfrac{2\pi m}{qB} = \dfrac{mv \, sin \, \theta}{qB}\]

\[2\pi = tan \, \theta\]

\[\theta = 81.0^o.\]

L'importance

Si cet angle était le cas\(0^o\), seule une vitesse parallèle se produirait et l'hélice ne se formerait pas, car il n'y aurait aucun mouvement circulaire dans le plan perpendiculaire. Si cet angle était\(90^o\) uniquement le cas, un mouvement circulaire se produirait et il n'y aurait aucun mouvement des cercles perpendiculaires au mouvement. C'est ce qui crée le mouvement hélicoïdal.