11.3 : Champs et lignes magnétiques
- Page ID
- 191240
À la fin de cette section, vous serez en mesure de :
- Définissez le champ magnétique en fonction d'une charge mobile soumise à une force
- Appliquez la règle de la main droite pour déterminer la direction d'une force magnétique en fonction du mouvement d'une charge dans un champ magnétique
- Esquissez des lignes de champ magnétique pour comprendre la direction du champ magnétique et son intensité dans une région de l'espace.
Nous avons décrit les propriétés des aimants, décrit leur comportement et répertorié certaines des applications des propriétés magnétiques. Même s'il n'existe pas de charges magnétiques isolées, nous pouvons tout de même définir l'attraction et la répulsion des aimants comme étant basées sur un champ. Dans cette section, nous définissons le champ magnétique, déterminons sa direction en fonction de la règle de la main droite et expliquons comment tracer des lignes de champ magnétique.
Définition du champ magnétique
Un champ magnétique est défini par la force qu'une particule chargée subit en se déplaçant dans ce champ, après avoir pris en compte les forces gravitationnelles et toutes les forces électriques supplémentaires possibles sur la charge. L'amplitude de cette force est proportionnelle à la quantité de charge q, à la vitesse de la particule chargée v et à l'intensité du champ magnétique appliqué. La direction de cette force est perpendiculaire à la fois à la direction de la particule chargée en mouvement et à la direction du champ magnétique appliqué. Sur la base de ces observations, nous définissons l'intensité du champ magnétique B en fonction de la force magnétique exercée\(\vec{F}\) sur une charge q se déplaçant à vitesse comme le produit croisé de la vitesse et du champ magnétique, c'est-à-dire
\[\vec{F} = q\vec{v} \times \vec{B}. \label{eq1}\]
En fait, c'est ainsi que nous définissons le champ\(\vec{B}\) magnétique, en termes de force exercée sur une particule chargée se déplaçant dans un champ magnétique. L'amplitude de la force est déterminée à partir de la définition du produit croisé en ce qui concerne les magnitudes de chacun des vecteurs. En d'autres termes, l'amplitude de la force satisfait
\[F = qv \, B \sin \, \theta \label{eq2}\]
où θ est l'angle entre la vitesse et le champ magnétique.
L'unité SI pour l'intensité du champ magnétique\(B\) est appelée tesla (T) d'après l'excentrique mais brillant inventeur Nikola Tesla (1856—1943), où
\[1 \, T = \frac{1 \, N}{A \cdot m}.\]
Une unité plus petite, appelée gauss (G), est parfois utilisée, où
\[1 \, G = 10^{-4} \,T\]
Les aimants permanents les plus puissants ont des champs proches de 2 T ; les électroaimants supraconducteurs peuvent atteindre 10 T ou plus. Le champ magnétique de la Terre à sa surface n'est que d'environ\(5 \times 10^{-5}\, T\) ou\(0.5 \,G\).
La direction de la force magnétique\(\vec{F}\) est perpendiculaire au plan formé par\(\vec{v}\) et\(\vec{B}\) tel que déterminé par la règle de droite 1 (ou RHR-1), illustrée sur la figure\(\PageIndex{1}\).
- Orientez votre main droite de manière à ce que vos doigts s'enroulent dans le plan défini par les vecteurs de vitesse et de champ magnétique.
- À l'aide de votre main droite, passez de la vitesse au champ magnétique avec vos doigts en suivant le plus petit angle possible.
- La force magnétique est dirigée vers l'endroit où pointe votre pouce.
- Si la charge était négative, inversez la direction trouvée par ces étapes.
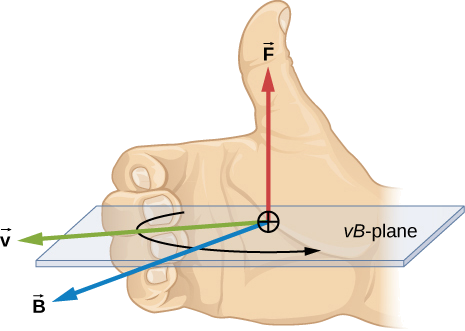
Figure\(\PageIndex{1}\) : Les champs magnétiques exercent des forces sur des charges mobiles. La direction de la force magnétique sur une charge en mouvement est perpendiculaire au plan formé par b\(\vec{v}\)\(\vec{B}\) et suit la règle 1 de la main droite (RHR-1), comme indiqué. L'amplitude de la force est proportionnelle à\(q, \, v, \, B,\) et au sinus de l'angle entre\(\vec{v}\) et\(\vec{B}\).
Visitez ce site Web pour vous entraîner davantage à la direction des champs magnétiques.
Il n'y a aucune force magnétique sur les charges statiques. Cependant, il existe une force magnétique sur les charges se déplaçant à un angle par rapport à un champ magnétique. Lorsque les charges sont stationnaires, leurs champs électriques n'affectent pas les aimants. Cependant, lorsque les charges se déplacent, elles produisent des champs magnétiques qui exercent des forces sur d'autres aimants. Lorsqu'il y a un mouvement relatif, une connexion entre les forces électriques et magnétiques émerge, chacune affectant l'autre.
Une particule alpha\((q = 3.2 \times 10^{-19}C)\) se déplace à travers un champ magnétique uniforme dont l'amplitude est de 1,5 T. Le champ est directement parallèle à l'axe z positif du système de coordonnées rectangulaires de la Figure\(\PageIndex{2}\). Quelle est la force magnétique exercée sur la particule alpha lorsqu'elle se déplace (a) dans la direction x positive à une vitesse de\(5.0 \times 10^4 m/s\) ? (b) dans la direction y négative avec une vitesse de\(5.0 \times 10^4 m/s\) ? (c) dans la direction z positive avec une vitesse de\(5.0 \times 10^4 m/s\) ? (d) avec une certaine vélocité\(\vec{v} = \left(2.0 \hat{i} - 3.0 \hat{j} + 1.0 \hat{k} \right) \times 10^4 m/s\) ?
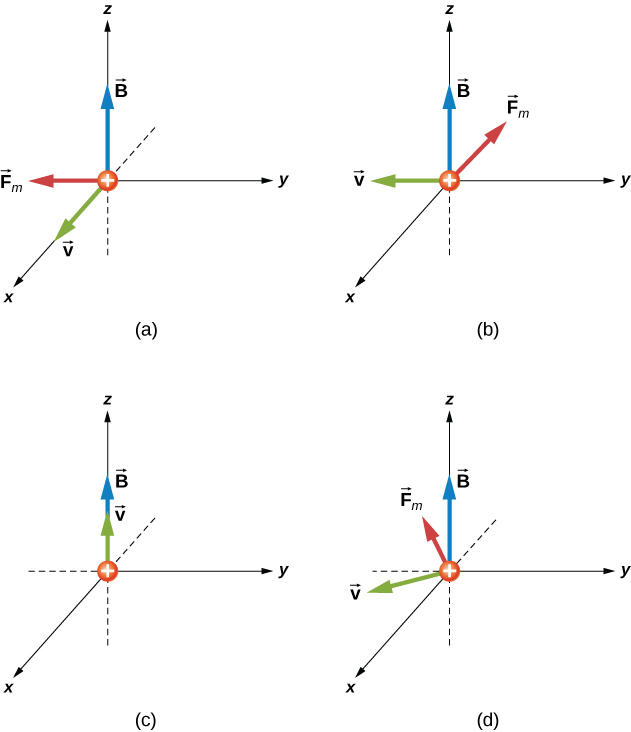
Stratégie
On nous donne la charge, sa vitesse, l'intensité et la direction du champ magnétique. On peut ainsi utiliser l'équation\(\vec{F} = q \vec{v} \times \vec{B}\) ou\(F = qv \, B sin\, \theta\) calculer la force. La direction de la force est déterminée par le RHR-1.
Solution
- Tout d'abord, pour déterminer la direction, commencez par pointer vos doigts dans la direction X positive. Balayez vos doigts vers le haut dans la direction du champ magnétique. Votre pouce doit pointer dans la direction Y négative. Cela doit correspondre à la réponse mathématique. Pour calculer la force, nous utilisons la charge, la vitesse et le champ magnétique donnés, ainsi que la définition de la force magnétique sous forme de produits croisés pour calculer :\[\vec{F} = q\vec{v} \times \vec{B} = (3.2 \times 10^{-19} C) (5.0 \times 10^4 m/s \, \hat{i}) \times (1.5 \, T \, \hat{k}) = - 2.4 \times 10^{-14} N \, \hat{j}\]
- Tout d'abord, pour déterminer la directionnalité, commencez par pointer vos doigts dans la direction Y négative. Balayez vos doigts vers le haut dans la direction du champ magnétique, comme dans le problème précédent. Votre pouce doit être ouvert dans la direction X négative. Cela doit correspondre à la réponse mathématique. Pour calculer la force, nous utilisons la charge, la vitesse et le champ magnétique donnés ainsi que la définition de la force magnétique sous forme de produits croisés pour calculer :\[\vec{F} = q\vec{v} \times \vec{B} = (3.2 \times 10^{-19} C) (- 5.0 \times 10^4 m/s \, \hat{i}) \times (1.5 \, T \, \hat{k}) = - 2.4 \times 10^{-14} N \, \hat{i}\] Une autre approche consiste à utiliser l'équation \ ref {eq2} pour déterminer l'amplitude de la force. Cela s'applique à la fois aux parties (a) et (b). Comme la vitesse est perpendiculaire au champ magnétique, l'angle entre eux est de 90 degrés. Par conséquent, l'ampleur de la force est la suivante :\[F = qv \, B \sin \, \theta = (3.2 \times 10^{-19} C)(5.0 \times 10^4m/s)(1.5 \, T) sin (90^o)) = 2.4 \times 10^{-14} N.\]
- Comme la vitesse et le champ magnétique sont parallèles l'un à l'autre, aucune orientation de votre main ne peut donner lieu à une direction de force. Par conséquent, la force exercée sur cette charge mobile est nulle. Ceci est confirmé par le produit croisé. Lorsque vous croisez deux vecteurs pointant dans la même direction, le résultat est égal à zéro.
- Tout d'abord, pour déterminer la direction, vos doigts peuvent pointer dans n'importe quelle orientation ; cependant, vous devez balayer vos doigts vers le haut dans la direction du champ magnétique. Lorsque vous faites pivoter votre main, remarquez que le pouce peut pointer dans n'importe quelle direction x ou y possible, mais pas dans la direction z. Cela doit correspondre à la réponse mathématique. Pour calculer la force, nous utilisons la charge, la vitesse et le champ magnétique donnés et la définition de la force magnétique sous forme de produits croisés pour calculer :\[\vec{F} = q\vec{v} \times \vec{B} = (3.2 \times 10^{-19} C)((2.0 \hat{i} - 3.0 \hat{j} + 1.0 \hat{k}) \times 10^4 m/s) \times (1.5 \, T \hat{k})\]\[(-14.4 \hat{i} - 9.6 \hat{j}) \times 10^{-15}N.\] Cette solution peut être réécrite en termes de magnitude et d'angle dans le plan xy :\[|\vec{F}| = \sqrt{F_x^2 + F_y^2} = \sqrt{(-14.4)^2 + (-9.6)^2} \times 10^{-15} N = 1.7 \times 10^{-14}N\]\[\theta = tan^{-1} \left(\frac{F_y}{F_x}\right) = tan^{-1} \left(\frac{-9.6 \times 10^{-15}N}{-14.4 \times 10^{-15}N} \right) = 34^o.\] La magnitude de la force peut également être calculée à l'aide de l'équation \ ref {eq2}. La vélocité dans cette question comporte toutefois trois composantes. La composante z de la vitesse peut être négligée, car elle est parallèle au champ magnétique et ne génère donc aucune force. L'amplitude de la vitesse est calculée à partir des composantes x et y. L'angle entre la vitesse dans le plan xy et le champ magnétique dans le plan z est de 90 degrés. Par conséquent, la force est calculée comme suit :\[|\vec{v}| = \sqrt{(2)^2 + (-3)^2} \times 10^4 \frac{m}{s} = 3.6 \times 10^4 \frac{m}{s}\]\[F = qv \, Bsin \, \theta = (3.2 \times 10^{-19}C)(3.6 \times 10^4 m/s) (1.5 \, T) sin (90^o) = 1.7 \times 10^{-14} N\]
L'importance
Le produit croisé de cette formule donne un troisième vecteur qui doit être perpendiculaire aux deux autres. D'autres grandeurs physiques, telles que le moment cinétique, ont également trois vecteurs liés par le produit croisé. Notez que les valeurs de force typiques des problèmes de force magnétique sont beaucoup plus grandes que la force gravitationnelle. Par conséquent, pour une charge isolée, la force magnétique est la force dominante qui régit le mouvement de la charge.
Répétez le problème précédent avec le champ magnétique dans la direction x plutôt que dans la direction z. Vérifiez vos réponses avec RHR-1.
- Répondez à une
-
0 N
- Réponse b
-
\(2.4 \times 10^{-14}\hat{k} N\)
- Réponse c
-
\(2.4 \times 10^{-14}\hat{j} N\)
- Réponse d
-
\(7.2 \hat{j} + 2.2 \hat{k}) \times 10^{-15}N\)
Représentation de champs magnétiques
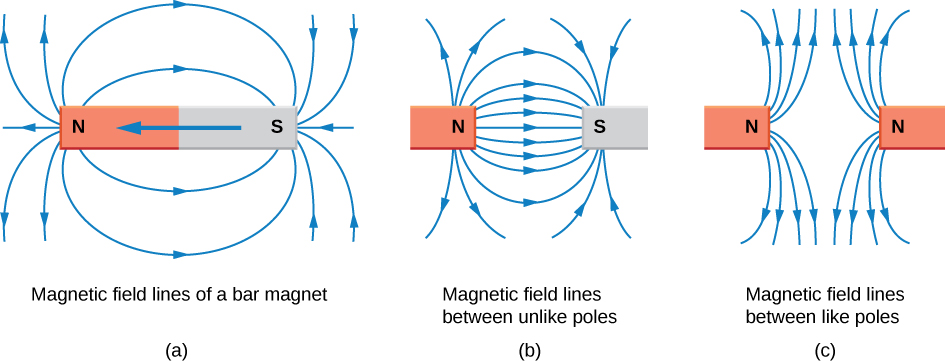
La représentation des champs magnétiques par des lignes de champ magnétique est très utile pour visualiser l'intensité et la direction du champ magnétique. Comme le montre la figure\(\PageIndex{3}\), chacune de ces lignes forme une boucle fermée, même si les contraintes de l'espace disponible pour la figure ne le montrent pas. Les lignes de champ émergent du pôle nord (N), font une boucle jusqu'au pôle sud (S) et continuent à travers le barreau magnétique jusqu'au pôle nord.
Les lignes de champ magnétique sont soumises à plusieurs règles strictes :
- La direction du champ magnétique est tangente à la ligne de champ en tout point de l'espace. Une petite boussole indiquera la direction de la ligne de champ.
- L'intensité du champ est proportionnelle à la proximité des lignes. Elle est exactement proportionnelle au nombre de lignes par unité de surface perpendiculaires aux lignes (appelée densité surfacique).
- Les lignes de champ magnétique ne peuvent jamais se croiser, ce qui signifie que le champ est unique en tout point de l'espace.
- Les lignes de champ magnétique sont continues et forment des boucles fermées sans début ni fin. Ils sont dirigés du pôle nord au pôle sud.
La dernière propriété est liée au fait que les pôles nord et sud ne peuvent pas être séparés. Il s'agit d'une différence marquée par rapport aux lignes de champ électrique, qui commencent généralement sur des charges positives et se terminent sur des charges négatives ou à l'infini. S'il existait des charges magnétiques isolées (appelées monopôles magnétiques), des lignes de champ magnétique commenceraient et se termineraient sur celles-ci.