10.3 : Résistances en série et en parallèle

Objectifs d'apprentissage

À la fin de la section, vous serez en mesure de :

• Définissez le terme résistance équivalente
• Calculez la résistance équivalente des résistances connectées en série
• Calculez la résistance équivalente des résistances connectées en parallèle

Dans Current and Resistance, nous avons décrit le terme « résistance » et expliqué la conception de base d'une résistance. Fondamentalement, une résistance limite le flux de charge dans un circuit et est un dispositif ohmique où\(V = IR\). La plupart des circuits ont plus d'une résistance. Si plusieurs résistances sont connectées ensemble et connectées à une batterie, le courant fourni par la batterie dépend de la résistance équivalente du circuit.

La résistance équivalente d'une combinaison de résistances dépend à la fois de leurs valeurs individuelles et de la manière dont elles sont connectées. Les combinaisons de résistances les plus simples sont les connexions en série et en parallèle (Figure\(\PageIndex{1}\)). Dans un circuit en série, le courant de sortie de la première résistance passe à l'entrée de la seconde résistance ; par conséquent, le courant est le même dans chaque résistance. Dans un circuit parallèle, tous les fils de résistance d'un côté des résistances sont connectés ensemble et tous les fils de l'autre côté sont connectés ensemble. Dans le cas d'une configuration parallèle, chaque résistance présente la même chute de potentiel et les courants à travers chaque résistance peuvent être différents, en fonction de la résistance. La somme des courants individuels est égale au courant qui circule dans les connexions parallèles.

Figure\(\PageIndex{1}\) : (a) Pour une connexion en série de résistances, le courant est le même dans chaque résistance. (b) Pour une connexion en parallèle de résistances, la tension est la même aux bornes de chaque résistance.

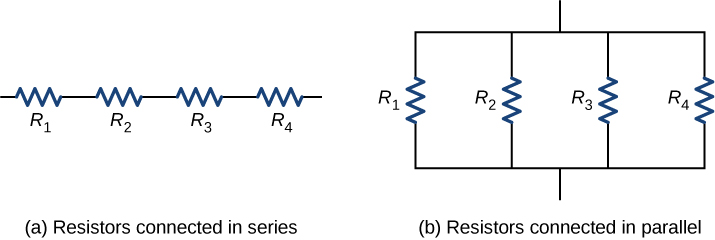
Résistances en série

Les résistances sont dites en série chaque fois que le courant traverse les résistances de manière séquentielle. Considérez la figure\(\PageIndex{2}\), qui montre trois résistances en série avec une tension appliquée égale à\(V_{ab}\). Comme il n'y a qu'un seul chemin pour les charges, le courant est le même dans chaque résistance. La résistance équivalente d'un ensemble de résistances dans une connexion en série est égale à la somme algébrique des résistances individuelles.

Figure\(\PageIndex{2}\) : (a) Trois résistances connectées en série à une source de tension. (b) Le circuit d'origine est réduit à une résistance équivalente et à une source de tension.

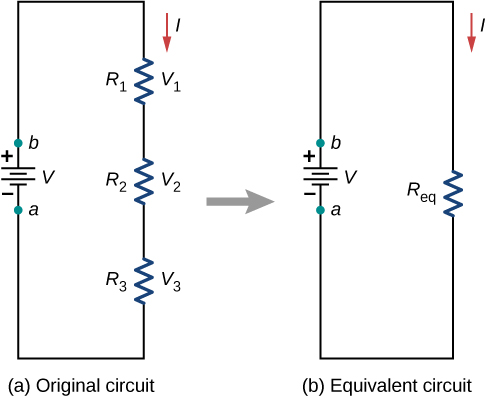
Sur la figure\(\PageIndex{2}\), le courant provenant de la source de tension traverse chaque résistance, de sorte que le courant traversant chaque résistance est le même. Le courant traversant le circuit dépend de la tension fournie par la source de tension et de la résistance des résistances. Pour chaque résistance, il se produit une chute de potentiel égale à la perte d'énergie potentielle électrique lorsqu'un courant traverse chaque résistance. Selon la loi d'Ohm, la chute de potentiel\(V\) à travers une résistance lorsqu'un courant la traverse est calculée à l'aide de l'équation\(V = IR\), où\(I\) est le courant en ampères (\(A\)) et\(R\) la résistance en ohms\((\Omega)\). Puisque l'énergie est conservée et que la tension est égale à l'énergie potentielle par charge, la somme de la tension appliquée au circuit par la source et des chutes de potentiel aux bornes des différentes résistances autour d'une boucle doit être égale à zéro :

\[\sum_{i = 1}^N V_i = 0.\]

Cette équation est souvent appelée loi de la boucle de Kirchhoff, que nous examinerons plus en détail plus loin dans ce chapitre. Pour la figure\(\PageIndex{2}\), la somme de la chute de potentiel de chaque résistance et de la tension fournie par la source de tension doit être égale à zéro :

\[\begin{align*} V - V_1 - V_2 - V_3 &= 0, \\[4pt] V &= V_1 + V_2 + V_3, \\[4pt] &= IR_1 + IR_2 + IR_3, \end{align*}\]

Résoudre pour\(I\)

\[\begin{align*} I &= \frac{V}{R_1 + R_2 + R_3} \\[4pt] &= \frac{V}{R_{S}}. \end{align*}\]

Comme le courant traversant chaque composant est le même, l'égalité peut être simplifiée jusqu'à une résistance équivalente (\(R_{S}\)), qui est juste la somme des résistances des différentes résistances.

Résistance équivalente dans les circuits en série

Un nombre illimité de résistances peuvent être connectées en série. Si\(N\) les résistances sont connectées en série, la résistance équivalente est

\[R_{S} = R_1 + R_2 + R_3 + . . . + R_{N-1} + R_N = \sum_{i=1}^N R_i. \label{equivalent resistance series}\]

L'un des résultats des composants connectés dans un circuit en série est que s'il arrive quelque chose à un composant, cela affecte tous les autres composants. Par exemple, si plusieurs lampes sont connectées en série et qu'une ampoule s'éteint, toutes les autres lampes s'éteignent.

Exemple\(\PageIndex{1}\): Equivalent Resistance, Current, and Power in a Series Circuit

Une batterie dont la tension aux bornes est de 9 V est connectée à un circuit composé de quatre\(20 \, \Omega\) et une\(10 \, \Omega\) résistances toutes en série (Figure\(\PageIndex{3}\)). Supposons que la résistance interne de la batterie soit négligeable.

1. Calculez la résistance équivalente du circuit.
2. Calculez le courant traversant chaque résistance.
3. Calculez la chute de potentiel sur chaque résistance.
4. Déterminez la puissance totale dissipée par les résistances et la puissance fournie par la batterie.

Figure\(\PageIndex{3}\) : Un circuit en série simple avec cinq résistances.

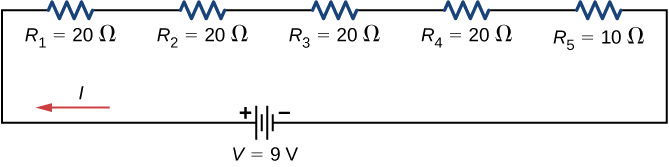
Stratégie

Dans un circuit en série, la résistance équivalente est la somme algébrique des résistances. Le courant traversant le circuit peut être déterminé à partir de la loi d'Ohm et est égal à la tension divisée par la résistance équivalente. La chute de potentiel à travers chaque résistance peut être déterminée en utilisant la loi d'Ohm. La puissance dissipée par chaque résistance peut être trouvée en utilisant\(P = I^2R\), et la puissance totale dissipée par les résistances est égale à la somme de la puissance dissipée par chaque résistance. L'alimentation fournie par la batterie peut être trouvée à l'aide de\(P = I\epsilon\).

Solution

1. La résistance équivalente est la somme algébrique des résistances (équation \ ref {série de résistances équivalentes}) :\[\begin{align*} R_{S} &= R_1 + R_2 + R_3 + R_4 + R_5 \\[4pt] &= 20 \, \Omega + 20 \, \Omega + 20 \, \Omega + 20 \, \Omega + 10 \, \Omega = 90 \, \Omega. \end{align*}\]
2. Le courant traversant le circuit est le même pour chaque résistance d'un circuit en série et est égal à la tension appliquée divisée par la résistance équivalente :\[I = \frac{V}{R_{S}} = \frac{9 \, V}{90 \, \Omega} = 0.1 \, A. \nonumber\] Notez que la somme des chutes de potentiel aux bornes de chaque résistance est égale à la tension fournie par la batterie.
3. La puissance dissipée par une résistance est égale à\(P = I^2R\), et la puissance fournie par la batterie est égale à\(P = I\epsilon\). \[P_1 = P_2 = P_3 = P_4 = (0.1 \, A)^2 (20 \, \Omega) = 0.2 \, W,\nonumber\]\[P_5 = (0.1 \, A)^2 (10 \, \Omega) = 0.1 \, W,\nonumber\]\[P_{dissipated} = 0.2 \, W + 0.2 \, W + 0.2 \, W + 0.2 \, W + 0.1 \, W = 0.9 \, W,\nonumber\]\[P_{source} = I\epsilon = (0.1 \, A)(9 \, V) = 0.9 \, W. \nonumber\]

L'importance

Il y a plusieurs raisons pour lesquelles nous utiliserions plusieurs résistances au lieu d'une seule résistance avec une résistance égale à la résistance équivalente du circuit. Peut-être qu'une résistance de la taille requise n'est pas disponible, que nous devons dissiper la chaleur générée ou que nous voulons minimiser le coût des résistances. Chaque résistance peut coûter de quelques centimes à quelques dollars, mais lorsqu'elle est multipliée par des milliers d'unités, l'économie peut être appréciable.

Exercice\(\PageIndex{1}\)

Certaines guirlandes de lampes de Noël miniatures sont conçues pour court-circuiter lorsqu'une ampoule s'éteint. Le dispositif qui provoque le court-circuit s'appelle un shunt, qui permet au courant de circuler dans le circuit ouvert. Un « short » revient à placer un bout de fil sur le composant. Les ampoules sont généralement regroupées en séries de neuf ampoules. Si trop d'ampoules brûlent, les shunts finissent par s'ouvrir. Quelle en est la cause ?

Réponse

La résistance équivalente de neuf ampoules connectées en série est de 9 R. Le courant est\(I = V/9 \, R\). Si une ampoule s'éteint, la résistance équivalente est de 8 R et la tension ne change pas, mais le courant augmente\((I = V/8 \, R\). À mesure que de plus en plus d'ampoules s'éteignent, le courant augmente encore. Finalement, le courant devient trop élevé, ce qui fait brûler le shunt.

Résumons brièvement les principales caractéristiques des résistances en série :

1. Les résistances des séries s'additionnent pour obtenir la résistance équivalente (équation \ ref {série de résistances équivalentes}) :\[R_{S} = R_1 + R_2 + R_3 + . . . + R_{N-1} + R_N = \sum_{i=1}^N R_i.\]
2. Le même courant traverse chaque résistance en série.
3. Les résistances individuelles en série n'obtiennent pas la tension totale de la source, mais la divisent. La chute de potentiel totale sur une configuration en série de résistances est égale à la somme des chutes de potentiel sur chaque résistance.

Résistances en parallèle

La figure\(\PageIndex{4}\) montre des résistances en parallèle, connectées à une source de tension. Les résistances sont en parallèle lorsqu'une extrémité de toutes les résistances est connectée par un fil continu de résistance négligeable et que l'autre extrémité de toutes les résistances est également connectée l'une à l'autre par un fil continu de résistance négligeable. La chute de potentiel sur chaque résistance est la même. Le courant traversant chaque résistance peut être trouvé en utilisant la loi d'Ohm\(I = V/R\), où la tension est constante aux bornes de chaque résistance. Par exemple, les phares, la radio et les autres systèmes d'une automobile sont câblés en parallèle, de sorte que chaque sous-système utilise la pleine tension de la source et puisse fonctionner de manière totalement indépendante. Il en va de même pour le câblage de votre maison ou de tout bâtiment.

Figure\(\PageIndex{4}\) : Deux résistances connectées en parallèle à une source de tension. (b) Le circuit d'origine est réduit à une résistance équivalente et à une source de tension.

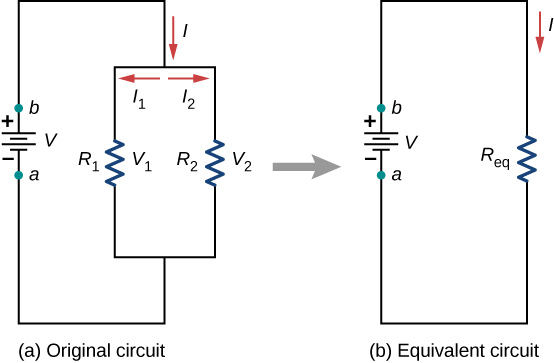
Le courant provenant de la source de tension de la figure\(\PageIndex{4}\) dépend de la tension fournie par la source de tension et de la résistance équivalente du circuit. Dans ce cas, le courant circule depuis la source de tension et entre dans une jonction, ou nœud, où le circuit se divise en passant par des résistances\(R_1\) et\(R_2\). Lorsque les charges proviennent de la batterie, certaines traversent la résistance\(R_1\) et d'autres traversent la résistance\(R_2\). La somme des courants passant dans une jonction doit être égale à la somme des courants sortant de la jonction :

\[\sum I_{in} = \sum I_{out}. \nonumber\]

Cette équation est appelée règle de jonction de Kirchhoff et sera abordée en détail dans la section suivante. Dans la figure\(\PageIndex{4}\), la règle de jonction donne\(I = I_1 + I_2\). Il y a deux boucles dans ce circuit, ce qui conduit aux équations\(V = I_1R_1\) et\(I_1R_1 = I_2R_2\). Notez que la tension aux bornes des résistances en parallèle est la même (\(V = V_1 = V_2\)) et que le courant est additif :

\[ \begin{align*}  I &= I_1 + I_2 \\[4pt] &= \frac{V_1}{R_1} + \frac{V_2}{R_2} \\[4pt] &= \frac{V}{R_1} + \frac{V}{R_2} \\[4pt] &= V \left( \frac{1}{R_1} + \frac{1}{R_2} \right) = \frac{V}{R_{P}}\end{align*}\]

Résoudre pour\(R_{P}\)

\[R_{P} = \left(\frac{1}{R_1} + \frac{1}{R_2} \right)^{-1}. \]

Résistance équivalente dans les circuits parallèles

En généralisant à n'importe quel nombre de\(N\) résistances, la résistance équivalente\(R_{P}\) d'une connexion parallèle est liée aux résistances individuelles par

\[R_{P} = \left( \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + . . . + \frac{1}{R_{N-1}} + \frac{1}{R_N} \right)^{-1} = \left(\sum_{i=1}^N \frac{1}{R_i} \right)^{-1}. \label{10.3}\]

Cette relation se traduit par une résistance équivalente\(R_{P}\) qui est inférieure à la plus petite des résistances individuelles. Lorsque les résistances sont connectées en parallèle, plus de courant circule depuis la source que ce n'est le cas pour chacune d'entre elles individuellement, de sorte que la résistance totale est plus faible.

Exemple\(\PageIndex{2}\): Analysis of a parallel circuit

Trois résistances\(R_1 = 1.00 \, \Omega\)\(R_2 = 2.00 \, \Omega\), et\(R_3 = 2.00 \, \Omega\), sont connectées en parallèle. La connexion parallèle est raccordée à une source\(V = 3.00 \, V\) de tension.

1. Quelle est la résistance équivalente ?
2. Trouvez le courant fourni par la source au circuit parallèle.
3. Calculez les courants dans chaque résistance et montrez qu'ils s'additionnent pour égaliser le courant de sortie de la source.
4. Calculez la puissance dissipée par chaque résistance.
5. Trouvez la puissance de sortie de la source et montrez qu'elle est égale à la puissance totale dissipée par les résistances.

Stratégie

(a) La résistance totale pour une combinaison parallèle de résistances est déterminée à l'aide de l'équation \ ref {10.3}. (Notez que dans ces calculs, chaque réponse intermédiaire est indiquée par un chiffre supplémentaire.)

(b) Le courant fourni par la source peut être déterminé à partir de la loi d'Ohm, en\(R_{P}\) substituant la résistance totale\(I = \frac{V}{R_{P}}\).

(c) Les courants individuels sont facilement calculés à partir de la loi d'Ohm\(\left(I_i = \frac{V_i}{R_i}\right)\), puisque chaque résistance reçoit la pleine tension. Le courant total est la somme des courants individuels :\[I = \sum_i I_i. \nonumber\]

(d) La puissance dissipée par chaque résistance peut être déterminée à l'aide de l'une des équations reliant la puissance au courant, à la tension et à la résistance, puisque les trois sont connues. Utilisons-le\(P_i = V^2 /R_i\), car chaque résistance est à pleine tension.

(e) La puissance totale peut également être calculée de plusieurs manières, utilisez\(P = IV\).

Solution

1. La résistance totale pour une combinaison parallèle de résistances est déterminée à l'aide de l'équation \ ref {10.3}. La saisie de valeurs connues donne\[R_{P} = \left( \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} \right)^{-1} = \left(\frac{1}{1.00 \, \Omega} + \frac{1}{2.00 \, \Omega} + \frac{1}{2.00 \, \Omega} \right)^{-1} = 0.50 \, \Omega.\nonumber\] La résistance totale avec le nombre correct de chiffres significatifs est\(R_{eq} = 0.50 \, \Omega\). Comme prévu,\(R_{P}\) est inférieur à la plus petite résistance individuelle.
2. Le courant total peut être déterminé à partir de la loi d'Ohm, en remplacement\(R_{P}\) de la résistance totale. Cela donne que le\[I = \frac{V}{R_{P}} = \frac{3.00 \, V}{0.50 \, \Omega} = 6.00 \, A.\nonumber\] courant I pour chaque appareil est beaucoup plus grand que pour les mêmes appareils connectés en série (voir l'exemple précédent). Un circuit avec des connexions en parallèle possède une résistance totale inférieure à celle des résistances connectées en série.
3. Les courants individuels sont facilement calculés à partir de la loi d'Ohm, car chaque résistance reçoit la pleine tension. Ainsi, de\[I_1 = \frac{V}{R_1} = \frac{3.00 \, V}{1.00 \, \Omega} = 3.00 \, A.\nonumber\] même,\[I_2 = \frac{V}{R_2} = \frac{3.00 \, V}{2.00 \, \Omega} = 1.50 \, A\nonumber\] et\[I_3 = \frac{V}{R_3} = \frac{3.00 \, V}{2.00 \, \Omega} = 1.50 \, A.\nonumber\] le courant total est la somme des courants individuels :\[I_1 + I_2 + I_3 = 6.00 \, A.\nonumber\]
4. La puissance dissipée par chaque résistance peut être déterminée à l'aide de l'une des équations reliant la puissance au courant, à la tension et à la résistance, puisque les trois sont connues. Utilisons-le\(P = V^2 /R\), car chaque résistance est à pleine tension. Ainsi, de\[P_1 = \frac{V^2}{R_1} = \frac{(3.00 \, V)^2}{1.00 \, \Omega} = 9.00 \, W.\nonumber\] même,\[P_2 = \frac{V^2}{R_2} = \frac{(3.00 \, V)^2}{2.00 \, \Omega} = 4.50 \, W.\nonumber\] et\[P_3 = \frac{V^2}{R_3} = \frac{(3.00 \, V)^2}{2.00 \, \Omega} = 4.50 \, W.\nonumber\]
5. La puissance totale peut également être calculée de plusieurs manières. Choix\(P = IV\) et saisie des rendements courants totaux\[P = IV = (6.00 \, A)(3.00 \, V) = 18.00 \, W.\nonumber\]

L'importance

La puissance totale dissipée par les résistances est également de 18,00 W :

\[P_1 + P_2 + P_3 = 9.00 \, W + 4.50 \, W + 4.50 \, W = 18.00 \, W.\nonumber\]

Notez que la puissance totale dissipée par les résistances est égale à la puissance fournie par la source.

Exercice\(\PageIndex{2A}\)

Considérez la même différence de potentiel\((V = 3.00 \, V)\) appliquée aux trois mêmes résistances connectées en série. La résistance équivalente du circuit série serait-elle supérieure, inférieure ou égale aux trois résistances en parallèle ? Le courant traversant le circuit en série serait-il supérieur, inférieur ou égal au courant fourni par la même tension appliquée au circuit parallèle ? Comment la puissance dissipée par la résistance en série serait-elle comparée à la puissance dissipée par les résistances en parallèle ?

Solution

L'équivalent du circuit en série serait\(R_{eq} = 1.00 \, \Omega + 2.00 \, \Omega + 2.00 \, \Omega = 5.00 \, \Omega\), ce qui est supérieur à la résistance équivalente du circuit parallèle\(R_{eq} = 0.50 \, \Omega\). La résistance équivalente d'un nombre quelconque de résistances est toujours supérieure à la résistance équivalente des mêmes résistances connectées en parallèle. Le courant traversant le circuit série serait de\(I = \frac{3.00 \, V}{5.00 \, \Omega} = 0.60 \, A\), qui est inférieur à la somme des courants traversant chaque résistance du circuit parallèle,\(I = 6.00 \, A\). Cela n'est pas surprenant car la résistance équivalente du circuit série est plus élevée. Le courant traversant une connexion en série d'un nombre quelconque de résistances sera toujours inférieur au courant passant dans une connexion parallèle des mêmes résistances, car la résistance équivalente du circuit série sera supérieure à celle du circuit parallèle. La puissance dissipée par les résistances en série serait de\(P = 1.800 \, W\), ce qui est inférieur à la puissance dissipée dans le circuit parallèle\(P = 18.00 \, W\).

Exercice\(\PageIndex{2B}\)

Comment utiliseriez-vous une rivière et deux cascades pour modéliser une configuration parallèle de deux résistances ? Comment se décompose cette analogie ?

Solution

Une rivière, qui coule horizontalement à un débit constant, se divise en deux et coule au-dessus de deux cascades. Les molécules d'eau sont analogues aux électrons des circuits parallèles. Le nombre de molécules d'eau qui circulent dans la rivière et les chutes doit être égal au nombre de molécules qui circulent au-dessus de chaque cascade, tout comme la somme du courant traversant chaque résistance doit être égale au courant circulant dans le circuit parallèle. Les molécules d'eau de la rivière ont de l'énergie en raison de leur mouvement et de leur hauteur. L'énergie potentielle des molécules d'eau de la rivière est constante en raison de leur hauteur égale. Ceci est analogue à la variation constante de la tension dans un circuit parallèle. La tension est l'énergie potentielle aux bornes de chaque résistance.

L'analogie se décompose rapidement lorsqu'on considère l'énergie. Dans la cascade, l'énergie potentielle est convertie en énergie cinétique des molécules d'eau. Dans le cas d'électrons traversant une résistance, la chute de potentiel est convertie en chaleur et en lumière, et non en énergie cinétique des électrons.

Résumons les principales caractéristiques des résistances en parallèle :

1. La résistance équivalente est déterminée à partir de l'équation \ ref {10.3} et est inférieure à toute résistance individuelle de la combinaison.
2. La chute de potentiel sur chaque résistance en parallèle est la même.
3. Les résistances parallèles ne reçoivent pas toutes le courant total ; elles le divisent. Le courant entrant dans une combinaison parallèle de résistances est égal à la somme du courant traversant chaque résistance en parallèle.

Dans ce chapitre, nous avons introduit la résistance équivalente des résistances connectées en série et des résistances connectées en parallèle. Vous vous souvenez peut-être que dans la section sur la capacité, nous avons introduit la capacité équivalente des condensateurs connectés en série et en parallèle. Les circuits contiennent souvent à la fois des condensateurs et des résistances. \(\PageIndex{1}\)Le tableau résume les équations utilisées pour la résistance équivalente et la capacité équivalente pour les connexions en série et en parallèle.

Tableau\(\PageIndex{1}\) : Résumé de la résistance et de la capacité équivalentes dans les combinaisons en série et en parallèle

	Combinaison de séries	Combinaison parallèle
Capacité équivalente	\[\frac{1}{C_{S} }= \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3} + . . . \nonumber\]	\[C_{P} = C_1 + C_2 + C_3 + . . . \nonumber\]
Résistance équivalente	\[R_{S} = R_1 + R_2 + R_3 + . . . = \sum_{i=1}^N R_i \nonumber\]	\[\frac{1}{R_{P}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + . . . \nonumber\]

Combinaisons de séries et de parallèles

Les connexions plus complexes de résistances ne sont souvent que des combinaisons de connexions en série et en parallèle. De telles combinaisons sont courantes, en particulier lorsque la résistance des fils est prise en compte. Dans ce cas, la résistance du fil est en série avec d'autres résistances qui sont en parallèle.

Les combinaisons de série et de parallèle peuvent être réduites à une seule résistance équivalente en utilisant la technique illustrée à la figure\(\PageIndex{5}\). Les différentes pièces peuvent être identifiées comme des connexions en série ou en parallèle, réduites à leurs résistances équivalentes, puis réduites jusqu'à ce qu'il ne reste qu'une seule résistance équivalente. Le processus est plus long que difficile. Ici, nous notons la résistance équivalente à\(R_{eq}\).

Figure\(\PageIndex{5}\) : (a) Le circuit original de quatre résistances. (b) Étape 1 : Les résistances\(R_3\) et\(R_4\) sont en série et la résistance équivalente est\(R_{34} = 10 \, \Omega\) (c) Étape 2 : Le circuit réduit montre les résistances\(R_2\) et\(R_{34}\) sont en parallèle, avec une résistance équivalente de\(R_{234} = 5 \, \Omega\). (d) Étape 3 : Le circuit réduit indique que\(R_1\) et\(R_{234}\) sont en série avec une résistance équivalente\(R_{1234} = 12 \, \Omega\) dont la résistance est équivalente\(R_{eq}\). (e) Le circuit réduit avec une source de tension ou\(V = 24 \, V\) avec une résistance équivalente de\(R_{eq} = 12 \, \Omega\). Il en résulte un courant de\(I = 2 \, A\) provenant de la source de tension.

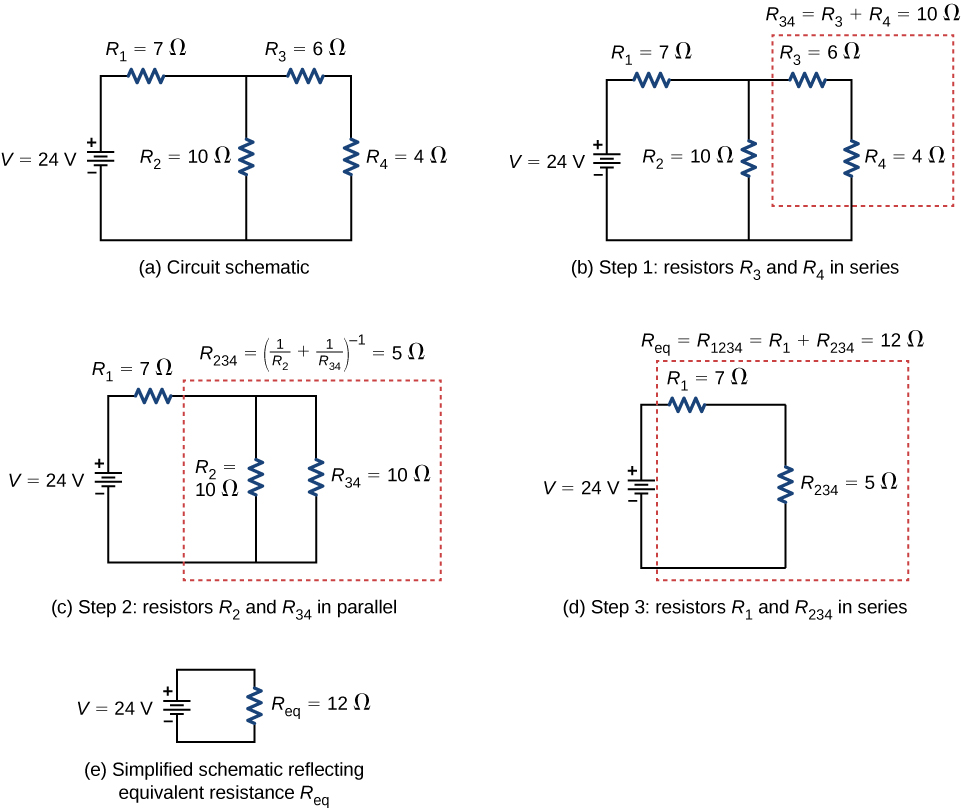
Notez que les résistances\(R_3\) et\(R_4\) sont en série. Ils peuvent être combinés en une seule résistance équivalente. Une méthode pour suivre le processus consiste à inclure les résistances sous forme d'indices. Ici, la résistance équivalente de\(R_3\) et\(R_4\) est

\[R_{34} = R_3 + R_4 = 6 \, \Omega + 4 \, \Omega = 10 \, \Omega. \nonumber\]

Le circuit est maintenant réduit à trois résistances, comme indiqué sur la figure\(\PageIndex{5c}\). En redessinant, nous voyons maintenant que les résistances\(R_2\) et\(R_{34}\) constituent un circuit parallèle. Ces deux résistances peuvent être réduites à une résistance équivalente :

\[R_{234} = \left( \frac{1}{R_2} + \frac{1}{R_{34}}\right)^{-1} = \left(\frac{1}{10 \, \Omega} + \frac{1}{10 \, \Omega} \right)^{-1} = 5 \, \Omega. \nonumber\]

Cette étape du processus réduit le circuit à deux résistances, comme le montre la figure\(\PageIndex{5d}\). Ici, le circuit se réduit à deux résistances, qui dans ce cas sont en série. Ces deux résistances peuvent être réduites à une résistance équivalente, qui est la résistance équivalente du circuit :

\[R_{eq} = R_{1234} = R_1 + R_{234} = 7 \, \Omega + 5 \Omega = 12 \, \Omega. \nonumber\]

L'objectif principal de cette analyse du circuit est atteint et le circuit est maintenant réduit à une seule résistance et à une seule source de tension.

Nous pouvons maintenant analyser le circuit. Le courant fourni par la source de tension est de\(I = \frac{V}{R_{eq}} = \frac{24 \, V}{12 \, \Omega} = 2 \, A\). Ce courant traverse la résistance\(R_1\) et est désigné comme\(I_1\). La chute potentielle\(R_1\) peut être déterminée en utilisant la loi d'Ohm :

\[V_1 = I_1R_1 = (2 \, A)(7 \, \Omega) = 14 \, V. \nonumber\]

En regardant la figure\(\PageIndex{5c}\), cela laisse\(24 \, V - 14 \, V = 10 \, V\) tomber la combinaison parallèle de\(R_2\) et\(R_{34}\). Le courant traversant\(R_2\) peut être trouvé en utilisant la loi d'Ohm :

\[I_2 = \frac{V_2}{R_2} = \frac{10 \, V}{10 \, \Omega} = 1 \, A. \nonumber\]

Les résistances\(R_3\) et\(R_4\) les résistances sont en série, donc les courants\(I_3\) et\(I_4\) sont égaux à

\[I_3 = I_4 = I - I_2 = 2 \, A - 1 \, A = 1 \, A. \nonumber\]

En utilisant la loi d'Ohm, nous pouvons déterminer la chute de potentiel entre les deux dernières résistances. Les baisses potentielles sont\(V_3 = I_3R_3 = 6 \, V\) et\(V_4 = I_4R_4 = 4 \, V\). L'analyse finale consiste à examiner la puissance fournie par la source de tension et la puissance dissipée par les résistances. La puissance dissipée par les résistances est

\[\begin{align*}P_1 &= I_1^2R_1 = (2 \, A)^2 (7 \, \Omega) = 28 \, W, \\[4pt] P_2 &= I_2^2R_2 = (1 \, A)^2 (10 \, \Omega) = 10 \, W, \\[4pt] P_3 &= I_3^2R_3 = (1 \, A)^2 (6 \, \Omega) = 6 \, W, \\[4pt] P_4 &= I_4^2R_4 = (1 \, A)^2 (4 \, \Omega) = 4 \, W, \\[4pt] P_{dissipated} &= P_1 + P_2 + P_3 + P_4 = 48 \, W. \end{align*}\]

L'énergie totale est constante dans n'importe quel processus. Par conséquent, la puissance fournie par la source de tension est

\[\begin{align*} P_s &= IV \\[4pt] &= (2 \, A)(24 \, V) = 48 \, W \end{align*}\]

L'analyse de la puissance fournie au circuit et de la puissance dissipée par les résistances permet de vérifier la validité de l'analyse ; elles doivent être égales.

Exemple\(\PageIndex{3}\): Combining Series and parallel circuits

La figure\(\PageIndex{6}\) montre des résistances câblées en série et en parallèle. On peut\(R_1\) considérer comme la résistance des fils menant à\(R_2\) et\(R_3\).

1. Déterminez la résistance équivalente du circuit.
2. Quelle est la chute de potentiel aux bornes\(V_1\) de la résistance\(R_1\) ?
3. Trouvez le courant\(I_2\) traversant la résistance\(R_2\).
4. Par quel pouvoir se dissipe\(R_2\) ?

Figure\(\PageIndex{6}\) : Ces trois résistances sont connectées à une source de tension de telle sorte qu'\(R_2\)\(R_3\)elles soient en parallèle les unes avec les autres et que cette combinaison soit en série avec\(R_1\).

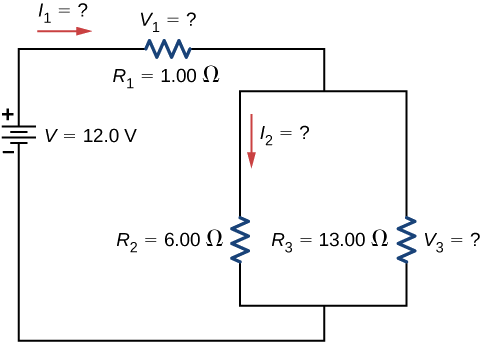
Stratégie

(a) Pour trouver la résistance équivalente, trouvez d'abord la résistance équivalente de la connexion parallèle de\(R_2\) et\(R_3\). Utilisez ensuite ce résultat pour trouver la résistance équivalente de la connexion en série avec\(R_1\).

(b) Le courant traversant\(R_1\) peut être déterminé en utilisant la loi d'Ohm et la tension appliquée. Le courant traversant\(R_1\) est égal au courant provenant de la batterie. La chute de potentiel aux\(V_1\) bornes de la résistance\(R_1\) (qui représente la résistance dans les fils de connexion) peut être déterminée en utilisant la loi d'Ohm.

(c) Le courant traversant\(R_2\) peut être déterminé en utilisant la loi d'Ohm\(I_2 = \frac{V_2}{R_2}\). La tension aux bornes\(R_2\) peut être trouvée en utilisant\(V_2 = V - V_1\).

(d) En utilisant la loi d'Ohm\((V_2 = I_2R_2)\), la puissance dissipée par la résistance peut également être trouvée en utilisant\(P_2 = I_2^2 R_2 = \frac{V_2^2}{R_2}\).

Solution

1. Pour trouver la résistance équivalente du circuit, notez que la connexion en parallèle de\(R_2\) et\(R_3\) est en série avec\(R_1\), donc la résistance équivalente est.\[R_{eq} = R_1 + \left(\frac{1}{R_2} + \frac{1}{R_3} \right)^{-1} = 1.00 \, \Omega + \left(\frac{1}{6.00 \, \Omega} + \frac{1}{13.00 \, \Omega}\right)^{-1} = 5.10 \, \Omega.\nonumber\] La résistance totale de cette combinaison est intermédiaire entre les valeurs de série pure et de parallèle pur (\(20.0 \, \Omega\)et \(0.804 \, \Omega\), respectivement).
2. Le courant traversant\(R_1\) est égal au courant fourni par la batterie :\[I_1 = I = \frac{V}{R_{eq}} = \frac{12.0 \, V}{5.10 \, \Omega} = 2.35 \, A.\nonumber\] La tension aux bornes\(R_1\) est\[V_1 = I_1R_1 = (2.35 \, A)(1 \, \Omega) = 2.35 \, V.\nonumber\] la tension appliquée\(R_2\) et\(R_3\) est inférieure à la tension fournie par la batterie d'une certaine quantité\(V_1\). Lorsque la résistance du fil est importante, elle peut affecter de manière significative le fonctionnement des dispositifs représentés par\(R_2\) et\(R_3\).
3. Pour connaître le courant qui le traverse\(R_2\), il faut d'abord trouver la tension qui lui est appliquée. La tension aux bornes des deux résistances en parallèle est la même : nous pouvons\[V_2 = V_3 = V - V_1 = 12.0 \, V - 2.35 \, V = 9.65 \, V.\nonumber\] maintenant trouver le courant\(I_2\) traversant la résistance\(R_2\) en utilisant la loi d'Ohm :\[I_2 = \frac{V_2}{R_2} = \frac{9.65 \, V}{6.00 \, \Omega} = 1.61 \, A.\nonumber\] le courant est inférieur aux 2,00 A qui circulaient\(R_2\) lorsqu'il était connecté en parallèle à la batterie dans la précédente exemple de circuit parallèle.
4. La puissance dissipée par\(R_2\) est donnée par\[P_2 = I_2^2R_2 = (1.61 \, A)^2 (6.00 \, \Omega) = 15.5 \, W. \nonumber\]

L'importance

L'analyse de circuits complexes peut souvent être simplifiée en réduisant le circuit à une source de tension et à une résistance équivalente. Même si l'ensemble du circuit ne peut pas être réduit à une seule source de tension et à une seule résistance équivalente, certaines parties du circuit peuvent être réduites, simplifiant considérablement l'analyse.

Exercice\(\PageIndex{3}\)

Tenez compte des circuits électriques de votre maison. Donnez au moins deux exemples de circuits qui doivent utiliser une combinaison de circuits en série et en parallèle pour fonctionner efficacement.

Solution

Tous les circuits d'éclairage de plafond sont en parallèle et connectés à la ligne d'alimentation principale. Ainsi, lorsqu'une ampoule s'éteint, tous les plafonniers ne s'assombrissent pas. Chaque plafonnier aura au moins un interrupteur en série avec l'éclairage, afin que vous puissiez l'allumer et l'éteindre.

Un réfrigérateur est équipé d'un compresseur et d'une lumière qui s'allume lorsque la porte s'ouvre. Il n'y a généralement qu'un seul cordon à brancher au mur pour le réfrigérateur. Le circuit contenant le compresseur et le circuit contenant le circuit d'éclairage sont en parallèle, mais il y a un interrupteur en série avec la lumière. Un thermostat commande un interrupteur qui se trouve en série avec le compresseur pour contrôler la température du réfrigérateur.

Implications pratiques

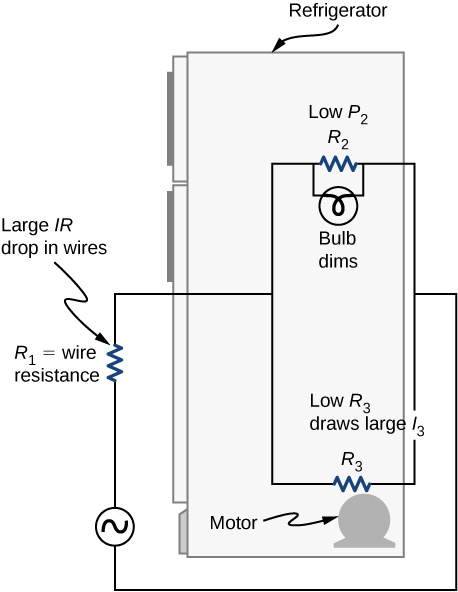
L'une des implications de ce dernier exemple est que la résistance dans les fils réduit le courant et la puissance fournis à une résistance. Si la résistance du fil est relativement importante, comme dans le cas d'une rallonge usée (ou très longue), cette perte peut être importante. Si un courant important est consommé, la chute infrarouge dans les fils peut également être importante et peut se manifester par la chaleur générée dans le cordon.

Par exemple, lorsque vous fouillez dans le réfrigérateur et que le moteur s'allume, le voyant du réfrigérateur s'éteint momentanément. De même, vous pouvez voir la lumière de l'habitacle s'atténuer lorsque vous démarrez le moteur de votre voiture (bien que cela puisse être dû à la résistance à l'intérieur de la batterie elle-même).

Ce qui se passe dans ces situations de forte intensité est illustré dans la figure\(\PageIndex{7}\). L'appareil représenté par\(R_3\) a une très faible résistance, donc lorsqu'il est allumé, un courant important circule. Cette augmentation du courant provoque une chute infrarouge plus importante dans les fils représentés par\(R_1\), réduisant ainsi la tension aux bornes de l'ampoule (qui est\(R_2\)), qui diminue alors sensiblement.

Figure\(\PageIndex{7}\) : Pourquoi les lumières faiblissent-elles lorsqu'un gros appareil est allumé ? La réponse est que le courant important consommé par le moteur de l'appareil provoque une chute infrarouge significative dans les fils et réduit la tension aux bornes de l'éclairage.

Stratégie de résolution de problèmes : résistances en série et en parallèle

1. Dessinez un schéma de circuit clair, en étiquetant toutes les résistances et les sources de tension. Cette étape inclut une liste des valeurs connues du problème, car elles sont étiquetées dans votre schéma de circuit.
2. Identifiez exactement ce qui doit être déterminé dans le problème (identifiez les inconnues). Une liste écrite est utile.
3. Déterminez si les résistances sont en série, en parallèle ou une combinaison des deux. Examinez le schéma du circuit pour effectuer cette évaluation. Les résistances sont en série si le même courant doit les traverser séquentiellement.
4. Utilisez la liste appropriée des principales fonctionnalités pour les connexions en série ou en parallèle afin de résoudre les inconnues. Il existe une liste pour les séries et une autre pour les séries parallèles.
5. Vérifiez si les réponses sont raisonnables et cohérentes.

Exemple\(\PageIndex{4}\): Combining Series and Parallel circuits

Deux résistances connectées en série\((R_1, \, R_2)\) sont connectées à deux résistances connectées en parallèle\((R_3, \, R_4)\). La combinaison série-parallèle est connectée à une batterie. Chaque résistance a une résistance de 10,00 ohms. Les fils reliant les résistances et la batterie ont une résistance négligeable. Un courant de 2,00 ampères traverse la résistance\(R_1\). Quelle est la tension fournie par la source de tension ?

Stratégie

Suivez les étapes de la stratégie de résolution de problèmes précédente pour trouver la solution à cet exemple.

Solution

Figure\(\PageIndex{8}\) : Pour trouver la tension inconnue, il faut d'abord trouver la résistance équivalente du circuit.

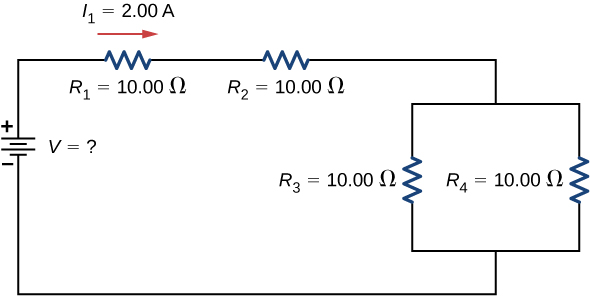
1. Dessinez un schéma de circuit clair (Figure\(\PageIndex{8}\)).
2. L'inconnu est la tension de la batterie. Pour trouver la tension fournie par la batterie, il faut trouver la résistance équivalente.
3. Dans ce circuit, nous savons déjà que les résistances\(R_1\) et\(R_2\) sont en série et que les résistances\(R_3\) et\(R_4\) sont en parallèle. La résistance équivalente de la configuration parallèle des résistances\(R_4\) est\(R_3\) en série avec la configuration en série des résistances\(R_1\) et\(R_2\).
4. La tension fournie par la batterie peut être déterminée en multipliant le courant de la batterie et la résistance équivalente du circuit. Le courant de la batterie est égal au courant traversant\(R_1\) et est égal à 2,00 A. Nous devons trouver la résistance équivalente en réduisant le circuit. Pour réduire le circuit, considérez d'abord les deux résistances en parallèle. La résistance équivalente est\[R_{34} = \left(\frac{1}{10.00 \, \Omega} + \frac{1}{10.00 \, \Omega}\right)^{-1} = 5.00 \, \Omega. \nonumber\] Cette combinaison parallèle est en série avec les deux autres résistances, donc la résistance équivalente du circuit est\(R_{eq} = R_1 + R_2 + R_{34} = (25.00 \, \Omega\). La tension fournie par la batterie est donc de\(V = IR_{eq} = 2.00 \, A (25.00 \, \Omega) = 50.00 \, V\).
5. Une façon de vérifier la cohérence de vos résultats consiste à calculer la puissance fournie par la batterie et la puissance dissipée par les résistances. L'alimentation fournie par la batterie est de\(P_{batt} = IV = 100.00 \, W\).

Comme ils sont en série, le courant traversant\(R_2\) est égal au courant traversant\(R_1\). Depuis\(R_3 = R_4\), le courant traversant chacun sera de 1,00 ampères. La puissance dissipée par les résistances est égale à la somme de la puissance dissipée par chaque résistance :

\[\begin{align*} P &= I_1^2R_1 + I_2^2R_2 + I_3^2R_3 + I_4^2R_4 \\[4pt] &= 40.00 \, W + 40.00 \, W + 10.00 \, W + 10.00 \, W = 100. \, W. \end{align*}\]

Puisque la puissance dissipée par les résistances est égale à la puissance fournie par la batterie, notre solution semble cohérente.

L'importance

Si un problème comporte une combinaison de séries et de parallèles, comme dans cet exemple, il peut être réduit par étapes en utilisant la stratégie de résolution de problèmes précédente et en considérant des groupes individuels de connexions en série ou en parallèle. Lors de\(R_{eq}\) la recherche d'une connexion parallèle, l'inverse doit être pris avec soin. De plus, les unités et les résultats numériques doivent être raisonnables. La résistance série équivalente doit être supérieure, tandis que la résistance parallèle équivalente doit être plus petite, par exemple. La puissance doit être supérieure pour les mêmes appareils en parallèle par rapport à ceux en série, etc.