10.4 : Les règles de Kirchhoff
- Page ID
- 190979
À la fin de la section, vous serez en mesure de :
- Règle de jonction de l'État de Kirchhoff
- Règle de la boucle d'État de Kirchhoff
- Analysez des circuits complexes en utilisant les règles de Kirchhoff
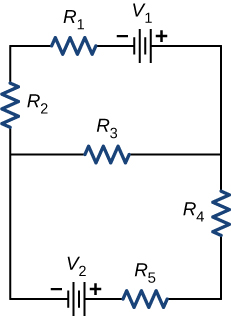
Nous venons de voir que certains circuits peuvent être analysés en réduisant un circuit à une seule source de tension et à une résistance équivalente. De nombreux circuits complexes ne peuvent pas être analysés à l'aide des techniques série-parallèle développées dans les sections précédentes. Dans cette section, nous expliquons plus en détail l'utilisation des règles de Kirchhoff pour analyser des circuits plus complexes. Par exemple, le circuit de la figure\(\PageIndex{1}\) est connu sous le nom de circuit à boucles multiples, composé de jonctions. Une jonction, également appelée nœud, est une connexion de trois fils ou plus. Dans ce circuit, les méthodes précédentes ne peuvent pas être utilisées, car toutes les résistances ne sont pas dans des configurations en série ou en parallèle claires pouvant être réduites. Essayez-le. Les résistances\(R_1\) et\(R_2\) B sont en série et peuvent être réduites à une résistance équivalente. Il en va de même pour les résistances\(R_4\) et\(R_5\). Mais que faites-vous alors ?
Même si ce circuit ne peut pas être analysé à l'aide des méthodes déjà apprises, deux règles d'analyse de circuit peuvent être utilisées pour analyser n'importe quel circuit, simple ou complexe. Les règles sont connues sous le nom de règles de Kirchhoff, d'après leur inventeur Gustav Kirchhoff (1824-1887).
- La première règle de Kirchhoff : la règle des jonctions. La somme de tous les courants entrant dans une jonction doit être égale à la somme de tous les courants sortant de la jonction :\[\sum I_{in} = \sum I_{out}.\]
- La deuxième règle de Kirchhoff : la règle de la boucle. La somme algébrique des changements de potentiel autour de tout circuit fermé (boucle) doit être nulle :\[\sum V = 0.\]
Nous fournissons maintenant des explications sur ces deux règles, suivies de conseils de résolution de problèmes pour les appliquer et d'un exemple concret qui les utilise.
La première règle de Kirchhoff
La première règle de Kirchhoff (la règle des jonctions) s'applique à la charge entrant et sortant d'une jonction (Figure\(\PageIndex{2}\)). Comme indiqué précédemment, une jonction, ou nœud, est une connexion de trois fils ou plus. Le courant est le flux de charge, et la charge est conservée ; ainsi, toute charge qui entre dans la jonction doit s'écouler vers l'extérieur.
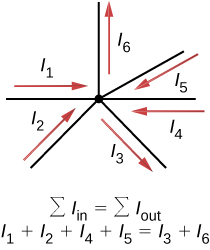
Bien qu'il s'agisse d'une simplification excessive, une analogie peut être faite avec des conduites d'eau raccordées dans un raccord de plomberie. Si les fils de la figure\(\PageIndex{2}\) ont été remplacés par des conduites d'eau et que l'eau a été supposée incompressible, le volume d'eau s'écoulant dans la jonction doit être égal au volume d'eau sortant de la jonction.
La deuxième règle de Kirchhoff
La deuxième règle de Kirchhoff (la règle de la boucle) s'applique aux différences potentielles. La règle de la boucle est énoncée en termes de potentiel V plutôt que d'énergie potentielle, mais les deux sont liés depuis\(U = qV\). En boucle fermée, quelle que soit l'énergie fournie par une source de tension, elle doit être transférée sous d'autres formes par les dispositifs de la boucle, car il n'existe aucun autre moyen de transférer de l'énergie vers ou hors du circuit. La règle de la boucle de Kirchhoff stipule que la somme algébrique des différences de potentiel, y compris la tension fournie par les sources de tension et les éléments résistifs, dans toute boucle doit être égale à zéro. Par exemple, considérez une boucle simple sans jonctions, comme dans la Figure\(\PageIndex{3}\).
Le circuit se compose d'une source de tension et de trois résistances de charge externes. Les étiquettes a, b, c et d servent de références et n'ont aucune autre signification. L'utilité de ces étiquettes sera bientôt évidente. La boucle est désignée comme Loop abcda, et les étiquettes permettent de suivre les différences de tension lorsque nous nous déplaçons dans le circuit. Commencez par le point a et continuez jusqu'au point b. La tension de la source de tension est ajoutée à l'équation et la chute de potentiel de la résistance\(R_1\) est soustraite. Du point b au point c, la chute potentielle\(R_2\) est soustraite. De c à d, la chute potentielle\(R_3\) est soustraite. Du point d au point a, rien n'est fait car il n'y a pas de composants.
La figure\(\PageIndex{4}\) montre un graphique de la tension lorsque nous nous déplaçons dans la boucle. La tension augmente lorsque nous traversons la batterie, tandis que la tension diminue lorsque nous traversons une résistance. La chute de potentiel, ou la variation du potentiel électrique, est égale au courant traversant la résistance multiplié par la résistance de la résistance. Comme les fils ont une résistance négligeable, la tension reste constante lorsque nous croisons les fils reliant les composants.
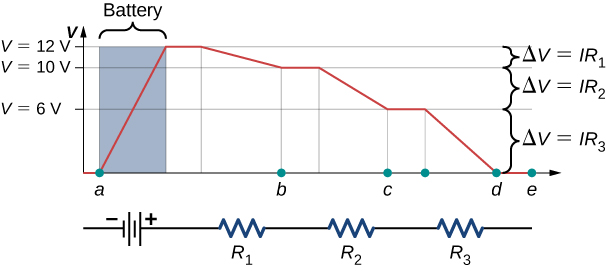
Ensuite, la règle de la boucle de Kirchhoff stipule
\[V - IR_1 - IR_2 - IR_3 = 0.\]
L'équation de la boucle peut être utilisée pour déterminer le courant dans la boucle :
\[I = \frac{V}{R_1 +R_2 +R_3} = \frac{12.00 \, V}{1.00 \, \Omega + 2.00 \, \Omega + 3.00 \, \Omega} = 2.00 \, A.\]
Cette boucle aurait pu être analysée à l'aide des méthodes précédentes, mais nous allons démontrer la puissance de la méthode de Kirchhoff dans la section suivante.
Appliquer les règles de Kirchhoff
En appliquant les règles de Kirchhoff, nous générons un ensemble d'équations linéaires qui nous permettent de trouver les valeurs inconnues dans les circuits. Il peut s'agir de courants, de tensions ou de résistances. Chaque fois qu'une règle est appliquée, elle produit une équation. S'il y a autant d'équations indépendantes que d'inconnues, le problème peut être résolu.
L'utilisation de la méthode d'analyse de Kirchhoff nécessite plusieurs étapes, comme indiqué dans la procédure suivante.
- Étiquetez les points du schéma en utilisant des lettres minuscules a, b, c,... Ces étiquettes aident simplement à l'orientation.
- Localisez les jonctions du circuit. Les jonctions sont des points où trois fils ou plus se connectent. Étiquetez chaque jonction avec les courants et les directions d'entrée et de sortie. Assurez-vous qu'au moins un courant pointe dans la jonction et qu'au moins un courant pointe hors de la jonction.
- Choisissez les boucles du circuit. Chaque composant doit être contenu dans au moins une boucle, mais un composant peut être contenu dans plusieurs boucles.
- Appliquez la règle de jonction. Encore une fois, certaines jonctions ne doivent pas être incluses dans l'analyse. Vous n'avez qu'à utiliser suffisamment de nœuds pour inclure tous les courants.
- Appliquez la règle de boucle. Utilisez la carte de la figure\(\PageIndex{5}\).
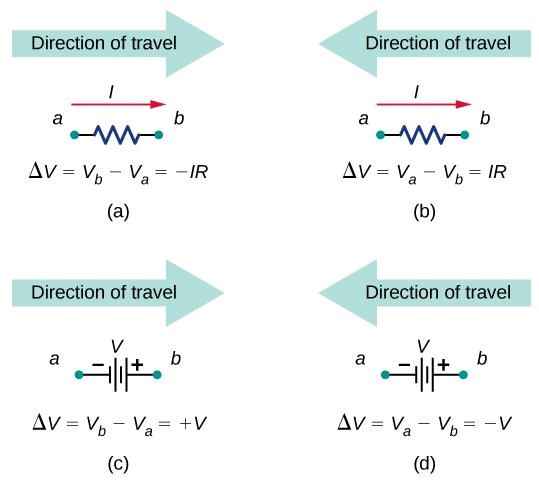
Examinons de plus près certaines étapes de cette procédure. Lorsque vous localisez les jonctions dans le circuit, ne vous inquiétez pas de la direction des courants. Si le sens du flux de courant n'est pas évident, il suffit de choisir n'importe quelle direction tant qu'au moins un courant pointe dans la jonction et au moins un courant hors de la jonction. Si la flèche est dans le sens opposé au flux de courant conventionnel, le résultat pour le courant en question sera négatif mais la réponse sera toujours correcte.
Le nombre de nœuds dépend du circuit. Chaque courant doit être inclus dans un nœud et donc inclus dans au moins une équation de jonction. N'incluez pas les nœuds qui ne sont pas linéairement indépendants, c'est-à-dire les nœuds qui contiennent les mêmes informations.
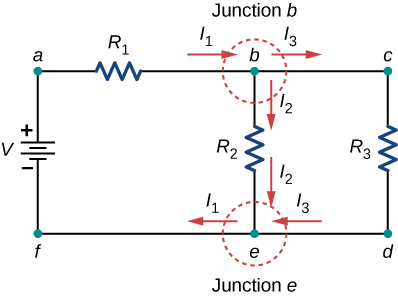
Considérez Figure\(\PageIndex{6}\). Ce circuit comporte deux jonctions : la jonction b et la jonction e. Les points a, c, d et f ne sont pas des jonctions, car une jonction doit avoir trois connexions ou plus. L'équation de la jonction b est\(I_1 = I_2 + I_3\), et l'équation de la jonction e est\(I_2 + I_3 = I_1\). Ce sont des équations équivalentes, il est donc nécessaire de n'en conserver qu'une seule.
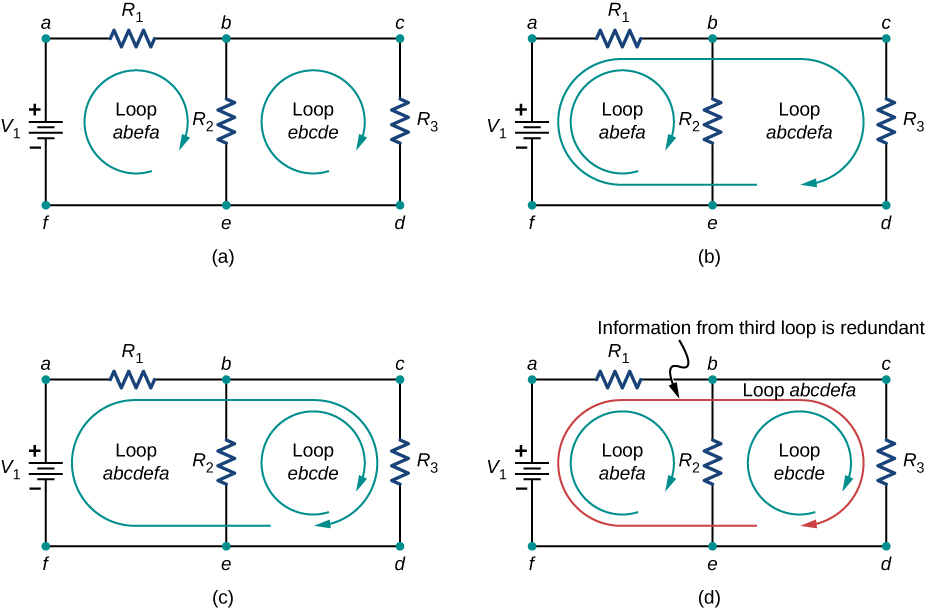
Lorsque vous choisissez les boucles du circuit, vous avez besoin de suffisamment de boucles pour que chaque composant soit couvert une fois, sans répéter les boucles. La figure\(\PageIndex{7}\) montre quatre choix de boucles pour résoudre un exemple de circuit ; les choix (a), (b) et (c) comportent un nombre de boucles suffisant pour résoudre complètement le circuit. L'option (d) reflète plus de boucles que nécessaire pour résoudre le circuit.
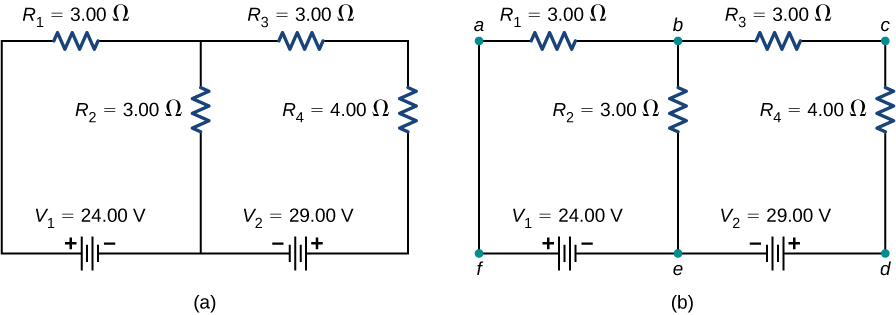
Considérez le circuit de la figure\(\PageIndex{8a}\). Analysons ce circuit pour trouver le courant traversant chaque résistance. Tout d'abord, étiquetez le circuit comme indiqué dans la partie (b).
Ensuite, déterminez les jonctions. Dans ce circuit, les points b et e ont chacun trois fils connectés, ce qui en fait des jonctions. Commencez à appliquer la règle de jonction de Kirchhoff\(\left(\sum I_{in} = \sum I_{out}\right)\) en dessinant des flèches représentant les courants et en étiquetant chaque flèche, comme indiqué sur la figure\(\PageIndex{9}\). La jonction B le montre\(I_1 = I_2 + I_3\) et la jonction e le montre\(I_2 + I_3 = I_1\). Puisque la jonction e donne les mêmes informations que la jonction b, elle peut être ignorée. Ce circuit comporte trois inconnues, nous avons donc besoin de trois équations linéairement indépendantes pour l'analyser.

Ensuite, nous devons choisir les boucles. Sur la figure\(\PageIndex{10}\), la boucle abefa inclut la source de tension\(V_1\) et les résistances\(R_1\) et\(R_2\). La boucle commence au point a, puis passe par les points b, e et f, puis revient au point a. La deuxième boucle, Loop ebcde, commence au point e et comprend les résistances\(R_2\) et\(R_3\), et la source de tension\(V_2\).
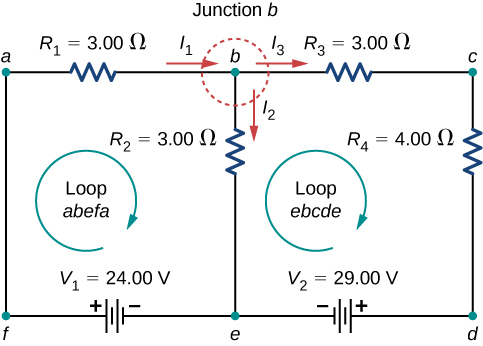
Nous pouvons maintenant appliquer la règle de boucle de Kirchhoff, en utilisant la carte de la Figure\(\PageIndex{5}\). En partant du point a et en se déplaçant vers le point b, la résistance\(R_1\) est traversée dans le même sens que le courant\(I_1\), de sorte que la chute de potentiel\(I_1R_1\) est soustraite. En se déplaçant du point b au point e, la résistance\(R_2\) est traversée dans le même sens que le courant, de\(I_2\) sorte que la chute de potentiel\(I_2R_2\) est soustraite. En passant du point e au point f, la source de tension\(V_1\) est traversée de la borne négative à la borne positive, elle\(V_1\) est donc ajoutée. Il n'y a aucune composante entre les points f et a. La somme des différences de tension doit être égale à zéro :
\[Loop \, abefa: \, -I_1R_1 - I_2R_2 + V_1 = 0 \, or \, V_1 = I_1R_1 + I_2R_2.\]
Enfin, nous vérifions la boucle ebcde. Nous partons du point e et nous nous dirigeons vers le point b,\(R_2\) en traversant dans la direction opposée à celle du courant\(I_2\). La baisse potentielle\(I_2R_2\) est ajoutée. Ensuite, nous traversons\(R_3\) et\(R_4\) dans le même sens que le flux de courant\(I_3\) et soustrayons les chutes de potentiel\(I_3R_3\) et\(I_3R_4\). Notez que le courant est le même à travers les résistances\(R_3\) et\(R_4\) parce qu'elles sont connectées en série. Enfin, la source de tension passe de la borne positive à la borne négative, et la source de tension\(V_2\) est soustraite. La somme de ces différences de tension est égale à zéro et donne l'équation de la boucle
\[Loop \, ebcde: \, I_2R_2 - I_3(R_3 + R_4) - V_2 = 0.\]
Nous avons maintenant trois équations que nous pouvons résoudre pour les trois inconnues.
\[\text{Junction b:} \, I_1 - I_2 - I_3 = 0. \label{eq1}\]
\[\text{Loop abefa:} \, I_1R_1 + I_2R_2 = V_1. \label{eq2}\]
\[\text{Loop ebcde:} \, I_2R_2 - I_3(R_3 + R_4) = V_2. \label{eq3}\]
Pour résoudre les trois équations des trois courants inconnus, commencez par éliminer le courant\(I_2\). Ajoutez d'abord l'équation \ ref {eq1} fois\(R_2\) à l'équation \ ref {eq2}. Le résultat est l'équation \ ref {eq4} :
\[(R_1 + R_2) I_1 - R_2I_3 = V_1.\]
\[6 \, \Omega I_1 - 3 \Omega I_3 = 24 \, V. \label{eq4}\]
Ensuite, soustrayez l'équation \ ref {eq3} de l'équation \ ref {eq2}. Le résultat est l'équation \ ref {eq5} :
\[I_1R_1 + I_3(R_3 + R_4) = V_1 - V_2.\]
\[3 \Omega I_1 + 7 \Omega I_3 = -5 \, V. \label{eq5}\]
Nous pouvons résoudre les équations \ ref {eq4} et \ ref {eq5} pour le courant\(I_1\). L'ajout de sept fois l'équation \ ref {eq4} et de trois fois l'équation \ ref {eq5} donne\(51 \, \Omega I_1 = 153 \, V\), ou\(I_1 = 3.00 \, A\). L'utilisation de l'équation \ ref {eq4} aboutit à\(I_3 = -2.00 \, A\). Enfin, l'équation \ ref {eq1} donne\(I_2 = I_1 - I_3 = 5.00 \, A\). Une façon de vérifier la cohérence des solutions consiste à vérifier la puissance fournie par les sources de tension et la puissance dissipée par les résistances :
\[P_{in} = I_1V_1 + I_3V_2 = 130 \, W, \nonumber\]
\[P_{out} = I_1^2R_1 + I_2^2R_2 + I_3^2R_3 + I_3^2R_4 = 130 \, W. \nonumber\]
Notez que la solution pour le courant\(I_3\) est négative. C'est la bonne réponse, mais cela suggère que la flèche dessinée à l'origine dans l'analyse des jonctions est dans la direction opposée au flux de courant conventionnel. La puissance fournie par la deuxième source de tension est de 58 W et non de -58 W.
Déterminez les courants circulant dans le circuit sur la figure\(\PageIndex{11}\).
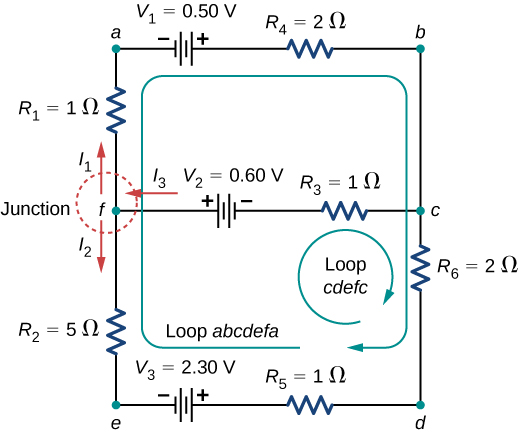
Stratégie
Ce circuit est suffisamment complexe pour que les courants ne puissent pas être détectés à l'aide de la loi d'Ohm et des techniques série-parallèle ; il est nécessaire d'utiliser les règles de Kirchhoff. Les courants ont été étiquetés\(I_1, \, I_2\), et\(I_3\) dans la figure, et des hypothèses ont été émises quant à leur direction. Les emplacements sur le diagramme ont été étiquetés avec les lettres a à h. Dans la solution, nous appliquons les règles de jonction et de boucle, en recherchant trois équations indépendantes pour nous permettre de résoudre les trois courants inconnus.
Solution
L'application des règles de jonction et de boucle produit les trois équations suivantes. Nous avons trois inconnues, donc trois équations sont nécessaires.
\[Junction \, c: \, I_1 + I_2 = I_3.\]
\[Loop \, abcdefa: \, I_1(R_1 + R_4) - I_2(R_2 + R_5 + R_6) = V_1 - V_3.\]
\[Loop \, cdefc: \, I_2(R_2 + R_5 + R_6) + I_3R_3 = V_2 + V_3.\]
Simplifiez les équations en plaçant les inconnues d'un côté des équations.
\[Junction \, c: \, I_1 + I_2 - I_3 = 0.\]
\[Loop \, abcdefa: \, I_1 (3 \Omega) - I_2(8 \Omega) = 0.5 \, V - 2.30 \, V.\]
\[Loop \, cdefc: \, I_2 (8 \Omega) + I_3 (1 \Omega) = 0.6 \, V + 2.30 \, V.\]
Simplifiez les équations. La première équation en boucle peut être simplifiée en divisant les deux côtés par 3,00. La deuxième équation de boucle peut être simplifiée en divisant les deux côtés par 6,00.
\[Junction \, c: \, I_1 + I_2 - I_3 = 0.\]
\[Loop \, abcdefa: \, I_1 (3 \Omega) - I_2(8 \Omega) = - 1.8 \, V.\]
\[Loop \, cdefc: \, I_2 (8 \Omega) + I_3 (1 \Omega) = 2.90 \, V.\]
Les résultats sont
\[I_1 = 0.20 \, A, \, I_2 = 0.30 \, A, \, I_3 = 0.50 \, A.\]
L'importance
Une méthode pour vérifier les calculs consiste à calculer la puissance dissipée par les résistances et la puissance fournie par les sources de tension :
\[P_{R_1} = I_1^2R_1 = 0.04 \, W.\]
\[P_{R_2} = I_2^2R_2 = 0.45 \, W.\]
\[P_{R_3} = I_3^2R_3 = 0.25 \, W.\]
\[P_{R_4} = I_1^2R_4 = 0.08 \, W.\]
\[P_{R_5} = I_2^2R_5 = 0.09 \, W.\]
\[P_{R_6} = I_2^2R_1 = 0.18 \, W.\]
\[P_{dissipated} = 1.09 \, W.\]
\[P_{source} = I_1V_1 + I_2V_3 + I_3V_2 = 0.10 \, + 0.69 \, W + 0.30 \, W = 1.09 \, W.\]
La puissance fournie est égale à la puissance dissipée par les résistances.
Si l'on considère le schéma suivant et l'énergie fournie et consommée par un circuit, une source de tension fournira-t-elle toujours de l'énergie au circuit ou une source de tension peut-elle consommer de l'énergie ?
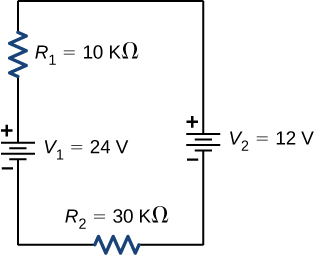
- Réponse
-
Le circuit peut être analysé à l'aide de la règle de boucle de Kirchhoff. La première source de tension fournit de l'énergie :
Contributors and Attributions


