9.3 : Spectres moléculaires
- Page ID
- 189524
À la fin de cette section, vous serez en mesure de :
- Utiliser les concepts d'énergie vibratoire et rotationnelle pour décrire les transitions énergétiques dans une molécule diatomique
- Expliquer les principales caractéristiques du spectre énergétique vibrationnel-rotationnel d'une molécule diatomique
- Estimer les énergies autorisées d'une molécule en rotation
- Déterminer la distance de séparation d'équilibre entre les atomes d'une molécule diatomique à partir du spectre d'absorption vibrationnelle-rotationnelle
Les niveaux d'énergie moléculaire sont plus complexes que les niveaux d'énergie atomique car les molécules peuvent également vibrer et tourner. Les énergies associées à de tels mouvements se situent dans différentes plages et peuvent donc être étudiées séparément. Les transitions électroniques sont d'ordre 1 eV, les transitions vibratoires sont d'ordre et\(10^{-2}eV\) les transitions rotationnelles sont d'ordre\(10^{-3}eV\). Pour les molécules complexes, ces changements d'énergie sont difficiles à caractériser. Nous commençons donc par le cas simple d'une molécule diatomique.
Rotation quantique
Selon la mécanique classique, l'énergie de rotation d'une molécule diatomique est donnée par
\[E_r = \dfrac{L^2}{2I}, \nonumber \]
où I est le moment d'inertie et L est le moment cinétique. Selon la mécanique quantique, le moment cinétique de rotation est quantifié :
\[L = \sqrt{l(l + 1)} \hbar (l = 0,1,2,3,...), \nonumber \]
où l est le nombre quantique angulaire orbital. Le niveau d'énergie de rotation autorisé d'une molécule diatomique est donc
\[E_r = l(l + 1) \dfrac{\hbar^2}{2I} = l(l + 1) \, E_{0r} \, \, (l = 0,1,2,3,...), \nonumber \]
où l'énergie de rotation caractéristique d'une molécule est définie comme
\[E_{0r} = \dfrac{\hbar^2}{2I}. \nonumber \]
Pour une molécule diatomique, le moment d'inertie à masse réduite\(μ\) est
\[I = \mu r_0^2, \nonumber \]
où\(r_0\) est la distance totale entre les atomes. La différence d'énergie entre les niveaux de rotation est donc
\[\Delta E_r = E_{l+1} - E_l = 2(l + 1) \, E_{0r}. \nonumber \]
Une étude détaillée des transitions entre les niveaux d'énergie de rotation provoquées par l'absorption ou l'émission de rayonnement (transition dite dipolaire électrique) nécessite que
\[\Delta l = \pm1. \label{delta l} \]
Cette règle, appelée règle de sélection, limite les transitions possibles d'un état quantique à un autre. L'équation \ ref {delta l} est la règle de sélection pour les transitions énergétiques rotationnelles. Elle s'applique uniquement aux molécules diatomiques qui ont un moment dipolaire électrique. Pour cette raison, les molécules symétriques telles que\(H_2\) et\(N_2\) ne subissent pas de transitions énergétiques rotationnelles dues à l'absorption ou à l'émission de rayonnements électromagnétiques.
Déterminez les trois niveaux d'énergie de rotation les plus faibles d'une molécule de chlorure d'hydrogène ((\(\ce{HCl}\))).
Stratégie
Le chlorure d'hydrogène (\(\ce{HCl}\)) est une molécule diatomique dont la distance de séparation à l'équilibre est de 0,127 nm. Les niveaux d'énergie de rotation dépendent uniquement du moment d'inertie I et du nombre quantique du moment cinétique orbital\(l\) (dans ce cas\(l = 0\), 1 et 2). Le moment d'inertie dépend à son tour de la distance de séparation d'équilibre (qui est donnée) et de la masse réduite, qui dépend des masses des atomes de H et de Cl.
Solution
Nous calculons d'abord la masse réduite. Si la particule 1 est de l'hydrogène et la particule 2 est du chlorure, nous avons
\[\begin{align*} \mu &= \dfrac{m_1m_2}{m_1 + m_2} = \dfrac{(1.0 \, u)(35.4 \, u)}{1.0 \, u + 35.4 \, u} \\[4pt] &= 0.97 \, u = 0.97 \, u \left(\dfrac{931.5 \dfrac{MeV}{c^2}}{1 \, u}\right) \\[4pt] &= 906 \dfrac{MeV}{c^2}. \end{align*} \nonumber \]
L'énergie massique de repos correspondante est donc
\[\mu c^2 = 9.06 \times 10^8 \, eV \nonumber \]
Cela nous permet de calculer l'énergie caractéristique :
\[ \begin{align*} E_{0r} &= \dfrac{\hbar^2}{2(\mu r_0^2)} = \dfrac{(\hbar c)^2}{2(\mu c^2)r_0^2} \nonumber \\[4pt] &= \dfrac{(197.3 \, eV \cdot nm)^2}{2(9.06 \times 10^8 eV)(0.127 \, nm)^2} \nonumber \\[4pt] &= 1.33 \times 10^{-3} eV. \nonumber \end{align*} \nonumber \]
(Remarquez comment cette expression est écrite en termes d'énergie massique restante. Cette technique est courante dans les calculs physiques modernes.) Les niveaux d'énergie de rotation sont donnés par
\[E_r = l(l + 1) \dfrac{\hbar^2}{2I} = l(l + 1) E_{0r}, \nonumber \]
où\(l\) est le nombre quantique orbital. Les trois niveaux d'énergie rotationnelle les plus faibles d'une molécule de HCl sont donc
\[\begin{align*} l &= 0:\quad E_r &&= 0 \, eV \, \text{(no rotation)} \\[4pt] l &= 1: \quad E_r &&= 2 \, E_{0r} = 2.66 \times 10^{-3}eV, \\[4pt] l &= 2:\quad E_r &&= 6 \, E_{0r} = 7.99 \times 10^{-3} eV. \end{align*} \nonumber \]
L'importance
Le spectre rotationnel est associé à de faibles transitions (1/1000 à 1/100 d'eV). En comparaison, l'énergie d'un électron à l'état fondamental de l'hydrogène est de\(- 13.6 \, eV\).
Que vous apprend la séparation énergétique entre les raies d'absorption dans le spectre de rotation d'une molécule diatomique ?
- Réponse
-
le moment d'inertie
Vibration quanti
Le niveau d'énergie vibratoire, qui est le niveau d'énergie associé à l'énergie vibratoire d'une molécule, est plus difficile à estimer que le niveau d'énergie rotationnelle. Cependant, nous pouvons estimer ces niveaux en supposant que les deux atomes de la molécule diatomique sont reliés par un ressort idéal de constante de ressort k. L'énergie potentielle de ce système de ressort est
\[U_{osc} = \dfrac{1}{2}k \Delta r^2, \nonumber \]
Où\(\Delta r\) se produit une modification de la « longueur naturelle » de la molécule le long d'une ligne qui relie les atomes. La résolution de l'équation de Schrödinger pour ce potentiel donne
\[E_n = \left(n + \dfrac{1}{2}\right) \hbar \omega \, (n = 0,1,2,. . .), \nonumber \]
Où\(\omega\) est la fréquence angulaire naturelle de la vibration et n est le nombre quantique vibrationnel. La prédiction selon laquelle les niveaux d'énergie vibratoire sont régulièrement espacés (\(\Delta E = \hbar \omega\)) s'avère bonne à des énergies plus faibles.
Une étude détaillée des transitions entre les niveaux d'énergie vibratoire induits par l'absorption ou l'émission de rayonnement (et la transition dipolaire spécifiquement appelée transition électrique) nécessite que
\[\Delta n = \pm 1. \label{delta n} \]
L'équation \ ref {delta n} représente la règle de sélection pour les transitions d'énergie vibratoire. Comme mentionné précédemment, cette règle s'applique uniquement aux molécules diatomiques qui ont un moment dipolaire électrique. Les molécules symétriques ne connaissent pas de telles transitions.
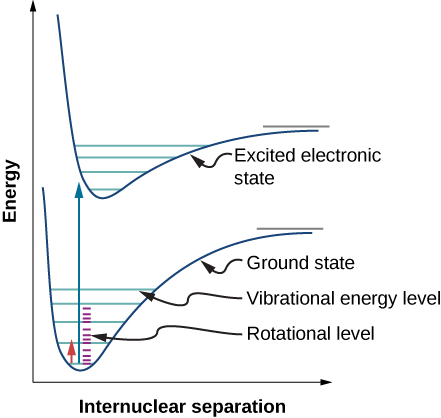
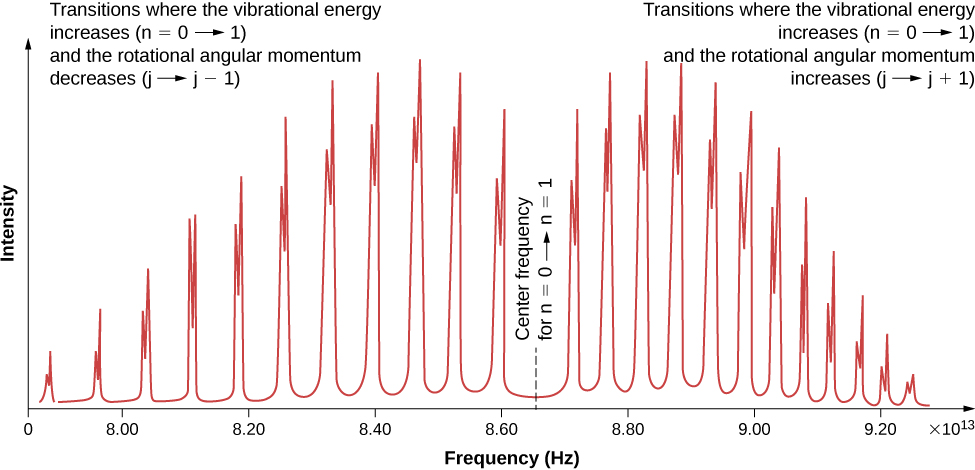
En raison des règles de sélection, l'absorption ou l'émission de rayonnement par une molécule diatomique implique une transition entre les états vibratoire et rotationnel. Plus précisément, si le nombre quantique vibratoire (n) change d'une unité, alors le nombre quantique rotationnel (l) change d'une unité. Un diagramme de niveau d'énergie d'une transition possible est donné dans la figure\(\PageIndex{1}\). Le spectre d'absorption de telles transitions dans le chlorure d'hydrogène (HCl) est illustré dans la Figure (\ PageIndex {2} \). Les pics d'absorption sont dus à des transitions entre les\(n = 0\) états vibratoires et les états\(n = 1\) vibratoires. Les différences d'énergie pour la bande de pics à gauche et à droite sont respectivement les suivantes :
(bande droite)
\[ \Delta E_{l \rightarrow l+1} = \hbar \omega + 2(l + 1)E_{0r} = \hbar \omega + 2E_{0r}, \, \hbar \omega + 4E_{0r}, \, \hbar \omega + 6E_{0r}, ... \nonumber \]
(bande gauche)
\[ \Delta E_{l \rightarrow l-1} = \hbar \omega - 2l E_{0r} = \hbar \omega - 2E_{0r}, \, \hbar \omega - 4E_{0r}, \, \hbar \omega - 6E_{0r}, .... \nonumber \]
Le moment d'inertie peut ensuite être déterminé à partir de l'espacement énergétique entre les pics individuels (\(2E_{0r}\)) ou à partir de l'écart entre les bandes gauche et droite (\(4E_{0r}\)). La fréquence au centre de cet espace est la fréquence des vibrations.