7.3 : Le principe d'incertitude de Heisenberg
- Page ID
- 189860
À la fin de cette section, vous serez en mesure de :
- Décrire la signification physique de la relation d'incertitude position-moment
- Expliquer les origines du principe d'incertitude en théorie quantique
- Décrire la signification physique de la relation d'incertitude énergie-temps
Le principe d'incertitude de Heisenberg est un principe clé de la mécanique quantique. Très grossièrement, il indique que si nous savons tout sur l'emplacement d'une particule (l'incertitude de position est faible), nous ne savons rien de sa quantité de mouvement (l'incertitude de la quantité de mouvement est grande), et vice versa. Des versions du principe d'incertitude existent également pour d'autres grandeurs, telles que l'énergie et le temps. Nous discutons séparément des principes de la position du moment et de l'incertitude énergie-temps.
Moment et position
Pour illustrer le principe d'incertitude entre la quantité de mouvement et la position, considérez une particule libre qui se déplace le long de la direction x. La particule se déplace avec une vitesse\(u\) et une quantité de mouvement constantes\(p = mu\). Selon les relations de de Broglie,\(p = \hbar k\) et\(E = \hbar \omega\). Comme indiqué dans la section précédente, la fonction d'onde d'une particule libre est donnée par
\[ \begin{align*} \psi_k(x,t) &= A[\cos \, (\omega t - kx) - i \, \sin \, (\omega t - kx)] \\[4pt] &= A \, e^{-i(\omega t - kx)} \\[4pt] &= A \, e^{-i(\omega t - kx)} \\[4pt] &=A\, e^{-i\omega t} e^{ikx} \end{align*} \nonumber \]
et la densité de probabilité\(|\psi_k (x,t)|^2 = A^2\) est uniforme et indépendante du temps. La particule est également susceptible de se trouver n'importe où le long de l'axe x, mais elle possède des valeurs définies de longueur d'onde et de nombre d'ondes, et donc de moment. L'incertitude de position est infinie (nous sommes totalement incertains quant à la position) et l'incertitude de la dynamique est nulle (nous sommes totalement certains de la dynamique). Cette description d'une particule libre est conforme au principe d'incertitude de Heisenberg.
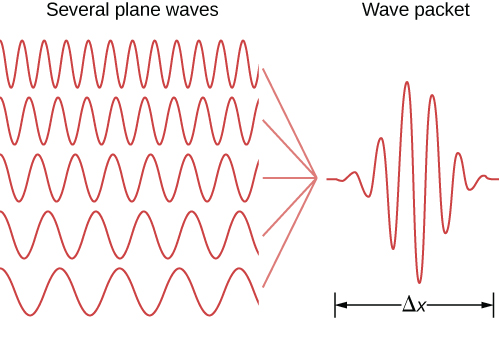
Des déclarations similaires peuvent être faites à propos de particules localisées. En théorie quantique, une particule localisée est modélisée par une superposition linéaire d'états de particules libres (ou ondes planes) appelée paquet d'ondes. Un exemple de paquet d'ondes est illustré dans la figure\(\PageIndex{1}\). Un paquet d'ondes contient de nombreuses longueurs d'onde et donc, selon les relations de Broglie, de nombreux moments, ce qui est possible en mécanique quantique ! Cette particule possède également de nombreuses valeurs de position, bien que la particule soit principalement confinée dans l'intervalle\(\Delta x\). La particule peut être mieux localisée (\(\Delta x\)peut être diminuée) si davantage d'états d'ondes planes de différentes longueurs d'onde ou de différents moments sont additionnés de la bonne manière (elle\(\Delta p\) est augmentée). Selon Heisenberg, ces incertitudes obéissent à la relation suivante.
Le produit de l'incertitude quant à la position d'une particule et de l'incertitude quant à sa quantité de mouvement ne peut jamais être inférieur à la moitié de la constante de Planck réduite :
\[\Delta x \Delta p \geq \dfrac{\hbar}{2}. \label{Heisen} \]
Cette relation exprime le principe d'incertitude de Heisenberg. Il impose des limites à ce que nous pouvons savoir sur une particule à partir de mesures simultanées de position et de moment. Elle\(\Delta x\) est grande, elle\(\Delta p\) est petite et vice versa. L'équation \ ref {Heisen} peut être dérivée dans un cours plus avancé de physique moderne. Réfléchissant à cette relation dans son ouvrage The Physical Principles of the Quantum Theory, Heisenberg a écrit : « Toute utilisation des mots « position » et « vitesse » avec une précision supérieure à celle donnée par [la relation] est tout aussi vide de sens que l'utilisation de mots dont le sens n'est pas défini ».
Notez que le principe d'incertitude n'a rien à voir avec la précision d'un appareil expérimental. Même pour des appareils de mesure parfaits, ces incertitudes persisteraient car elles proviennent de la nature ondulatoire de la matière. La valeur précise du produit\(\Delta x \Delta p\) dépend de la forme spécifique de la fonction d'onde. Il est intéressant de noter que la fonction gaussienne (ou distribution de la courbe en cloche) donne la valeur minimale du produit d'incertitude :
\[\Delta x \Delta p = \dfrac{\hbar}{2} \nonumber \]
Déterminer les incertitudes minimales concernant la position des objets suivants si leur vitesse est connue avec une précision de\(1.0 \times 10^{-3} m/s\) :
- un électron et
- une boule de bowling d'une masse de 6,0 kg.
Stratégie
Compte tenu de l'incertitude liée à la vitesse\(\Delta u = 1.0 \times 10^{-3} m/s\), nous devons d'abord déterminer l'incertitude de la quantité de mouvement,\(\Delta p = m\Delta u\) puis inverser l'équation \ ref {Heisen} pour trouver l'incertitude en position
\[\Delta x = \dfrac{\hbar}{2\Delta p}. \nonumber \]
Solution
- Pour l'électron :\[\begin{align*} \Delta p &= m\Delta u \\[4pt] &= (9.1 \times 10^{-31} kg)(1.0 \times 10^{-3}m/s) \\[4pt] &= 9.1 \times 10^{-34} kg \cdot m/s,\end{align*} \nonumber \]\[\begin{align*} \Delta x &= \frac{\hbar}{2\Delta p} \\[4pt] &= 5.8 \, cm. \end{align*} \nonumber \]
- Pour la boule de bowling :\[\begin{align*} \Delta p &= m\Delta u \\[4pt] &= (6.0 \, kg)(1.0 \times 10^{-3}m/s) \\[4pt] &= 6.0 \times 10^{-3} kg \cdot m/s, \end{align*} \nonumber \]\[\begin{align*} \Delta x &= \frac{\hbar}{2\Delta p} \\[4pt] &= 8.8 \times 10^{-33}m. \end{align*} \nonumber \]
L'importance
Contrairement à l'incertitude de position de l'électron, l'incertitude de position de la boule de bowling est incommensurablement faible. La constante de Planck étant très faible, les limites imposées par le principe d'incertitude ne sont pas perceptibles dans les systèmes macroscopiques tels qu'une boule de bowling.
Estimez l'énergie fondamentale d'un atome d'hydrogène en utilisant le principe d'incertitude de Heisenberg. (Conseil : selon les premières expériences, la taille d'un atome d'hydrogène est d'environ 0,1 nm.)
Stratégie
Un électron lié à un atome d'hydrogène peut être modélisé par une particule liée à une boîte unidimensionnelle de longueur\(L = 0.1 \, nm\). La fonction d'onde de l'état fondamental de ce système est une demi-onde. Il s'agit de la plus grande longueur d'onde pouvant « rentrer » dans la boîte, de sorte que la fonction d'onde correspond à l'état d'énergie le plus bas. Notez que la forme de cette fonction est très similaire à celle d'une fonction gaussienne (courbe en cloche). Nous pouvons prendre l'énergie moyenne d'une particule décrite par cette fonction (E) comme une bonne estimation de l'énergie de l'état fondamental (\(E_0\)). Cette énergie moyenne d'une particule est liée à sa moyenne de la quantité de mouvement au carré, qui est liée à son incertitude de moment.
Solution
Pour résoudre ce problème, nous devons préciser ce que l'on entend par « incertitude de position » et « incertitude de dynamique ». Nous identifions l'incertitude de position (Δx) avec l'écart type de la position (\(σ_x\)), et l'incertitude de la quantité de mouvement (\(Δp\)) avec l'écart type de la quantité de mouvement (\(σ_p\)). Pour la fonction gaussienne, le produit d'incertitude est
\[\sigma_x\sigma_p = \frac{\hbar}{2}, \nonumber \]
où
\[\sigma_x^2 = x^2 - \overline{x}^2 \nonumber \]
et
\[\sigma_p^2 = p^2 - \overline{p}^2.\nonumber \]
La particule est tout aussi susceptible de se déplacer vers la gauche que vers la droite, donc\(\overline{p}^2 = 0\). De plus, l'incertitude de position est comparable à la taille de la boîte, donc\(\sigma_x = L\). L'énergie estimée de l'état du sol est donc
\[\begin{align*} E_0 &= E_{Gaussian} \\[4pt] &= \dfrac{\overline{p}^2}{m} \\[4pt] &= \frac{\sigma_p^2}{2m} \\[4pt] &= \frac{1}{2m} \left(\frac{\hbar}{2\sigma_x}\right)^2 \\[4pt] &= \frac{1}{2m} \left(\frac{\hbar}{2L}\right)^2 \\[4pt] &= \frac{\hbar^2}{8mL^2}. \end{align*} \nonumber \]
\[\begin{align*}E_0 &= \dfrac{(\hbar c)^2}{8(mc^2)L^2} \\[4pt] &= \frac{(197.3 \, eV \cdot nm)^2}{8(0.511 \cdot 10^6 eV)(0.1 \, nm)^2} \\[4pt] &= 0.952 \, eV \approx 1 \, eV. \end{align*} \nonumber \]
Multiplier le numérateur et le dénominateur par des\(c^2\) données
L'importance
Sur la base des premières estimations de la taille d'un atome d'hydrogène et du principe d'incertitude, l'énergie fondamentale d'un atome d'hydrogène se situe dans la gamme eV. L'énergie d'ionisation d'un électron dans l'énergie de l'état fondamental est d'environ 10 eV, de sorte que cette prédiction est approximativement confirmée. (Remarque : Le produit cc est souvent une valeur utile pour effectuer des calculs en mécanique quantique.)
Énergie et temps
Un autre type de principe d'incertitude concerne les incertitudes liées aux mesures simultanées de l'énergie d'un état quantique et de sa durée de vie,
\[\Delta E \Delta t \geq \frac{\hbar}{2} \label{H2} \]
où\(\Delta E\) est l'incertitude de la mesure de l'énergie et\(\Delta t\) l'incertitude de la mesure de la durée de vie. Le principe d'incertitude énergie-temps ne résulte pas d'une relation du type exprimé par l'équation \ ref {Heisen} pour des raisons techniques allant au-delà de cette discussion. Néanmoins, la signification générale du principe énergie-temps est qu'un état quantique qui n'existe que depuis peu de temps ne peut pas avoir d'énergie définie. La raison en est que la fréquence d'un état est inversement proportionnelle au temps et que la fréquence est connectée à l'énergie de l'état. Par conséquent, pour mesurer l'énergie avec une bonne précision, l'état doit être observé pendant de nombreux cycles.
Pour illustrer, considérez les états excités d'un atome. Les durées de vie finies de ces états peuvent être déduites des formes des raies spectrales observées dans les spectres d'émission atomique. Chaque fois qu'un état excité décroît, l'énergie émise est légèrement différente et, par conséquent, la raie d'émission est caractérisée par une distribution des fréquences spectrales (ou longueurs d'onde) des photons émis. Par conséquent, toutes les raies spectrales sont caractérisées par des largeurs spectrales. L'énergie moyenne du photon émis correspond à l'énergie théorique de l'état excité et donne la localisation spectrale du pic de la raie d'émission. Les états de courte durée ont de larges largeurs spectrales et les états de longue durée de vie ont des largeurs spectrales étroites.
Un atome existe généralement dans un état excité depuis environ\(\Delta t = 10^{-8} s\). Estimez l'incertitude quant\(\Delta f\) à la fréquence des photons émis lorsqu'un atome passe d'un état excité avec l'émission simultanée d'un photon dont la fréquence moyenne est de\(f = 7.1 \times 10^{14} Hz\). Le rayonnement émis est-il monochromatique ?
Stratégie
Nous inversons l'équation \ ref {H2} pour obtenir l'incertitude énergétique\(\Delta E \approx \hbar /2\Delta t\) et la combinons avec l'énergie des photons\(E = hf\) pour obtenir\(\Delta f\). Pour estimer si l'émission est monochromatique ou non, nous évaluons\(\Delta f/f\).
Solution
La propagation des énergies des photons est\(\Delta E = h \Delta f\). Par conséquent,
\[\Delta E \approx \frac{\hbar}{2 \Delta t} \Rightarrow h \Delta t \approx \frac{\hbar}{2 \Delta t} \Rightarrow \Delta f \approx \frac{1}{4\pi \Delta t} = \frac{1}{4\pi (10^{-8}s)} = 8.0 \times 10^6 \, Hz, \nonumber \]
\[\frac{\Delta f}{f} = \frac{8.0 \times 10^6 \, Hz}{7.1 \times 10^{14} \, Hz} = 1.1 \times 10^{-8}. \nonumber \]
L'importance
Comme les photons émis ont des fréquences inférieures à un\(1.1 \times 10^{-6}\) pourcentage de la fréquence moyenne, le rayonnement émis peut être considéré comme monochromatique.
Un atome de sodium passe du premier état excité à l'état fondamental, émettant un photon de 589,0 nm d'une énergie de 2,105 eV. Si la durée de vie de cet état excité est\(1.6 \times 10^{-8} s\), quelle est l'incertitude énergétique de cet état excité ? Quelle est la largeur de la raie spectrale correspondante ?
- Réponse
-
\(4.1 \times 10^{-8} eV\);\(1.1 \times 10^{-5} nm\)


