7.2 : Fonctions ondulatoires
- Page ID
- 189894
À la fin de cette section, vous serez en mesure de :
- Décrire l'interprétation statistique de la fonction d'onde
- Utiliser la fonction d'onde pour déterminer les probabilités
- Calculez les valeurs attendues de position, de moment et d'énergie cinétique
Dans le chapitre précédent, nous avons vu que les particules agissent dans certains cas comme des particules et dans d'autres cas comme des ondes. Mais que signifie pour une particule « agir comme une onde » ? Qu'est-ce que « faire signe » exactement ? Quelles règles régissent la façon dont cette vague change et se propage ? Comment la fonction d'onde est-elle utilisée pour faire des prédictions ? Par exemple, si l'amplitude d'une onde électronique est donnée par une fonction de position et de temps\(\Psi \, (x,t)\), définie pour tout x, où se trouve exactement l'électron ? Le but de ce chapitre est de répondre à ces questions.
Utilisation de la fonction Wave
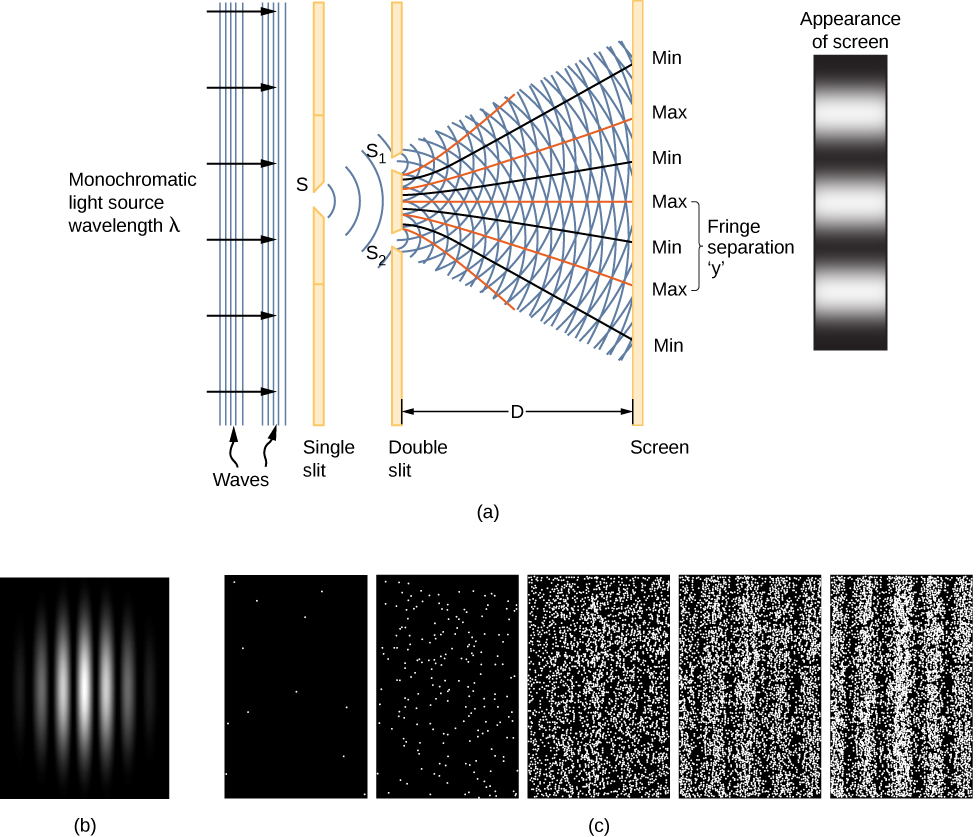
Un indice de la signification physique de la fonction d'onde\(\Psi \, (x,t)\) est fourni par l'interférence à deux fentes de la lumière monochromatique (Figure\(\PageIndex{1}\)) qui se comporte comme des ondes électromagnétiques. La fonction d'onde d'une onde lumineuse est donnée par E (x, t), et sa densité énergétique est donnée par\(|E|^2\), où E est l'intensité du champ électrique. L'énergie d'un photon individuel dépend uniquement de la fréquence de la lumière et\(|E|^2\) est donc proportionnelle au nombre de photons.\(\epsilon_{photon} = hf\) Lorsque des ondes lumineuses\(S_1\) interfèrent avec des ondes lumineuses provenant de l'écran de visualisation (\(S_2\)à une distance D), un motif d'interférence est produit (\(\PageIndex{1a}\)). Les franges claires correspondent à des points d'interférence constructive des ondes lumineuses, et les franges sombres correspondent à des points d'interférence destructrice des ondes lumineuses (\(\PageIndex{1b}\)).
Supposons que l'écran ne soit initialement pas exposé à la lumière. Si l'écran est exposé à une lumière très faible, le schéma d'interférence apparaît progressivement (Figure\(\PageIndex{1c}\), de gauche à droite). Les impacts de photons individuels sur l'écran apparaissent sous forme de points. La densité de points devrait être importante aux endroits où le schéma d'interférence sera finalement le plus intense. En d'autres termes, la probabilité (par unité de surface) qu'un photon touche un point particulier de l'écran est proportionnelle au carré du champ électrique total,\(|E|^2\) à ce point. Dans de bonnes conditions, le même schéma d'interférence se développe pour les particules de matière, telles que les électrons.
Consultez cette simulation interactive pour en savoir plus sur l'interférence des ondes quantiques.
Le carré de l'onde de matière\(|\Psi|^2\) dans une dimension a une interprétation similaire à celle du carré du champ électrique\(|E|^2\). Il donne la probabilité qu'une particule soit trouvée à une position et à un moment particuliers par unité de longueur, également appelée densité de probabilité. La probabilité (\(P\)) qu'une particule soit trouvée dans un intervalle étroit (x, x + dx) au temps t est donc
\[P(x,x + dx) = |\Psi \, (x,t)|^2 dx. \label{7.1} \]
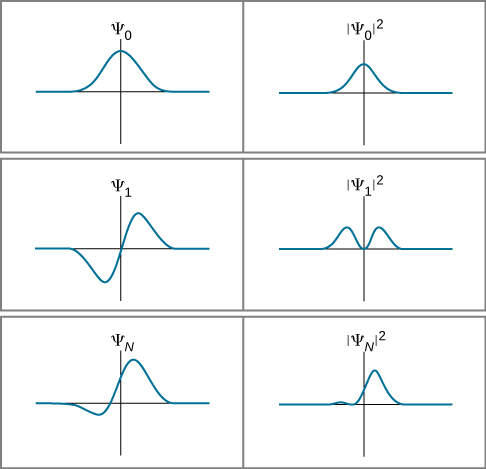
(Plus tard, nous définirons la magnitude au carré pour le cas général d'une fonction avec des « parties imaginaires ».) Cette interprétation probabiliste de la fonction d'onde est appelée interprétation de Born. Des exemples de fonctions d'onde et de leurs carrés pour un temps donné\(t\) sont donnés dans la figure\(\PageIndex{2}\).
Si la fonction d'onde varie lentement au cours de l'intervalle\(\Delta x\), la probabilité qu'une particule soit trouvée dans l'intervalle est d'environ
\[P(x,x + \Delta x) \approx |\Psi \, (x,t)|^2 \delta x. \label{7.2} \]
Notez que la mise au carré de la fonction d'onde garantit que la probabilité est positive. (Ceci est analogue à la mise au carré de l'intensité du champ électrique, qui peut être positive ou négative, pour obtenir une valeur d'intensité positive.) Toutefois, si la fonction d'onde ne varie pas lentement, il faut intégrer :
\[P(x,x + \Delta x) = \int_x^{x + \Delta x} |\Psi \, (x,t)|^2 dx. \label{7.3} \]
Cette probabilité est simplement la zone située sous la fonction\(|Ψ(x,t)|^2\) entre\(x\) et\(x+Δx\). La probabilité de trouver la particule « quelque part » (condition de normalisation) est
\[P(-\infty, +\infty) = \int_{-\infty}^{\infty} |\Psi \, (x,t)|^2 dx = 1.\label{7.4} \]
Pour une particule en deux dimensions, l'intégration se fait sur une surface et nécessite une double intégrale ; pour une particule en trois dimensions, l'intégration se fait sur un volume et nécessite une triple intégrale. Pour l'instant, nous nous en tenons au cas unidimensionnel simple.
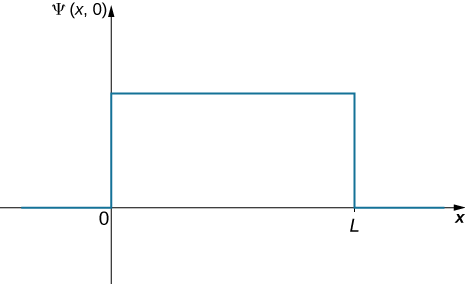
Une balle est contrainte de se déplacer le long d'une ligne à l'intérieur d'un tube de longueur\(L\). La balle est également susceptible de se trouver n'importe où dans le tube à un moment donné\(t\). Quelle est la probabilité de trouver la balle dans la moitié gauche du tube à ce moment-là ? (La réponse est 50 %, bien sûr, mais comment obtenir cette réponse en utilisant l'interprétation probabiliste de la fonction d'onde mécanique quantique ?)
Stratégie
La première étape consiste à noter la fonction d'onde. La balle se trouve également n'importe où dans la boîte, donc une façon de décrire la balle avec une fonction d'onde constante (Figure\(\PageIndex{3}\)). La condition de normalisation peut être utilisée pour trouver la valeur de la fonction et une simple intégration sur la moitié de la boîte donne la réponse finale.
Solution
The wavefunction of the ball can be written as \(\Psi \, (x,t) = C(0 < x < L)\), where \(C\) is a constant, and \(\Psi \, (x,t) = 0\) otherwise. We can determine the constant C by applying the normalization condition (we set \(t = 0\) to simplify the notation):
\[P(\infty, +\infty) = \int_{-\infty}^{\infty} |C|^2 dx = 1. \nonumber \]
This integral can be broken into three parts: (1) negative infinity to zero, (2) zero to L, and (3) L to infinity. The particle is constrained to be in the tube, so \(C=0\) outside the tube and the first and last integrations are zero. The above equation can therefore be written
\[P(x = 0, L) = \int_0^L |C|^2 dx = 1. \nonumber \]
The value C does not depend on x and can be taken out of the integral, so we obtain
\[|C|^2 \int_0^L dx = 1. \nonumber \]
Integration gives
\[C = \sqrt{\dfrac{1}{L}}. \nonumber \]
To determine the probability of finding the ball in the first half of the box (\(0 < x < L\)), we have
\[\begin{align} P(x = 0, L/2) &= \int_0^{L/2} \left|\sqrt{\dfrac{1}{L}}\right|^2dx \nonumber \\[5pt] &= \left(\dfrac{1}{L}\right)\dfrac{L}{2} \nonumber \\[5pt] &= 0.50. \end{align} \nonumber \]
Significance
The probability of finding the ball in the first half of the tube is 50%, as expected. Two observations are noteworthy. First, this result corresponds to the area under the constant function from \(x=0\) to \(L/2\) (the area of a square left of L/2). Second, this calculation requires an integration of the square of the wavefunction. A common mistake in performing such calculations is to forget to square the wavefunction before integration.
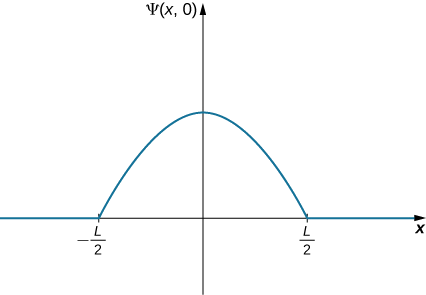
A ball is again constrained to move along a line inside a tube of length L. This time, the ball is found preferentially in the middle of the tube. One way to represent its wavefunction is with a simple cosine function (Figure \(\PageIndex{4}\)). What is the probability of finding the ball in the last one-quarter of the tube?
Stratégie
Nous utilisons la même stratégie qu'auparavant. Dans ce cas, la fonction d'onde possède deux constantes inconnues : l'une est associée à la longueur d'onde de l'onde et l'autre à l'amplitude de l'onde. Nous déterminons l'amplitude en utilisant les conditions limites du problème et nous évaluons la longueur d'onde en utilisant la condition de normalisation. L'intégration du carré de la fonction d'onde sur le dernier quart du tube donne la réponse finale. Le calcul est simplifié en centrant notre système de coordonnées sur le pic de la fonction d'onde.
Solution
La fonction d'onde de la balle peut être écrite
\[\Psi \, (x,t) = A \, \cos \, (kx) (-L/2 < x < L/2), \nonumber \]
où\(A\) est l'amplitude de la fonction d'onde et\(k = 2\pi/\lambda\) son numéro d'onde. Au-delà de cet intervalle, l'amplitude de la fonction d'onde est nulle car la bille est confinée dans le tube. Exiger que la fonction d'onde se termine à l'extrémité droite du tube donne
\[\Psi \left(x = \dfrac{L}{2}, 0 \right) = 0. \nonumber \]
Évaluer la fonction d'onde à des\(x = L/2\) données
\[A \, \cos \, (kL/2) = 0. \nonumber \]
Cette équation est satisfaite si l'argument du cosinus est un multiple entier de\(π/2\),,\(3π/2\)\(5π/2\), et ainsi de suite. Dans ce cas, nous avons
\[\dfrac{kL}{2} = \dfrac{\pi}{2}, \nonumber \]ou\[k = \dfrac{\pi}{L}. \nonumber \]
L'application de la condition de normalisation donne\(A = \sqrt{2/L}\), de sorte que la fonction d'onde de la balle est
\[\Psi \, (x,0) = \sqrt{\dfrac{2}{L}} \, cos \, (\pi x/L), \, -L/2 < x < L/2. \nonumber \]
Pour déterminer la probabilité de trouver la balle dans le dernier quart du tube, nous quadrillons la fonction et intégrons :
\[P(x = L/4, L/2) = \int_{L/4}^{L/2} \left|\sqrt{\dfrac{2}{L}} \, \cos \, \left(\dfrac{\pi x}{L}\right) \right| ^2 dx = 0.091. \nonumber \]
L'importance
La probabilité de trouver la balle dans le dernier quart du tube est de 9,1%. La balle a une longueur d'onde définie (\(\lambda = 2L\)). Si le tube est de longueur macroscopique (\(L = 1 \, m\)), l'impulsion de la balle est
\[p = \dfrac{h}{\lambda} = \dfrac{h}{2L} \approx10^{-36} m/s. \nonumber \]
Cet élan est bien trop faible pour être mesuré par un instrument humain.
Une interprétation de la fonction d'onde
Nous sommes maintenant en mesure de commencer à répondre aux questions posées au début de cette section. Tout d'abord, pour une particule itinérante décrite par\(\Psi \, (x,t) = A \, \sin \, (kx - \omega t)\), qu'est-ce que « onduler » ? Sur la base de la discussion ci-dessus, la réponse est une fonction mathématique qui peut, entre autres, être utilisée pour déterminer où la particule est susceptible de se trouver lorsqu'une mesure de position est effectuée. Ensuite, comment la fonction d'onde est-elle utilisée pour faire des prédictions ? S'il est nécessaire de déterminer la probabilité qu'une particule soit trouvée dans un certain intervalle, mettez la fonction d'onde au carré et intégrez-la sur l'intervalle d'intérêt. Bientôt, vous apprendrez bientôt que la fonction d'onde peut également être utilisée pour effectuer de nombreux autres types de prédictions.
Troisièmement, si une onde de matière est donnée par la fonction d'onde\(\Psi \, (x,t)\), où se trouve exactement la particule ? Deux réponses existent : (1) lorsque l'observateur ne regarde pas (ou que la particule n'est pas détectée autrement), la particule est partout (\(x = -\infty, +\infty\)) ; et (2) lorsque l'observateur regarde (la particule est détectée), la particule « saute » dans un état de position particulier (\(x,x + dx\) ) avec une probabilité donnée par
\[P(x,x + dx) = |\Psi \, (x,t)|^2 dx \nonumber \]
via un processus appelé réduction d'état ou effondrement de la fonction d'onde. Cette réponse s'appelle l'interprétation de Copenhague de la fonction d'onde, ou de la mécanique quantique.
Pour illustrer cette interprétation, considérez le cas simple d'une particule qui peut occuper un petit contenant à\(x_1\) ou\(x_2\) (Figure\(\PageIndex{5}\)). En physique classique, nous supposons que la particule est située soit là où l'observateur ne regarde pas,\(x_1\) soit\(x_2\) lorsque celui-ci ne le regarde pas. Cependant, en mécanique quantique, la particule peut exister dans un état de position indéfini, c'est-à-dire qu'elle peut être localisée à l'endroit\(x_1\) et au\(x_2\) moment où l'observateur ne regarde pas. L'hypothèse selon laquelle une particule ne peut avoir qu'une seule valeur de position (lorsque l'observateur ne regarde pas) est abandonnée. Des commentaires similaires peuvent être faits sur d'autres grandeurs mesurables, telles que la dynamique et l'énergie.
The bizarre consequences of the Copenhagen interpretation of quantum mechanics are illustrated by a creative thought experiment first articulated by Erwin Schrödinger (National Geographic, 2013) (\(\PageIndex{6}\)):
“A cat is placed in a steel box along with a Geiger counter, a vial of poison, a hammer, and a radioactive substance. When the radioactive substance decays, the Geiger detects it and triggers the hammer to release the poison, which subsequently kills the cat. The radioactive decay is a random [probabilistic] process, and there is no way to predict when it will happen. Physicists say the atom exists in a state known as a superposition—both decayed and not decayed at the same time. Until the box is opened, an observer doesn’t know whether the cat is alive or dead—because the cat’s fate is intrinsically tied to whether or not the atom has decayed and the cat would [according to the Copenhagen interpretation] be “living and dead ... in equal parts” until it is observed.”
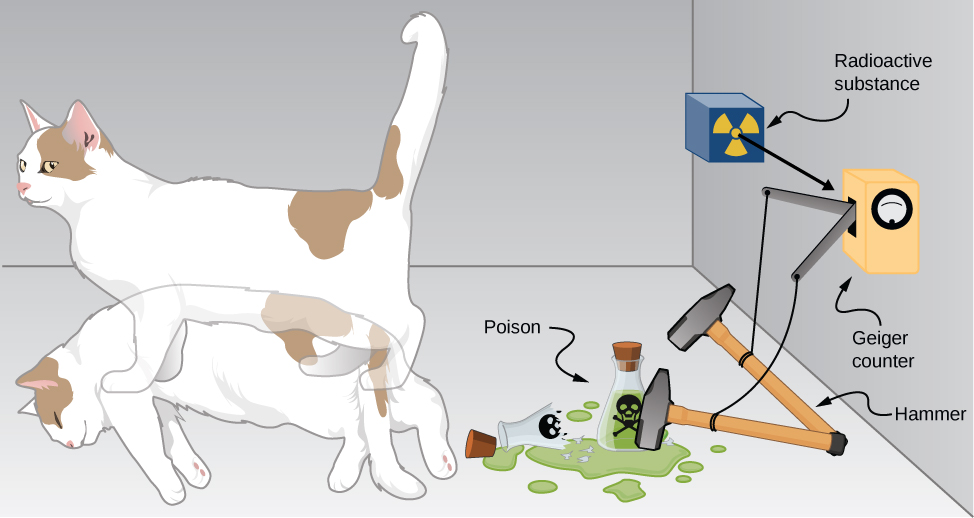
Schrödinger took the absurd implications of this thought experiment (a cat simultaneously dead and alive) as an argument against the Copenhagen interpretation. However, this interpretation remains the most commonly taught view of quantum mechanics.
Two-state systems (left and right, atom decays and does not decay, and so on) are often used to illustrate the principles of quantum mechanics. These systems find many applications in nature, including electron spin and mixed states of particles, atoms, and even molecules. Two-state systems are also finding application in the quantum computer, as mentioned in the introduction of this chapter. Unlike a digital computer, which encodes information in binary digits (zeroes and ones), a quantum computer stores and manipulates data in the form of quantum bits, or qubits. In general, a qubit is not in a state of zero or one, but rather in a mixed state of zero and one. If a large number of qubits are placed in the same quantum state, the measurement of an individual qubit would produce a zero with a probability p, and a one with a probability \(q = 1 - p\). Some scientists believe that quantum computers are the future of the computer industry.
Complex Conjugates
Later in this section, you will see how to use the wavefunction to describe particles that are “free” or bound by forces to other particles. The specific form of the wavefunction depends on the details of the physical system. A peculiarity of quantum theory is that these functions are usually complex functions. A complex function is one that contains one or more imaginary numbers (\(i = \sqrt{-1}\)). Experimental measurements produce real (nonimaginary) numbers only, so the above procedure to use the wavefunction must be slightly modified. In general, the probability that a particle is found in the narrow interval \((x, x + dx)\) at time \(t\) is given by
\[P (x,x + dx) = |\Psi \, (x,t)|^2 dx = \Psi^* (x,t) \, \Psi \, (x,t) \, dx, \label{7.5} \]
where \(\Psi^* (x,t)\) is the complex conjugate of the wavefunction. The complex conjugate of a function is obtaining by replacing every occurrence of \(i = \sqrt{-1}\) in that function with \(-i\). This procedure eliminates complex numbers in all predictions because the product \(\Psi^* (x,t) \, \Psi \, (x,t)\) is always a real number.
If \(a = 3 + 4i\), what is the product \(a^*a\)?
- Answer
-
\[(3 + 4i)(3 - 4i) = 9 - 16i^2 = 25 \nonumber \]
Consider the motion of a free particle that moves along the x-direction. As the name suggests, a free particle experiences no forces and so moves with a constant velocity. As we will see in a later section of this chapter, a formal quantum mechanical treatment of a free particle indicates that its wavefunction has real and complex parts. In particular, the wavefunction is given by
\[\Psi \, (x,t) = A \, \cos \, (kx - \omega t) + i A \, \sin \, (kx - \omega t), \label{eq56} \]
where \(A\) is the amplitude, \(k\) is the wave number, and \(ω\) is the angular frequency. Euler’s formula
\[\underbrace{e^{i\phi} = \cos \, (\phi) + i \, \sin \, (\phi)}_{\text{Euler’s formula}} \nonumber \]
can be used to rewrite Equation \ref{eq56} in the form
\[\Psi \, (x,t) = Ae^{i(kx - \omega t)} = Ae^{i\phi}, \nonumber \]
where \(\phi\) is the phase angle. If the wavefunction varies slowly over the interval \(\Delta x\), the probability of finding the particle in that interval is
\[P (x,x + \Delta x) \approx \Psi^* (x,t) \, \Psi \, (x,t) \, \Delta x = (Ae^{i\phi})(A^* e^{-i\phi}) \, \Delta x = (A^*A) \Delta x. \nonumber \]
If \(A\) has real and complex parts (\(a+ib\), where \(a\) and \(b\) are real constants), then
\[A^*A = (a + ib)(a - ib) = a^2 + b^2. \nonumber \]
Notice that the complex numbers have vanished. Thus,
\[P(x,x + \Delta x) \approx |A|^2 \delta x \nonumber \]
is a real quantity. The interpretation of \(\Psi^* (x,t) \, \Psi \, (x,t)\) as a probability density ensures that the predictions of quantum mechanics can be checked in the “real world.”
Suppose that a particle with energy E is moving along the x-axis and is confined in the region between 0 and L. One possible wavefunction is
\[\psi (x,t) =\begin{cases}
Ae^{-iEt/\hbar} \sin \, \dfrac{\pi x}{L} & 0 \leq x \leq L \\
0 & x < 0 \text{ and } x > L \end{cases} \nonumber \]
Determine the normalization constant.
- Answer
-
\(A = \sqrt{2/L}\)
Expectation Values
In classical mechanics, the solution to an equation of motion is a function of a measurable quantity, such as \(x(t)\), where \(x\) is the position and \(t\) is the time. Note that the particle has one value of position for any time \(t\). In quantum mechanics, however, the solution to an equation of motion is a wavefunction, \(\Psi \, (x,t)\). The particle has many values of position for any time \(t\), and only the probability density of finding the particle, \(|\Psi \, (x,t)|^2\), can be known. The average value of position for a large number of particles with the same wavefunction is expected to be
\[\langle x \rangle = \int_{-\infty}^{\infty} xP(x,t) \, dx = \int_{-\infty}^{\infty} x \Psi^* (x,t) \, \Psi \, (x,t) \, dx. \label{7.6} \]
This is called the expectation value of the position. It is usually written
\[\langle x \rangle = \int_{-\infty}^{\infty} \Psi^* (x,t) \, x \Psi \, (x,t) \, dx. \label{7.7} \]
where the \(x\) is sandwiched between the wavefunctions. The reason for this will become apparent soon. Formally, \(x\) is called the position operator.
At this point, it is important to stress that a wavefunction can be written in terms of other quantities as well, such as velocity (\(v\)), momentum (\(p\)), and kinetic energy (\(K\)). The expectation value of momentum, for example, can be written
\[\langle p \rangle = \int_{-\infty}^{\infty} \Psi^* (p,t) \, p\Psi \, (p,t) \, dp, \label{7.8} \]
where \(dp\) is used instead of \(dx\) to indicate an infinitesimal interval in momentum. In some cases, we know the wavefunction in position, \(\Psi \, (x,t)\), but seek the expectation of momentum. The procedure for doing this is
\[\langle p \rangle = \int_{-\infty}^{\infty} \Psi^* (x,t) \, \left(-i\hbar \dfrac{d}{dx}\right) \, \Psi \, (x,t) \, dx, \label{7.9} \]
where the quantity in parentheses, sandwiched between the wavefunctions, is called the momentum operator in the x-direction. [The momentum operator in Equation \ref{7.9} is said to be the position-space representation of the momentum operator.] The momentum operator must act (operate) on the wavefunction to the right, and then the result must be multiplied by the complex conjugate of the wavefunction on the left, before integration. The momentum operator in the x-direction is sometimes denoted
\[\langle p \rangle = - i\hbar \dfrac{d}{dx},\label{7.10} \]
Momentum operators for the y- and z-directions are defined similarly. This operator and many others are derived in a more advanced course in modern physics. In some cases, this derivation is relatively simple. For example, the kinetic energy operator is just
\[\begin{align} (K)_{op} &= \dfrac{1}{2}m(v_x)_{op}^2 \\[5pt] &= \dfrac{(p_x)^2_{op}}{2m} \\[5pt] &= \dfrac {\left(-i\hbar \dfrac{d}{dx}\right)^2}{2m} \\[5pt] &= \dfrac{-\hbar^2}{2m} \left(\dfrac{d}{dx}\right)\left(\dfrac{d}{dx}\right).\label{7.11} \end{align} \]
Thus, if we seek an expectation value of kinetic energy of a particle in one dimension, two successive ordinary derivatives of the wavefunction are required before integration.
Expectation-value calculations are often simplified by exploiting the symmetry of wavefunctions. Symmetric wavefunctions can be even or odd. An even function is a function that satisfies
\[\psi(x) = \psi(-x). \label{7.12} \]
In contrast, an odd function is a function that satisfies
\[\psi(x) = -\psi(-x).\label{7.13} \]
An example of even and odd functions is shown in Figure \(\PageIndex{7}\). An even function is symmetric about the y-axis. This function is produced by reflecting \(\psi (x)\) for \(x > 0\) about the vertical y-axis. By comparison, an odd function is generated by reflecting the function about the y-axis and then about the x-axis. (An odd function is also referred to as an anti-symmetric function.)
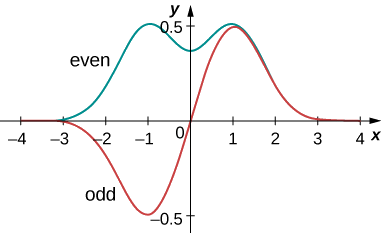
En général, une fonction paire multipliée par une fonction paire produit une fonction paire. Un exemple simple de fonction uniforme est le produit\(x^2e^{-x^2}\) (même temps pair est pair). De même, une fonction impaire multipliée par une fonction impaire produit une fonction paire, telle que x sin x (les fois impairs sont pairs). Cependant, une fonction impaire multipliée par une fonction paire produit une fonction impaire, telle que\(x^2e^{-x^2}\) (un nombre impair est impair). L'intégrale sur tout l'espace d'une fonction impaire est nulle, car l'aire totale de la fonction au-dessus de l'axe x annule la zone (négative) située en dessous. Comme le montre l'exemple suivant, cette propriété des fonctions impaires est très utile.
La fonction d'onde normalisée d'une particule est
\[\psi(x) = e^{-|x|/x_0} /\sqrt{x_0}. \nonumber \]
Déterminez la valeur attendue de la position.
Stratégie
Remplacez la fonction d'onde par l'équation \ ref {7.7} et évaluez. L'opérateur de position introduit un facteur multiplicatif uniquement, de sorte que l'opérateur de position n'a pas besoin d'être « pris en sandwich ».
Solution
Multipliez d'abord, puis intégrez :
\[\begin{align*} \langle x \rangle &= \int_{-\infty}^{\infty} dx\,x|\psi(x)|^2 \nonumber \\[4pt] &= \int_{-\infty}^{\infty} dx\, x|\dfrac{e^{-|x|/x_0}}{\sqrt{x_0}}|^2 \nonumber \\[4pt] &= \dfrac{1}{x_0} \int_{-\infty}^{\infty} dx\, xe^{-2|x|/x_0} \nonumber \\[4pt] &= 0. \nonumber \end{align*} \nonumber \]
L'importance
La fonction de l'integrand (\(xe^{-2|x|/x_0}\)) est impaire puisqu'elle est le produit d'une fonction impaire (x) et d'une fonction paire (\(e^{-2|x|/x_0}\)). L'intégrale disparaît car la surface totale de la fonction autour de l'axe x annule la zone (négative) située en dessous. Le résultat (\(\langle x \rangle = 0\)) n'est pas surprenant puisque la fonction de densité de probabilité est symétrique\(x = 0\).
La fonction d'onde dépendante du temps d'une particule confinée dans une région comprise entre 0 et L est
\[\psi(x,t) = A \, e^{-i\omega t} \sin \, (\pi x/L) \nonumber \]
où\(\omega\) est la fréquence angulaire et\(E\) l'énergie de la particule. (Remarque : La fonction varie en tant que sinus en raison des limites (0 à L). Lorsque\(x = 0\), le facteur sinusoïdal est nul et que la fonction d'onde est nulle, conformément aux conditions limites.) Calculez les valeurs attendues de position, de moment et d'énergie cinétique.
Stratégie
Nous devons d'abord normaliser la fonction d'onde pour trouver A. Ensuite, nous utilisons les opérateurs pour calculer les valeurs attendues.
Solution
Calcul de la constante de normalisation :
\[\begin{align*} 1 &= \int_0^L dx\, \psi^* (x) \psi(x) \nonumber \\[4pt] &= \int_0^L dx \, \left(A e^{+i\omega t} \sin \, \dfrac{\pi x}{L}\right) \left(A e^{-i\omega t} \sin \, \dfrac{\pi x}{L}\right) \nonumber \\[4pt] &= A^2 \int_0^L dx \, \sin^2 \, \dfrac{\pi x}{L} \nonumber \\[4pt] &= A^2 \dfrac{L}{2} \nonumber \\[4pt] \Rightarrow A &= \sqrt{\dfrac{2}{L}}. \nonumber \end{align*} \nonumber \]
La valeur attendue de la position est
\[\begin{align*}\langle x \rangle &= \int_0^L dx \, \psi^* (x) x \psi(x) \nonumber \\[4pt] &= \int_0^L dx \, \left(A e^{+i\omega t} \sin \, \dfrac{\pi x}{L}\right) x \left(A e^{-i\omega t} \sin \, \dfrac{\pi x}{L}\right) \nonumber \\[4pt] &= A^2 \int_0^L dx\,x \, \sin^2 \, \dfrac{\pi x}{L} \nonumber \\[4pt] &= A^2 \dfrac{L^2}{4} \nonumber \\[4pt] \Rightarrow A &= \dfrac{L}{2}. \nonumber \end{align*} \nonumber \]
La valeur attendue de l'impulsion dans la direction x nécessite également une intégrale. Pour configurer cette intégrale, l'opérateur associé doit, en règle générale, agir à droite sur la fonction d'onde\(\psi(x)\) :
\[\begin{align*} -i\hbar\dfrac{d}{dx} \psi(x) &= -i\hbar \dfrac{d}{dx} Ae^{-i\omega t}\sin \, \dfrac{\pi x}{L} \nonumber \\[4pt] &= - i\dfrac{Ah}{2L} e^{-i\omega t} \cos\, \dfrac{\pi x}{L}. \nonumber \end{align*} \nonumber \]
Par conséquent, la valeur attendue de la dynamique est
\[ \begin{align*} \langle p \rangle &= \int_0^L dx \left(Ae^{+i\omega t}sin \dfrac{\pi x}{L}\right)\left(-i \dfrac{Ah}{2L} e^{-i\omega t} cos \, \dfrac{\pi x}{L}\right) \nonumber \\[4pt] &= -i \dfrac{A^2h}{4L} \int_0^L dx \, \sin \, \dfrac{2\pi x}{L} \nonumber \\[4pt] &= 0. \nonumber \end{align*} \nonumber \]
La fonction dans l'intégrale est une fonction sinusoïdale dont la longueur d'onde est égale à la largeur du puits, L, une fonction étrange d'environ\(x = L/2\). En conséquence, l'intégrale disparaît.
La valeur attendue de l'énergie cinétique dans la direction x nécessite que l'opérateur associé agisse sur la fonction d'onde :
\[ \begin{align} -\dfrac{\hbar^2}{2m}\dfrac{d^2}{dx^2} \psi (x) &= - \dfrac{\hbar^2}{2m} \dfrac{d^2}{dx^2} Ae^{-i\omega t} \, \sin \, \dfrac{\pi x}{L} \nonumber \\[4pt] &= - \dfrac{\hbar^2}{2m} Ae^{-i\omega t} \dfrac{d^2}{dx^2} \, \sin \, \dfrac{\pi x}{L} \nonumber \\[4pt] &= \dfrac{Ah^2}{8mL^2} e^{-i\omega t} \, \sin \, \dfrac{\pi x}{L}. \nonumber \end{align} \nonumber \]
Ainsi, la valeur attendue de l'énergie cinétique est
\[\begin{align*} \langle K \rangle &= \int_0^L dx \left( Ae^{+i\omega t} \, \sin \, \dfrac{\pi x}{L}\right) \left(\dfrac{Ah^2}{8mL^2} e^{-i\omega t} \, \sin \, \dfrac{\pi x}{L}\right) \nonumber \\[4pt] &= \dfrac{A^2h^2}{8mL^2} \int_0^L dx \, \sin^2 \, \dfrac{\pi x}{L} \nonumber \\[4pt] &= \dfrac{A^2h^2}{8mL^2} \dfrac{L}{2} \nonumber \\[4pt] &= \dfrac{h^2}{8mL^2}. \end{align*} \nonumber \]
L'importance
La position moyenne d'un grand nombre de particules dans cet état est de\(L/2\). La quantité de mouvement moyenne de ces particules est nulle car une particule donnée est également susceptible de se déplacer vers la droite ou vers la gauche. Cependant, la particule n'est pas au repos car son énergie cinétique moyenne n'est pas nulle. Enfin, la densité de probabilité est
\[|\psi|^2 = (2/L) \, \sin^2 (\pi x/L). \nonumber \]
Cette densité de probabilité est maximale à l'emplacement\(L/2\) et est nulle à\(x = 0\) et à\(x = L\). Notez que ces conclusions ne dépendent pas explicitement du temps.
Pour la particule de l'exemple ci-dessus, déterminez la probabilité de la localiser entre les positions\(0\) et\(L/4\).
- Réponse
-
\((1/2 - 1/\pi) /2 = 9\%\)
La mécanique quantique fait de nombreuses prévisions surprenantes. Cependant, en 1920, Niels Bohr (fondateur de l'Institut Niels Bohr de Copenhague, d'où provient le terme « interprétation de Copenhague ») a affirmé que les prédictions de la mécanique quantique et de la mécanique classique devaient concorder pour tous les systèmes macroscopiques, tels que les planètes en orbite, les balles rebondissantes, les chaises à bascule et ressorts. Ce principe de correspondance est désormais généralement accepté. Il suggère que les règles de la mécanique classique sont une approximation des règles de la mécanique quantique pour les systèmes à très grandes énergies. La mécanique quantique décrit à la fois le monde microscopique et le monde macroscopique, mais la mécanique classique ne décrit que ce dernier.


