4.5 : Réseaux de diffraction

Objectifs d'apprentissage

À la fin de cette section, vous serez en mesure de :

• Discutez du motif obtenu à partir des réseaux de diffraction
• Expliquer les effets des réseaux de diffraction

L'analyse de l'interférence de la lumière traversant deux fentes présente le cadre théorique de l'interférence et nous donne un aperçu historique des expériences de Thomas Young. Cependant, la plupart des applications modernes d'interférence de fentes utilisent non seulement deux fentes, mais de nombreuses fentes, proches de l'infini à des fins pratiques. L'élément optique clé est appelé réseau de diffraction, un outil important dans l'analyse optique.

Réseaux de diffraction : un nombre infini de fentes

L'analyse de l'interférence à fentes multiples dans Interference nous permet de considérer ce qui se passe lorsque le nombre de fentes N approche de l'infini. Rappelez-vous que des maxima\(N - 2\) secondaires apparaissent entre les maxima principaux. Nous pouvons voir qu'un nombre infini de maxima secondaires apparaîtront et qu'un nombre infini de franges sombres les sépareront. Cela rend l'espacement entre les franges, et donc la largeur des maxima, infiniment petit. De plus, comme l'intensité des maxima secondaires est proportionnelle à\(1/N^2\), elle se rapproche de zéro, de sorte que les maxima secondaires ne sont plus visibles. Il ne reste que les maxima principaux, désormais très clairs et très étroits (Figure\(\PageIndex{1}\)).

Figure\(\PageIndex{1}\) : (a) Intensité de la lumière transmise par un grand nombre de fentes. Lorsque N s'approche de l'infini, seuls les maxima principaux restent sous forme de lignes très claires et très étroites. (b) Un faisceau laser a traversé un réseau de diffraction. (crédit b : modification d'une œuvre de Sebastian Stapelberg)

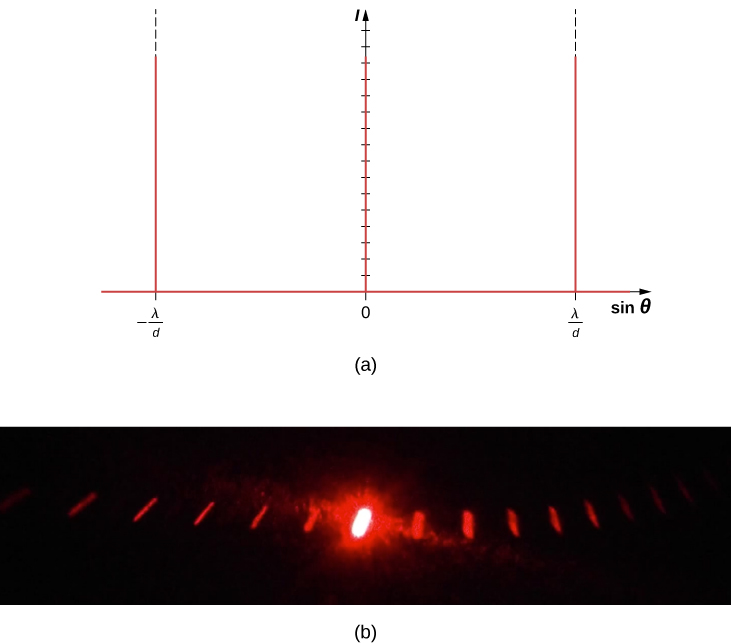
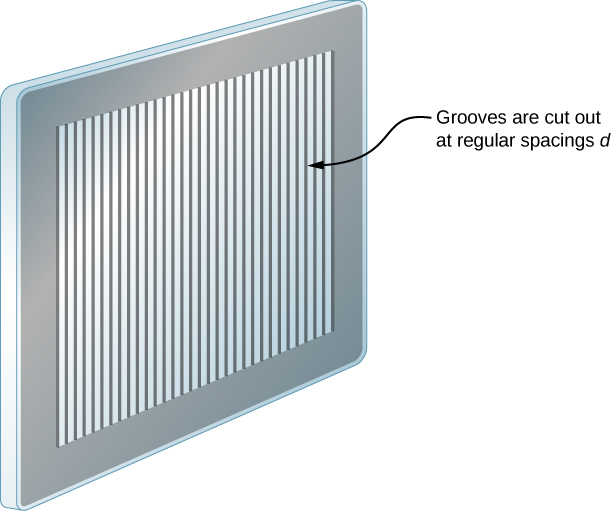
En réalité, le nombre de fentes n'est pas infini, mais il peut être très important, suffisamment grand pour produire l'effet équivalent. Un élément optique appelé réseau de diffraction en est un excellent exemple. Un réseau de diffraction peut être fabriqué en sculptant du verre à l'aide d'un outil tranchant en un grand nombre de lignes parallèles positionnées avec précision, les zones intactes agissant comme des fentes (Figure\(\PageIndex{2}\)). Ce type de caillebotis peut être produit photographiquement en série à moindre coût. Comme il peut y avoir plus de 1 000 lignes par millimètre à travers le réseau, lorsqu'une section de quelques millimètres seulement est éclairée par un rayon entrant, le nombre de fentes illuminées est effectivement infini, ce qui permet d'obtenir des maxima principaux très nets.

Figure\(\PageIndex{2}\) : Un réseau de diffraction peut être fabriqué en sculptant du verre à l'aide d'un outil tranchant selon un grand nombre de lignes parallèles positionnées avec précision.

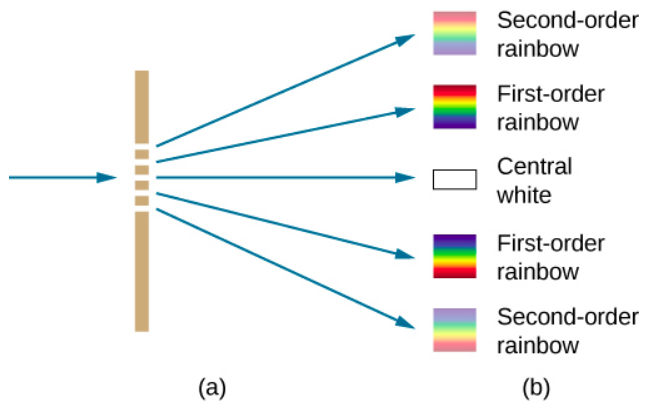
Les réseaux de diffraction fonctionnent à la fois pour la transmission de la lumière, comme sur la figure\(\PageIndex{3}\), et pour la réflexion de la lumière, comme sur les ailes des papillons et l'opale australienne sur la figure\(\PageIndex{4a}\). Des réseaux de diffraction naturels apparaissent également dans les plumes de certains oiseaux tels que le colibri. De minuscules structures semblables à des doigts aux motifs réguliers agissent comme des réseaux de réflexion, produisant des interférences constructives qui donnent des couleurs aux plumes non seulement en raison de leur pigmentation. C'est ce qu'on appelle l'iridescence.

Figure\(\PageIndex{3}\) : (a) La lumière traversant un réseau de diffraction est diffractée selon un motif similaire à une double fente, avec des zones claires à différents angles. (b) Le motif obtenu pour la lumière blanche incidente sur un réseau. Le maximum central est le blanc, et les maxima d'ordre supérieur dispersent la lumière blanche dans un arc-en-ciel de couleurs.

Figure\(\PageIndex{4}\) : (a) Cette opale australienne et (b) les ailes de papillon possèdent des rangées de réflecteurs qui agissent comme des réseaux de réflexion, reflétant différentes couleurs sous différents angles. (crédit a : modification de l'œuvre par « Opals-On-Black » /Flickr ; crédit b : modification de l'œuvre par « whologwhy » /Flickr)

Applications des réseaux de diffraction

Où sont utilisés les réseaux de diffraction dans les applications ? Les réseaux de diffraction sont couramment utilisés pour la dispersion spectroscopique et l'analyse de la lumière. Ce qui les rend particulièrement utiles, c'est qu'elles forment un motif plus net que les doubles fentes. C'est-à-dire que leurs franges lumineuses sont plus étroites et plus lumineuses tandis que leurs régions sombres sont plus sombres. Les réseaux de diffraction sont des composants clés des monochromateurs utilisés, par exemple, pour l'imagerie optique de longueurs d'onde particulières à partir d'échantillons biologiques ou médicaux. Un réseau de diffraction peut être choisi pour analyser spécifiquement une longueur d'onde émise par des molécules présentes dans des cellules malades dans un échantillon de biopsie ou pour aider à exciter des molécules stratégiques de l'échantillon avec une longueur d'onde de lumière sélectionnée. Une autre utilisation vitale concerne les technologies de fibres optiques, où les fibres sont conçues pour fournir des performances optimales à des longueurs d'onde spécifiques. Une gamme de réseaux de diffraction est disponible pour sélectionner les longueurs d'onde pour une telle utilisation.

Exemple\(\PageIndex{1}\): Calculating Typical Diffraction Grating Effects

Des réseaux de diffraction de 10 000 raies par centimètre sont facilement disponibles. Supposons que vous en ayez un et que vous envoyiez un faisceau de lumière blanche à travers celui-ci vers un écran situé à 2 mètres de distance.

1. Déterminez les angles de diffraction du premier ordre des longueurs d'onde les plus courtes et les plus longues de la lumière visible (380 et 760 nm, respectivement).
2. Quelle est la distance entre les extrémités de l'arc-en-ciel de lumière visible produite sur l'écran pour provoquer des interférences de premier ordre ? (Figurine\(\PageIndex{5}\)).

3. 

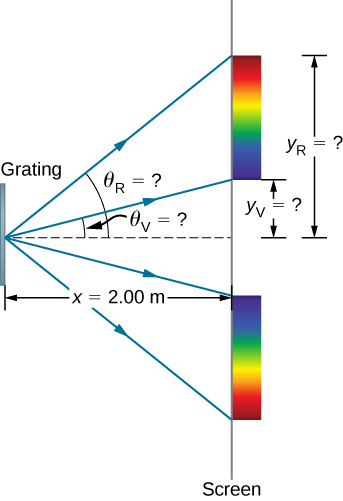
   Figure\(\PageIndex{5}\) : (a) Le réseau de diffraction considéré dans cet exemple produit un arc-en-ciel de couleurs sur un écran\(x = 2.00 \, m\) éloigné du réseau. Les distances le long de l'écran sont mesurées perpendiculairement à la direction X. En d'autres termes, le motif arc-en-ciel s'étend hors de la page.

(b) À vol d'oiseau, le motif arc-en-ciel est visible sur une table où l'équipement est placé.

Stratégie

Une fois qu'une valeur pour l'espacement des fentes du réseau de diffraction\(d\) a été déterminée, les angles des lignes nettes peuvent être déterminés à l'aide de l'équation

\[d \, \sin \, \theta = m\lambda \nonumber \]

pour\(m = 0, \pm1, \pm2, ... \).

Comme il y a 10 000 lignes par centimètre, chaque ligne est séparée par 1/10 000 de centimètre. Une fois que nous connaissons les angles, nous pouvons déterminer les distances le long de l'écran en utilisant une simple trigonométrie.

Solution

1. La distance entre les fentes est de\(d = (1 \, cm)/10,000 = 1.00 \times 10^{-4} \, cm\) ou\(1.00 \times 10^{-6} m\). Appelons les deux angles\(\theta_V\) pour le violet (380 nm) et\(\theta_R\) pour le rouge (760 nm). Résoudre l'équation\(d \, \sin \theta_V = m\lambda\) pour\(\sin \, \theta_V\),

   \[\sin \, \theta_V = \frac{m\lambda_V}{d},\nonumber \]

   où m = 1 pour le premier ordre et\(\lambda_V = 380 \, nm = 3.80 \times 10^{-7}m\). La substitution de ces valeurs donne

   \[\sin \, \theta_V = \frac{3.80 \times 10^{-7}m}{1.00 \times 10^{-6}m} = 0.380.\nonumber \]

   Ainsi, l'angle\(\theta_V\) est

   \[\theta_V = \sin^{-1} 0.380 = 22.33°.\nonumber \]

   De même,

   \[\sin \, \theta_R = \frac{7.60 \times 10^{-7}m}{1.00 \times 10^{-6}m} = 0.760.\nonumber \]

   Ainsi, l'angle\(\theta_R\) est

   \[\theta_R = \sin^{-1} 0.760 = 49.46°. \nonumber \]

   Notez que dans les deux équations, nous avons rapporté les résultats de ces calculs intermédiaires à quatre chiffres significatifs à utiliser avec le calcul de la partie (b).
2. Les distances affichées à l'écran sont étiquetées\(y_V\) et illustrées\(y_R\) dans la figure\(\PageIndex{5}\). Remarquez que\(tan \, \theta = y/x\). Nous pouvons résoudre pour\(y_V\) et\(y_R\). C'est-à-dire,

   \[y_V = x \, \tan \, \theta_V = (2.00 \, m)(\tan \, 22.33°) = 0.815 \, m \nonumber \]

   et

   \[y_R = x \, \tan \, \theta_R = (2.00 \, m)(\tan \, 49.46°) = 2.338 \, m. \nonumber \]

   La distance qui les sépare est donc

   \[y_R - y_V = 1.523 \, m \nonumber \]

L'importance

La grande distance entre les extrémités rouge et violette de l'arc-en-ciel produite par la lumière blanche indique le potentiel de ce réseau de diffraction en tant qu'outil spectroscopique. Plus il peut étaler les longueurs d'onde (plus grande dispersion), plus le spectre est détaillé. Cela dépend de la qualité du réseau de diffraction : il doit être réalisé avec une grande précision en plus de comporter des lignes rapprochées.

Exercice\(\PageIndex{1}\)

Si l'espacement entre les lignes d'un réseau de diffraction n'\(d\)est pas connu avec précision, nous pouvons utiliser une source de lumière dont la longueur d'onde est bien déterminée pour le mesurer. Supposons que la frange constructive du premier ordre de la raie d'\(H_{\beta}\)émission d'hydrogène (\(\lambda = 656.3 \, nm\)) soit mesurée à 11,36° à l'aide d'un spectromètre à réseau de diffraction. Quel est l'espacement entre les lignes de cette grille ?

Réponse

\(3.332 \times 10^{-6} m\)soit 300 lignes par millimètre

Prenez la même simulation que celle que nous avons utilisée pour la diffraction à double fente et essayez d'augmenter le nombre de fentes de\(N = 2\) à\(N = 3, 4, 5, ...\). Les pics primaires deviennent plus nets et les pics secondaires de moins en moins prononcés. Lorsque vous atteignez le nombre maximum de\(N = 20\), le système se comporte comme un réseau de diffraction.