4.4 : Diffraction à double fente
- Page ID
- 189628
À la fin de cette section, vous serez en mesure de :
- Décrire l'effet combiné de l'interférence et de la diffraction à l'aide de deux fentes, chacune ayant une largeur finie
- Déterminer les intensités relatives des franges d'interférence au sein d'un diagramme de diffraction
- Identifier les commandes manquantes, le cas échéant
Lorsque nous avons étudié l'interférence dans l'expérience à double fente de Young, nous avons ignoré l'effet de diffraction dans chaque fente. Nous avons supposé que les fentes étaient si étroites que sur l'écran, vous ne pouviez voir que l'interférence de la lumière provenant de deux sources ponctuelles. Si la fente est inférieure à la longueur d'onde, la Figure 4.3.4a montre qu'il n'y a qu'une diffusion de la lumière et qu'il n'y a pas de pics ni de creux sur l'écran. Il était donc raisonnable d'omettre l'effet de diffraction dans ce chapitre. Toutefois, si vous élargissez la fente, les figures 4.3.4b et (c) montrent que vous ne pouvez pas ignorer la diffraction. Dans cette section, nous étudions les complications de l'expérience à double fente qui surviennent lorsque vous devez également prendre en compte l'effet de diffraction de chaque fente.
Pour calculer le diagramme de diffraction pour deux fentes (ou n'importe quel nombre de), nous devons généraliser la méthode que nous venons d'utiliser pour une seule fente. C'est-à-dire qu'à travers chaque fente, nous plaçons une distribution uniforme de sources ponctuelles qui rayonnent des ondelettes de Huygens, puis nous additionnons les ondelettes de toutes les fentes. Cela donne l'intensité à n'importe quel point de l'écran. Bien que les détails de ce calcul puissent être compliqués, le résultat final est assez simple :
Motif de diffraction à deux fentes
Le diagramme de diffraction de deux fentes de largeur\(a\) séparées par une distance d est le diagramme d'interférence de deux sources ponctuelles séparées par d multiplié par le motif de diffraction d'une fente de largeur\(a\).
En d'autres termes, les emplacements des franges d'interférence sont donnés par l'équation
\[d \, \sin \, \theta = m \lambda \nonumber \]
comme lorsque nous considérions les fentes comme des sources ponctuelles, mais les intensités des franges sont maintenant réduites par des effets de diffraction, selon l'équation 4.3.11. [Notez que dans le chapitre sur les interférences, nous avons écrit\(d \, sin \, \theta = m \lambda\) et utilisé l'entier\(m\) pour faire référence aux franges d'interférence. L'équation 4.2.1 utilise également\(m\), mais cette fois pour faire référence aux minima de diffraction. Si les deux équations sont utilisées simultanément, il est recommandé d'utiliser une variable différente (telle que\(n\)) pour l'un de ces nombres entiers afin de les différencier.]
Les effets d'interférence et de diffraction agissent simultanément et produisent généralement des minima sous différents angles. Cela donne lieu à un schéma complexe sur l'écran, dans lequel certains des maxima d'interférence provenant des deux fentes sont absents si le maximum de l'interférence se situe dans la même direction que le minimum de la diffraction. Nous appelons un tel pic manquant un ordre manquant. Un exemple de diagramme de diffraction sur l'écran est illustré à la figure\(\PageIndex{1}\). La ligne continue avec de multiples pics de différentes hauteurs représente l'intensité observée sur l'écran. Il est le produit du diagramme d'interférence des ondes provenant de fentes séparées et de la diffraction des ondes provenant de l'intérieur d'une fente.
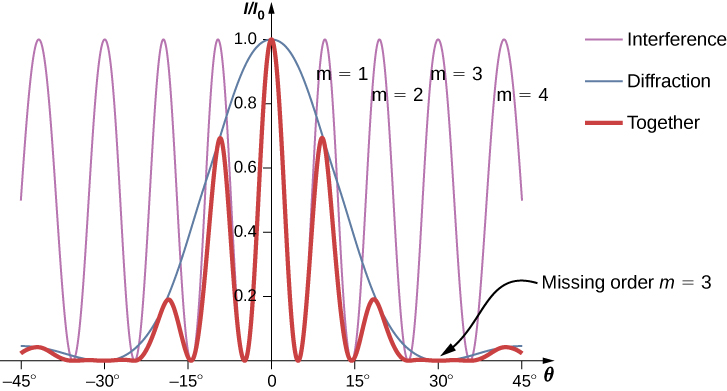
La figure\(\PageIndex{1}\) montre que l'intensité de la frange pour m=3 est nulle, mais qu'en est-il des autres franges ? Calculez l'intensité de la frange à m=1 par rapport à\(I_0\) l'intensité du pic central.
Stratégie
Déterminez l'angle de la frange d'interférence à double fente à l'aide de l'équation d'interférence, puis déterminez l'intensité relative dans cette direction due à la diffraction à l'aide de l'équation 4.3.11.
Solution
D'après le chapitre sur les interférences, nous savons que les franges d'interférence brillantes se produisent à\(d \, sin \, \theta = m \lambda\), ou
\[\sin \, \theta = \dfrac{m\lambda}{d}. \nonumber \]
À partir de l'équation 4.3.11,
\[I = I_0 \left(\dfrac{\sin \, \beta}{\beta}\right)^2 \nonumber \]
où
\[\beta = \dfrac{\phi}{2} = \dfrac{\pi a \sin \, \theta}{\lambda}. \nonumber \]
En remplaçant par le haut,
\[\beta = \dfrac{\pi a \sin \, \theta}{\lambda} = \dfrac{\pi a}{\lambda} \cdot \dfrac{m\lambda}{d} = \dfrac{m\pi a}{d}. \nonumber \]
Pour\(a = 2\lambda, \, d = 6 \lambda\), et\(m = 1\),
\[\beta = \dfrac{(1)\pi (2\lambda)}{(6 \lambda)} = \dfrac{\pi}{3}. \nonumber \]
Ensuite, l'intensité est
\[I = I_0 \left(\dfrac{\sin \, \beta}{\beta}\right)^2 = I_0 \left(\dfrac{sin \, (\pi/3)}{\pi/3}\right)^2 = 0.684 I_0. \nonumber \]
L'importance
Notez que cette approche est relativement simple et donne un résultat presque identique à celui de l'analyse plus complexe utilisant des phaseurs pour déterminer les valeurs d'intensité de l'interférence à double fente (ligne fine sur la figure\(\PageIndex{1}\)). L'approche par phaseur tient compte de la pente descendante de l'intensité de diffraction (ligne bleue), de sorte que le pic près de m=1 se produit à une valeur de θ légèrement inférieure à celle que nous avons montrée ici.
Supposons que dans l'expérience de Young, les fentes d'une largeur de 0,020 mm soient séparées par 0,20 mm. Si les fentes sont éclairées par une lumière monochromatique d'une longueur d'onde de 500 nm, combien de franges lumineuses sont observées dans le pic central du diagramme de diffraction ?
Solution
D'après l'équation 4.2.1, la position angulaire du premier minimum de diffraction est\(\theta \approx sin \, \theta = \dfrac{\lambda}{a} = \dfrac{5.0 \times 10^{-7}m}{2.0 \times 10^{-5}m} = 2.5 \times 10^{-2} rad\).
En utilisant\(d \sin \, \theta = m \lambda\) pour\(\theta = 2.5 \times 10^{-2} rad\), nous trouvons
\[m = \dfrac{d \, sin \, \theta}{\lambda} = \dfrac{(0.20 \, mm)(2.5 \times 10^{-2} rad)}{(5.0 \times 10^{-7}m)} = 10, \nonumber \]
qui est l'ordre d'interférence maximal qui s'insère dans le pic central. Nous\(m=±10\) remarquons que les commandes manquantes\(θ\) correspondent exactement. En conséquence, nous observons des franges lumineuses pour
m = −9, −8, −7, −6, −5, −4, −3, −2, −1, 0, +1, +2, +3, +4, +5, +6, +7, +8 et +9
pour un total de 19 franges lumineuses.
Pour l'expérience de l'exemple\(\PageIndex{2}\), montrez que m=20 est également un ordre manquant.
Solution
À partir de\(d \, \sin \, \theta = m\lambda\), le maximum d'interférence se produit à\(2.87^o\) pour\(m = 20\). D'après l'équation 4.2.1, il s'agit également de l'angle pour le deuxième minimum de diffraction. (Remarque : Les deux équations utilisent l'indice m mais font référence à des phénomènes distincts.)
Découvrez les effets de la diffraction à double fente. Dans cette simulation écrite par Fu-Kwun Hwang, sélectionnez N=2 à l'aide du curseur et voyez ce qui se passe lorsque vous contrôlez la largeur de la fente, la séparation des fentes et la longueur d'onde. Pouvez-vous rendre une commande « manquante » ?


