Skip to main content
Global

4.3 : Intensité de la diffraction à fente unique

  1. Last updated
  2. Save as PDF
  • Page ID
    189620

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objectifs d'apprentissage

    À la fin de cette section, vous serez en mesure de :

    • Calculer l'intensité par rapport au maximum central des pics de diffraction à fente unique
    • Calculez l'intensité par rapport au maximum central d'un point arbitraire de l'écran

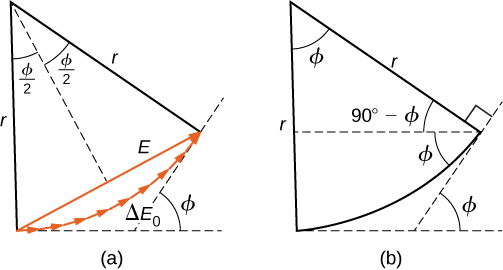
    Pour calculer l'intensité du diagramme de diffraction, nous suivons la méthode des phaseurs utilisée pour les calculs avec des circuits à courant alternatif dans des circuits à courant alternatif. Si l'on considère qu'il existe des sources de\(N\) Huygens à travers la fente illustrée précédemment, chaque source étant séparée par une distance A/n de ses voisines adjacentes, la différence de trajet entre les ondes provenant de sources adjacentes atteignant le point arbitraire\(P\) sur l'écran est de\((a/N) \, \sin \theta\). Cette distance équivaut à une différence de phase de\((2\pi a/\lambda N) \, \sin \, \theta\). Le diagramme des phaseurs des ondes arrivant au point dont la position angulaire\(\theta\) est représentée sur la figure\(\PageIndex{1}\). L'amplitude du phaseur pour chaque ondelette de Huygens est\(\Delta E_0\), l'amplitude du phaseur résultant est\(E\), et la différence de phase entre les ondelettes provenant de la première et de la dernière source est

    \[\phi = \left(\dfrac{2\pi}{\lambda}\right) \, a \, \sin \theta. \nonumber \]

    Avec\(N → ∞\), le diagramme des phaseurs se rapproche d'un arc circulaire de longueur\(N \Delta E_0\) et de rayon\(r\). Comme la longueur de l'arc est\(N \Delta E_0\) quelconque\(ϕ\), le rayon\(r\) de l'arc doit diminuer à mesure qu'il\(ϕ\) augmente (ou de manière équivalente, lorsque les phaseurs forment des spirales plus serrées).

    La figure a montre un arc avec des phaseurs étiquetés delta E indice 0. Cela sous-tend un angle au centre du cercle, à travers deux lignes étiquetées r. Cet angle est divisé en deux et chaque moitié est étiquetée phi par 2. Les extrémités de l'arc sont reliées par une flèche nommée E. La tangente à l'une des extrémités de l'arc est horizontale. La tangente à l'autre extrémité de l'arc forme un angle phi avec l'horizontale. La figure b montre l'arc et l'angle phi qu'il sous-tend. Une ligne pointillée s'étend d'une extrémité de l'arc à la ligne opposée r. Elle est perpendiculaire à r. Elle fait un angle phi avec l'arc et un angle 90 moins phi avec la droite r adjacente.
    Figure\(\PageIndex{1}\) : (a) Diagramme de phaseur correspondant à la position angulaire θθ dans le diagramme de diffraction à fente unique. La différence de phase entre les ondelettes provenant de la première et de la dernière source est de\(\phi = (2\pi /\lambda)a \, sin \, \theta\). (b) La géométrie du diagramme des phaseurs.

    Le diagramme de phaseur pour φ = 0 (le centre du diagramme de diffraction) est illustré sur la figure en\(\PageIndex{1a}\) utilisant N = 30. Dans ce cas, les phaseurs sont placés bout à bout sur une ligne droite de longueur\(N \Delta E_0\), le rayon r passe à l'infini et la résultante a sa valeur maximale\(E = N\Delta E_0\). L'intensité de la lumière peut être obtenue en utilisant la relation\(I = \dfrac{1}{2} c \epsilon_0 E^2\) des ondes électromagnétiques. L'intensité du maximum est alors

    \[I_0 = \dfrac{1}{2} c\epsilon_0 (N \Delta E_0)^2 = \dfrac{1}{2\mu_0 c}(N\Delta E_0)^2, \nonumber \]

    où\(\epsilon_0 = 1/\mu_0 c^2\). Les diagrammes des phaseurs pour les deux premiers zéros du diagramme de diffraction sont présentés sur la figure\(\PageIndex{1b}\) et la figure\(\PageIndex{1d}\). Dans les deux cas, les phaseurs s'additionnent à zéro, après avoir fait tourner\(\phi = 2\pi\) rad pour m = 1 et\(4 \pi\) rad pour m = 2.

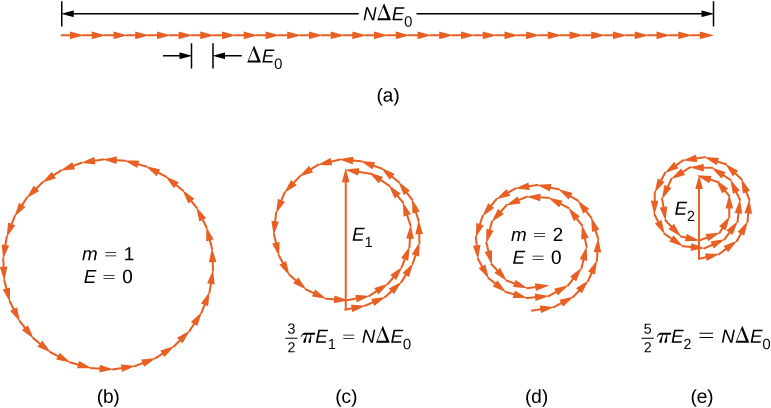
    La figure a montre 30 phaseurs sur une ligne de longueur N delta E indice 0. La longueur d'un phaseur est le delta E, indice 0. La figure b montre un cercle avec des phaseurs pointant dans le sens inverse des aiguilles d'une montre. Ceci est noté m égal à 1, E égal à 0. La figure c montre les phaseurs le long d'un cercle. Ils partent du bas et font le tour du cercle une fois et demie dans le sens inverse des aiguilles d'une montre. Une flèche allant du point de départ au point d'arrivée est étiquetée E1. Elle forme le diamètre du cercle. La figure c est étiquetée 3 par 2 pi E1 égal à N delta E0. La figure d montre les phaseurs le long d'un cercle. Ils partent du bas et font deux fois le tour du cercle dans le sens inverse des aiguilles d'une montre. Le chiffre est noté m égal à 2, E égal à 0. La figure e montre les phaseurs le long d'un cercle. Ils partent du bas et font deux fois et demie le tour du cercle dans le sens inverse des aiguilles d'une montre. Une flèche allant du point de départ au point d'arrivée est étiquetée E2. Elle forme le diamètre du cercle. La figure c est étiquetée 5 par 2 pi E2 égal à N delta E0.
    Figure\(\PageIndex{2}\) : Diagrammes de phaseurs (avec 30 phaseurs) pour différents points du diagramme de diffraction à fente unique. Les rotations multiples autour d'un cercle donné ont été légèrement séparées afin que les phaseurs soient visibles. (a) Maximum central, (b) premier minimum, (c) premier maximum au-delà du maximum central, (d) deuxième minimum et (e) deuxième maximum au-delà du maximum central.

    Les deux maxima suivants au-delà des maxima centraux sont représentés par les diagrammes des phases des parties (c) et (e). Dans la partie (c), les phaseurs ont pivoté à travers\(\phi = 3\pi\) rad et ont formé un phaseur résultant de magnitude\(E_1\). La longueur de l'arc formé par les phaseurs est de\(N\Delta E_0\). Comme cela correspond à 1,5 rotation autour d'un cercle de diamètre\(E_1\), nous avons

    \[\dfrac{3}{2} \pi E_1 = N \Delta E_0, \nonumber \]

    donc

    \[E_1 = \dfrac{2N\Delta E_0}{3\pi} \nonumber \]

    et

    \[I_1 = \dfrac{1}{2\mu_0 c}E_1^2 = \dfrac{4(N\Delta E_0)^2}{(9\pi^2)(2\mu_0c)} = 0.045 I_0, \nonumber \]

    où

    \[I_0 = \dfrac{(N\Delta E_0)^2}{2\mu_0 c}. \nonumber \]

    Dans la partie (e), les phaseurs ont pivoté selon\(\phi = 5\pi\) rad, ce qui correspond à 2,5 rotations autour d'un cercle de diamètre\(E_2\) et de longueur d'arc\(N\Delta E_0\). Cela se traduit par\(I_2 = 0.016 I_0\). La preuve est laissée à l'étudiant sous forme d'exercice (Exercice 4.119).

    Ces deux maxima correspondent en fait à des valeurs de φ légèrement inférieures à\(3\pi\) rad et\(5\pi\) rad. Comme la longueur totale de l'arc du diagramme de phaseur est toujours\(N \Delta E_0\), le rayon de l'arc diminue à mesure qu'il\(ϕ\) augmente. Par conséquent,\(E_1\) et s'\(E_2\)avèrent légèrement plus grands pour les arcs qui ne se sont pas tout à fait incurvés à travers\(3\pi\) rad et\(5\pi\) rad, respectivement. Les valeurs exactes de\(ϕ\) pour les maxima sont étudiées dans l'exercice 4.120. En résolvant ce problème, vous constaterez qu'ils sont inférieurs à, mais très proches de,\(\phi = 3\pi, \, 5\pi, \, 7\pi,\)... rad.

    Pour calculer l'intensité à un point arbitraire de\(P\) l'écran, nous revenons au diagramme des phaseurs de la Figure\(\PageIndex{1}\). Puisque l'arc sous-tend un angle φ au centre du cercle,

    \[N\Delta E_0 = r\phi \label{eq10} \]

    et

    \[\sin \left(\dfrac{\phi}{2}\right) = \dfrac{E}{2r}. \label{eq11} \]

    où\(E\) est l'amplitude du champ résultant. En résolvant l'équation \ ref {eq11}\(E\) puis en la remplaçant\(r\) par l'équation \ ref {eq10}, nous trouvons

    \[\begin{align*} E &= 2r \, \sin \, \dfrac{\phi}{2} \\[5pt] &= 2\dfrac{N\Delta E_0}{\phi} \sin \, \dfrac{\phi}{2}. \end{align*} \nonumber \]

    En train de définir

    \[\beta = \dfrac{\phi}{2} = \dfrac{\pi a \, \sin \, \theta}{\lambda} \label{4.2} \]

    nous obtenons

    \[E = N\Delta E_0 \dfrac{\sin \, \beta}{\beta} \label{eq15} \]

    L'équation \ ref {eq15} met en relation l'amplitude du champ résultant en tout point du diagramme de diffraction à l'amplitude\(N \Delta E_0\) au maximum central. L'intensité est proportionnelle au carré de l'amplitude, donc

    \[I = I_0 \left(\dfrac{\sin \, \beta}{\beta}\right)^2 \label{eq20} \]

    où\(I_0 = (N\delta E_0)^2/2\mu_0 c\) est l'intensité au centre du motif.

    Pour le maximum central, φ = 0, β est également nul et nous voyons dans la règle de l'Hôpital que\(\lim_{\beta \rightarrow 0}(sin \, \beta/\beta) = 1\), donc\(lim_{\phi \rightarrow 0}I = I_0\). Pour le maximum suivant,\(\phi = 3\pi\) rad, nous avons\(\beta = 3\pi/2\) rad et lorsqu'il est remplacé par l'équation \ ref {eq20}, il donne

    \[I_1 = I_0 \left(\dfrac{\sin \, 3\pi/2}{3\pi/2}\right)^2 = 0.045 I_0, \nonumber \]

    en accord avec ce que nous avons découvert plus tôt dans cette section en utilisant les diamètres et les circonférences des diagrammes de phaseurs. La substitution de\(\phi = 5\pi\) rad dans l'équation \ ref {eq20} donne un résultat similaire pour\(I_2\).

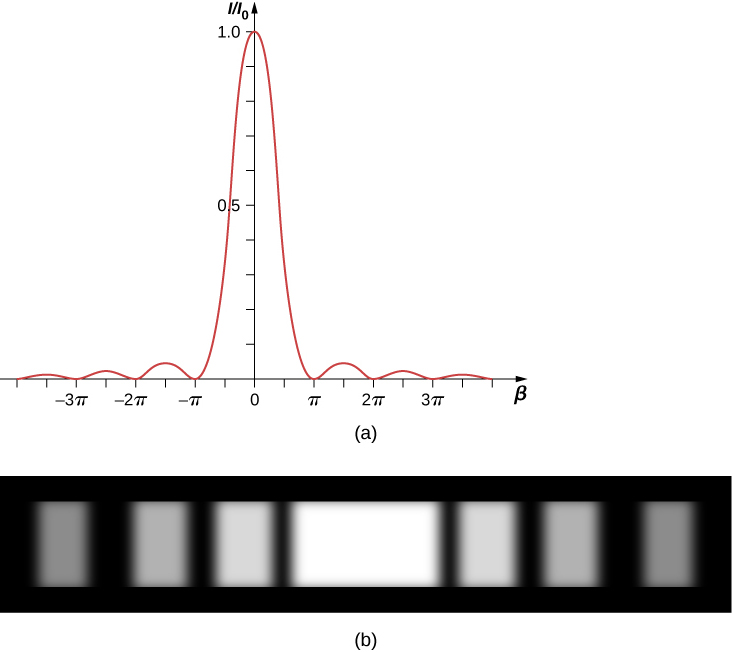
    Un diagramme de l'équation \ ref {eq20} est illustré sur la figure\(\PageIndex{3}\) et, juste en dessous, se trouve une photographie d'un diagramme de diffraction réel. Notez que le pic central est beaucoup plus lumineux que les autres et que les zéros du motif sont situés aux points où\(sin \, \beta = 0\), ce qui se produit lorsque\(\beta = m\pi\) rad. Cela correspond à

    \[\dfrac{\pi a \, \sin \theta}{\lambda} = m\pi, \nonumber \]

    ou

    \[a \, \sin \, \theta = m \lambda, \nonumber \]

    que nous avons dérivée pour l'interférence destructrice d'une seule fente précédemment.

    La figure a montre un graphique de I par I0 par rapport à bêta. Il y a une crête au centre du graphique en bêta égale à 0. La valeur y de ce paramètre est 1. Le graphique présente des ondulations des deux côtés qui diminuent au fur et à mesure que vous vous dirigez vers l'extérieur. Le graphique comporte des zéros à moins 3 pi, moins 2 pi, moins pi, pi, 2 pi, 3 pi. La figure b montre une bande présentant une alternance de zones claires et sombres. La partie centrale est la plus lumineuse.
    Figure\(\PageIndex{3}\) : (a) La distribution d'intensité calculée d'un diagramme de diffraction à fente unique. (b) Le diagramme de diffraction réel.
    Exemple\(\PageIndex{1}\): Intensity in Single-Slit Diffraction

    La lumière d'une longueur d'onde de 550 nm traverse une fente d'une largeur de 2,00 µm et produit un diagramme de diffraction similaire à celui illustré à la figure\(\PageIndex{3a}\).

    1. Déterminez les emplacements des deux premiers minima en termes d'angle par rapport au maximum central.
    2. Déterminez l'intensité par rapport au maximum central à mi-chemin entre ces deux minima.

    Stratégie

    Les minima sont donnés par l'équation 4.2.1,\(a \, sin \, \theta = m\lambda\). Les deux premiers minima sont pour m = 1 et m = 2. L'équation \ ref {eq20} et l'équation \ ref {4.2} peuvent être utilisées pour déterminer l'intensité une fois que l'angle a été déterminé.

    Solution
    1. La résolution de l'équation 4.2.1 pour θ nous donne\(\theta_m = \sin^{-1}(m\lambda/a)\), de sorte que

      \[\theta_1 = \sin^{-1} \left(\dfrac{(+1)(550 \times 10^{-9} m)}{2.00 \times 10^{-6}m}\right) = +16.0° \nonumber \]

      et

      \[\theta_2 = \sin^{-1} \left(\dfrac{(+2)(550 \times 10^{-9}m)}{2.00 \times 10^{-6}m}\right) = +33.4°. \nonumber \]

    2. Le point à mi-chemin entre\(\theta_1\) et\(\theta_2\) est

      \[\theta = (\theta_1 + \theta_2) /2 = (16.0° + 33.4°)/2 = 24.7°. \nonumber \]

    L'équation \ ref {4.2} donne

    \[\beta = \dfrac{\pi a \, sin \, \theta}{\lambda} = \dfrac{\pi (2.00 \times 10^{-6}m) \, \sin \, (24.7°)}{(550 \times 10^{-9}m)} = 1.52\pi \, or \, 4.77 \, rad. \nonumber \]

    À partir de l'équation \ ref {eq20}, nous pouvons calculer

    \[\dfrac{I}{I_0} = \left(\dfrac{\sin \, \beta}{\beta}\right)^2 = \left(\dfrac{\sin \, (4.77)}{4.77}\right)^2 = \left(\dfrac{-0.9985}{4.77}\right)^2 = 0.044. \nonumber \]

    L'importance

    Cette position, à mi-chemin entre deux minima, est très proche de l'emplacement du maximum, attendu à proximité de\(\beta = 3\pi/2\), ou\(1.5\pi\).

    Exercice\(\PageIndex{1}\)

    Pour l'expérience présentée dans Example\(\PageIndex{1}\), à quel angle par rapport au centre se trouve le troisième maximum et quelle est son intensité par rapport au maximum central ?

    Réponse

    \(74.3^o\),\(0.0083 I_0\)

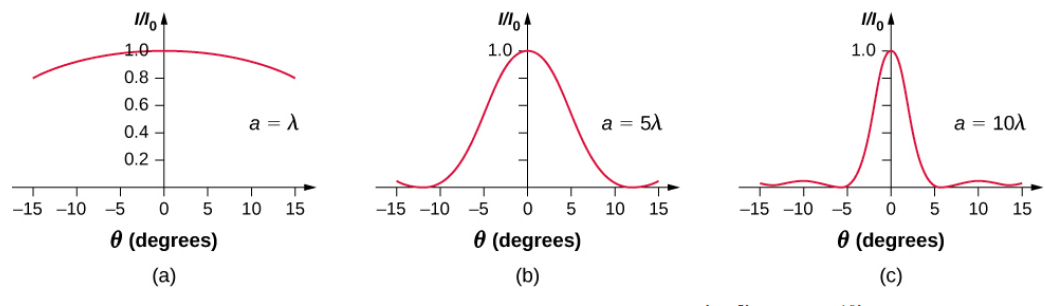
    Si la largeur de la fente\(a\) est modifiée, la distribution de l'intensité change, comme illustré sur la figure\(\PageIndex{4}\). Le pic central est réparti sur la région de\(sin \, \theta = -\lambda/a\) à\(sin \, \theta = +\lambda/a\). Pour un petit θ, cela correspond à une largeur angulaire\(\Delta \theta \approx 2\lambda /a\). Ainsi, une augmentation de la largeur de la fente entraîne une diminution de la largeur du pic central. Pour une fente de ≫ λ, le pic central est très net, alors que si a ≈ λ, il devient assez large.

    Les figures a à c montrent des graphiques de I par I0 par rapport à thêta en degrés. Chacune possède une crête d'onde dont la valeur y est 1 à x=0. La figure a, étiquetée égale à lambda, a un grand arc. La figure b, étiquetée a égale à 5 lambda, a une crête plus étroite. Il a des zéros entre 10 et 15 environ et entre moins 10 et moins 15. La figure c, étiquetée égale à 10 lambda, possède une crête étroite. Il a des zéros à plus et moins 5, approximativement entre 10 et 15 et entre moins 10 et moins 15.
    Figure\(\PageIndex{4}\) : Motifs de diffraction à fente unique pour différentes largeurs de fente. Lorsque la largeur de la fente a augmente de a =λ à 5λ puis à 10λ, la largeur du pic central diminue à mesure que les angles des premiers minima diminuent, comme le prédit l'équation 4.2.1.
    Simulation de diffraction

    Une expérience de diffraction en optique peut demander beaucoup de préparation, mais cette simulation d'Andrew Duffy offre non seulement une mise en place rapide, mais également la possibilité de modifier instantanément la largeur de la fente. Lancez la simulation et sélectionnez « Fente unique ». Vous pouvez régler la largeur de la fente et voir l'effet sur le diagramme de diffraction sur un écran et sous forme de graphique.