4.2 : Diffraction à fente unique

Last updated
Save as PDF

Page ID: 189610

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objectifs d'apprentissage

À la fin de cette section, vous serez en mesure de :

Expliquer le phénomène de diffraction et les conditions dans lesquelles il est observé
Décrire la diffraction à travers une seule fente

Après avoir traversé une ouverture étroite (ouverture), une onde se propageant dans une direction spécifique a tendance à se propager. Par exemple, les ondes sonores qui pénètrent dans une pièce par une porte ouverte peuvent être entendues même si l'auditeur se trouve dans une partie de la pièce où la géométrie de la propagation des rayons impose qu'il ne doit y avoir que du silence. De même, les vagues océaniques passant par une ouverture d'un brise-lames peuvent se propager dans toute la baie intérieure. (Figurine\(\PageIndex{1}\)). La propagation et la flexion du son et des vagues de l'océan sont deux exemples de diffraction, c'est-à-dire la flexion d'une onde autour des bords d'une ouverture ou d'un obstacle, phénomène qui se manifeste par tous les types d'ondes.

Photographie montrant la vue de dessus d'un brise-lames près d'une plage. Il y a une ouverture dans le brise-lames qui permet aux vagues d'entrer. — Figure\(\PageIndex{1}\) : En raison de la diffraction des vagues, les vagues océaniques qui pénètrent par une ouverture dans un brise-lames peuvent se propager dans toute la baie. (crédit : modification des données cartographiques de Google Earth)

La diffraction des ondes sonores est évidente pour nous parce que les longueurs d'onde dans la région audible sont approximativement de la même taille que les objets qu'elles rencontrent, une condition qui doit être remplie pour pouvoir observer facilement les effets de diffraction. Comme les longueurs d'onde de la lumière visible varient d'environ 390 à 770 nm, la plupart des objets ne diffractent pas la lumière de manière significative. Cependant, il arrive que les ouvertures soient suffisamment petites pour que la diffraction de la lumière soit observable. Par exemple, si vous placez votre majeur et votre index près l'un de l'autre et que vous regardez une ampoule par l'ouverture, vous pouvez voir un motif de diffraction assez clair, composé de lignes claires et foncées parallèles à vos doigts.

Diffraction à travers une seule fente

La lumière traversant une seule fente forme un diagramme de diffraction quelque peu différent de ceux formés par des fentes doubles ou des réseaux de diffraction, dont nous avons parlé dans le chapitre sur les interférences. La figure\(\PageIndex{2}\) montre un diagramme de diffraction à fente unique. Notez que le maximum central est supérieur aux maxima de chaque côté et que l'intensité diminue rapidement de chaque côté. En revanche, un réseau de diffraction produit des lignes régulièrement espacées qui s'atténuent lentement de chaque côté du centre.

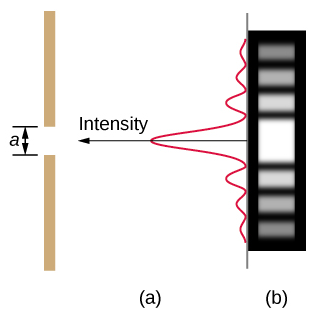
La figure a montre une ligne verticale sur le côté gauche. Il y a un écart de longueur a. Une onde verticale est représentée sur la droite. La vague a une haute crête au centre, correspondant à la fente. La vague s'atténue à la fois en haut et en bas. Une flèche le long de la crête centrale de la vague, pointant vers la fente, est étiquetée intensité. La figure b montre une bande avec des lignes claires et foncées marquées horizontalement. La ligne centrale, correspondant à la fente, est la plus brillante. — Figure\(\PageIndex{2}\) : Diagramme de diffraction à fente unique. a) La lumière monochromatique traversant une seule fente possède un maximum central et de nombreux maxima plus petits et plus faibles de chaque côté. Le maximum central est six fois plus élevé que celui indiqué. (b) Le diagramme montre le maximum central brillant et les maxima les plus faibles et les plus faibles de chaque côté.

L'analyse de la diffraction à fente unique est illustrée sur la figure\(\PageIndex{2}\). Ici, la lumière arrive à la fente, l'éclaire de manière uniforme et est en phase sur toute sa largeur. Nous considérons ensuite la lumière se propageant vers l'avant à partir de différentes parties de la même fente. Selon le principe de Huygens, chaque partie du front d'onde dans la fente émet des ondelettes, comme nous l'avons vu dans La nature de la lumière. Ce sont comme des rayons qui commencent par phase et se dirigent dans toutes les directions. (Chaque rayon est perpendiculaire au front d'onde d'une ondelette.) En supposant que l'écran soit très éloigné par rapport à la taille de la fente, les rayons se dirigeant vers une destination commune sont presque parallèles. Lorsqu'ils se déplacent en ligne droite, comme dans la partie (a) de la figure, ils restent en phase, et nous observons un maximum central. Cependant, lorsque les rayons se déplacent selon un angle θ par rapport à la direction d'origine du faisceau, chaque rayon parcourt une distance différente jusqu'à un emplacement commun, et ils peuvent arriver en phase ou hors phase. Dans la partie (b), le rayon partant du bas parcourt une distance d'une longueur d'onde λ plus loin que le rayon partant du haut. Ainsi, un rayon provenant du centre parcourt une distance λ/2 inférieure à celle du bord inférieur de la fente, arrive hors phase et interfère de manière destructive. Un rayon légèrement au-dessus du centre et un rayon légèrement au-dessus du bas s'annulent également mutuellement. En fait, chaque rayon de la fente interfère de manière destructrice avec un autre rayon. En d'autres termes, une annulation par paire de tous les rayons se traduit par un minimum d'intensité sombre à cet angle. Par symétrie, un autre minimum se produit sous le même angle à droite de la direction incidente (vers le bas de la figure) de la lumière.

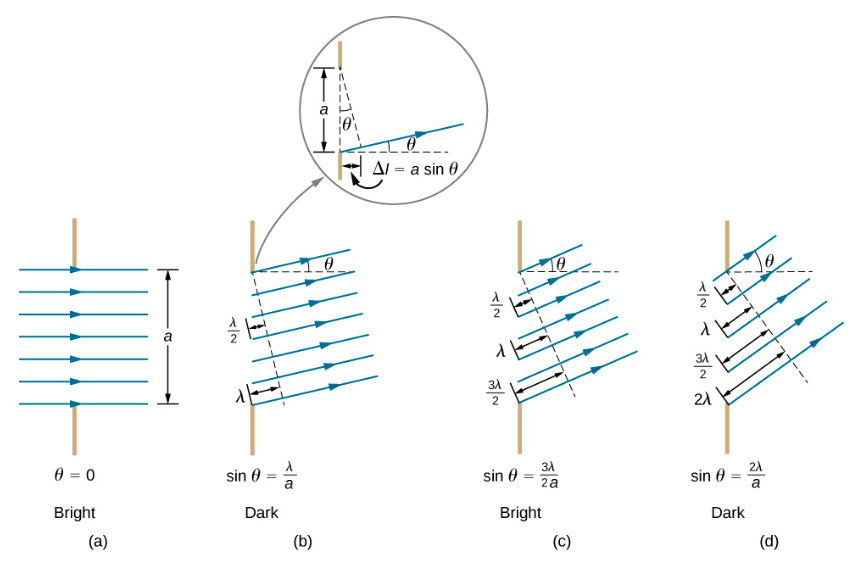
La figure a montre des rayons horizontaux passant de gauche à droite à travers une fente verticale de longueur a. Ceci est étiqueté thêta égal à zéro, brillant. La figure b montre les rayons traversant la fente selon un angle thêta par rapport à l'horizontale. Il est étiqueté sinus thêta égal à lambda par a, foncé. Une ligne pointillée perpendiculaire aux rayons touche le haut de la fente. Sa distance perpendiculaire depuis le bas de la fente est lambda et celle depuis le centre de la fente est lambda de 2. Une vue séparée montre que la ligne pointillée forme un angle thêta par rapport à la verticale. Il coupe le rayon en partant du bas de la fente en un point particulier. La distance horizontale entre ce point et la fente est un delta l égal à un sinus thêta. La figure c montre les rayons traversant la fente selon un angle thêta par rapport à l'horizontale. Il est étiqueté sinus thêta égal à 3 lambda par 2 a, brillant. Une ligne pointillée perpendiculaire aux rayons touche le haut de la fente. Sa distance perpendiculaire par rapport au bas de la fente est de 3 lambda par 2. La figure d montre les rayons traversant la fente selon un angle thêta par rapport à l'horizontale. Il est étiqueté sinus thêta égal à 2 lambda par a, foncé. Une ligne pointillée perpendiculaire aux rayons touche le haut de la fente. Sa distance perpendiculaire par rapport au bas de la fente est de 2 lambda. — Figure\(\PageIndex{3}\) : La lumière traversant une seule fente est diffractée dans toutes les directions et peut interférer de manière constructive ou destructive, selon l'angle. La différence de longueur de trajet pour les rayons provenant de chaque côté de la fente est considérée comme étant\(\sin θ\) a.

À l'angle le plus grand indiqué dans la partie (c), les longueurs de trajet diffèrent\(3λ/2\) pour les rayons provenant du haut et du bas de la fente. Un rayon parcourt une distance\(λ\) différente de celle du rayon depuis le bas et arrive en phase, interférant de manière constructive. Deux rayons, venant chacun légèrement au-dessus de ces deux rayons, s'additionnent également de manière constructive. La plupart des rayons provenant de la fente ont un autre rayon avec lequel ils peuvent interférer de manière constructive, et un maximum d'intensité se produit à cet angle. Cependant, tous les rayons n'interfèrent pas de manière constructive dans cette situation, de sorte que le maximum n'est pas aussi intense que le maximum central. Enfin, dans la partie (d), l'angle indiqué est suffisamment grand pour produire un second minimum. Comme le montre la figure, la différence de longueur de trajet pour les rayons provenant de chaque côté de la fente est de\(a \sin \theta\), et nous voyons qu'un minimum destructif est obtenu lorsque cette distance est un multiple entier de la longueur d'onde.

Ainsi, pour obtenir une interférence destructrice pour une seule fente,

\[\underbrace{a \sin θ = mλ}_{\text{destructive interference}} \nonumber \]

où

\(m = ±1, ±2, ±3,...\),
\(a\)est la largeur de la fente,
\(λ\)est la longueur d'onde de la lumière,
\(θ\)est l'angle par rapport à la direction initiale de la lumière, et
\(m\)est l'ordre du minimum.

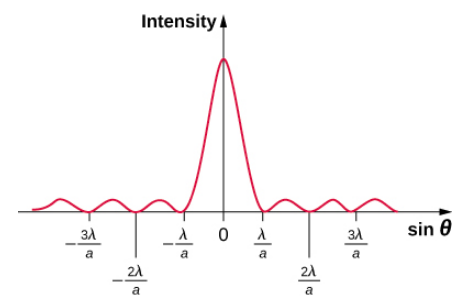
La figure\(\PageIndex{3}\) montre un graphique de l'intensité des interférences à fente unique, et il est évident que les maxima de chaque côté du maximum central sont beaucoup moins intenses et moins larges. Cet effet est exploré dans Diffraction à double fente.

La figure montre un graphique de l'intensité par rapport au sinus thêta. L'intensité est maximale à un sinus thêta égal à 0. Il y a des crêtes de vagues plus petites de chaque côté, à un sinus thêta égal à moins 2 lambda a, moins lambda a, lambda a, 2 lambda a, etc. — Figure\(\PageIndex{3}\) : Un graphique de l'intensité de diffraction à fente unique montrant que le maximum central est plus large et beaucoup plus intense que ceux situés sur les côtés. En fait, le maximum central est six fois plus élevé que celui indiqué ici.

Exemple\(\PageIndex{1}\): Calculating Single-Slit Diffraction

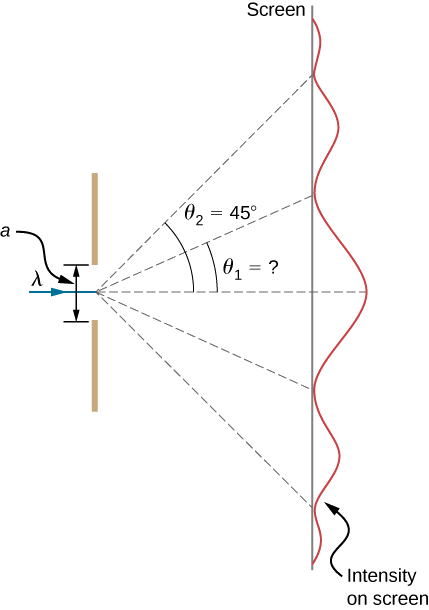
La lumière visible d'une longueur d'onde de 550 nm tombe sur une seule fente et produit son deuxième minimum de diffraction à un angle de 45,0° par rapport à la direction incidente de la lumière, comme sur la figure\(\PageIndex{5}\).

Quelle est la largeur de la fente ?
Sous quel angle est produit le premier minimum ?

La figure montre une ligne verticale sur la gauche. Elle comporte une fente au milieu, de longueur a. Un rayon marqué lambda passe horizontalement à travers la fente. Cela se divise en 5 lignes pointillées qui tombent sur un écran. L'écran s'affiche sous la forme d'une ligne verticale. Sur les cinq lignes pointillées, deux forment les angles thêta 1 et thêta 2 avec l'horizontale. Theta 2 fait 45 degrés. Le Thêta 1 est plus petit que le thêta 2 et est inconnu. L'intensité affichée à l'écran est représentée par une onde verticale. La crête au centre, où une ligne pointillée horizontale partant du centre de la fente tombe sur l'écran, est la plus grande. La vague s'atténue en haut et en bas. Les quatre lignes pointillées restantes correspondent aux creux de la vague. — Figure\(\PageIndex{5}\) : Dans cet exemple, nous analysons un graphique du diagramme de diffraction à fente unique.

Stratégie

À partir des informations fournies, et en supposant que l'écran est éloigné de la fente, nous pouvons utiliser l'équation d'\(a \sin θ = mλ\)abord pour trouver\(a\), puis de nouveau pour trouver l'angle du premier minimum\(\theta_1\).

Solution

On nous donne cela\(λ=550\,nm\)\(m=2\), et\(\theta_2 = 45.0°\). La résolution de\(a \, \sin \, \theta = m\lambda\) l'équation\(a\) et la substitution de valeurs connues donnent
\[a = \frac{m\lambda}{\sin \, \theta_2} = \frac{2(550 \, nm)}{\sin \, 45.0°} = \frac{1100 \times 10^{-9} m}{0.707} = 1.56 \times 10^{-6} m. \nonumber \]
La résolution de\(a \, \sin \, \theta = m\lambda\) l'équation\(\sin \, \theta_1\) et la substitution des valeurs connues donnent
\[\sin \, \theta_1 = \frac{m\lambda}{a} = \frac{1(550 \times 10^{-9}m)}{1.56 \times 10^{-6}m}. \nonumber \]
Ainsi, l'angle\(\theta_1\) est
\[\theta_1 = \sin^{-1}0.354 = 20.7°. \nonumber \]

L'importance

On voit que la fente est étroite (elle n'est que quelques fois supérieure à la longueur d'onde de la lumière). Cela est cohérent avec le fait que la lumière doit interagir avec un objet de taille comparable à sa longueur d'onde afin de présenter des effets d'onde significatifs tels que ce diagramme de diffraction à fente unique. Nous voyons également que le maximum central s'étend de 20,7° de part et d'autre du faisceau d'origine, pour une largeur d'environ 41°. L'angle entre le premier et le second minima n'est que d'environ 24° (45,0°−20,7°). Ainsi, le second maximum n'est que deux fois moins large que le maximum central.

Exercice\(\PageIndex{1}\)

Supposons que la largeur de la fente dans l'exemple\(\PageIndex{1}\) soit augmentée à\(1.8 \times 10^{-6} m\). Quelles sont les nouvelles positions angulaires pour les premier, deuxième et troisième minima ? Y aurait-il un quatrième minimum ?

Réponse: \(17.8^o\),\(37.7^o\),\(66.4^o\) ; non