13.4 : Mouvement dans l'espace
- Page ID
- 197193
- Décrivez les vecteurs de vitesse et d'accélération d'une particule se déplaçant dans l'espace.
- Expliquer les composantes tangentielles et normales de l'accélération.
- Expliquez les lois de Kepler sur le mouvement planétaire.
Nous avons maintenant vu comment décrire des courbes dans le plan et dans l'espace, et comment déterminer leurs propriétés, telles que la longueur et la courbure de l'arc. Tout cela nous amène à l'objectif principal de ce chapitre, qui est de décrire le mouvement le long de courbes planes et de courbes spatiales. Nous disposons désormais de tous les outils dont nous avons besoin ; dans cette section, nous rassemblons ces idées et examinons comment les utiliser.
Vecteurs de mouvement dans le plan et dans l'espace
Notre point de départ est d'utiliser des fonctions à valeurs vectorielles pour représenter la position d'un objet en fonction du temps. Tous les matériaux suivants peuvent être appliqués à des courbes dans le plan ou à des courbes spatiales. Par exemple, lorsque nous examinons l'orbite des planètes, les courbes qui définissent ces orbites se situent toutes dans un plan car elles sont elliptiques. Cependant, une particule se déplaçant le long d'une hélice se déplace sur une courbe en trois dimensions.
\(\vecs r(t)\)Soit une fonction à valeur vectorielle différenciable deux fois du paramètre\(t\) qui représente la position d'un objet en fonction du temps.
Le vecteur\(\vecs v(t)\) de vitesse de l'objet est donné par
\[\text{Velocity}\,=\vecs v(t)=\vecs r′(t). \label{Eq1} \]
Le vecteur d'accélération\(\vecs a(t)\) est défini comme étant
\[\text{Acceleration}\,=\vecs a(t)=\vecs v′(t)=\vecs r″(t). \label{Eq2} \]
La vitesse est définie comme étant
\[\mathrm{Speed}\,=v(t)=‖\vecs v(t)‖=‖\vecs r′(t)‖=\dfrac{ds}{dt}. \label{Eq3} \]
Comme elles\(\vecs{r}(t)\) peuvent être en deux ou trois dimensions, ces fonctions à valeur vectorielle peuvent comporter deux ou trois composants. En deux dimensions, nous définissons\(\vecs{r}(t)=x(t) \hat{\mathbf i}+y(t) \hat{\mathbf j}\) et en trois dimensions\(\vecs r(t)=x(t) \hat{\mathbf i}+y(t) \hat{\mathbf j}+z(t) \hat{\mathbf k}\). Ensuite, la vitesse, l'accélération et la vitesse peuvent être écrites comme indiqué dans le tableau suivant.
| Quantité | Deux dimensions | Trois dimensions |
|---|---|---|
| Poste | \(\vecs{r}(t)=x(t) \hat{\mathbf i}+y(t) \hat{\mathbf j}\) | \(\vecs{r}(t)=x(t) \hat{\mathbf i}+y(t) \hat{\mathbf j}+z(t) \hat{\mathbf k}\) |
| Vitesse | \(\vecs{v}(t)=x′(t) \hat{\mathbf i}+y′(t) \hat{\mathbf j}\) | \(\vecs{v}(t)=x′(t) \hat{\mathbf i}+y′(t) \hat{\mathbf j}+z′(t) \hat{\mathbf k}\) |
| accélération | \(\vecs{a}(t)=x″(t) \hat{\mathbf i}+y″(t) \hat{\mathbf j}\) | \(\vecs{a}(t)=x″(t) \hat{\mathbf i}+y″(t) \hat{\mathbf j}+z″(t) \hat{\mathbf k}\) |
| Vitesse | \(\|\vecs{v}(t)\|= \sqrt{(x′(t))^2+(y′(t))^2}\) | \(\|\vecs{v}(t)\|=\sqrt{(x′(t))^2+(y′(t))^2+(z′(t))^2}\) |
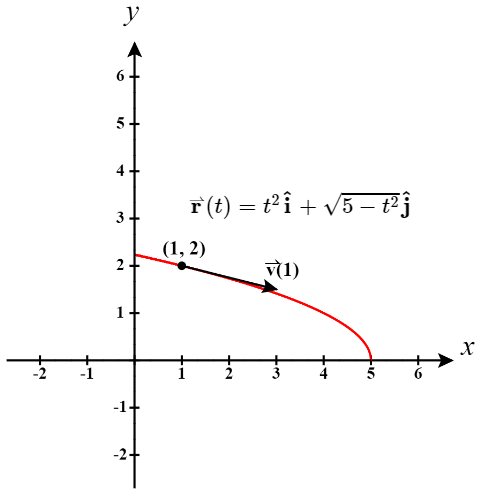
Une particule se déplace sur une trajectoire parabolique définie par la fonction à valeur vectorielle\(\vecs{r}(t)=t^2 \hat{\mathbf i}+ \sqrt{5−t^2} \hat{\mathbf j}\), qui\(t\) mesure le temps en secondes.
- Déterminez la vitesse, l'accélération et la vitesse en fonction du temps.
- Esquissez la courbe avec le vecteur de vitesse à la fois\(t=1\).
Solution
- Nous utilisons les équations \ ref {Eq1}, \ ref {Eq2} et \ ref {Eq3} :
\[ \begin{align*} \vecs{v}(t) &= \vecs{r}′(t)=2t\hat{\mathbf i}−\dfrac{t}{\sqrt{5-t^2}}\hat{\mathbf j} \\[4pt] \vecs{a}(t) &=\vecs{v}′(t)=2\hat{\mathbf i}−5(5−t^2)^{-\frac{3}{2}}\hat{\mathbf j} \\[4pt] ||\vecs{v}(t)|| &=||\vecs{r}′(t)|| \\[4pt] &=\sqrt{(2t)^2+\left(-\dfrac{t}{\sqrt{5-t^2}}\right)^2} \\[4pt] &=\sqrt{4t^2+\dfrac{t^2}{5-t^2}} \\[4pt] &=\sqrt{\dfrac{21t^2-4t^4}{5-t^2}}. \end{align*}\]
- Le graphique de\(\vecs{r}(t)=t^2 \hat{\mathbf i}+ \sqrt{5−t^2} \hat{\mathbf j}\) est une partie d'une parabole (Figure\(\PageIndex{1}\)).
Quand\(t=1\),\(\vecs r(1) = (1)^2 \mathbf{\hat i} + \sqrt{5-(1)^2} \mathbf{\hat j} \quad = \quad \mathbf{\hat i} + \sqrt{4} \mathbf{\hat j} \quad = \quad \mathbf{\hat i} + 2 \mathbf{\hat j}\).
Ainsi, la particule serait localisée au point\((1, 2)\) où\(t =1\).
Le vecteur de vitesse à\(t=1\) est\[ \begin{align*} \vecs{v}(1) &=\vecs{r}′(1)=2(1)\hat{\mathbf i}−\frac{1}{\sqrt{5-1^2}} \hat{\mathbf j}\quad \\[4pt] &= \quad 2\hat{\mathbf i}−\frac{1}{2}\hat{\mathbf j} \end{align*}\]
et le vecteur d'accélération at\(t=1\) est\[\vecs{a}(1)=\vecs{v}′(1)=2\hat{\mathbf i}−5(5 - 1^2)^{-3/2}\hat{\mathbf j}\quad = \quad 2\hat{\mathbf i}−\frac{5}{8}\hat{\mathbf j}. \nonumber \]
Notez que le vecteur de vitesse est tangent à la trajectoire, comme c'est toujours le cas.
Une particule se déplace sur une trajectoire définie par la fonction à valeur vectorielle\(\vecs r(t)=(t^2−3t)\,\hat{\mathbf i}+(2t−4)\,\hat{\mathbf j}+(t+2)\,\hat{\mathbf k}\), qui\(t\) mesure le temps en secondes et la distance en pieds. Déterminez la vitesse, l'accélération et la vitesse en fonction du temps.
- Allusion
-
Utilisez les équations \ ref {Eq1}, \ ref {Eq2} et \ ref {Eq3}.
- Réponse
-
\[\begin{align*}\vecs v(t) &=\vecs{r}'(t) =(2t-3)\,\hat{\mathbf i}+2\,\hat{\mathbf j}+\,\hat{\mathbf k}\\[4pt] \vecs a(t) &=\vecs v′(t) =2\,\hat{\mathbf i} \end{align*}\]
\[ ||\vecs{r}′(t)||=\sqrt{(2t-3)^2+2^2+1^2} =\sqrt{4t^2-12t+14} \nonumber \]
Les unités de vitesse et de vitesse sont les pieds par seconde, et les unités d'accélération sont les pieds par seconde au carré.
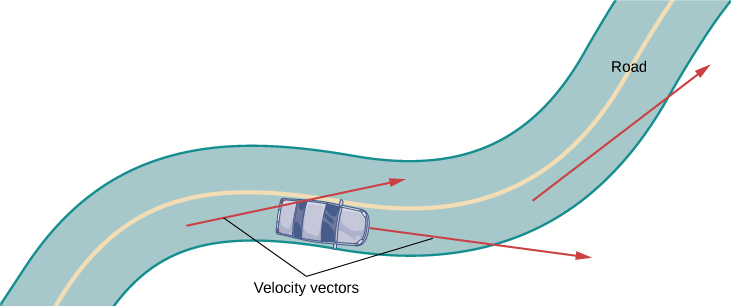
Pour mieux comprendre les vecteurs de vitesse et d'accélération, imaginez que vous conduisez sur une route sinueuse. Si vous ne tournez pas le volant, vous continuerez en ligne droite et quitterez la route. La vitesse à laquelle vous vous déplacez lorsque vous quittez la route, associée à la direction, donne un vecteur représentant votre vitesse, comme illustré sur la figure\(\PageIndex{2}\).
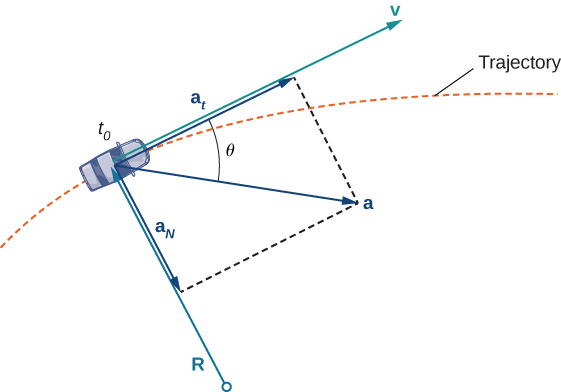
Cependant, le fait que vous deviez tourner le volant pour rester sur la route indique que votre vitesse change constamment (même si votre vitesse ne l'est pas) car votre direction change constamment pour vous permettre de rester sur la route. Lorsque vous tournez vers la droite, votre vecteur d'accélération pointe également vers la droite. Lorsque vous tournez vers la gauche, votre vecteur d'accélération pointe vers la gauche. Cela indique que vos vecteurs de vitesse et d'accélération changent constamment, que votre vitesse réelle varie ou non (Figure\(\PageIndex{3}\)).
Composantes du vecteur d'accélération
Nous pouvons combiner certains des concepts abordés dans Longueur et courbure de l'arc avec le vecteur d'accélération afin de mieux comprendre comment ce vecteur est lié au mouvement dans le plan et dans l'espace. Rappelons que le vecteur tangente unitaire\(\vecs T\) et le vecteur normal unitaire\(\vecs N\) forment un plan osculant en tout point\(P\) de la courbe définie par une fonction à valeur vectorielle\(\vecs{r}(t)\). Le théorème suivant montre que le vecteur d'accélération\(\vecs{a}(t)\) se trouve dans le plan osculant et peut être écrit comme une combinaison linéaire de la tangente unitaire et des vecteurs normaux unitaires.
Le vecteur\(\vecs{a}(t)\) d'accélération d'un objet se déplaçant le long d'une courbe tracée par une fonction deux fois différenciable\(\vecs{r}(t)\) se trouve dans le plan formé par le vecteur tangent unitaire\(\vecs T(t)\) et le vecteur normal unitaire principal\(\vecs N(t)\) to\(C\). En outre,
\[\vecs{a}(t) = v'(t)\vecs{T}(t) + [v(t)]^2 \kappa \vecs{N}(t) \nonumber \]
\(v(t) = \|\vecs v(t)\|\)Voici la vitesse de l'\(\kappa\)objet et la courbure\(C\) tracée par\(\vecs{r}(t)\).
Parce que\(\vecs{v}(t)=\vecs{r}′(t)\) et\(\vecs{T}(t)=\dfrac{\vecs{r}′(t)}{||\vecs{r}′(t)||}\), nous l'avons fait\(\vecs v(t)=||\vecs{r}′(t)||\vecs{T}(t)=v(t)\vecs{T}(t)\).
Maintenant, nous différencions cette équation :
\[\vecs{a}(t)=\vecs{v}′(t)=\dfrac{d}{dt}\left(v(t)\vecs{T}(t)\right)=v′(t)\vecs{T}(t)+v(t)\vecs{T}′(t) \nonumber \]
Puisque\(\vecs{N}(t)=\dfrac{\vecs{T}′(t)}{||\vecs{T}′(t)||}\), nous le savons\(\vecs{T}′(t)=||\vecs{T}′(t)||\vecs{N}(t)\), donc
\[\vecs{a}(t)=v′(t)\vecs{T}(t)+v(t)||\vecs{T}′(t)||\vecs{N}(t). \nonumber \]
Une formule pour la courbure est\(\kappa=\dfrac{||\vecs{T}'(t)||}{||\vecs{r}'(t)||}\) donc\(\vecs{T}'(t) = \kappa ||\vecs{r}'(t) || = \kappa v(t) \).
Cela donne\(\vecs{a}(t)=v′(t)\vecs{T}(t)+\kappa (v(t))^2 \vecs{N}(t).\)
\(\square\)
Les coefficients de\(\vecs{T}(t)\) et\(\vecs{N}(t)\) sont appelés la composante tangentielle de l'accélération et la composante normale de l'accélération, respectivement. Nous écrivons\(a_\vecs{T}\) pour désigner la composante tangentielle et\(a_\vecs{N}\) pour désigner la composante normale.
\(\vecs{r}(t)\)Soit une fonction à valeur vectorielle qui indique la position d'un objet en fonction du temps. Puis\(\vecs{a}(t)=\vecs{r}′′(t)\) est le vecteur d'accélération. Les composantes tangentielle et normale de l'accélération\(a_\vecs{T}\) et\(a_\vecs{N}\) sont données par les formules
\[a_{\vecs{T}}=\vecs a \cdot\vecs{T}=\dfrac{\vecs{v}\cdot\vecs{a}}{||\vecs{v}||} \label{Eq1B} \]
et
\[a_\vecs{N}=\vecs a\cdot \vecs N=\dfrac{||\vecs v \times \vecs a||}{||\vecs v||}=\sqrt{||\vecs a||^2−{\left(a_{\vecs{T}}\right)^2}}. \label{Eq2B} \]
Ces composants sont liés par la formule
\[\vecs{a}(t)=a_\vecs{T} \vecs{T}(t)+a_\vecs{N}\vecs{N}(t). \label{Eq3B} \]
\(\vecs{T}(t)\)Voici le vecteur tangent unitaire à la courbe définie par\(\vecs{r}(t)\), et\(\vecs{N}(t)\) est le vecteur normal unitaire de la courbe définie par\(\vecs{r}(t)\).
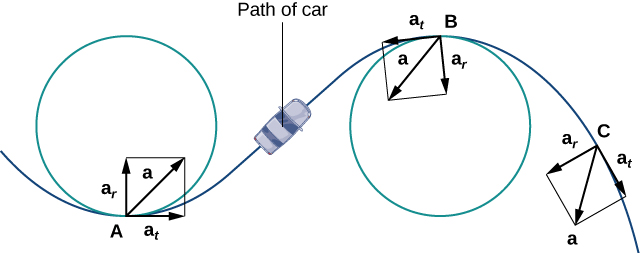
La composante normale de l'accélération est également appelée composante centripète de l'accélération ou parfois composante radiale de l'accélération. Pour comprendre l'accélération centripète, supposons que vous vous déplacez en voiture sur une piste circulaire à vitesse constante. Ensuite, comme nous l'avons vu précédemment, le vecteur d'accélération pointe à tout moment vers le centre de la piste. En tant que pilote, vous ressentez une attirance vers l'extérieur de la piste parce que vous tournez constamment. Cette sensation agit dans le sens opposé de l'accélération centripète. Il en va de même pour les tracés non circulaires. La raison en est que votre corps a tendance à se déplacer en ligne droite et résiste à la force résultant de l'accélération qui le pousse vers le côté. Notez qu'au point de\(B\) la figure,\(\PageIndex{4}\) le vecteur d'accélération pointe vers l'arrière. Cela est dû au fait que la voiture décélère lorsqu'elle entre dans la courbe.
Les vecteurs unitaires tangentiels et normaux à un point donné de la courbe fournissent un cadre de référence à ce point. Les composantes tangentielle et normale de l'accélération sont les projections du vecteur d'accélération sur\(\vecs T\) et\(\vecs N\), respectivement.
Une particule se déplace sur une trajectoire définie par la fonction à valeur vectorielle\(\vecs{r}(t)=t^2\,\hat{\mathbf i}+(2t−3)\,\hat{\mathbf j}+(3t^2−3t)\,\hat{\mathbf k}\), qui\(t\) mesure le temps en secondes et la distance en pieds.
- Recherchez\(a_\vecs{T}\) et\(a_\vecs{N}\) en tant que fonctions de\(t\).
- Trouvez\(a_\vecs{T}\) et\(a_\vecs{N}\) à l'heure\(t=2\).
Solution
- Commençons par dériver les fonctions de vitesse et d'accélération :
\[\begin{align*} \vecs{v}(t) &= \vecs{r}'(t) \\[4pt] &= 2t\,\hat{\mathbf i}+2\,\hat{\mathbf j}+(6t-3)\,\hat{\mathbf k} \\[4pt] \vecs{a}(t) &= \vecs{v}'(t) \\[4pt] &=2\,\hat{\mathbf i}+6\,\hat{\mathbf k} \end{align*}\]Maintenant, nous appliquons l'équation \ ref {Eq1B} : Nous pouvons\[\begin{align*}a_{\vecs{T}} &=\dfrac{\vecs{v}\cdot \vecs{a}}{||\vecs{v} ||} \\[4pt] &= \dfrac{ (2t \,\hat{\mathbf i} +2\,\hat{\mathbf j} +(6t-3)\,\hat{\mathbf k})\cdot(2\,\hat{\mathbf i}+6\,\hat{\mathbf k}) }{|| 2t\,\hat{\mathbf i} + 2\,\hat{\mathbf j} + (6t-3)\,\hat{\mathbf k} ||} \\[4pt] &= \dfrac{4t + 6(6t-3)}{\sqrt{(2t)^2 +2^2 + (6t-3)^2}} \\[4pt] &= \dfrac{40t-18}{40t^2 - 36t+13} \end{align*}\] maintenant appliquer l'équation \ ref {Eq2B} :
\[\begin{align*} a_\vecs{N} &=\sqrt{||\vecs{a}||^2-\left(a_{\vecs{T}}\right)^2} \\[4pt] &= \sqrt{||2\,\hat{\mathbf i}+6\,\hat{\mathbf k}||^2 - \left( \dfrac{ 40t-18 }{\sqrt{40t^2-36t+13}} \right)^2} \\[4pt] &= \sqrt{ 4+36-\dfrac{(40t-18)^2}{40t^2-36t+13} } \\[4pt] &= \sqrt{\dfrac{ 40(40t^2-36t+13)-(1600t^2-1440t+324) }{40t^2-36t+13} } \\[4pt] &= \sqrt{ \dfrac{196}{ 40t^2-36t+13} } \\[4pt] &= \dfrac{14}{\sqrt{40t^2-36t+13}} \end{align*}\]
- Nous devons évaluer chacune des réponses de la partie a à\(t=2\) :
\[\begin{align*} a_{\vecs{T}}(2) &= \dfrac{ 40(2)-18 }{\sqrt{40(2)^2 - 36(2)+13 }} \\[4pt] &= \dfrac{80-18 }{\sqrt{160-72+13}} \\[4pt] &= \dfrac{62}{\sqrt{101}} \\[4pt] a_{\vecs{N}}(2) &= \dfrac{14}{\sqrt{40(2)^2 -36(2)+13 }} \\[4pt] &= \dfrac{14}{\sqrt{160-72+13}} = \dfrac{14}{\sqrt{101}}. \end{align*}\]
Les unités d'accélération sont les pieds par seconde au carré, tout comme les unités des composantes normale et tangentielle de l'accélération.
Un objet se déplace sur une trajectoire définie par la fonction à valeur vectorielle\(\vecs r(t)=4t\,\hat{\mathbf i}+t^2\,\hat{\mathbf j}\), qui\(t\) mesure le temps en secondes.
- Recherchez\(a_\vecs{T}\) et\(a_\vecs{N}\) en tant que fonctions de\(t\).
- Trouvez\(a_\vecs{T}\) et\(a_\vecs{N}\) à l'heure\(t=−3\).
- Allusion
-
Utilisez les équations \ ref {Eq1B} et \ ref {Eq2B}
- Réponse
-
un.\[\begin{align*} a_\vecs{T} =\dfrac{\vecs v(t) \cdot \vecs a(t)}{||\vecs v(t)||}= \dfrac{\vecs r'(t) \cdot \vecs r''(t) }{||\vecs r'(t)||} \\ = \dfrac{ (4\,\hat{\mathbf i} + 2t \,\hat{\mathbf j}) \cdot (2\,\hat{\mathbf j}) }{||4\,\hat{\mathbf i} + 2t \,\hat{\mathbf j} ||} \\ = \dfrac{4t}{\sqrt{4^2 + (2t)^2}}\\ = \dfrac{2t}{\sqrt{2+t^2}} \end{align*}\]
\[\begin{align*} a_\vecs{N} = \sqrt{||\vecs a||^2-a_\vecs{T}^2}\\ =\sqrt{||2\,\hat{\mathbf j} ||^2 - \left(\dfrac{2t}{\sqrt{2+t^2}}\right)^2} \\ =\sqrt{ 4 - \dfrac{4t^2 }{2+t^2} } \end{align*}\]b.\[\begin{align*} a_\vecs{T}(−3) = \dfrac{2(-3)}{\sqrt{2+(-3)^2}} \\ = \dfrac{-6}{\sqrt{11}}\end{align*}\]
\[\begin{align*}a_\vecs{N}(−3) = \sqrt{ 4 - \dfrac{4(-3)^2 }{2+(-3)^2} } \\ = \sqrt{4- \dfrac{36}{11}} \\ = \sqrt{\dfrac{8}{11} }\\ =\dfrac{2\sqrt{2}}{\sqrt{11}} \end{align*}\]
Mouvement du projectile
Regardons maintenant une application de fonctions vectorielles. Examinons en particulier l'effet de la gravité sur le mouvement d'un objet lorsqu'il se déplace dans l'air et la façon dont elle détermine la trajectoire résultante de cet objet. Dans ce qui suit, nous ignorons l'effet de la résistance à l'air. Cette situation, dans laquelle un objet se déplace à une vitesse initiale mais où aucune force n'agit sur lui autre que la gravité, est connue sous le nom de mouvement du projectile. Il décrit le mouvement d'objets, des balles de golf aux balles de baseball, et des flèches aux boulets de canon.
Nous devons d'abord choisir un système de coordonnées. Si nous nous trouvons à l'origine de ce système de coordonnées, nous choisissons l'\(y\)axe positif vers le haut, l'axe négatif\(y\) vers le bas et l'axe positif\(x\) vers l'avant (c'est-à-dire éloigné du lanceur de l'objet). L'effet de la gravité se fait vers le bas, de sorte que la deuxième loi de Newton nous indique que la force sur l'objet résultant de la gravité est égale à la masse de l'objet multipliée par l'accélération résultant de la gravité\(\vecs F_g=m\vecs a\), ou, où\(\vecs F_g\) représente la force de gravité et\(\vecs a = -g\,\hat{\mathbf j}\) représente accélération résultant de la gravité à la surface de la Terre. La valeur de\(g\) dans le système de mesure anglais est d'environ 32 pieds/sec 2 et elle est d'environ 9,8 m/sec 2 dans le système métrique. C'est la seule force agissant sur l'objet. Puisque la gravité agit dans une direction descendante, nous pouvons écrire la force résultant de la gravité dans la forme\(\vecs F_g=−mg\,\hat{\mathbf j}\), comme indiqué sur la figure\(\PageIndex{5}\).
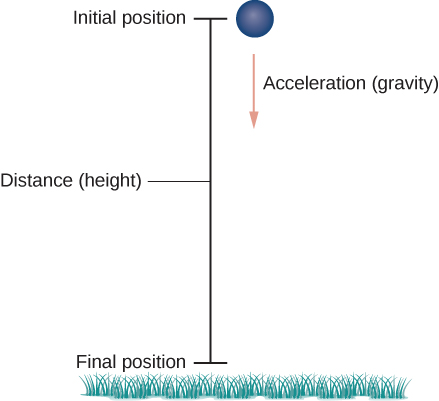
La deuxième loi de Newton nous indique également que\(F=m\vecs{a}\), où\(\vecs a\) représente le vecteur d'accélération de l'objet. Cette force doit être égale à la force de gravité à tout moment, nous savons donc que
\[\begin{align*} \vecs F =\vecs F_g \\ m\vecs{a} = -mg \,\hat{\mathbf j} \\ \vecs{a} = -g\,\hat{\mathbf j}. \end{align*}\]
Nous utilisons maintenant le fait que le vecteur d'accélération est la dérivée première du vecteur de vitesse. Par conséquent, nous pouvons réécrire la dernière équation sous la forme
\[\vecs v'(t) = -g\,\hat{\mathbf j} \nonumber \]
En prenant l'antidérivée de chaque côté de cette équation, nous obtenons
\[ \vecs v(t) = \int -g \,\hat{\mathbf j}\; dt = -gt\,\hat{\mathbf j} + \vecs C_1 \nonumber \]
pour un vecteur constant\(\vecs C_1\). Pour déterminer la valeur de ce vecteur, nous pouvons utiliser la vitesse de l'objet à un moment fixe, par exemple à un moment donné\(t=0\). Nous appelons cette vitesse la vitesse initiale :\(\vecs v(0)=\vecs v_0\). Donc,\(\vecs v(0)=−g(0)\,\hat{\mathbf j}+\vecs C_1=\vecs v_0\) et\(\vecs C_1= \vecs v_0\). Cela donne le vecteur de vitesse comme\(\vecs v(t)=−gt\,\hat{\mathbf j}+\vecs v_0\).
Ensuite, nous utilisons le fait que la vitesse\(\vecs{v}(t)\) est la dérivée de la position\(\vecs{s}(t)\). Cela donne l'équation
\[\vecs s'(t)=-gt\,\hat{\mathbf j}+\vecs{v}_0. \nonumber \]
La prise de l'antidérivée des deux côtés de cette équation conduit à
\[\begin{align*} \vecs s(t) &= \int -gt\,\hat{\mathbf j} + \vecs{v}_0 \;dt \\[4pt] &= -\dfrac{1}{2}gt^2 \,\hat{\mathbf j} + \vecs{v}_0 t + \vecs{C}_2 \end{align*}\]
avec un autre vecteur constant inconnu\(\vecs{C}_2\). Pour déterminer la valeur de\(\vecs{C}_2\), nous pouvons utiliser la position de l'objet à un moment donné, disons à un moment donné\(t=0\). Nous appelons cette position la position initiale :\(\vecs{s}(0)=\vecs{s}_0\). Par conséquent,\(\vecs{s}(0)=−(1/2)g(0)^2\,\hat{\mathbf j}+\vecs{v}_0(0)+\vecs{C}_2=\vecs{s}_0\). Cela donne la position de l'objet à tout moment comme
\[ \vecs{s}(t)=−\dfrac{1}{2}gt^2 \,\hat{\mathbf j}+\vecs{v}_0 t+\vecs{s}_0. \nonumber \]
Examinons de plus près la vitesse initiale et la position initiale. Supposons en particulier que l'objet soit projeté vers le haut depuis l'origine selon un angle par rapport\(\theta\) à l'horizontale, avec une vitesse initiale\(\vecs{v}_0\). Comment modifier le résultat précédent pour refléter ce scénario ? Tout d'abord, on peut supposer qu'il est jeté depuis l'origine. Si ce n'est pas le cas, nous pouvons déplacer l'origine jusqu'au point d'où elle est lancée. Par conséquent\(\vecs{s}_0=\vecs{0}\), comme le montre la figure\(\PageIndex{6}\).
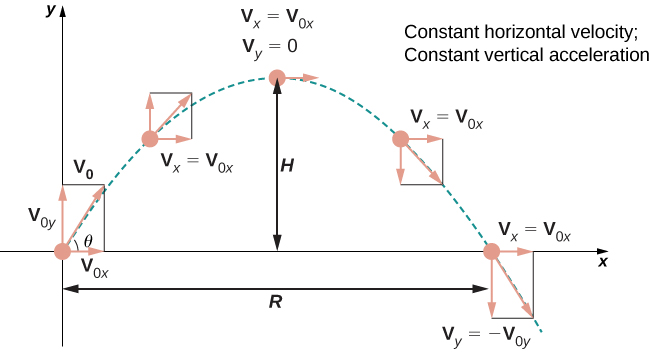
Nous pouvons réécrire le vecteur de vitesse initial dans le formulaire\(\vecs{v}_0= v_0 \cos \theta \,\hat{\mathbf i} + v_0 \sin \theta \,\hat{\mathbf j}\). Ensuite, l'équation de la fonction de position\(\vecs{s}(t)\) devient
\[\begin{align*} \vecs{s}(t) &=-\dfrac{1}{2} gt^2\,\hat{\mathbf j} + v_0 t \cos\theta \,\hat{\mathbf i} + v_0 t \sin\theta \,\hat{\mathbf j} \\[4pt] &= v_0 t \cos\theta\,\hat{\mathbf i} + v_0 t \sin\theta \,\hat{\mathbf j} - \dfrac{1}{2} gt^2\,\hat{\mathbf j} \\[4pt] &= v_0 t \cos\theta \,\hat{\mathbf i} + \left(v_0 t \sin\theta - \dfrac{1}{2} gt^2\right)\,\hat{\mathbf j}. \end{align*}\]
Le coefficient de\(\hat{\mathbf i}\) représente la composante horizontale de\(\vecs{s}(t)\) et est la distance horizontale de l'objet par rapport à l'origine à un moment donné\(t\). La valeur maximale de la distance horizontale (mesurée aux mêmes altitudes initiale et finale) est appelée distance\(R\). Le coefficient de\(\hat{\mathbf j}\) représente la composante verticale\(\vecs{s}(t)\) et est l'altitude de l'objet à un moment donné\(t\). La valeur maximale de la distance verticale est la hauteur\(H\).
Lors d'une célébration de la fête de l'indépendance, un boulet de canon est tiré d'un canon sur une falaise en direction de l'eau. Le canon est dirigé à un angle de 30° au-dessus de l'horizontale et la vitesse initiale du boulet de canon est de 600 pieds/sec. La falaise se trouve à 100 pieds au-dessus de l'eau (Figure\(\PageIndex{7}\)).
- Détermine la hauteur maximale du boulet de canon.
- Combien de temps faudra-t-il pour que le boulet de canon se jette dans la mer ?
- À quelle distance de la mer le boulet de canon va-t-il toucher l'eau ?
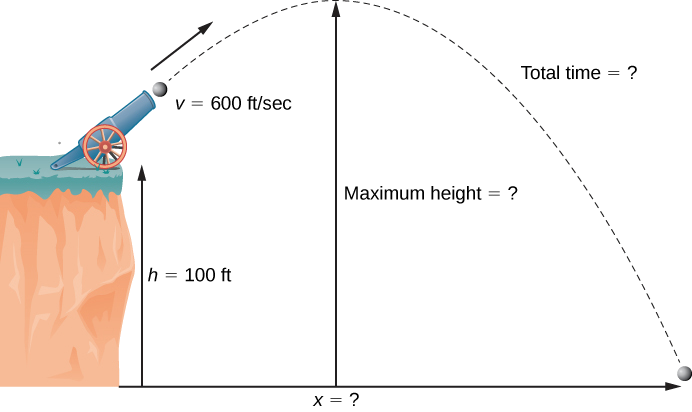
Solution
Nous utilisons l'équation
\[\vecs{s}(t) = v_0 t \cos\theta \,\hat{\mathbf i} + \left(v_0 t \sin\theta - \dfrac{1}{2}gt^2 \right)\,\hat{\mathbf j} \nonumber \]
avec\(\theta=30^\circ \)\(g=32 \dfrac{\text{ft}}{\text{sec}^2}\), et\(v_0=600 \dfrac{\text{ft}}{\text{sec}^2}\). Ensuite, l'équation de position devient
\[\begin{align*} \vecs{s}(t) &= 600 t ( \cos 30^\circ)\,\hat{\mathbf i} + \left(600t \sin30^\circ - \dfrac{1}{2}(32)t^2 \right)\,\hat{\mathbf j} \\[4pt] &= 300t\sqrt{3} \,\hat{\mathbf i} + \left( 300t - 16t^2 \right)\,\hat{\mathbf j} \end{align*}\]
- Le boulet atteint sa hauteur maximale lorsque la composante verticale de sa vitesse est nulle, car le boulet ne monte ni ne descend à ce point. Le vecteur de vitesse est
\[\begin{align*} \vecs{v}(t) &=\vecs s'(t)\\[4pt] &= 300 \sqrt{3} \,\hat{\mathbf i} + (300-32t)\,\hat{\mathbf j} \end{align*} \nonumber \]
Par conséquent, la composante verticale de la vitesse est donnée par l'expression\(300−32t\). La définition de cette expression à zéro et la résolution de t donnent la valeur\(t=9.375\) sec. La hauteur du boulet de canon à ce moment est donnée par la composante verticale du vecteur de position, évaluée à\(t=9.375\).\[\begin{align*} \vecs{s}(9.375) &=300(9.375)\sqrt{3}\,\hat{\mathbf i}+(300(9.375)−16(9.375)^2)\,\hat{\mathbf j} \\[4pt] &=4871.39 \,\hat{\mathbf i}+1406.25\,\hat{\mathbf j} \end{align*}\]
Par conséquent, la hauteur maximale du boulet de canon est de 1406,39 pieds au-dessus du canon, soit 1506,39 pieds au-dessus du niveau de la mer. - Lorsque le boulet de canon atterrit dans l'eau, il se trouve à 100 pieds sous le canon. La composante verticale du vecteur de position est donc égale à -100. En fixant la composante verticale\(\vecs s(t)\) égale à −100 et en résolvant, on obtient
\[\begin{align*} 300t-16t^2 &= -100 \\ 16t^2-300t-100 =0 \\4t^2-75-25 =0 \\[4pt] t &= \dfrac{75\pm \sqrt{(-75)^2}-4(4)(-25) }{2(4)} \\[4pt] &= \dfrac{75 \pm \sqrt{6025}}{8} \\[4pt] &= \dfrac{75 \pm 5\sqrt{241}}{8} \end{align*}\]
La valeur positive\(t\) qui résout cette équation est d'environ 19,08. Par conséquent, le boulet de canon entre en contact avec l'eau après environ 19,08 secondes. - Pour connaître la distance jusqu'à la mer, il suffit de remplacer la réponse de la partie (b) par\(\vecs{s}(t)\) :
\[\begin{align*} \vecs s(19.08) &=300(19.08)\sqrt{3} \,\hat{\mathbf i}+\left(300(19.08)−16(19.08)^2\right)\,\hat{\mathbf j}\\[4pt] &=9914.26\,\hat{\mathbf i}−100.7424\,\hat{\mathbf j} \end{align*}\]
La balle touche donc l'eau à environ 9914,26 pieds de la base de la falaise. Notez que la composante verticale du vecteur de position est très proche de −100, ce qui indique que la balle vient de toucher l'eau. Notez que 9914,26 pieds n'est pas la portée réelle du canon puisque le boulet de canon atterrit dans l'océan à un endroit situé sous le canon. La portée du canon serait déterminée en déterminant la distance à laquelle se trouve le boulet lorsque sa hauteur est de 100 pieds au-dessus de l'eau (la même que l'altitude du canon).
Un archer tire une flèche à un angle de 40° au-dessus de l'horizontale avec une vitesse initiale de 98 m/sec. La hauteur de l'archer est de 171,5 cm. Déterminez la distance horizontale parcourue par la flèche avant qu'elle ne touche le sol.
- Allusion
-
L'équation du vecteur de position doit tenir compte de la hauteur de l'archer en mètres.
- Réponse
-
967,15 km
Une dernière question demeure : en général, quelle est la distance maximale qu'un projectile peut parcourir, compte tenu de sa vitesse initiale ? Pour déterminer cette distance, nous supposons que le projectile est tiré depuis le sol et que nous souhaitons qu'il revienne au niveau du sol. En d'autres termes, nous voulons déterminer une équation pour la plage. Dans ce cas, l'équation du mouvement du projectile est
\[\vecs{s}=v_0 t \cos\theta \,\hat{\mathbf i} + \left(v_0t\sin\theta - \dfrac{1}{2}gt^2 \right)\,\hat{\mathbf j}. \nonumber \]
Fixer la deuxième composante à zéro et résoudre les problèmes liés aux\(t\) rendements
\[\begin{align*} v_0 t \sin\theta - \dfrac{1}{2}gt^2 =0\\ t\left(v_0 \sin\theta - \dfrac{1}{2}gt\right) =0 \end{align*}\]
Donc,\(t=0\) soit\(t=\dfrac{2v_0\sin\theta}{g}\). Nous sommes intéressés par la deuxième valeur de\(t\), nous la substituons donc par\(\vecs{s}(t)\), ce qui donne
\[\begin{align*} \vecs{s}\left(\dfrac{2v_0\sin\theta}{g} \right) = v_0 \left(\dfrac{2v_0\sin\theta}{g} \right) \cos\theta \,\hat{\mathbf i} + \left( v_0\left(\dfrac{2v_0\sin\theta}{g} \right)\sin\theta - \dfrac{1}{2}g\left(\dfrac{2v_0\sin\theta}{g} \right)^2 \right)\,\hat{\mathbf j} \\ = \left(\dfrac{2v_0^2\sin\theta\cos\theta}{g} \right)\,\hat{\mathbf i} \\ = \dfrac{v_0^2 \sin2\theta}{g}\,\hat{\mathbf i}. \end{align*}\]
Ainsi, l'expression de la portée d'un projectile tiré à un angle\(\theta\) est
\[R=\dfrac{v_0^2 \sin2\theta}{g}\,\hat{\mathbf i} . \nonumber \]
La seule variable de cette expression est\( \theta\). Pour maximiser la distance parcourue, prenez la dérivée du coefficient de i par rapport à zéro :\(\theta\)
\[\begin{align*} \dfrac{d}{d\theta} \left( \dfrac{v_0^2 \sin2\theta}{g} \right) =0\\ \dfrac{2v_0^2\cos2\theta}{g} =0\\ \theta=45^\circ \end{align*}\]
Cette valeur de\(\theta)\) est la plus petite valeur positive qui rend la dérivée égale à zéro. Par conséquent, en l'absence de résistance de l'air, le meilleur angle pour tirer un projectile (afin de maximiser la portée) est un angle de 45°. La distance parcourue est donnée par
\[\vecs{s}\left(\dfrac{2v_0 \sin 45^\circ}{g} \right)= \dfrac{v_0^2 \sin 90^\circ}{g} \,\hat{\mathbf i} = \dfrac{v_0^2}{g}\,\hat{\mathbf i} \nonumber \]
Par conséquent, la plage pour un angle de 45° est exprimée en\(\frac{v_0^2}{g}\) unités.
Les lois de Kepler
Au début des années 1600, Johannes Kepler a pu utiliser les données incroyablement précises de son mentor Tycho Brahe pour formuler ses trois lois du mouvement planétaire, désormais connues sous le nom de lois du mouvement planétaire de Kepler. Ces lois s'appliquent également à d'autres objets du système solaire en orbite autour du Soleil, tels que les comètes (par exemple, la comète de Halley) et les astéroïdes. Des variantes de ces lois s'appliquent aux satellites en orbite autour de la Terre.
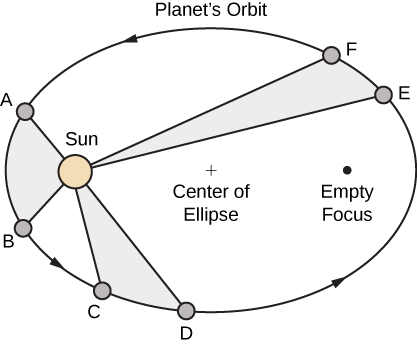
- La trajectoire de toute planète autour du Soleil est de forme elliptique, le centre du Soleil étant situé à l'un des foyers de l'ellipse (la loi des ellipses).
- Une ligne tracée du centre du Soleil au centre d'une planète balaie des zones égales à intervalles de temps égaux (la loi des surfaces égales) (Figure\(\PageIndex{8}\)).
- Le rapport des carrés des périodes de deux planètes est égal au rapport des cubes des longueurs de leurs demi-grands axes orbitaux (la loi des harmonies).
La troisième loi de Kepler est particulièrement utile lorsque l'on utilise des unités appropriées. En particulier, 1 unité astronomique est définie comme étant la distance moyenne entre la Terre et le Soleil, et elle est maintenant reconnue comme étant de 149 597 870 700 m, soit environ 93 000 000 miles. Nous écrivons donc 1 UA = 93 000 000 mi. Comme le temps nécessaire à la Terre pour orbiter autour du Soleil est d'un an, nous utilisons les années terrestres pour les unités de temps. Ensuite, en substituant 1 an à la période de la Terre et 1 UA à la distance moyenne par rapport au Soleil, la troisième loi de Kepler peut être écrite comme
\[ T_p^2=D_p^3 \nonumber \]
pour toute planète du système solaire, où\(T_P\) est la période de cette planète mesurée en années terrestres et\(D_P\) la distance moyenne entre cette planète et le Soleil mesurée en unités astronomiques. Par conséquent, si nous connaissons la distance moyenne entre une planète et le Soleil (en unités astronomiques), nous pouvons alors calculer la durée de son année (en années terrestres), et vice versa.
Les lois de Kepler ont été formulées sur la base des observations de Brahe ; cependant, elles n'ont été formellement prouvées que lorsque Sir Isaac Newton a pu appliquer le calcul. De plus, Newton a pu généraliser la troisième loi de Kepler à d'autres systèmes orbitaux, tels qu'une lune orbitant autour d'une planète. La troisième loi originale de Kepler ne s'applique qu'aux objets en orbite autour du Soleil.
Prouvons maintenant la première loi de Kepler en utilisant le calcul de fonctions à valeur vectorielle. Nous avons d'abord besoin d'un système de coordonnées. Placons le Soleil à l'origine du système de coordonnées et laissons la fonction à valeur vectorielle\(\vecs{r}(t)\) représenter la position d'une planète en fonction du temps. Newton a prouvé la loi de Kepler en utilisant sa deuxième loi du mouvement et sa loi de gravitation universelle. La deuxième loi du mouvement de Newton peut être écrite comme\(\vecs{F}=m\vecs{a}\), où\(\vecs{F}\) représente la force nette agissant sur la planète. Sa loi de gravitation universelle peut être écrite sous cette forme\(\vecs{F}=−\dfrac{GmM}{||\vecs{r}||^2}\cdot \dfrac{\vecs{r}}{||\vecs{r} ||}\), qui indique que la force résultant de l'attraction gravitationnelle du Soleil pointe vers le Soleil et a une amplitude\(\dfrac{GmM}{||\vecs{r}||^2} \) (Figure\(\PageIndex{9}\)).
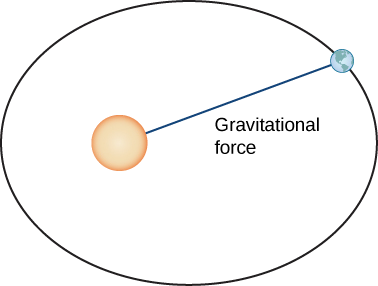
En mettant ces deux forces égales l'une à l'autre, et en utilisant le fait que\(\vecs a(t)=\vecs v′(t)\), nous obtenons
\[ m\vecs v′(t)=−\frac{GmM}{‖\vecs r‖^2}⋅\frac{\vecs r}{‖\vecs r‖}, \nonumber \]
qui peut être réécrit comme
\[ \dfrac{d\vecs v}{dt}=−\dfrac{GM}{||\vecs r||^3}\vecs{r}. \nonumber \]
Cette équation montre que les vecteurs\(d\vecs{v}/dt\) et\(\vecs r\) sont parallèles les uns aux autres, donc\(d\vecs {v}/dt \times \vecs {r}=\vecs 0\). Ensuite, différencions\(\vecs{r} \times \vecs{v}\) par rapport au temps :
\[\dfrac{d}{dt}(\vecs{r}\times \vecs{v})=\dfrac{d\vecs{r}}{dt}\times \vecs v+\vecs{r} \times \dfrac{d\vecs{v}}{dt}=\vecs{v}\times \vecs{v}+\vecs{0}=\vecs{0}. \label{Eq10} \]
Cela prouve qu'il s'\(\vecs{r}\times\vecs{v}\)agit d'un vecteur constant, que nous appelons\(\vecs C\). Puisque\(\vecs r\) et\(\vecs v\) sont tous deux perpendiculaires\(\vecs C\) à toutes les valeurs de\(t\), ils doivent se trouver dans un plan perpendiculaire à\(\vecs C\). Par conséquent, le mouvement de la planète se situe dans un plan.
Ensuite, nous calculons l'expression\(d\vecs{v}/dt\times \vecs C\) :
\[\dfrac{d\vecs{v}}{dt} \times \vecs{C}=−\dfrac{GM}{||\vecs{r}||^3}\vecs{r}\times (\vecs{r}\times\vecs{v})=−\dfrac{GM}{||\vecs r||^3}[(\vecs{r} \cdot \vecs{v})\vecs{r} - (\vecs{r} \cdot \vecs{r})\vecs{v}]. \label{Eq11} \]
La dernière égalité dans l'équation \ ref {Eq10} provient de la formule du triple produit croisé (Introduction aux vecteurs dans l'espace). Nous avons besoin d'une expression pour\(\vecs{r}\cdot \vecs{v}\). Pour le calculer, nous différencions\(\vecs{r}\cdot \vecs{r}\) par rapport au temps :
\[ \dfrac{d}{dt}(\vecs{r}\cdot \vecs{r})=\dfrac{d\vecs{r}}{dt}\cdot \vecs{r}+\vecs{r}\cdot \dfrac{d\vecs{r}}{dt}=2\vecs{r}\cdot \dfrac{d\vecs{r}}{dt}=2\vecs{r}\cdot \vecs{v}. \label{Eq12} \]
Depuis\(\vecs{r}\cdot\vecs{r}=||\vecs r||^2\), nous avons également
\[\dfrac{d}{dt}(\vecs{r}\cdot \vecs{r})=\dfrac{d}{dt}||\vecs{r}||^2=2||\vecs{r}|| \dfrac{d}{dt}||\vecs{r}||. \label{Eq13} \]
En combinant l'équation \ ref {Eq12} et l'équation \ ref {Eq13}, nous obtenons
\[\begin{align*} 2\vecs{r}\cdot \vecs{v} =2||\vecs{r}||\dfrac{d}{dt}||\vecs{r}|| \\ \vecs{r} \cdot \vecs{v} =||\vecs{r}‖\dfrac{d}{dt}||\vecs{r}||. \end{align*} \label{Eq14} \]
La substitution de ceci dans l'équation \ ref {Eq11} nous donne
\[\begin{align} \dfrac{d\vecs{v}}{dt} \times \vecs{C} = - \dfrac{GM}{||\vecs{r}||^3} [(\vecs{r}\cdot \vecs{v})\vecs{r} - (\vecs{r}\cdot \vecs{r})\vecs{v}] \nonumber \\ = -\dfrac{GM}{||\vecs{r}||^3}\left[ ||\vecs{r} \left(\dfrac{d}{dt} ||\vecs{r}||\right)\vecs{r} - ||\vecs{r}||^2\vecs{v} \right] \nonumber \\ = -GM\left[ \dfrac{1}{||\vecs{r}||^2}\left( \dfrac{d}{dt} ||\vecs{r}|| \right)\vecs{r} - \dfrac{1}{||\vecs{r}||}\vecs{v} \right] \nonumber \\ = GM\left[ \dfrac{\vecs{v}}{||\vecs{r}||} -\dfrac{\vecs{r}}{||\vecs{r}||^2}\left( \dfrac{d}{dt} ||\vecs{r}|| \right) \right]. \label{Eq15} \end{align} \]
Toutefois,
\[ \begin{align*} \dfrac{d}{dt} \dfrac{\vecs{r}}{||\vecs{r}||} = \dfrac{ \frac{d}{dt}(\vecs{r})||\vecs{r}||- \vecs{r}\frac{d}{dt}||\vecs{r}|| }{||\vecs{r}||^2} \\ = \dfrac{ \frac{d\vecs{r}}{dt} }{||\vecs{r}||} - \dfrac{\vecs{r}}{||\vecs{r}||^2}\dfrac{d}{dt}||\vecs{r} || \\ = \dfrac{\vecs{v}}{||\vecs{r}||} - \dfrac{\vecs{r}}{||\vecs{r}||^2} \dfrac{d}{dt}||\vecs{r}||. \end{align*}\]
Par conséquent, l'équation \ ref {Eq15} devient
\[\dfrac{d \vecs{v}}{dt}\times \vecs{C}=GM\left( \dfrac{d}{dt}\dfrac{ \vecs{r}}{ || \vecs{r} ||} \right).\nonumber \]
Comme\(\vecs{C}\) il s'agit d'un vecteur constant, nous pouvons intégrer les deux côtés et obtenir
\[ \vecs{v}\times\vecs{C} = GM \dfrac{ \vecs{r} }{|| \vecs{r} ||} + \vecs{D}, \nonumber \]
où\(\vecs D\) est un vecteur constant. Notre objectif est de résoudre\(|| \vecs{r} ||\). Commençons par calculer\( \vecs{r} \cdot ( \vecs{v}\times \vecs{C}\) :
\[\vecs{r} \cdot ( \vecs{v}\times \vecs{C} =GM\dfrac{||\vecs{r}||^2}{||\vecs{r}||}+ \vecs{r}\cdot\vecs{D} =GM||\vecs{r}||+\vecs{r}\cdot \vecs{D}. \nonumber \]
Cependant\( \vecs{r} \cdot ( \vecs{v}\times \vecs{C})= ( \vecs{r} \times \vecs{v})\cdot \vecs{C} \), donc
\[ ( \vecs{r} \times \vecs{v})\cdot \vecs{C} =GM||\vecs{r}|| + \vecs{r}\cdot \vecs{D}.\nonumber \]
Depuis\(\vecs{r}\times \vecs{v}=\vecs{C}\), nous avons
\[ ||\vecs{C}||^2 =GM||\vecs{r}|| +\vecs{r}\cdot \vecs{D}.\nonumber \]
Notez que\( \vecs{r} \cdot \vecs{D}=||\vecs{r}|| ||\vecs{D}||\cos \theta \), où\(\theta\) est l'angle entre\(\vecs{r}\) et\(\vecs{D}\). Par conséquent,
\[ ||\vecs{C}||^2=GM||\vecs{r}||+||\vecs{r}|| ||\vecs{D}|| \cos\theta \nonumber \]
Résoudre pour\(||\vecs{r}||\),
\[ ||\vecs{r}|| = \dfrac{||\vecs{C}||^2 }{GM+||\vecs{D}||\cos\theta} = \dfrac{||\vecs{C}||^2}{GM}\left( \dfrac{1}{1+e\cos\theta} \right). \nonumber \]
où\(e=||\vecs{D}||/GM\). Il s'agit de l'équation polaire d'une conique dont le foyer se situe à l'origine, que nous avons définie comme étant le Soleil. C'est une hyperbole si\(e>1\), une parabole si\(e=1\) ou une ellipse si\(e<1\). Puisque les planètes ont des orbites fermées, la seule possibilité est celle d'une ellipse. Cependant, à ce stade, il convient de mentionner que des comètes hyperboliques existent. Il s'agit d'objets qui ne font que traverser le système solaire à des vitesses trop élevées pour être piégés en orbite autour du Soleil. Lorsqu'ils passent suffisamment près du Soleil, le champ gravitationnel du Soleil dévie suffisamment la trajectoire pour que la trajectoire devienne hyperbolique.
\(\square\)
La troisième loi du mouvement planétaire de Kepler peut être modifiée pour le cas d'un objet en orbite autour d'un objet autre que le Soleil, comme la Lune autour de la Terre. Dans ce cas, la troisième loi de Kepler devient
\[P^2 = \dfrac{4\pi^2 a^3}{G(m+M)}, \label{Eq30} \]
où m est la masse de la Lune et M est la masse de la Terre, a représente la longueur du grand axe de l'orbite elliptique et P représente la période.
Étant donné que la masse de la Lune est de\(7.35\times 10^{22}\) kg, que la masse de la Terre est de\(5.97\times 10^{24}\) kg et que la période de la Lune est de 27,3 jours, déterminons la longueur du grand axe de l'orbite de la Lune autour de la Terre.\(G=6.67\times 10^{−11} \text{m} / \text{kg} \cdot \text{sec}^2\)
Solution
Il est important d'être cohérent avec les unités. Comme la constante gravitationnelle universelle contient les secondes dans les unités, nous devons également utiliser les secondes pour la période de la Lune :
\[27.3 \; \text{days} \times \dfrac{24 \; \text{hr}}{1 \; \text{day}} \times \dfrac{3600 \; \text{esc}}{1 \; \text{hour}} =2,358,720\; \text{sec}\nonumber \]
Remplacez toutes les données dans l'équation \ ref {Eq30} et résolvez pour\(a\) :
\[\begin{align*} (2,358,720sec)^2 = \dfrac{4\pi^2a^3}{\left( 6.67\times 10^{-11} \frac{m}{\text{kg}\times \text{sec}^2}\right) (7.35\times 10^{22}\text{kg} + 5.97 \times 10^{24}\text{kg})} \\ 5.563 \times 10^{12} = \dfrac{ 4\pi^2a^3}{(6.67 \times 10^{-11}\text{m}^3)(6.04 \times 10^{24})} \\ (5.563 \times 10^{12})(6.67 \times 10^{-11} \text{m}^3)(6.04 \times 10^{24}) = 4\pi^2 a^3 \\ a^3 = \dfrac{2.241 \times 10^{27}}{4\pi^2}\text{m}^3 \\ a = 3.84 \times 10^8 \text{m} \\ \approx 384,000 \,\text{km}. \end{align*}\]
Analyse
Selon solarsystem.nasa.gov, la distance moyenne réelle entre la Lune et la Terre est de 384 400 km. Ceci est calculé à l'aide des réflecteurs laissés sur la Lune par les astronautes d'Apollo dans les années 1960.
Titan est la plus grande lune de Saturne. La masse de Titan est d'environ\(1.35 \times 10^{23} kg\). La masse de Saturne est d'environ\( 5.68 \times 10^{26}\) kg. Titan met environ 16 jours pour orbiter autour de Saturne. Utilisez ces informations, ainsi que la constante de gravitation universelle,\(G=6.67×10^{−11} \text{m}/\text{kg} \cdot \text{sec}^2\) pour estimer la distance entre Titan et Saturne.
- Allusion
-
Assurez-vous que vos unités sont identiques, puis utilisez l'équation \ ref {Eq30}.
- Réponse
-
\[a\approx 1.224 \times 10^9 \text{m}= 1,224,000 \text{km} \nonumber \]
Nous revenons maintenant à l'ouverture du chapitre, qui traite du mouvement de la comète de Halley autour du Soleil. La première loi de Kepler stipule que la comète de Halley suit une trajectoire elliptique autour du Soleil, le Soleil étant l'un des foyers de l'ellipse. La période de la comète de Halley est d'environ 76,1 ans, selon la proximité avec laquelle elle passe par Jupiter et Saturne lorsqu'elle traverse le système solaire externe. Utilisons les\(T=76.1\) années. Quelle est la distance moyenne entre la comète de Halley et le Soleil ?

Solution
En utilisant l'équation\(T^2=D^3\) avec\(T=76.1\), nous obtenons\(D^3=5791.21\), donc\(D\approx 17.96\) A.U. Cela donne environ\(1.67\times 10^9\) mi.
Il est naturel de se poser la question suivante : quelles sont les distances maximale (aphélie) et minimale (périhélie) entre la comète de Halley et le Soleil ? L'excentricité de l'orbite de la comète de Halley est de 0,967 (Source : http://nssdc.gsfc.nasa.gov/planetary...cometfact.html). Rappelez-vous que la formule de l'excentricité d'une ellipse est\(e=c/a\) la suivante : a est la longueur du demi-grand axe et c est la distance entre le centre et l'un ou l'autre des foyers. Par conséquent,\(0.967=c/17.96\) et\(c\approx 17.37\) A.U. En soustrayant cette valeur de a, on obtient la distance du périhélie\(p=a−c=17.96−17.37=0.59\) A.U. Selon le National Space Science Data Center (Source : http://nssdc.gsfc.nasa.gov/planetary...cometfact.html), la distance du périhélie pour la comète de Halley est de 0,587 A.U. Pour calculer la distance entre aphélions, nous ajoutons
\[ P=a+c=17.96+17.37=35.33 \; \text{A.U.} \nonumber \]
C'est environ\(3.3\times 10^9\) km. La distance moyenne entre Pluton et le Soleil est de 39,5 UA (Source : http://www.oarval.org/furthest.htm), il semblerait donc que la comète de Halley reste juste sur l'orbite de Pluton.
À quelle vitesse une voiture de course peut-elle effectuer un virage circulaire sans déraper et heurter le mur ? La réponse peut dépendre de plusieurs facteurs :
- Le poids de la voiture ;
- La friction entre les pneus et la route ;
- Le rayon du cercle ;
- La « raideur » du virage.
Dans ce projet, nous étudions cette question pour les voitures de course NASCAR sur le Bristol Motor Speedway dans le Tennessee. Avant d'aborder cette piste en particulier, nous utilisons des fonctions vectorielles pour développer les mathématiques et la physique nécessaires pour répondre à de telles questions.
Une voiture massive\(m\) se déplace à vitesse angulaire constante\(\omega\) autour d'une courbe circulaire de rayon\(R\) (Figure\(\PageIndex{9}\)). La courbe est inclinée selon un angle\(\theta\). Si la hauteur de la voiture par rapport au sol est\(h\), la position de la voiture à ce moment\(t\) est donnée par la fonction\(\vecs r(t)=< R\cos(\omega t),R\sin(\omega t),h>\).

- Trouvez la fonction\(\vecs{v}(t)\) de vitesse de la voiture. Montre qui\(\vecs{v}\) est tangente à la courbe circulaire. Cela signifie que, sans force pour maintenir la voiture dans la courbe, la voiture en sortira.
- Montrez que la vitesse de la voiture est\(\omega R\). Utilisez ceci pour le montrer\((2\pi 4)/\|\vecs{v}\|=(2\pi)/\omega \).
- Trouvez l'accélération\(\vecs{a}\). Montrez que ce vecteur pointe vers le centre du cercle et que\(\|\vecs{a}\|=R\omega ^2\).
- La force requise pour produire ce mouvement circulaire est appelée force centripète, et elle est désignée\( \vecs{F}_{cent} \). Cette force pointe vers le centre du cercle (et non vers le sol). Montrez ça\(\|\vecs{F}_{cent}\|=\left(m|\vecs{v}|^2 \right)/R\).
Lorsque la voiture se déplace dans la courbe, trois forces agissent sur elle : la gravité, la force exercée par la route (cette force est perpendiculaire au sol) et la force de friction (Figure\(\PageIndex{10}\)). Comme il est complexe de décrire la force de frottement générée par les pneus et la route, nous utilisons une approximation standard pour la force de frottement. Supposons que\(\vecs{f}=\mu \vecs{N}\) pour une constante positive\(\mu \). La constante\(\mu\) s'appelle le coefficient de frottement.
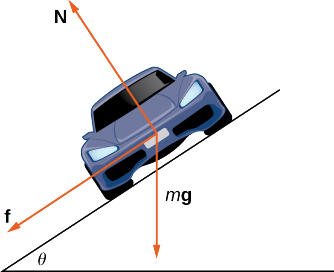
\(v_{max}\)Dénotons la vitesse maximale que la voiture peut atteindre dans la courbe sans déraper. En d'autres termes,\(v_{max}\) c'est la vitesse la plus rapide à laquelle la voiture peut effectuer le virage. Lorsque la voiture se déplace à cette vitesse, l'amplitude de la force centripète est
\[\| \vecs{F}_{cent} \| = \dfrac{m(v_{max})^2}{R}. \nonumber \]
Les trois questions suivantes portent sur l'élaboration d'une formule qui relie la vitesse\(v_{max}\) à l'angle bancaire\(\theta\).
- Montre ça\(\vecs{N} \cos\theta=m\vecs g+\vecs{f} \sin\theta\). Concluez cela\(\vecs{N}=(m\vecs g)/(\cos\theta−\mu \sin\theta)\).
- La force centripète est la somme des forces dans le sens horizontal, puisque la force centripète pointe vers le centre de la courbe circulaire. Montrez que
\[\vecs{F}_{cent}=\vecs{N} \sin\theta+\vecs{f}\cos\theta. \nonumber \]
Concluez que\[\vecs{F}_{cent}=\dfrac{\sin\theta+\mu \cos\theta}{cos\theta−\mu \sin\theta} m\vecs g. \nonumber \]
- Montre ça\((v_{\text{max}})^2=((\sin\theta+\mu\ cos\theta)/(\cos\theta−\mu \sin\theta))gR\). Concluez que la vitesse maximale ne dépend pas réellement de la masse de la voiture.
Maintenant que nous disposons d'une formule liant la vitesse maximale de la voiture et l'angle d'inclinaison, nous sommes en mesure de répondre à des questions comme celle posée au début du projet.
Le Bristol Motor Speedway est une courte piste NASCAR située à Bristol, dans le Tennessee. La piste a la forme approximative illustrée sur la figure\(\PageIndex{11}\). Chaque extrémité de la piste est approximativement semi-circulaire, de sorte que lorsque les voitures font des virages, elles suivent une courbe approximativement circulaire. Si une voiture emprunte la voie intérieure et avance à toute vitesse au bas du virage 1, elle parcourt un demi-cercle d'un rayon d'environ 211 pieds avec un angle d'inclinaison de 24°. Si la voiture décide de prendre la voie extérieure et prend de la vitesse en haut du virage 1, elle parcourt un demi-cercle avec un angle d'inclinaison de 28°. (L'inclinaison de la piste est variable.)

Le coefficient de frottement d'un pneu normal sur sol sec est d'environ 0,7. Par conséquent, nous supposons que le coefficient d'un pneu NASCAR sur sol sec est d'environ 0,98.
Avant de répondre aux questions suivantes, notez qu'il est plus facile de faire des calculs en termes de pieds et de secondes, puis de convertir les réponses en miles par heure comme étape finale.
- Par temps sec, à quelle vitesse la voiture peut-elle parcourir le bas du virage sans déraper ?
- Par temps sec, à quelle vitesse la voiture peut-elle franchir le sommet du virage sans déraper ?
- Dans des conditions humides, le coefficient de frottement peut descendre jusqu'à 0,1. Si tel est le cas, à quelle vitesse la voiture peut-elle parcourir le bas du virage sans déraper ?
- Supposons que la vitesse mesurée d'une voiture qui longe le bord extérieur du virage soit de 105 mi/h. Estimez le coefficient de friction des pneus de la voiture.
Concepts clés
- Si\(\vecs{r}(t)\) représente la position d'un objet à l'instant t, puis\(\vecs{r}'(t)\) représente la vitesse et\(\vecs{r}′′(t)\) représente l'accélération de l'objet à l'instant t. L'amplitude du vecteur de vitesse est la vitesse.
- Le vecteur d'accélération pointe toujours vers le côté concave de la courbe définie par\(\vecs{r}(t)\). Les composantes tangentielles et normales de l'accélération\(a_\vecs{T}\)\(a_\vecs{N}\) sont les projections du vecteur d'accélération sur la tangente unitaire et les vecteurs normaux unitaires à la courbe.
- Les trois lois du mouvement planétaire de Kepler décrivent le mouvement des objets en orbite autour du Soleil. Sa troisième loi peut également être modifiée pour décrire le mouvement des objets en orbite autour d'autres objets célestes.
- Newton a pu utiliser sa loi de gravitation universelle en conjonction avec sa deuxième loi du mouvement et du calcul pour prouver les trois lois de Kepler.
Équations clés
- Vitesse\[\vecs{v}(t)=\vecs{r}′(t) \nonumber \]
- accélération\[\vecs{a}(t)=\vecs{v}′(t)=\vecs{r}′′(t) \nonumber \]
- Vitesse\[v(t)=||\vecs{v}(t)||=||\vecs{r}′(t)||=\dfrac{ds}{dt} \nonumber \]
- Composante tangentielle de l'accélération\[a_{\vecs{T}} =\vecs{a}\cdot \vecs{T}=\dfrac{\vecs{v}\cdot \vecs{a}}{||\vecs v||} \nonumber \]
- Composante normale de l'accélération\[a_{\vecs{N}}=\vecs{a}\cdot \vecs{N} = \dfrac{|| \vecs{v} \times \vecs{a} ||}{||\vecs{v}||} = \sqrt{||\vecs{a}||^2 - a_{\vecs{T}}} \nonumber \]
Lexique
- vecteur d'accélération
- la dérivée seconde du vecteur de position
- Les lois de Kepler sur le mouvement planétaire
- trois lois régissant le mouvement des planètes, des astéroïdes et des comètes en orbite autour du Soleil
- composante normale de l'accélération
- le coefficient du vecteur normal unitaire\(\vecs N\) lorsque le vecteur d'accélération est écrit sous la forme d'une combinaison linéaire de\(\vecs T\) et\(\vecs N\)
- mouvement du projectile
- mouvement d'un objet avec une vitesse initiale mais aucune force agissant sur celui-ci autre que la gravité
- composante tangentielle de l'accélération
- le coefficient du vecteur tangent unitaire\(\vecs T\) lorsque le vecteur d'accélération est écrit sous la forme d'une combinaison linéaire de\(\vecs T\) et\(\vecs N\)
- vecteur de vitesse
- la dérivée du vecteur de position
Contributeurs et attributions
- Template:ContribOpenStaxCalc
- Edited by Paul Seeburger
Paul Seeburger added finding point \((1, 2)\) when \(t=1\) in Example \(\PageIndex{1}\).
He also created Figure \(\PageIndex{1}\).


