Skip to main content
Global

12.8 : Exercices de révision du chapitre 12

  1. Last updated
  2. Save as PDF
  • Page ID
    197137

    • Edwin “Jed” Herman & Gilbert Strang
    • OpenStax
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Pour les exercices 1 à 4, déterminez si l'énoncé est vrai ou faux. Justifiez la réponse par une preuve ou un contre-exemple.

    1) Pour les vecteurs\(\vecs a\)\(\vecs b\) et tout scalaire donné\( c, \, c(\vecs a⋅\vecs b)=(c\vecs a)⋅\vecs b.\)

    Réponse
    Vrai ; voir preuve dans la section 11.3

    2) Pour les vecteurs\(\vecs a\)\(\vecs b\) et tout scalaire donné\( c, \, c(\vecs a×\vecs b)=(c\vecs a)×\vecs b\).

    3) L'équation symétrique de la ligne d'intersection entre deux plans\( x+y+z=2\) et\( x+2y−4z=5\) est donnée par\( −\frac{x−1}{6}=\frac{y−1}{5}=z.\)

    Réponse
    Faux, en convertissant les équations symétriques ci-dessus en équations paramétriques de la droite, nous obtenons :
    \(x = 1 - 6t\)
    \(y = 1 + 5t\)
    \(z = t\)

    Si cette droite se trouve sur chaque plan, nous devrions obtenir une identité (comme 5 = 5) lorsque nous substituez chaque expression de\(t\) dans l'équation de chaque plan.

    En la substituant dans l'équation du premier plan, nous obtenons :\( (1-6t) + (1+5t) + t = 2\,\checkmark\)

    Ainsi, nous savons que cette droite se trouve sur le premier plan.

    Mais lorsque nous la substituons à l'équation du deuxième plan, nous obtenons :\( (1 - 6t) + 2(1 + 5t) - 4(t) = 1 - 6t + 2 + 10t - 4t = 3 \neq 5\)

    Puisque nous n'obtenons pas d'identité, nous savons que cette droite ne se trouve pas sur le deuxième plan et ne peut donc pas être la ligne d'intersection du deux avions.

    4) Si\(\vecs a⋅\vecs b=0,\) alors\(\vecs a\) est perpendiculaire à\(\vecs b\).

    Réponse
    Faux, puisque\(\vecs a\) ou\(\vecs b\) pourrait également être le vecteur zéro.

    Pour les exercices 5 et 6, utilisez les vecteurs donnés pour trouver les quantités.

    5)\(\vecs a=9\hat{\mathbf{i}}−2\hat{\mathbf{j}},\quad \vecs b=−3\hat{\mathbf{i}}+\hat{\mathbf{k}}\)

    un.\( 3\vecs a+\vecs b\)

    b.\( \|\vecs a\|\)

    c.\(\vecs a×\|\vecs b×\vecs a\|\)

    d.\( \|\vecs b×\vecs a\|\)

    Réponse
    a.\( ⟨24,−6, 1⟩\)
    b.\( \sqrt{85}\)
    c. Impossible de croiser un vecteur avec un scalaire
    d.\( 11\)

    6)\(\vecs a=2\hat{\mathbf{i}}+\hat{\mathbf{j}}−9\hat{\mathbf{k}},\quad \vecs b=−\hat{\mathbf{i}}+2\hat{\mathbf{k}},\quad \vecs c=4\hat{\mathbf{i}}−2\hat{\mathbf{j}}+\hat{\mathbf{k}}\)

    un.\( 2\vecs a−\vecs b\)

    b.\( \|\vecs b×\vecs c\|\)

    c.\( \vecs b×\left(\vecs b×\vecs c\right)\)

    d.\( \vecs c×\|\vecs b×\vecs a\|\)

    e.\( \text{Proj}_\vecs{a}\vecs b\)

    7) Trouvez les valeurs de\(a\) tels vecteurs\( ⟨2,4,a⟩\) et qui\( ⟨0,−1,a⟩\) sont orthogonales.

    Réponse
    \( a=±2\)

    Pour les exercices 8 et 9, trouvez les vecteurs unitaires.

    8) Trouvez le vecteur unitaire qui a la même direction que le vecteur\(\vecs v\) qui commence\( (0,−3)\) et se termine à\( (4,10).\)

    9) Trouvez le vecteur unitaire qui a la même direction que le vecteur\(\vecs v\) qui commence\( (1,4,10)\) et se termine à\( (3,0,4).\)

    Réponse
    \( ⟨\frac{1}{\sqrt{14}},−\frac{2}{\sqrt{14}},−\frac{3}{\sqrt{14}}⟩ = ⟨\frac{\sqrt{14}}{14},−\frac{\sqrt{14}}{7},−\frac{3\sqrt{14}}{14}⟩ \)

    Pour les exercices 10 et 11, trouvez la surface ou le volume des formes données.

    10) Le parallélogramme parcouru par des vecteurs\(\vecs a=⟨1,13⟩\) et\(\vecs b=⟨3,21⟩\)

    11) Le parallélépipède formé par\(\vecs a=⟨1,4,1⟩\)\(\vecs b=⟨3,6,2⟩,\) et\(\vecs c=⟨−2,1,−5⟩\)

    Réponse
    \( 27\)unités\(^2\)

    Pour les exercices 12 et 13, trouvez les équations paramétriques et l'équation vectorielle de la droite avec les propriétés données.

    12) La ligne qui passe par un point\( (2,−3,7)\) parallèle au vecteur\( ⟨1,3,−2⟩\)

    13) La ligne qui passe par des points\( (1,3,5)\) et\( (−2,6,−3)\)

    Réponse
    \( x=1−3t,y=3+3t,z=5−8t,\quad \vecs r(t)=(1−3t)\hat{\mathbf{i}}+3(1+t)\hat{\mathbf{j}}+(5−8t)\hat{\mathbf{k}}\)

    Pour les exercices 14 et 15, trouvez l'équation du plan avec les propriétés données.

    14) Le plan qui passe par le point\( (4,7,−1)\) et qui a un vecteur normal\(\vecs n=⟨3,4,2⟩\)

    15) Le plan qui passe par des points\( (0,1,5),(2,−1,6),\) et\( (3,2,5).\)

    Réponse
    \( −x+3y+8z=43\)

    Pour les exercices 16 et 17, trouvez les traces des surfaces dans les plans\( x=k,y=k\),\( z=k.\) puis décrivez et dessinez les surfaces.

    16)\( 9x^2+4y^2−16y+36z^2=20\)

    17)\( x^2=y^2+z^2\)

    Réponse
    \( x=k\)trace :\( k^2=y^2+z^2\) est un cercle,\( y=k\) trace :\( x^2−z^2=k^2\) est une hyperbole (ou une paire de lignes si\( k=0), z=k\) trace :\( x^2−y^2=k^2\) est une hyperbole (ou une paire de lignes si\( k=0\)). La surface est un cône.

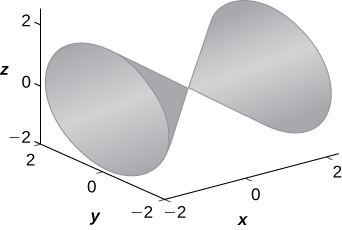
    Pour les exercices 18 et 19, écrivez l'équation donnée en coordonnées cylindriques et en coordonnées sphériques.

    18)\( x^2+y^2+z^2=144\)

    19)\( z=x^2+y^2−1\)

    Réponse
    Cylindrique :\( z=r^2−1,\) sphérique :\( \cos φ=ρ\sin^2 φ−\frac{1}{ρ}\)

    Pour les exercices 20 et 21, convertissez les équations données des coordonnées cylindriques ou sphériques en coordonnées rectangulaires. Identifiez la surface donnée.

    (20)\( ρ^2(\sin^2(φ)−\cos^2(φ))=1\)

    (21)\( r^2−2r\cos(θ)+z^2=1\)

    Réponse
    \( x^2−2x+y^2+z^2=1\), sphère

    Pour les exercices 22 et 23, imaginez un petit bateau qui traverse une rivière.

    22) Si la vitesse du bateau est de\( 5\) km/h plein nord en eau calme et que l'eau a un courant de\( 2\) km/h plein ouest (voir la figure suivante), quelle est la vitesse du bateau par rapport à la rive ? Quel est l'angle\( θ\) de déplacement réel du bateau ?

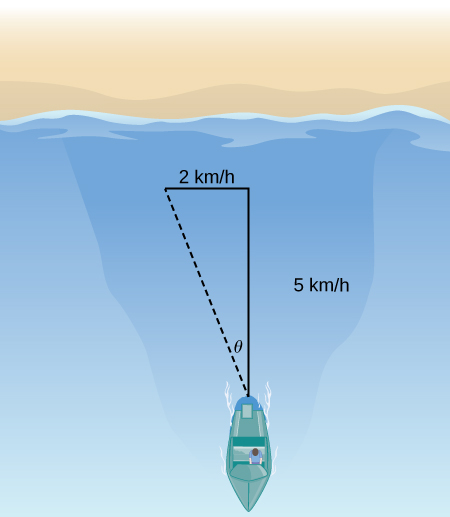
    23) Lorsque le bateau atteint le rivage, deux cordes sont lancées sur les personnes pour aider à tirer le bateau à terre. Une corde est inclinée\( 25°\) et l'autre est inclinée\( 35°\). Si le bateau doit être tiré en ligne droite avec une force de\( 500\) N, déterminez l'amplitude de la force pour chaque corde (voir la figure suivante).

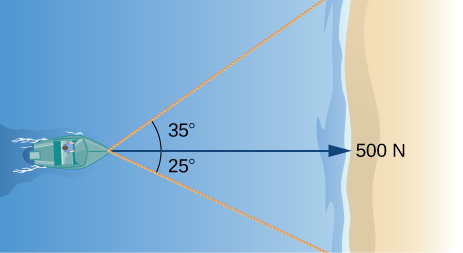
    Réponse
    331 N et 244 N

    24) Un avion vole dans la direction de 52° à l'est du nord à une vitesse de 450 mi/h. Un vent fort s'élève à 33° à l'est du nord à une vitesse de 50 mi/h. Quelles sont la vitesse au sol et l'orientation résultantes de l'avion ?

    25) Calculez le travail effectué en déplaçant une particule d'une position\( (1,2,0)\) à l'autre\( (8,4,5)\) le long d'une ligne droite avec une force\(\vecs F=2\hat{\mathbf{i}}+3\hat{\mathbf{j}}−\hat{\mathbf{k}}.\)

    Réponse
    \( 15\)J

    Dans les problèmes 26 et 27, considérez votre tentative infructueuse de démonter le pneu de votre voiture à l'aide d'une clé pour desserrer les boulons. Supposons que la clé mesure\( 0.3\) 5 m de long et que vous pouvez appliquer une force de 200 N.

    26) Comme votre pneu est crevé, vous ne pouvez appliquer votre force que de manière\( 60°\) inclinée. Quel est le couple au centre du boulon ? Supposons que cette force ne soit pas suffisante pour desserrer le verrou.

    27) Quelqu'un vous prête un cric à pneu et vous pouvez maintenant appliquer une force de 200 N à un\( 80°\) angle. Le couple qui en résultera sera-t-il plus ou moins élevé ? Quel est le nouveau couple obtenu au centre du boulon ? Supposons que cette force ne soit pas suffisante pour desserrer le verrou.

    Réponse
    Plus,\( 59.09\) J