12.6 : Surfaces quadriques

Last updated
Save as PDF

Page ID: 197143

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objectifs d'apprentissage

Identifiez un cylindre en tant que type de surface tridimensionnelle.
Reconnaissez les principales caractéristiques des ellipsoïdes, des paraboloïdes et des hyperboloïdes.
Utilisez des tracés pour dessiner les intersections des surfaces quadriques avec les plans de coordonnées.

Nous avons exploré des vecteurs et des opérations vectorielles dans l'espace tridimensionnel, et nous avons développé des équations pour décrire des lignes, des plans et des sphères. Dans cette section, nous utilisons notre connaissance des plans et des sphères, qui sont des exemples de figures tridimensionnelles appelées surfaces, pour explorer diverses autres surfaces qui peuvent être représentées graphiquement dans un système de coordonnées tridimensionnel.

Identification des cylindres

La première surface que nous allons examiner est le cylindre. Bien que la plupart des gens pensent immédiatement à un tuyau creux ou à une paille de soda lorsqu'ils entendent le mot cylindre, nous utilisons ici le sens mathématique large du terme. Comme nous l'avons vu, les surfaces cylindriques n'ont pas besoin d'être circulaires. Un conduit de chauffage rectangulaire est un cylindre, tout comme un tapis de yoga enroulé dont la section transversale est en forme de spirale.

Dans le plan de coordonnées bidimensionnel, l'équation$ x^2+y^2=9$ décrit un cercle centré à l'origine avec un rayon$ 3$. Dans l'espace tridimensionnel, cette même équation représente une surface. Imaginez des copies d'un cercle empilé l'un sur l'autre centré sur l'$z$axe (Figure$\PageIndex{1}$), formant un tube creux. Nous pouvons ensuite construire un cylindre à partir de l'ensemble de lignes parallèles à l'$z$axe -passant par le cercle$ x^2+y^2=9$ dans le$xy$ plan, comme indiqué sur la figure. Ainsi, n'importe quelle courbe dans l'un des plans de coordonnées peut être étendue pour devenir une surface.

Cette figure est un système de coordonnées en 3 dimensions. Il a un centre circulaire droit avec l'axe Z passant par le centre. Le cylindre possède également des points marqués sur les axes x et y à (3, 0, 0) et (0, 3, 0). — Figure$\PageIndex{1}$ : Dans un espace tridimensionnel, le graphe de l'équation$ x^2+y^2=9$ est un cylindre dont le rayon est$ 3$ centré sur l'$z$axe. Elle se poursuit indéfiniment dans les directions positive et négative.

Définition : cylindres et gouvernes

Un ensemble de lignes parallèles à une ligne donnée passant par une courbe donnée est connu sous le nom de surface cylindrique, ou cylindre. Les lignes parallèles sont appelées règles.

À partir de cette définition, nous pouvons voir que nous avons toujours un cylindre dans l'espace tridimensionnel, même si la courbe n'est pas un cercle. Toute courbe peut former un cylindre, et les règles qui le composent peuvent être parallèles à n'importe quelle ligne (Figure$\PageIndex{2}$).

Cette figure possède une surface tridimensionnelle qui commence sur l'axe Y et se courbe vers le haut. Les axes x et z sont également étiquetés. — Figure$\PageIndex{2}$ : Dans un espace tridimensionnel, le graphique de l'équation$ z=x^3$ est un cylindre ou une surface cylindrique dont les règles sont parallèles à l'$y$axe.

Exemple$ \PageIndex{1}$: Graphing Cylindrical Surfaces

Esquissez les graphes des surfaces cylindriques suivantes.

$ x^2+z^2=25$
$ z=2x^2−y$
$ y=\sin x$

Solution

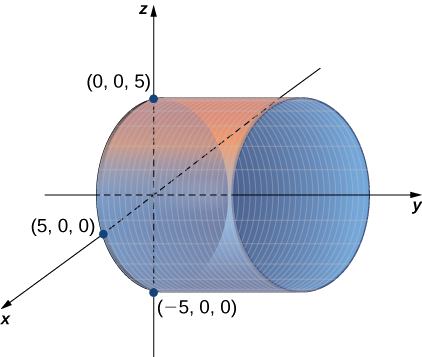
a. La variable$ y$ peut prendre n'importe quelle valeur sans limite. Par conséquent, les lignes qui régissent cette surface sont parallèles à l'$y$axe. L'intersection de cette surface avec le$xz$ plan forme un cercle centré à l'origine avec un rayon$ 5$ (voir Figure$\PageIndex{3}$).

Cette figure représente le système de coordonnées en 3 dimensions. Il possède un cylindre circulaire droit sur le côté avec l'axe Y au centre. Le cylindre coupe l'axe X en (5, 0, 0). Il possède également deux points d'intersection étiquetés sur l'axe z à (0, 0, 5) et (0, 0, -5). — Figure$\PageIndex{3}$ : Le graphique de l'équation$ x^2+z^2=25$ est un cylindre dont le rayon est$ 5$ centré sur l'$y$axe.

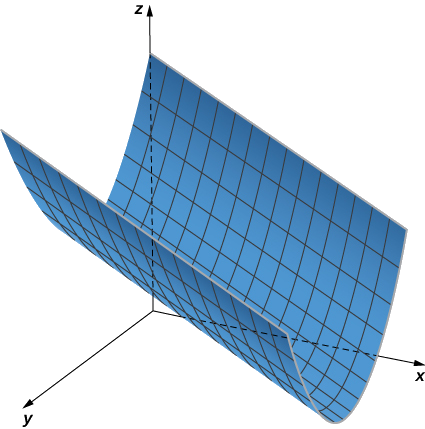
b. Dans ce cas, l'équation contient les trois variables —$ x,y,$ et$ z$ — donc aucune des variables ne peut varier arbitrairement. Le moyen le plus simple de visualiser cette surface est d'utiliser un utilitaire de création graphique par ordinateur (Figure$\PageIndex{4}$).

Cette figure présente une surface dans le premier octant. La section transversale du solide est une parabole. — Figurine$\PageIndex{4}$

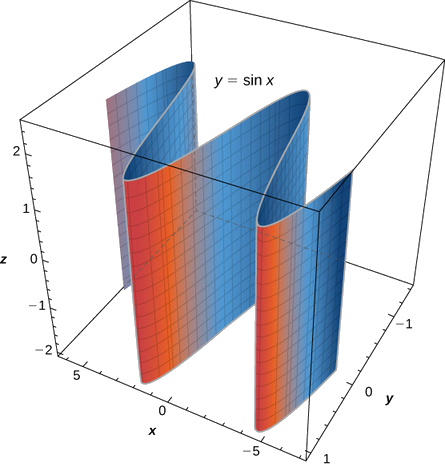
c. Dans cette équation, la variable$ z$ peut prendre n'importe quelle valeur sans limite. Par conséquent, les lignes composant cette surface sont parallèles à l'$z$axe. L'intersection de cette surface avec le plan xy délimite la courbe$ y=\sin x$ (Figure$\PageIndex{5}$).

Cette figure est une surface tridimensionnelle. Une coupe transversale de la surface parallèle au plan x y serait la courbe sinusoïdale. — Figure$\PageIndex{5}$ : Le graphique de l'équation$ y=\sin x$ est formé par un ensemble de droites parallèles à l'$z$axe -passant par une courbe$ y=\sin x$ dans le$xy$ plan.

Exercice$ \PageIndex{1}$:

Esquissez ou utilisez un outil graphique pour visualiser le graphique de la surface cylindrique définie par l'équation$ z=y^2$.

Allusion: La variable$ x$ peut prendre n'importe quelle valeur sans limite.
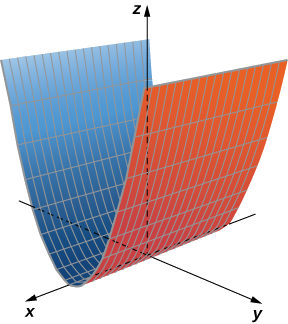
Réponse: $Cette figure est une surface au-dessus du plan x y. Une coupe transversale de cette surface parallèle au plan y z serait une parabole. La surface se trouve au-dessus du plan x y.$

Lors de l'esquisse de surfaces, nous avons vu qu'il est utile d'esquisser l'intersection de la surface avec un plan parallèle à l'un des plans de coordonnées. Ces courbes sont appelées traces. Nous pouvons les voir sur le tracé du cylindre de la figure$\PageIndex{6}$.

Définition : traces

Les traces d'une surface sont les coupes transversales créées lorsque la surface croise un plan parallèle à l'un des plans de coordonnées.

Les traces sont utiles pour dessiner des surfaces cylindriques. Cependant, pour un cylindre en trois dimensions, un seul ensemble de traces est utile. Remarquez, sur la figure$\PageIndex{6}$, que la trace du graphe de$ z=\sin x$ dans le plan xz est utile pour construire le graphe. La trace dans le plan xy, cependant, n'est qu'une série de lignes parallèles, et la trace dans le plan yz est simplement une ligne.

Cette figure comporte deux images. La première image est une surface. Une coupe transversale de la surface parallèle au plan x z serait une courbe sinusoïdale. La deuxième image est la courbe sinusoïdale dans le plan x y. — Figure$\PageIndex{6}$ : (a) Il s'agit d'une vue du graphique de l'équation$ z=\sin x$. (b) Pour trouver la trace du graphe dans le$xz$ plan, définissez$ y=0$. La trace est simplement une onde sinusoïdale bidimensionnelle.

Les surfaces cylindriques sont formées par un ensemble de lignes parallèles. Cependant, toutes les surfaces en trois dimensions ne sont pas construites aussi simplement. Nous explorons maintenant des surfaces plus complexes, et les traces constituent un outil important dans cette étude.

Surfaces quadriques

Nous avons découvert des surfaces en trois dimensions décrites par des équations du premier ordre ; ce sont des plans. D'autres types courants de surfaces peuvent être décrits par des équations du second ordre. Nous pouvons voir ces surfaces comme des extensions tridimensionnelles des sections coniques dont nous avons parlé précédemment : l'ellipse, la parabole et l'hyperbole. Nous appelons ces graphes des surfaces quadriques

Définition : Surfaces quadriques et sections coniques

Les surfaces quadriques sont les graphes d'équations qui peuvent être exprimées sous la forme

\[Ax^2+By^2+Cz^2+Dxy+Exz+Fyz+Gx+Hy+Jz+K=0. \nonumber \]

Lorsqu'une surface quadrique croise un plan de coordonnées, la trace est une section conique.

Un ellipsoïde est une surface décrite par une équation de la forme$ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}=1.$ Set$ x=0$ pour voir la trace de l'ellipsoïde dans le plan yz. Pour voir les traces dans les$xz$ plans$xy$ - et -, respectivement$ y=0$, définissez$ z=0$ et. Notez que, si$ a=b$, la trace dans le$xy$ plan est un cercle. De même$ a=c$, si, la trace dans le$xz$ plan est un cercle et, si$ b=c$, alors la trace dans le$yz$ plan est un cercle. Une sphère est donc un ellipsoïde avec$ a=b=c.$

Exemple$ \PageIndex{2}$: Sketching an Ellipsoid

Esquissez l'ellipsoïde

\[ \dfrac{x^2}{2^2}+\dfrac{y^2}{3^2}+\dfrac{z^2}{5^2}=1. \nonumber \]

Solution

Commencez par dessiner les traces. Pour trouver la trace dans le plan xy, définissez$ z=0: \dfrac{x^2}{2^2}+\dfrac{y^2}{3^2}=1$ (Figure$\PageIndex{7}$). Pour trouver les autres traces, commencez par définir,$ y=0$ puis définissez$ x=0.$

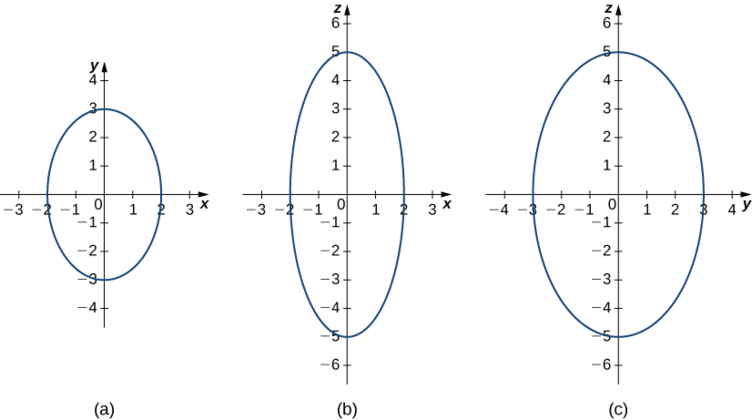
Cette figure comporte trois images. La première image est un ovale centré autour de l'origine du système de coordonnées rectangulaires. Il coupe l'axe x en -2 et en 2. Il coupe l'axe Y en -3 et en 3. La deuxième image est un ovale centré autour de l'origine du système de coordonnées rectangulaires. Il coupe l'axe X en -2 et 2 et l'axe y en -5 et 5. La troisième image est un ovale centré autour de l'origine du système de coordonnées rectangulaires. Il coupe l'axe X en -3 et 3 et l'axe y en -5 et 5. — Figure$\PageIndex{7}$ : (a) Ce graphique représente la trace de l'équation$ \dfrac{x^2}{2^2}+\dfrac{y^2}{3^2}+\dfrac{z^2}{5^2}=1$ dans le$xy$ plan -, lorsque nous sommes définis$ z=0$. (b) Lorsque nous nous fixons$ y=0$, nous obtenons la trace de l'ellipsoïde dans le$xz$ plan -, qui est une ellipse. (c) Lorsque nous nous fixons$ x=0$, nous obtenons la trace de l'ellipsoïde dans le$yz$ plan -, qui est également une ellipse.

Maintenant que nous savons à quoi ressemblent les traces de ce solide, nous pouvons esquisser la surface en trois dimensions (Figure$\PageIndex{8}$).

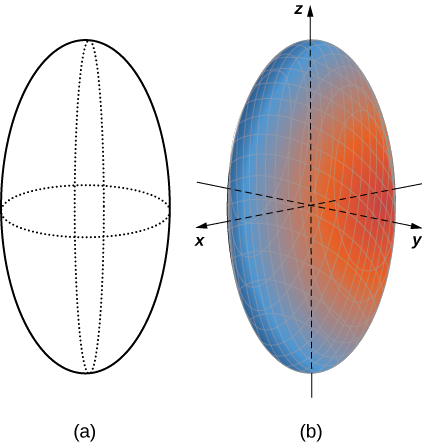
Cette figure comporte deux images. La première image est une ellipse verticale. Deux courbes sont tracées avec des lignes pointillées autour du centre horizontalement et verticalement pour donner à l'image une forme tridimensionnelle. La deuxième image est une forme elliptique solide dont le centre est à l'origine du système de coordonnées tridimensionnel. — Figure$\PageIndex{8}$ : (a) Les traces fournissent un cadre pour la surface. (b) Le centre de cet ellipsoïde est l'origine.

La trace d'un ellipsoïde est une ellipse dans chacun des plans de coordonnées. Toutefois, cela ne doit pas nécessairement être le cas pour toutes les surfaces quadriques. De nombreuses surfaces quadriques présentent des traces qui correspondent à différents types de sections coniques, ce qui est généralement indiqué par le nom de la surface. Par exemple, si une surface peut être décrite par une équation de la forme

\[ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=\dfrac{z}{c} \nonumber \]

alors on appelle cette surface un paraboloïde elliptique. La trace dans le plan xy est une ellipse, mais les traces dans le plan xz et le plan yz sont des paraboles (Figure$\PageIndex{9}$). D'autres paraboloïdes elliptiques peuvent avoir d'autres orientations simplement en interchangeant les variables pour nous donner une variable différente dans le terme linéaire de l'équation$ \dfrac{x^2}{a^2}+\dfrac{z^2}{c^2}=\dfrac{y}{b}$ ou$ \dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}=\dfrac{x}{a}$.

Cette figure est l'image d'une surface. Il se trouve dans le système de coordonnées tridimensionnel au-dessus de l'origine. Une coupe transversale de cette surface parallèle au plan x y serait une ellipse. — Figure$\PageIndex{9}$ : Cette surface quadrique est appelée paraboloïde elliptique.

Exemple$ \PageIndex{3}$: Identifying Traces of Quadric Surfaces

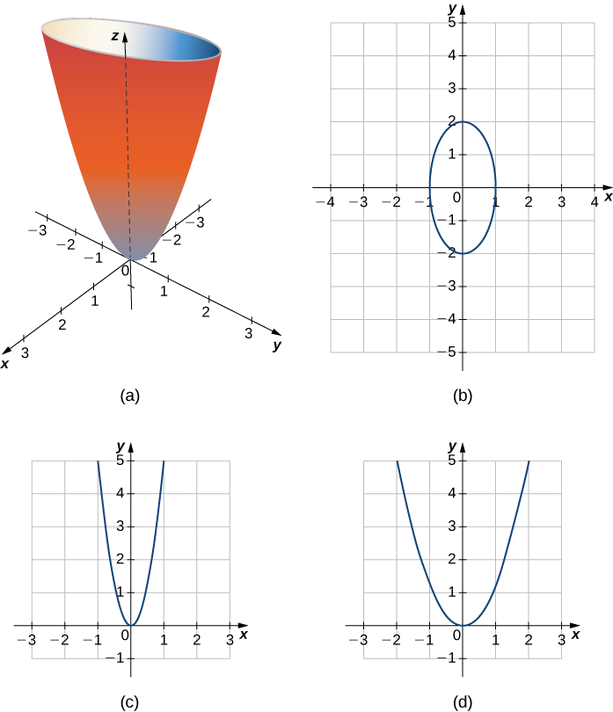
Décrivez les traces du paraboloïde elliptique$ x^2+\dfrac{y^2}{2^2}=\dfrac{z}{5}$.

Solution

Pour trouver la trace dans le$xy$ plan, définissez$ z=0: x^2+\dfrac{y^2}{2^2}=0.$ La trace dans le plan$ z=0$ est simplement un point, l'origine. Comme un seul point ne nous indique pas quelle est la forme, nous pouvons remonter l'$z$axe -vers un plan arbitraire pour trouver la forme d'autres traces de la figure.

La trace dans le plan$ z=5$ est le graphe de l'équation$ x^2+\dfrac{y^2}{2^2}=1$, qui est une ellipse. Dans le$xz$ plan -, l'équation devient$ z=5x^2$. La trace est une parabole dans ce plan et dans n'importe quel plan avec l'équation$ y=b$.

Dans les plans parallèles au$yz$ plan -, les traces sont également des paraboles, comme on peut le voir sur la Figure$\PageIndex{10}$.

Cette figure comporte quatre images. La première image est l'image d'une surface. Il se trouve dans le système de coordonnées tridimensionnel au-dessus de l'origine. Une coupe transversale de cette surface parallèle au plan x y serait une ellipse. Une section transversale parallèle au plan x z serait une parabole. Une coupe transversale de la surface parallèle au plan y z serait une parabole. La deuxième image est la coupe transversale parallèle au plan x y et est une ellipse. La troisième image est la coupe transversale parallèle au plan x z et est une parabole. La quatrième image est la coupe transversale parallèle au plan y z et est une parabole. — Figure$\PageIndex{10}$ : (a) Le paraboloïde$ x^2+\dfrac{y^2}{2^2}=\dfrac{z}{5}$. (b) La trace dans l'avion$ z=5$. (c) La trace dans le$xz$ plan. (d) La trace dans le$yz$ plan.

Exercice$ \PageIndex{2}$:

Un hyperboloïde d'une feuille est toute surface qui peut être décrite à l'aide d'une équation de la forme$ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=1$. Décrire les traces de l'hyperboloïde d'une feuille donnée par équation$ \dfrac{x^2}{3^2}+\dfrac{y^2}{2^2}−\dfrac{z^2}{5^2}=1.$

Allusion

Pour trouver les traces dans les plans de coordonnées, définissez chaque variable sur zéro individuellement.

Réponse

Les traces parallèles au$xy$ plan -sont des ellipses et les traces parallèles aux$yz$ plans$xz$ - et -sont des hyperboles. Plus précisément, la trace dans le$xy$ plan est une ellipse,$ \dfrac{x^2}{3^2}+\dfrac{y^2}{2^2}=1,$ la trace dans le$xz$ plan -est une hyperbole$ \dfrac{x^2}{3^2}−\dfrac{z^2}{5^2}=1,$ et la trace dans le$yz$ plan -est une hyperbole$ \dfrac{y^2}{2^2}−\dfrac{z^2}{5^2}=1$ (voir la figure suivante).

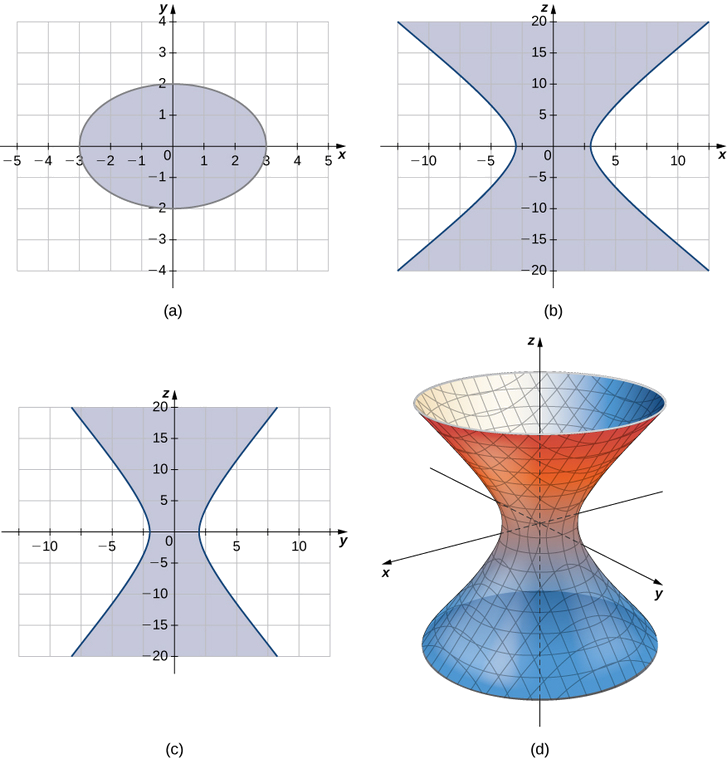
$Cette figure comporte quatre images. La première image est une ellipse centrée à l'origine d'un système de coordonnées rectangulaires. Il coupe l'axe x en -3 et 3. Il coupe l'axe y en -2 et en 2. La deuxième image est le graphique d'une hyperbole. Il s'agit de deux courbes, l'une s'ouvrant dans la direction x négative et l'autre symétrique dans la direction x positive. La troisième image est le graphique d'une hyperbole dans le plan y z. Elle s'ouvre dans la direction y négative et une courbe symétrique s'ouvre dans la direction y positive. La quatrième image est une surface tridimensionnelle. Ses sections transversales supérieure et inférieure seraient circulaires. Une intersection verticale serait une hyperbole.$

Les hyperboloïdes d'une feuille ont des propriétés fascinantes. Par exemple, ils peuvent être construits en utilisant des lignes droites, comme dans la sculpture de la figure$\PageIndex{11a}$. En fait, les tours de refroidissement des centrales nucléaires sont souvent construites sous la forme d'un hyperboloïde. Les constructeurs peuvent utiliser des poutres d'acier droites pour la construction, ce qui rend les tours très solides tout en utilisant relativement peu de matériaux (Figure$\PageIndex{11b}$).

Cette figure comporte deux images. La première image est une sculpture faite de bâtons parallèles, incurvés ensemble en un cercle avec une section transversale hyperbolique. La deuxième image montre une centrale nucléaire. Les tours sont de forme hyperbolique. — Figure$\PageIndex{11}$ : (a) Une sculpture en forme d'hyperboloïde peut être construite en lignes droites. (b) Les tours de refroidissement des centrales nucléaires sont souvent construites sous la forme d'un hyperboloïde.

Exemple$ \PageIndex{4}$: Chapter Opener: Finding the Focus of a Parabolic Reflector

L'énergie qui atteint la surface d'un réflecteur parabolique est concentrée au point focal du réflecteur (Figure$\PageIndex{12}$). Si la surface d'un réflecteur parabolique est décrite par une équation,$ \dfrac{x^2}{100}+\dfrac{y^2}{100}=\dfrac{z}{4},$ où se trouve le point focal du réflecteur ?

Cette figure comporte deux images. La première image est une image d'antennes paraboliques équipées de réflecteurs paraboliques. La deuxième image est une courbe parabolique sur un segment de droite. Le bas de la courbe se trouve au point V. Il y a un segment de droite perpendiculaire à l'autre segment de droite passant par V. Il y a un point sur ce segment de droite étiqueté F. Il y a 3 lignes allant de F à la parabole, se croisant en P sub 1, P sub 2 et P sub 3. Il existe également trois lignes verticales allant de P sub 1 à Q sub 1, de P sub 2 à Q sub 2 et de P sub 3 à Q sub 3. — Figure$\PageIndex{12}$ : L'énergie est réfléchie par le réflecteur parabolique et est collectée au point focal. (source : modification de CGP Grey, Wikimedia Commons)

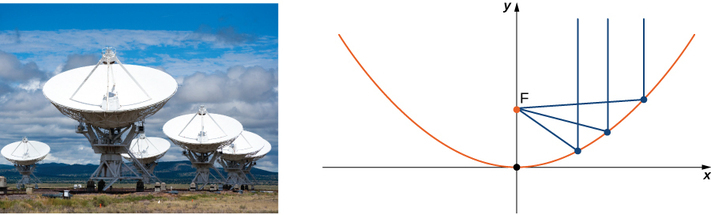
Solution

Comme z est la première variable de puissance, l'axe du réflecteur correspond à l'$z$axe. Les coefficients de l'$ x^2$ and $ y^2$ are equal, so the cross-section of the paraboloid perpendicular to the $z$axe -sont un cercle. Nous pouvons considérer une trace dans le plan xz ou dans le plan yz ; le résultat est le même. $ y=0$, the trace is a parabola opening up along the $z$Réglage de l'axe, avec équation standard$ x^2=4pz$, where $ p$ is the focal length of the parabola. In this case, this equation becomes $ x^2=100⋅\dfrac{z}{4}=4pz$ or $ 25=4p$. So p is $ 6.25$ m, which tells us that the focus of the paraboloid is $ 6.25$ m up the axis from the vertex. Because the vertex of this surface is the origin, the focal point is $ (0,0,6.25).$

Dix-sept surfaces quadriques standard peuvent être dérivées à partir de l'équation générale.

\[Ax^2+By^2+Cz^2+Dxy+Exz+Fyz+Gx+Hy+Jz+K=0. \nonumber \]

Les chiffres suivants résument les plus importants.

Cette figure représente un tableau à deux colonnes et trois rangées. Les trois rangées représentent les 6 premières surfaces quadriques : ellipsoïde, hyperboloïde d'une feuille et hyperboloïde de deux feuilles. Les équations et les traces se trouvent dans la première colonne. La deuxième colonne contient les graphes des surfaces. Le graphe ellipsoïdal est une forme ronde oblongue verticale. L'hyperboloïde d'une feuille est circulaire en haut et en bas et étroit au milieu. L'hyperboloïde en deux feuilles possède deux dômes paraboliques opposés. — Figure$\PageIndex{13}$ : Caractéristiques des surfaces quadriques communes : ellipsoïde, hyperboloïde d'une feuille, hyperboloïde de deux feuilles.

Cette figure représente un tableau à deux colonnes et trois rangées. Les trois rangées représentent les 6 surfaces quadriques suivantes : cône elliptique, paraboloïde elliptique et paraboloïde hyperbolique. Les équations et les traces se trouvent dans la première colonne. La deuxième colonne contient les graphes des surfaces. Le cône elliptique possède deux cônes qui se touchent au niveau des points. Le paraboloïde elliptique ressemble à un cône mais est oblong. Le paraboloïde hyperbolique présente une courbure au milieu semblable à celle d'une selle. — Figure$\PageIndex{14}$ : Caractéristiques des surfaces quadriques communes : cône elliptique, paraboloïde elliptique, paraboloïde hyperbolique.

Exemple$ \PageIndex{5}$: Identifying Equations of Quadric Surfaces

Identifiez les surfaces représentées par les équations données.

$ 16x^2+9y^2+16z^2=144$
$ 9x^2−18x+4y^2+16y−36z+25=0$

Solution

a. Les$ z$ termes$ x,y,$ et sont tous au carré et sont tous positifs, il s'agit donc probablement d'un ellipsoïde. Cependant, mettons l'équation sous la forme standard d'un ellipsoïde, juste pour être sûr. Nous avons

\[ 16x^2+9y^2+16z^2=144. \nonumber \]

Diviser par 144 donne

\[ \dfrac{x^2}{9}+\dfrac{y^2}{16}+\dfrac{z^2}{9}=1. \nonumber \]

Il s'agit donc en fait d'un ellipsoïde, centré à l'origine.

b. Nous remarquons d'abord que le$ z$ terme n'est élevé qu'à la première puissance, il s'agit donc soit d'un paraboloïde elliptique, soit d'un paraboloïde hyperbolique. Nous remarquons également que$ x$ certains termes ne sont pas carrés, de sorte que cette surface quadrique n'est pas centrée à l'origine.$ y$ Nous devons compléter le carré pour mettre cette équation dans l'une des formes standard. Nous avons

\[ \begin{align*} 9x^2−18x+4y^2+16y−36z+25 =0 \\[4pt] 9x^2−18x+4y^2+16y+25 =36z \\[4pt] 9(x^2−2x)+4(y^2+4y)+25 =36z \\[4pt] 9(x^2−2x+1−1)+4(y^2+4y+4−4)+25 =36z \\[4pt] 9(x−1)^2−9+4(y+2)^2−16+25 =36z \\[4pt] 9(x−1)^2+4(y+2)^2 =36z \\[4pt] \dfrac{(x−1)^2}{4}+\dfrac{(y−2)^2}{9} =z. \end{align*}\]

Il s'agit d'un paraboloïde elliptique centré sur$ (1,2,0).$

Exercice$ \PageIndex{3}$

Identifier la surface représentée par l'équation$ 9x^2+y^2−z^2+2z−10=0.$

Allusion: Examinez les signes et les$ x,y$ pouvoirs des$ z$ termes et
Réponse: Hyperboloïde d'une feuille, centré sur$ (0,0,1)$.

Concepts clés

Un ensemble de lignes parallèles à une ligne donnée passant par une courbe donnée est appelé cylindre, ou surface cylindrique. Les lignes parallèles sont appelées règles.
L'intersection d'une surface tridimensionnelle et d'un plan est appelée trace. Pour rechercher la trace dans les plans $xy$$yz$-,$xz$ - ou -, définir$ z=0,x=0,$ ou$ y=0,$ respectivement.
Les surfaces quadriques sont des surfaces tridimensionnelles dont les traces sont composées de sections coniques. Chaque surface quadrique peut être exprimée par une équation de la forme

\[Ax^2+By^2+Cz^2+Dxy+Exz+Fyz+Gx+Hy+Jz+K=0. \nonumber \]

Pour esquisser le graphe d'une surface quadrique, commencez par dessiner les traces afin de comprendre la structure de la surface.
Les surfaces quadriques importantes sont résumées dans les figures$\PageIndex{13}$ et$\PageIndex{14}$.

Lexique

cylindre: un ensemble de droites parallèles à une ligne donnée passant par une courbe donnée

ellipsoïde: une surface tridimensionnelle décrite par une équation de la forme$ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}=1$ ; toutes les traces de cette surface sont des ellipses

cône elliptique: une surface tridimensionnelle décrite par une équation de la forme$ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=0$ ; les traces de cette surface incluent des ellipses et des lignes qui se croisent

paraboloïde elliptique: une surface tridimensionnelle décrite par une équation de la forme$ z=\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}$ ; les traces de cette surface incluent des ellipses et des paraboles

hyperboloïde d'une feuille: une surface tridimensionnelle décrite par une équation de la forme, les$ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=1;$ traces de cette surface incluent des ellipses et des hyperboles

hyperboloïde de deux feuilles: une surface tridimensionnelle décrite par une équation de la forme$ \dfrac{z^2}{c^2}−\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1$ ; les traces de cette surface incluent des ellipses et des hyperboles

surfaces quadriques: surfaces en trois dimensions ayant la propriété que les traces de la surface sont des sections coniques (ellipses, hyperboles et paraboles)

décisions: lignes parallèles qui constituent une surface cylindrique

tracer: l'intersection d'une surface tridimensionnelle avec un plan de coordonnées

Définition : cylindres et gouvernes

Exemple\( \PageIndex{1}\): Graphing Cylindrical Surfaces

Exercice\( \PageIndex{1}\):

Définition : traces

Définition : Surfaces quadriques et sections coniques

Exemple\( \PageIndex{2}\): Sketching an Ellipsoid

Exemple\( \PageIndex{3}\): Identifying Traces of Quadric Surfaces

Exercice\( \PageIndex{2}\):

Exemple\( \PageIndex{4}\): Chapter Opener: Finding the Focus of a Parabolic Reflector

Exemple\( \PageIndex{5}\): Identifying Equations of Quadric Surfaces

Exercice\( \PageIndex{3}\)