12.5 : Équations des lignes et des plans dans l'espace

Objectifs d'apprentissage

• Ecrivez les équations vectorielles, paramétriques et symétriques d'une droite passant par un point donné dans une direction donnée, et d'une droite passant par deux points donnés.
• Détermine la distance entre un point et une ligne donnée.
• Ecrivez les équations vectorielles et scalaires d'un plan passant par un point donné avec une normale donnée.
• Détermine la distance entre un point et un plan donné.
• Détermine l'angle entre deux plans.

À ce jour, nous sommes habitués à écrire des équations qui décrivent une ligne en deux dimensions. Pour écrire une équation pour une droite, nous devons connaître deux points sur la ligne, ou nous devons connaître la direction de la droite et au moins un point par lequel passe la droite. En deux dimensions, nous utilisons le concept de pente pour décrire l'orientation, ou la direction, d'une ligne. En trois dimensions, nous décrivons la direction d'une ligne à l'aide d'un vecteur parallèle à la droite. Dans cette section, nous examinons comment utiliser des équations pour décrire des lignes et des plans dans l'espace.

Équations pour une droite dans l'espace

Voyons d'abord ce que signifie le fait que deux vecteurs soient parallèles. Rappelons que les vecteurs parallèles doivent avoir des directions identiques ou opposées. Si deux vecteurs non nuls,\( \vecs{u}\) et\( \vecs{v}\), sont parallèles, nous prétendons qu'il doit y avoir un scalaire\( k\),, tel que\( \vecs{u}=k\vecs{v}\). Si\( \vecs{u}\) et\( \vecs{v}\) avez la même direction, il vous suffit de choisir

\[ k=\dfrac{‖\vecs{u}‖}{‖\vecs{v}‖}. \nonumber \]

Si\( \vecs{u}\) et\( \vecs{v}\) ont des directions opposées, choisissez

\[ k=−\dfrac{‖\vecs{u}‖}{‖\vecs{v}‖}. \nonumber \]

Notez que l'inverse est également valable. S'il s'agit\( \vecs{u}=k \vecs{v}\) d'un scalaire\( k\), alors soit\( \vecs{u}\)\(\vecs{ v}\) ont la même direction,\( (k>0)\) soit des directions opposées\( (k<0)\), donc\( \vecs{u}\) et\( \vecs{v}\) sont parallèles. Par conséquent, deux vecteurs non nuls\( \vecs{u}\) et\(\vecs{ v}\) sont parallèles si et seulement s'il s'\( \vecs{u}=k\vecs{v}\)agit d'un scalaire\( k\). Par convention, le vecteur zéro\( \vecs{0}\) est considéré comme étant parallèle à tous les vecteurs.

Figure\(\PageIndex{1}\) : Le vecteur\(\vecs{v}\) est le vecteur de direction de\( \vecd{PQ}\).

Comme en deux dimensions, nous pouvons décrire une ligne dans l'espace à l'aide d'un point sur la ligne et de la direction de la ligne, ou d'un vecteur parallèle, que nous appelons vecteur de direction (Figure\(\PageIndex{1}\)). \( L\)Soit une ligne dans l'espace passant par un point\( P(x_0,y_0,z_0)\). \( \vecs{v}=⟨a,b,c⟩\)Soit un vecteur parallèle à\( L\). Ensuite, pour tout point en ligne\( Q(x,y,z)\), nous savons que\( \vecd{PQ}\) c'est parallèle à\( \vecs{v}\). Ainsi, comme nous venons de le dire, il existe un scalaire\( t\), tel que\( \vecd{PQ}=t\vecs{v}\), qui donne

\ [\ begin {align} \ vecd {PQ} &=t \ vecs {v} \ nonumber \ \ [4pt]
⌘x−x_0, y−y_0, z−z_0⟩ &=ttra-a, b, c⟩ \ nonumber \ \ [4pt]
⌘x−x_0, y−y_0, z−z_0⟩ &=⌘ta, tb, tc⟩. \ label {eq1} \ end {align} \]

À l'aide d'opérations vectorielles, nous pouvons réécrire l'équation \ ref {eq1}

\ [\ begin {align*} ⌘x−x_0, y−y_0, z−z_0⟩ &=ta-ta, tb, tc⟩ \ \ [4pt]
⌘x, y, z−⌘x_0, y_0, z_0⟩ &=t298 a, b, c⟩ \ \ [4 points]
 \ entretoise {⌘x, y, z⟩} _ {\ vecs {r}} &= \ entretoise {⟩ x_0, y_0, z_0⟩} _ {\ vecs {r} _o} +t \ entretoise {⟩ a, b, c⟩} _ {\ vecs {v}}. \ end {align*} \]

Réglage\( \vecs{r}=⟨x,y,z⟩\) et\( \vecs{r}_0=⟨x_0,y_0,z_0⟩\), nous avons maintenant l'équation vectorielle d'une droite :

\[ \vecs{r}=\vecs{r}_0+t\vecs{v}. \label{vector} \]

En assimilant les composants, l'équation \ ref {vector} montre que les équations suivantes sont simultanément vraies :\( x−x_0=ta, y−y_0=tb,\) et\( z−z_0=tc.\) si nous résolvons chacune de ces équations pour les variables des composantes\( x,y,\) et\( z\) que nous obtenons un ensemble d'équations dans lesquelles chaque variable est définie en termes de paramètre \(t\)et qui, ensemble, décrivent la ligne. Cet ensemble de trois équations forme un ensemble d'équations paramétriques d'une droite :

\[ x=x_0+ta \nonumber \]

\[ y=y_0+tb \nonumber \]

\[ z=z_0+tc.\nonumber \]

Si nous résolvons chacune des équations par\( t\) hypothèse\( a,b\) et que nous\( c\) ne sommes pas nulles, nous obtenons une description différente de la même droite :

\[ \begin{align*} \dfrac{x−x_0}{a} =t \\[4pt] \dfrac{y−y_0}{b} =t \\[4pt] \dfrac{z−z_0}{c} =t.\end{align*}\]

Comme chaque expression est égale\(t\), elles ont toutes la même valeur. Nous pouvons les mettre égaux les uns aux autres pour créer des équations symétriques d'une droite :

\[\dfrac{x−x_0}{a}=\dfrac{y−y_0}{b}=\dfrac{z−z_0}{c}. \nonumber \]

Nous résumons les résultats dans le théorème suivant.

Théorème : équations paramétriques et symétriques d'une droite

Une droite\( L\) parallèle au vecteur\( \vecs{v}=⟨a,b,c⟩\) et passant par un point\( P(x_0,y_0,z_0)\) peut être décrite par les équations paramétriques suivantes :

\[ x=x_0+ta, y=y_0+tb, \nonumber \]

et

\[ z=z_0+tc. \nonumber \]

Si les constantes\( a,b,\) et les valeurs\( c\) sont toutes différentes de zéro, elles\( L\) peuvent être décrites par l'équation symétrique de la droite :

\[\dfrac{x−x_0}{a}=\dfrac{y−y_0}{b}=\dfrac{z−z_0}{c}. \nonumber \]

Les équations paramétriques d'une droite ne sont pas uniques. L'utilisation d'un vecteur parallèle différent ou d'un point différent sur la ligne permet d'obtenir une représentation différente et équivalente. Chaque ensemble d'équations paramétriques mène à un ensemble apparenté d'équations symétriques, de sorte qu'une équation symétrique d'une droite n'est pas non plus unique.

Exemple\( \PageIndex{1}\): Equations of a Line in Space

Trouvez des équations paramétriques et symétriques de la droite passant par des points\( (1,4,−2)\) et\( (−3,5,0).\)

Solution

Tout d'abord, identifiez un vecteur parallèle à la ligne :

\[ \vecs v=⟨−3−1,5−4,0−(−2)⟩=⟨−4,1,2⟩. \nonumber \]

Utilisez l'un des points indiqués sur la ligne pour compléter les équations paramétriques :

\[\begin{align*} x =1−4t \\[4pt] y =4+t, \end{align*}\]

et

\[ z=−2+2t. \nonumber \]

Résolvez chaque équation\( t\) pour créer l'équation symétrique de la droite :

\[ \dfrac{x−1}{−4}=y−4=\dfrac{z+2}{2}. \nonumber \]

Exercice\( \PageIndex{1}\)

Trouvez des équations paramétriques et symétriques de la droite passant par des points\( (1,−3,2)\) et\( (5,−2,8).\)

Astuce :

Commencez par trouver un vecteur parallèle à la ligne.

Réponse

Ensemble possible d'équations paramétriques : ensemble\( x=1+4t,\; y=−3+t,\; z=2+6t;\) connexe d'équations symétriques :\[ \dfrac{x−1}{4}=y+3=\dfrac{z−2}{6} \nonumber \]

Parfois, nous ne voulons pas l'équation d'une droite entière, juste un segment de droite. Dans ce cas, nous limitons les valeurs de notre paramètre\( t\). Par exemple, laissez\( P(x_0,y_0,z_0)\) et\( Q(x_1,y_1,z_1)\) soyez des points sur une ligne et laissez\( \vecs p=⟨x_0,y_0,z_0⟩\) et\( \vecs q=⟨x_1,y_1,z_1⟩\) soyez les vecteurs de position associés. De plus, laissez\(\vecs r=⟨x,y,z⟩\). Nous voulons trouver une équation vectorielle pour le segment de droite compris entre\( P\) et\( Q\). En utilisant\( P\) comme point connu sur la ligne et\( \vecd{PQ}=⟨x_1−x_0,y_1−y_0,z_1−z_0⟩\) comme équation du vecteur de direction, l'équation \ ref {vector} donne

\[\vecs{r}=\vecs{p}+t(\vecd{PQ}). \label{eq10} \]

L'équation \ ref {eq10} peut être étendue à l'aide des propriétés des vecteurs :

\ [\ begin {align*} \ vecs {r} &= \ vecs {p} +t (\ vecd {PQ}) \ \ [4 points]
&=⌘x_0, y_0, z_0+t⌘x_1−x_0, y_1−y_0, z_1−z_0⟩ \ \ [4 points]
&=rigix_0, y_0, z_0+t (⌘x_1, y_1, z_1−␞ x_0, y_0, z_0⟩) \ \ [4 points]
&=⌘x_0, y_0, z_0+trq−x_1, y_1, z_1−tchacx_0, y_0, z_0⟩ \ \ [4 points]
& =( 1−t−1 t) ctrl+x_0, y_0 , z_0+trqx_1, y_1, z_1⟩ \ \ [4 points]
& =( 1−t) \ vecs {p} +t \ vecs {q}. \ end {align*} \]

Ainsi, l'équation vectorielle de la droite passant par\( P\) et\( Q\) est

\[\vecs{r}=(1−t)\vecs{p}+t\vecs{q}. \nonumber \]

N'oubliez pas que nous ne voulions pas l'équation de la droite entière, juste le segment de droite entre\( P\) et\( Q\). Remarquez que quand\( t=0\), nous l'avons fait\(\vecs{r}=\vecs{p}\) et quand\( t=1\), nous l'avons fait\( \vecs r=\vecs q\). Par conséquent, l'équation vectorielle du segment de droite entre\( P\) et\( Q\) est

\[\vecs{r}=(1−t)\vecs{p}+t\vecs{q},0≤t≤1. \nonumber \]

Pour en revenir à l'équation \ ref {vector}, nous pouvons également trouver des équations paramétriques pour ce segment de droite. Nous avons

\ [\ begin {align*} \ vecs {r} &= \ vecs {p} +t (\ vecd {PQ}) \ \ [4 points]
⌘x, y, z⟩ &=⌘x_0, y_0, z_0+t⌘x_1−x_0, y_1−y_0, z_1−z_0⟩ \ \ [4 points]
&=_0+t (x_1−x_0), y_0+t (y_1−y_0), z_0+t (z_1−z_0) ⟩. \ end {align*} \]

Ensuite, les équations paramétriques sont

\[ \begin{align*} x &=x_0+t(x_1−x_0) \\[4pt] y &=y_0+t(y_1−y_0) \\[4pt] z &=z_0+t(z_1−z_0), \quad 0≤t≤1. \end{align*} \label{para} \]

Exemple\( \PageIndex{2}\): Parametric Equations of a Line Segment

Trouvez des équations paramétriques du segment de droite entre les points\( P(2,1,4)\) et\( Q(3,−1,3).\)

Solution

Commencez par les équations paramétriques d'une droite (Equations \ ref {para}) et travaillez avec chaque composant séparément :

\[ \begin{align*} x &=x_0+t(x_1−x_0)\\[4pt] &=2+t(3−2)\\[4pt] &=2+t, \end{align*}\]

\[ \begin{align*} y &=y_0+t(y_1−y_0)\\[4pt] &=1+t(−1−1)\\[4pt] &=1−2t, \end{align*}\]

et

\[ \begin{align*} z &=z_0+t(z_1−z_0)\\[4pt] &=4+t(3−4)\\[4pt] &=4−t. \end{align*}\]

Par conséquent, les équations paramétriques pour le segment de droite sont

\[ \begin{align*} x &=2+t\\[4pt] y &=1−2t\\[4pt] z &=4−t,\quad 0≤t≤1.\end{align*}\]

Exercice\( \PageIndex{2}\)

Trouvez des équations paramétriques du segment de droite entre les points\( P(−1,3,6)\) et\( Q(−8,2,4)\).

Réponse

\( x=−1−7t,\; y=3−t,\; z=6−2t, \quad 0≤t≤1 \)

Distance entre un point et une ligne

Nous savons déjà comment calculer la distance entre deux points de l'espace. Nous étendons maintenant cette définition pour décrire la distance entre un point et une ligne dans l'espace. Il existe plusieurs contextes réels dans lesquels il est important de pouvoir calculer ces distances. Lors de la construction d'une maison, par exemple, les constructeurs doivent tenir compte des exigences de « recul », lorsque les structures ou les accessoires doivent se trouver à une certaine distance de la limite de la propriété. Le transport aérien offre un autre exemple. Les compagnies aériennes s'inquiètent des distances entre les zones peuplées et des trajectoires de vol proposées.

\( L\)Soit une ligne dans le plan et\( M\) soit n'importe quel point ne se trouvant pas sur la ligne. Ensuite, nous définissons la\( d\) distance\( M\) entre et\( L\) comme la longueur du segment de ligne\( \overline{MP}\), où se\( P\)\( \overline{MP}\) trouve un point perpendiculaire à\( L\) (Figure\(\PageIndex{2}\)).\( L\)

Figure\(\PageIndex{2}\) : La distance entre un point\( M\) et une ligne\( L\) est la longueur de\( \overline{MP}\).

Lorsque nous recherchons la distance entre une ligne et un point dans l'espace, la figure s'applique\(\PageIndex{2}\) toujours. Nous définissons toujours la distance comme la longueur du segment de ligne perpendiculaire reliant le point à la ligne. Dans l'espace, cependant, il n'existe aucun moyen clair de savoir quel point de la ligne crée un tel segment de ligne perpendiculaire. Nous sélectionnons donc un point arbitraire sur la ligne et utilisons les propriétés des vecteurs pour calculer la distance. Par conséquent,\( P\) soit un point arbitraire sur la ligne\( L\) et\(\vecs{v}\) soit un vecteur de direction pour\( L\) (Figure\(\PageIndex{3}\)).

Figure\(\PageIndex{3}\) : Les vecteurs\( \vecd{PM}\) et\( \vecs{v}\) forment les deux côtés d'un parallélogramme avec base\( ‖\vecs v‖\) et hauteur\( d\), qui est la distance entre une ligne et un point dans l'espace.

Vecteurs\( \vecd{PM}\) et\(\vecs{v}\) forment les deux côtés d'un parallélogramme avec une surface\( ‖\vecd{PM}×\vecs{v}‖\). À l'aide d'une formule issue de la géométrie, l'aire de ce parallélogramme peut également être calculée comme le produit de sa base et de sa hauteur :

\[‖\vecd{PM}×\vecs{v}‖=‖\vecs v‖d. \nonumber \]

Nous pouvons utiliser cette formule pour trouver une formule générale pour la distance entre une ligne dans l'espace et tout point ne se trouvant pas sur la ligne.

Distance entre un point et une ligne

\( L\)Soit une ligne dans l'espace passant par un point\( P\) avec un vecteur de direction\(\vecs{v}\). S'il\( M\) y a un point qui n'est pas allumé\( L\), alors la distance entre\( M\) et\( L\) est

\[d=\dfrac{‖\vecd{PM}×\vecs{v}‖}{‖\vecs{v}‖}. \nonumber \]

Exemple\( \PageIndex{3}\): Calculating the Distance from a Point to a Line

Trouvez la distance entre le point\( M=(1,1,3)\) et la ligne\( \dfrac{x−3}{4}=\dfrac{y+1}{2}=z−3.\)

Solution :

À partir des équations symétriques de la droite, nous savons que le vecteur\( \vecs{v}=⟨4,2,1⟩\) est un vecteur de direction pour la droite. Si les équations symétriques de la droite sont égales à zéro, nous voyons que le point\( P(3,−1,3)\) se trouve sur la droite. Ensuite,

\[\begin{align*} \vecd{PM} =⟨1−3,1−(−1),3−3⟩\\[4pt] =⟨−2,2,0⟩. \end{align*}\]

Pour calculer la distance, nous devons trouver\( \vecd{PM}×\vecs v:\)

\ [\ begin {align*} \ vecd {PM} × \ vecs {v} &= \ begin {vmatrix} \ mathbf {\ hat i} & \ mathbf {\ hat j} & \ mathbf {\ hat k} \ \ −2 et 2 et 0 \ \ 4 et 2 et 1 \ end {vmatrix} \ \ [4pt] &= (2−0) \ mathbf f {\ hat i} − (−2−0) \ mathbf {\ hat j} + (−4−8) \ mathbf {\ hat k} \ \ [4 points]
&=2 \ mathbf {\ hat i} +2 \ mathbf {\ hat j} −12 \ mathbf {\ hat k}. \ end {align*} \]

Par conséquent, la distance entre le point et la ligne est (Figure\(\PageIndex{4}\))

\ [\ begin {align*} d &= \ dfrac {] \ vecd {PM} × \ vecs {v}} {#1 \ vecs {v}} \ \ [4 points]
&= \ dfrac {\ sqrt {2^2+2^2+12^2}} {\ sqrt {4^2+2^2+1^2}} \ \ [4 points]
&= \ dfrac {2 \ sqrt {38}} {\ sqrt {21}} \ \ [4 points]
&= \ dfrac {2 \ sqrt {798}} {21} \, \ text {unités} \ end {align*} \]

Figure\(\PageIndex{4}\) :\( (1,1,3)\) Le point est approximativement à\( 2.7\) des unités de la ligne avec des équations symétriques\( \dfrac{x−3}{4}=\dfrac{y+1}{2}=z−3.\)

Exercice\( \PageIndex{3}\)

Trouvez la distance entre le point\( (0,3,6)\) et la droite à l'aide d'équations paramétriques\( x=1−t,\; y=1+2t,\; z=5+3t.\)

Allusion

Trouvez un vecteur avec un point initial\( (0,3,6)\) et un point terminal sur la ligne, puis recherchez un vecteur de direction pour la ligne.

Réponse

\( \sqrt{\dfrac{10}{7}} = \dfrac{\sqrt{70}}{7} \,\text{units} \)

Relations entre les lignes

À partir de deux lignes dans le plan bidimensionnel, les lignes sont égales, elles sont parallèles mais pas égales, ou elles se croisent en un seul point. En trois dimensions, un quatrième cas est possible. Si deux lignes dans l'espace ne sont pas parallèles mais ne se croisent pas, elles sont considérées comme des lignes obliques (Figure\(\PageIndex{5}\)).

Figure\(\PageIndex{5}\) : En trois dimensions, il est possible que deux lignes ne se croisent pas, même lorsqu'elles ont des directions différentes.

Pour classer les lignes comme étant parallèles mais pas égales, égales, croisées ou inclinées, nous devons savoir deux choses : si les vecteurs de direction sont parallèles et si les lignes partagent un point (Figure\(\PageIndex{6}\)).

Figure\(\PageIndex{6}\) : Déterminez la relation entre deux lignes en fonction du fait que leurs vecteurs de direction sont parallèles et qu'elles partagent un point.

Exemple\( \PageIndex{4}\): Classifying Lines in Space

Pour chaque paire de lignes, déterminez si les lignes sont égales, parallèles mais non égales, inclinées ou croisées.

un.

• \( L_1:\; x=2s−1, \; y=s−1, \; z=s−4\)
• \( L_2: \; x=t−3, \; y=3t+8, \; z=5−2t\)

b.

• \( L_1: \; x=−y=z\)
• \( L_2:\; \dfrac{x−3}{2}=y=z−2\)

c.

• \( L_1:\; x=6s−1,\; y=−2s,\; z=3s+1\)
• \( L_2:\; \dfrac{x−4}{6}=\dfrac{y+3}{−2}=\dfrac{z−1}{3}\)

Solution

a.\( L_1\) La ligne a un vecteur de direction\( \vecs v_1=⟨2,1,1⟩\) ; la ligne\( L_2\) a un vecteur de direction\( \vecs v_2=⟨1,3,−2⟩\). Comme les vecteurs de direction ne sont pas des vecteurs parallèles, les lignes se croisent ou sont inclinées. Pour déterminer si les lignes se croisent, nous voyons s'il existe un point\( (x,y,z)\), qui se trouve sur les deux lignes. Pour trouver ce point, nous utilisons les équations paramétriques pour créer un système d'égalités :

\[ 2s−1=t−3; \nonumber \]

\[ s−1=3t+8; \nonumber \]

\[ s−4=5−2t. \nonumber \]

Selon la première équation, la\( t=2s+2.\) substitution dans la deuxième équation donne

\( s−1=3(2s+2)+8\)

\( s−1=6s+6+8\)

\( 5s=−15\)

\( s=−3.\)

La substitution dans la troisième équation donne toutefois lieu à une contradiction :

\( s−4=5−2(2s+2)\)

\( s−4=5−4s−4\)

\( 5s=5\)

\( s=1.\)

Aucun point ne satisfait les équations paramétriques pour\( L_1\) et\( L_2\) simultanément. Ces lignes ne se croisent pas, elles sont donc inclinées (voir la figure suivante).

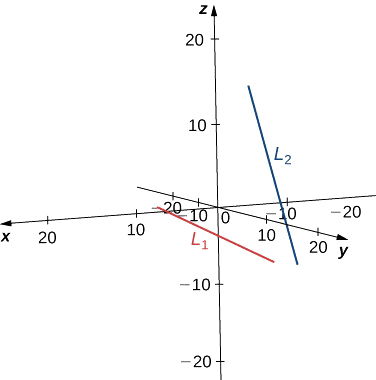
b.\( L_1\) La ligne a un vecteur de direction\( \vecs v_1=⟨1,−1,1⟩\) et passe par l'origine,\( (0,0,0)\). \( L_2\)La ligne a un vecteur de direction différent\( \vecs v_2=⟨2,1,1⟩\), de sorte que ces lignes ne sont ni parallèles ni égales. \( r\)Représentent le paramètre pour la ligne\( L_1\) et\(s\) représentons le paramètre pour\( L_2\) :

\[\begin{align*} &\text{Line }L_1: & & \text{Line }L_2:\\[4pt] &x = r & & x = 2s + 3\\[4pt] &y = -r & & y = s \\[4pt] &z = r & & z = s + 2 \end{align*}\]

Résolvez le système d'équations pour trouver\( r=1\) et\( s=−1\). Si nous avons besoin de trouver le point d'intersection, nous pouvons remplacer ces paramètres dans les équations d'origine pour obtenir\( (1,−1,1)\) (voir la figure suivante).

c. Lignes\( L_1\) et\( L_2\) vecteurs de direction équivalents :\( \vecs v=⟨6,−2,3⟩.\) Ces deux lignes sont parallèles (voir la figure suivante).

Exercice\( \PageIndex{4}\)

Décrivez la relation entre les droites à l'aide des équations paramétriques suivantes :

\[ x=1−4t, \; y=3+t, \; z=8−6t \nonumber \]

\[x=2+3s,\; y=2s,\; z=−1−3s. \nonumber \]

Allusion

Commencez par identifier les vecteurs de direction pour chaque ligne. L'un est-il un multiple de l'autre ?

Réponse

Ces lignes sont asymétriques car leurs vecteurs de direction ne sont pas parallèles et aucun point ne\( (x,y,z)\) se trouve sur les deux lignes.

Équations pour un plan

Nous savons qu'une ligne est déterminée par deux points. En d'autres termes, pour deux points distincts, il existe exactement une ligne qui passe par ces points, que ce soit en deux dimensions ou en trois dimensions. De même, étant donné que trois points ne se trouvent pas tous sur la même ligne, il existe un plan unique qui passe par ces points. Tout comme une ligne est déterminée par deux points, un plan est déterminé par trois.

C'est peut-être la façon la plus simple de caractériser un avion, mais nous pouvons également utiliser d'autres descriptions. Par exemple, étant donné que deux lignes distinctes se croisent, il existe exactement un plan contenant les deux lignes. Un plan est également déterminé par une ligne et tout point qui ne se trouve pas sur la ligne. Ces caractérisations découlent naturellement de l'idée qu'un plan est déterminé par trois points. Peut-être que la caractérisation la plus surprenante d'un avion est en fait la plus utile.

Imaginez une paire de vecteurs orthogonaux qui partagent un point initial. Visualisez que vous saisissez l'un des vecteurs et que vous le tordez. Au fur et à mesure que vous tournez, l'autre vecteur tourne et balaie un plan. Ici, nous décrivons ce concept mathématiquement. \(\vecs{n}=⟨a,b,c⟩\)Soyons un vecteur et\(P=(x_0,y_0,z_0)\) un point. Ensuite, l'ensemble de tous les points\(Q=(x,y,z)\) tels qu'\(\vecd{PQ}\)ils sont orthogonaux à\(\vecs{n}\) forme un plan (Figure\(\PageIndex{7}\)). Nous disons que\(\vecs{n}\) c'est un vecteur normal, ou perpendiculaire au plan. N'oubliez pas que le produit scalaire des vecteurs orthogonaux est nul. Ce fait génère l'équation vectorielle d'un plan :

\[\vecs{n}⋅\vecd{PQ}=0. \nonumber \]

La réécriture de cette équation fournit des moyens supplémentaires de décrire le plan :

\[ \begin{align*} \vecs{n}⋅\vecd{PQ} &=0 \\[4pt] ⟨a,b,c⟩⋅⟨x−x_0,y−y_0,z−z_0⟩ &=0 \\[4pt] a(x−x_0)+b(y−y_0)+c(z−z_0) &=0. \end{align*}\]

Figure\(\PageIndex{7}\) : À partir d'un point\(P\) et d'un vecteur\(\vecs{n}\), l'ensemble de tous les points\(Q\)\(\vecd{PQ}\) orthogonaux à\(\vecs{n}\) forme un plan.

Définition : Équation scalaire d'un plan

À partir d'un point\(P\) et d'un vecteur\(\vecs n\), l'ensemble de tous les points\(Q\) répondant à l'équation\(\vecs n⋅\vecd{PQ}=0\) forme un plan. L'équation

\[\vecs{n}⋅\vecd{PQ}=0 \nonumber \]

est connue sous le nom d'équation vectorielle d'un plan.

L'équation scalaire d'un plan (parfois aussi appelée équation standard d'un plan) contenant un point\(P=(x_0,y_0,z_0)\) avec un vecteur normal\(\vec{n}=⟨a,b,c⟩\) est

\[a(x−x_0)+b(y−y_0)+c(z−z_0)=0. \nonumber \]

Cette équation peut être exprimée comme\(ax+by+cz+d=0,\) suit :\(d=−ax_0−by_0−cz_0.\) Cette forme de l'équation est parfois appelée forme générale de l'équation d'un plan.

Comme décrit précédemment dans cette section, trois points qui ne se trouvent pas tous sur la même ligne déterminent un plan. Étant donné trois de ces points, nous pouvons trouver une équation pour le plan contenant ces points.

Exemple\(\PageIndex{5}\): Writing an Equation of a Plane Given Three Points in the Plane

Écrivez une équation pour le plan contenant\(P=(1,1,−2), Q=(0,2,1),\) des points,\(R=(−1,−1,0)\) sous une forme standard et générale.

Solution

Pour écrire une équation pour un plan, nous devons trouver un vecteur normal pour le plan. Nous commençons par identifier deux vecteurs dans le plan :

\[ \begin{align*} \vecd{PQ} &=⟨0−1,2−1,1−(−2)⟩\\[4pt] &=⟨−1,1,3⟩ \\[4pt] \vecd{QR} &=⟨−1−0,−1−2,0−1⟩\\[4pt] &=⟨−1,−3,−1⟩.\end{align*}\]

Le produit croisé\(\vecd{PQ}×\vecd{QR}\) est orthogonal aux deux\(\vecd{PQ}\) et\(\vecd{QR}\) est donc normal au plan qui contient ces deux vecteurs :

\[ \begin{align*} \vecs n &=\vecd{PQ}×\vecd{QR} \\[4pt] &=\begin{vmatrix}\mathbf{\hat i} & \mathbf{\hat j} & \mathbf{\hat k}\\−1 & 1 & 3\\−1 & −3 & −1\end{vmatrix} \\[4pt] &=(−1+9)\mathbf{\hat i}−(1+3)\mathbf{\hat j}+(3+1)\mathbf{\hat k} \\[4pt] &= 8\mathbf{\hat i}−4\mathbf{\hat j}+4\mathbf{\hat k}.\end{align*}\]

Ainsi,\(\vecs n=⟨8,−4,4⟩,\) et nous pouvons choisir n'importe lequel des trois points donnés pour écrire une équation du plan :

\[ \begin{align*} 8(x−1)−4(y−1)+4(z+2) &=0 \\[4pt] 8x−4y+4z+4 &=0. \end{align*}\]

Les équations scalaires d'un plan varient en fonction du vecteur normal et du point choisis.

Exemple\(\PageIndex{6}\): Writing an Equation for a Plane Given a Point and a Line

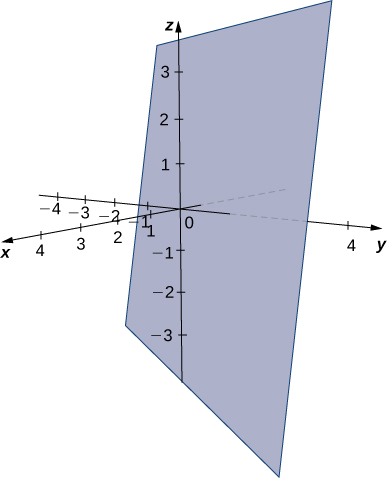
Trouvez une équation du plan qui passe par le point\((1,4,3)\) et contient la droite donnée par\(x=\dfrac{y−1}{2}=z+1.\)

Solution

Les équations symétriques décrivent la droite qui passe par un point\((0,1,−1)\) parallèlement au vecteur\(\vecs v_1=⟨1,2,1⟩\) (voir la figure suivante). Utilisez ce point et le point donné\((1,4,3),\) pour identifier un second vecteur parallèle au plan :

\[ \vecs v_2=⟨1−0,4−1,3−(−1)⟩=⟨1,3,4⟩. \nonumber \]

Utilisez le produit croisé de ces vecteurs pour identifier un vecteur normal pour le plan :

\[ \begin{align*} \vecs n &=\vecs v_1×\vecs v_2 \nonumber \\[4pt] &=\begin{vmatrix}\mathbf{\hat i} & \mathbf{\hat j} & \mathbf{\hat k}\\1 & 2 & 1\\1 & 3 & 4\end{vmatrix} \nonumber \\[4pt] &=(8−3)\mathbf{\hat i}−(4−1)\mathbf{\hat j}+(3−2)\mathbf{\hat k} \\[4pt] &=5\mathbf{\hat i}−3\mathbf{\hat j}+\mathbf{\hat k}. \nonumber\end{align*}\]

Les équations scalaires du plan sont\(5x−3(y−1)+(z+1)=0\) et\(5x−3y+z+4=0.\)

Exercice\(\PageIndex{6}\)

Trouvez une équation du plan contenant les droites\(L_1\) et\(L_2\) :

\[ L_1: \; x=−y=z \nonumber \]

\[ L_2:\; \dfrac{x−3}{2}=y=z−2. \nonumber \]

Allusion

Conseil : Le produit croisé des vecteurs directeurs des lignes donne un vecteur normal pour le plan.

Réponse

\[ −2(x−1)+(y+1)+3(z−1)=0 \nonumber \]

ou

\[ −2x+y+3z=0 \nonumber \]

Maintenant que nous pouvons écrire une équation pour un plan, nous pouvons utiliser l'équation pour trouver la distance\(d\) entre un point\(P\) et le plan. Elle est définie comme la distance la plus courte possible entre\(P\) un point du plan et un point.

Figure\(\PageIndex{8}\) : Nous voulons trouver la distance la plus courte entre le point P et le plan. \(R\)Soit point le point du plan tel que, pour tout autre point du plan\(Q, ‖\vecd{RP}‖<‖\vecd{QP}‖\).

Tout comme nous trouvons la distance bidimensionnelle entre un point et une ligne en calculant la longueur d'un segment de droite perpendiculaire à la ligne, nous trouvons la distance tridimensionnelle entre un point et un plan en calculant la longueur d'un segment de ligne perpendiculaire au plan. \(R\)Soit le point du plan qui\(\vecd{RP}\) est orthogonal au plan, et\(Q\) soit un point arbitraire dans le plan. Ensuite, la projection du vecteur\(\vecd{QP}\) sur le vecteur normal décrit le vecteur\(\vecd{RP}\), comme indiqué sur la figure\(\PageIndex{8}\).

La distance entre un plan et un point

Supposons qu'un plan avec un vecteur normal\(\vecs{n}\) passe par un point\(Q\). La\(d\) distance entre le plan et un point qui ne se trouve\(P\) pas dans le plan est donnée par

\[d=‖\text{proj}_\vecs{n}\,\vecd{QP}‖=∣\text{comp}_\vecs{n}\, \vecd{QP}∣=\dfrac{∣\vecd{QP}⋅\vecs{n}∣}{‖\vecs{n}‖}. \label{distanceplanepoint} \]

Exemple\(\PageIndex{7}\): Distance between a Point and a Plane

Détermine la distance entre le point\(P=(3,1,2)\) et le plan indiqué par\(x−2y+z=5\) (voir la figure suivante).

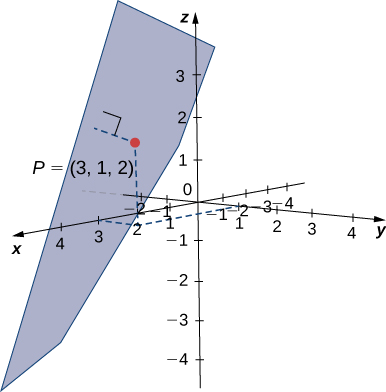
Solution

Les coefficients de l'équation du plan fournissent un vecteur normal pour le plan :\(\vecs{n}=⟨1,−2,1⟩\). Pour trouver un vecteur\(\vecd{QP}\), nous avons besoin d'un point dans le plan. N'importe quel point fonctionnera, alors préparez-vous\(y=z=0\) à voir que ce point\(Q=(5,0,0)\) se trouve dans le plan. Trouvez la forme du composant du vecteur de\(Q\) à\(P\) :

\[ \vecd{QP}=⟨3−5,1−0,2−0⟩=⟨−2,1,2⟩. \nonumber \]

Appliquez la formule de distance de l'équation \ ref {distanceplanepoint} :

\[\begin{align*} d &=\dfrac{∣\vecd{QP}⋅\vecs n|}{‖\vecs n‖} \\[4pt] &=\dfrac{|⟨−2,1,2⟩⋅⟨1,−2,1⟩|}{\sqrt{1^2+(−2)^2+1^2}} \\[4pt] &=\dfrac{|−2−2+2|}{\sqrt{6}} \\[4pt] &=\dfrac{2}{\sqrt{6}} = \dfrac{\sqrt{6}}{3}\,\text{units}. \end{align*}\]

Exercice\(\PageIndex{7}\)

Détermine la distance entre le point\(P=(5,−1,0)\) et le plan indiqué par\(4x+2y−z=3\).

Allusion

Le point\((0,0,−3)\) se trouve dans l'avion.

Réponse

\[ \dfrac{15}{\sqrt{21}} = \dfrac{5\sqrt{21}}{7}\,\text{units} \nonumber \]

Plans parallèles et intersectés

Nous avons discuté des différentes relations possibles entre deux lignes en deux dimensions et en trois dimensions. Lorsque nous décrivons la relation entre deux plans dans l'espace, nous n'avons que deux possibilités : les deux plans distincts sont parallèles ou se croisent. Lorsque deux plans sont parallèles, leurs vecteurs normaux sont parallèles. Lorsque deux plans se croisent, l'intersection est une ligne (Figure\(\PageIndex{9}\)).

Figure\(\PageIndex{9}\) : L'intersection de deux plans non parallèles est toujours une ligne.

Nous pouvons utiliser les équations des deux plans pour trouver des équations paramétriques pour la ligne d'intersection.

Exemple\(\PageIndex{8}\): Finding the Line of Intersection for Two Planes

Trouvez des équations paramétriques et symétriques pour la droite formée par l'intersection des plans donnés par\(x+y+z=0\) et\(2x−y+z=0\) (voir la figure suivante).

Solution

Notez que les deux plans ont des normales non parallèles, de sorte que les plans se croisent. De plus, l'origine satisfait chaque équation, de sorte que nous savons que la ligne d'intersection passe par l'origine. Ajoutez les équations du plan afin d'éliminer l'une des variables, dans ce cas\(y\) :

\(x+y+z=0\)

\(2x−y+z=0\)

________________

\(3x+2z=0\).

Cela nous donne\(x=−\dfrac{2}{3}z.\) Nous substituons cette valeur dans la première équation pour l'exprimer\(y\) en termes de\(z\) :

\[ \begin{align*} x+y+z =0 \\[4pt] −\dfrac{2}{3}z+y+z =0 \\[4pt] y+\dfrac{1}{3}z =0 \\[4pt] y =−\dfrac{1}{3}z \end{align*}. \nonumber \]

Nous avons maintenant les deux premières variables\(x\) et\(y\), en ce qui concerne la troisième variable,\(z\). Nous définissons maintenant\(z\) en termes de\(t\). Pour éliminer le besoin de fractions, nous avons choisi de définir le paramètre\(t\) comme\(t=−\dfrac{1}{3}z\). Ensuite,\(z=−3t\). En substituant la représentation paramétrique de\(z\) back dans les deux autres équations, nous voyons que les équations paramétriques pour la ligne d'intersection sont\(x=2t, \; y=t, \; z=−3t.\) Les équations symétriques de la droite sont\(\dfrac{x}{2}=y=\dfrac{z}{−3}\).

Exercice\(\PageIndex{8}\)

Trouvez des équations paramétriques pour la droite formée par l'intersection de plans\(x+y−z=3\) et\(3x−y+3z=5.\)

Allusion

Ajoutez les deux équations, puis\(z\) exprimez-les en termes de\(x\). Ensuite, exprimez\(y\) en termes de\(x\).

Réponse

\( x=t, \; y=7−3t,\; z=4−2t\)

En plus de trouver l'équation de la ligne d'intersection entre deux plans, nous pouvons avoir besoin de trouver l'angle formé par l'intersection de deux plans. Par exemple, les constructeurs qui construisent une maison doivent connaître l'angle de rencontre des différentes sections du toit pour savoir si le toit sera beau et s'il sera bien drainé. Nous pouvons utiliser des vecteurs normaux pour calculer l'angle entre les deux plans. Nous pouvons le faire parce que l'angle entre les vecteurs normaux est le même que l'angle entre les plans. La figure\(\PageIndex{10}\) montre pourquoi cela est vrai.

Figure\(\PageIndex{10}\) : L'angle entre deux plans a la même mesure que l'angle entre les vecteurs normaux des plans.

Nous pouvons déterminer la mesure de l'angle\(θ\) entre deux plans qui se croisent en déterminant d'abord le cosinus de l'angle, à l'aide de l'équation suivante :

\[\cos θ=\dfrac{|\vecs{n}_1⋅\vecs{n}_2|}{‖\vecs{n}_1‖‖\vecs{n}_2‖}. \nonumber \]

Nous pouvons ensuite utiliser l'angle pour déterminer si deux plans sont parallèles ou orthogonaux ou s'ils se croisent selon un autre angle.

Exemple\(\PageIndex{9}\): Finding the Angle between Two Planes

Déterminez si chaque paire de plans est parallèle, orthogonale ou aucun des deux. Si les plans se croisent mais ne sont pas orthogonaux, déterminez la mesure de l'angle qui les sépare. Donnez la réponse en radians et arrondissez à deux décimales.

1. \(x+2y−z=8\)et\(2x+4y−2z=10\)
2. \(2x−3y+2z=3\)et\(6x+2y−3z=1\)
3. \(x+y+z=4\)et\(x−3y+5z=1\)

Solution :

1. Les vecteurs normaux pour ces plans sont\(\vecs{n}_1=⟨1,2,−1⟩\) et\(\vecs{n}_2=⟨2,4,−2⟩.\) Ces deux vecteurs sont des multiples scalaires l'un de l'autre. Les vecteurs normaux sont parallèles, donc les plans sont parallèles.
2. Les vecteurs normaux pour ces plans sont\(\vecs{n}_1=⟨2,−3,2⟩\) et\(\vecs{n}_2=⟨6,2,−3⟩\). En prenant le produit scalaire de ces vecteurs, nous avons\[\begin{align*} \vecs{n}_1⋅\vecs{n}_2 =⟨2,−3,2⟩⋅⟨6,2,−3⟩\\[4pt] =2(6)−3(2)+2(−3)=0.\end{align*} \nonumber \] Les vecteurs normaux sont orthogonaux, donc les plans correspondants sont également orthogonaux.
3. Les vecteurs normaux pour ces plans sont\(\vecs n_1=⟨1,1,1⟩\) et\(\vecs n_2=⟨1,−3,5⟩\) :\[\begin{align*} \cos θ &=\dfrac{|\vecs{n}_1⋅\vecs{n}_2|}{‖\vecs{n}_1‖‖\vecs{n}_2‖} \\[4pt] &=\dfrac{|⟨1,1,1⟩⋅⟨1,−3,5⟩|}{\sqrt{1^2+1^2+1^2}\sqrt{1^2+(−3)^2+5^2}} \\[4pt] &=\dfrac{3}{\sqrt{105}} \end{align*}\]
   Alors\(\theta =\arccos {\frac{3}{\sqrt{105}}} \approx 1.27\) rad.
   Ainsi, l'angle entre les deux plans est d'environ\(1.27\) rad, ou approximativement\(73°\).

Exercice\(\PageIndex{9}\)

Trouvez la mesure de l'angle entre les plans\(x+y−z=3\) et\(3x−y+3z=5.\) donnez la réponse en radians et arrondissez à deux décimales.

Allusion

Utilisez les coefficients des variables de chaque équation pour trouver un vecteur normal pour chaque plan.

Réponse

\( 1.44\, \text{rad} \)

Lorsque nous constatons que deux plans sont parallèles, nous pouvons avoir besoin de trouver la distance qui les sépare. Pour trouver cette distance, il suffit de sélectionner un point dans l'un des plans. La distance entre ce point et l'autre plan est la distance entre les plans.

Précédemment, nous avons introduit la formule pour calculer cette distance dans l'équation \ ref {distanceplanepoint} :

\[d=\dfrac{\vecd{QP}⋅\vecs{n}}{‖\vecs{n}‖}, \nonumber \]

où\(Q\) est un point sur le plan,\(P\) est un point qui ne se trouve pas dans le plan et\(\vec{n}\) est le vecteur normal qui passe par le point\(Q\). Tenez compte de la distance entre un point\((x_0,y_0,z_0)\) et un plan.\(ax+by+cz+k=0.\)\((x_1,y_1,z_1)\) Soit n'importe quel point du plan. La substitution dans la formule donne

\[\begin{align*}d =\dfrac{|a(x_0−x_1)+b(y_0−y_1)+c(z_0−z_1)|}{\sqrt{a^2+b^2+c^2}} \\[4pt] =\dfrac{|ax_0+by_0+cz_0+k|}{\sqrt{a^2+b^2+c^2}}.\end{align*}\]

Nous énonçons formellement ce résultat dans le théorème suivant.

Distance entre un point et un plan

\(P(x_0,y_0,z_0)\)Soyons un point. La distance entre le plan\(P\) et le plan\(ax+by+cz+k=0\) est donnée par

\[d=\dfrac{|ax_0+by_0+cz_0+k|}{\sqrt{a^2+b^2+c^2}}. \nonumber \]

Exemple\(\PageIndex{10}\): Finding the Distance between Parallel Planes

Détermine la distance entre les deux plans parallèles donnés par\(2x+y−z=2\) et\(2x+y−z=8.\)

Solution

Le point\((1,0,0)\) se trouve dans le premier plan. La distance souhaitée est donc

\[\begin{align*} d &=\dfrac{|ax_0+by_0+cz_0+k|}{\sqrt{a^2+b^2+c^2}} \\[4pt] &= \dfrac{|2(1)+1(0)+(−1)(0)+(−8)|}{\sqrt{2^2+1^2+(−1)^2}} \\[4pt] &= \dfrac{6}{\sqrt{6}}=\sqrt{6} \,\text{units} \end{align*}\]

Exercice\(\PageIndex{10}\):

Détermine la distance entre les plans parallèles\(5x−2y+z=6\) et\(5x−2y+z=−3\).

Allusion

Réglez\(x=y=0\) pour trouver un point sur le premier plan.

Réponse

\(\dfrac{9}{\sqrt{30}} = \dfrac{3\sqrt{30}}{10}\,\text{units} \)

Distance entre deux lignes obliques

Trouver la distance entre un point et une ligne ou entre une ligne et un plan semble être une procédure assez abstraite. Cependant, si les lignes représentent des tuyaux dans une usine chimique, des tubes dans une raffinerie de pétrole ou des routes à une intersection d'autoroutes, il peut être à la fois important et difficile de vérifier que la distance entre les deux lignes est conforme aux spécifications. L'une des solutions consiste à modéliser les deux tuyaux sous forme de lignes, à l'aide des techniques décrites dans ce chapitre, puis à calculer la distance qui les sépare. Le calcul consiste à former des vecteurs le long des directions des lignes et à utiliser à la fois le produit croisé et le produit scalaire.

Figure\(\PageIndex{11}\) : Les installations de tuyauterie industrielles comportent souvent des tuyaux circulant dans des directions différentes. Comment déterminer la distance entre deux tuyaux obliques ?

Les formes symétriques de deux lignes,\(L_1\) et\(L_2\), sont

\[L_1:\dfrac{x−x_1}{a_1}=\dfrac{y−y_1}{b_1}=\dfrac{z−z_1}{c_1} \nonumber \]

\[L_2:\dfrac{x−x_2}{a_2}=\dfrac{y−y_2}{b_2}=\dfrac{z−z_2}{c_2}. \nonumber \]

Vous devez développer une formule pour la distance\(d\) entre ces deux lignes, en termes de valeurs\(a_1,b_1,c_1;a_2,b_2,c_2;x_1,y_1,z_1;\) et\(x_2,y_2,z_2.\) La distance entre deux lignes est généralement considérée comme la distance minimale, il s'agit donc de la longueur d'un segment de ligne ou de la longueur d'un vecteur perpendiculaire aux deux lignes et croise les deux lignes.

1. Tout d'abord, notez deux vecteurs,\(\vecs{v}_1\) et\(\vecs{v}_2\), qui se trouvent le long de\(L_1\) et\(L_2\), respectivement.

2. Trouvez le produit croisé de ces deux vecteurs et appelez-le\(\vecs{N}\). Ce vecteur est perpendiculaire à\(\vecs{v}_1\) et\(\vecs{v}_2\), par conséquent, perpendiculaire aux deux lignes.

3. À partir d'un vecteur\(\vecs{N}\), formez un vecteur unitaire\(\vecs{n}\) dans la même direction.

4. Utilisez des équations symétriques pour trouver un vecteur\(\vecs{v}_{12}\) pratique situé entre deux points quelconques, un sur chaque ligne. Encore une fois, cela peut être fait directement à partir des équations symétriques.

5. Le produit scalaire de deux vecteurs est l'amplitude de la projection d'un vecteur sur l'autre, c'est-à-dire\(\vecs A⋅\vecs B=‖\vecs{A}‖‖\vecs{B}‖\cos θ,\) où\(θ\) est l'angle entre les vecteurs. À l'aide du produit scalaire, trouvez la projection du vecteur\(\vecs{v}_{12}\) trouvé dans l'étape\(4\) sur le vecteur unitaire\(\vecs{n}\) trouvé à l'étape\(3\). Cette projection est perpendiculaire aux deux lignes, et sa longueur doit donc être la distance perpendiculaire d qui les sépare. Notez que la valeur de\(d\) peut être négative, selon votre choix de vecteur\(\vecs{v}_{12}\) ou l'ordre du produit croisé. Utilisez donc des signes de valeur absolue autour du numérateur.

6. Vérifiez que votre formule donne la bonne distance\(|−25|/\sqrt{198}≈1.78\) entre les deux lignes suivantes :

\[L_1:\dfrac{x−5}{2}=\dfrac{y−3}{4}=\dfrac{z−1}{3} \nonumber \]

\[L_2:\dfrac{x−6}{3}=\dfrac{y−1}{5}=\dfrac{z}{7}. \nonumber \]

7. Votre expression générale est-elle valide lorsque les lignes sont parallèles ? Dans la négative, pourquoi pas ? (Conseil : que savez-vous de la valeur du produit croisé de deux vecteurs parallèles ? Où apparaîtrait ce résultat dans votre expression\(d\) ?)

8. Démontrez que l'expression de la distance est nulle lorsque les lignes se croisent. Rappelons que deux droites se croisent si elles ne sont pas parallèles et qu'elles se trouvent dans le même plan. Par conséquent, considérez la direction de\(\vecs{n}\) et\(\vecs{v}_{12}\). Quel est le résultat de leur produit scalaire ?

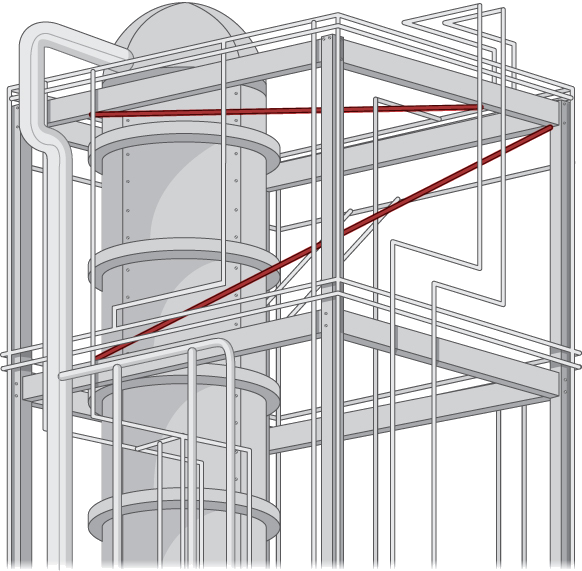
9. Envisagez l'application suivante. Les ingénieurs d'une raffinerie ont déterminé qu'ils devaient installer des entretoises entre de nombreuses conduites de gaz afin de réduire les vibrations dommageables. Pour minimiser les coûts, ils prévoient d'installer ces entretoises aux points les plus proches entre les tuyaux obliques adjacents. Comme ils disposent de schémas détaillés de la structure, ils sont en mesure de déterminer les longueurs correctes des entretoises nécessaires, et donc de les fabriquer et de les distribuer aux équipes d'installation sans perdre un temps précieux à effectuer des mesures.

La structure de cadre rectangulaire a les dimensions\(4.0×15.0×10.0\,\text{m}\) (hauteur, largeur et profondeur). Un secteur possède un tuyau qui entre dans le coin inférieur de l'unité de châssis standard et sort par le coin diamétralement opposé (celui qui est le plus éloigné en haut) ; appelez cela\(L_1\). Un deuxième tuyau entre et sort par les deux coins inférieurs opposés différents ; appelez ceci\(L_2\) (Figure\(\PageIndex{12}\)).

Figure\(\PageIndex{12}\) : Deux tuyaux traversent une unité de châssis standard.

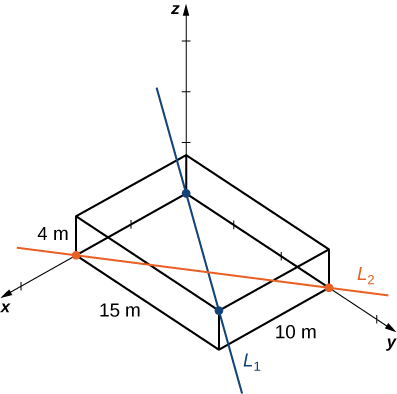
Notez les vecteurs le long des lignes représentant ces tuyaux, trouvez le produit croisé entre eux à partir duquel créer le vecteur unitaire\(\vecs n\), définissez un vecteur qui couvre deux points sur chaque ligne et déterminez enfin la distance minimale entre les lignes. (Prenez l'origine pour qu'elle se trouve dans le coin inférieur du premier tuyau.) De même, vous pouvez également développer les équations symétriques pour chaque droite et les remplacer directement dans votre formule.

Concepts clés

• En trois dimensions, la direction d'une ligne est décrite par un vecteur de direction. L'équation vectorielle d'une ligne dont le vecteur de direction\(\vecs v=⟨a,b,c⟩\) passe par le point\(P=(x_0,y_0,z_0)\) est\(\vecs r=\vecs r_0+t\vecs v\), où\(\vecs r_0=⟨x_0,y_0,z_0⟩\) est le vecteur de position du point\(P\). Cette équation peut être réécrite pour former les équations paramétriques de la droite :\(x=x_0+ta,y=y_0+tb\), et\(z=z_0+tc\). La droite peut également être décrite à l'aide des équations symétriques\(\dfrac{x−x_0}{a}=\dfrac{y−y_0}{b}=\dfrac{z−z_0}{c}\).
• \(L\)Soit une ligne dans l'espace passant par un point\(P\) avec un vecteur de direction\(\vecs v\). S'il\(Q\) y a un point qui n'est pas allumé\(L\), alors la distance entre\(Q\) et\(L\) est\(d=\dfrac{‖\vecd{PQ}×\vecs v‖}{‖\vecs v‖}.\)
• En trois dimensions, deux lignes peuvent être parallèles mais pas égales, égales, croisées ou inclinées.
• À partir d'un point\(P\) et d'un vecteur\(\vecs n\), l'ensemble de tous les points\(Q\) satisfaisant à l'équation\(\vecs n⋅\vecd{PQ}=0\) forme un plan. L'équation\(\vecs n⋅\vecd{PQ}=0\) est connue sous le nom d'équation vectorielle d'un plan.
• L'équation scalaire d'un plan contenant un point\(P=(x_0,y_0,z_0)\) avec un vecteur normal\(\vecs n=⟨a,b,c⟩\) est\(a(x−x_0)+b(y−y_0)+c(z−z_0)=0\). Cette équation peut être exprimée comme\(ax+by+cz+d=0,\) suit :\(d=−ax_0−by_0−cz_0.\) Cette forme de l'équation est parfois appelée forme générale de l'équation d'un plan.
• Supposons qu'un plan avec un vecteur normal\(n\) passe par un point\(Q\). La\(D\) distance entre le plan et un point qui\(P\) ne se trouve pas dans le plan est donnée par

\[D=‖\text{proj}_\vecs{n}\vecd{QP}‖=∣\text{comp}_\vecs{n}\vec{QP}∣=\dfrac{∣\vec{QP}⋅\vecs n∣}{‖\vecs n‖.} \nonumber \]

• Les vecteurs normaux des plans parallèles sont parallèles. Lorsque deux plans se croisent, ils forment une ligne.
• La mesure de l'angle\(θ\) entre deux plans qui se croisent peut être trouvée à l'aide de l'équation :\(\cos θ=\dfrac{|\vecs{n}_1⋅\vecs n_2|}{‖\vecs n_1‖‖\vecs n_2‖}\), où\(\vecs n_1\) et\(\vecs n_2\) sont des vecteurs normaux aux plans.
• La\(D\) distance entre le point\((x_0,y_0,z_0)\) et le plan\(ax+by+cz+d=0\) est donnée par

\[D=\dfrac{|a(x_0−x_1)+b(y_0−y_1)+c(z_0−z_1)|} {\sqrt{a^2+b^2+c^2}}=\dfrac{|ax_0+by_0+cz_0+d|}{\sqrt{a^2+b^2+c^2}} \nonumber \].

Équations clés

• Équation vectorielle d'une droite

\(\vecs r=\vecs r_0+t\vecs v\)

• Équations paramétriques d'une droite

\(x=x_0+ta,\; y=y_0+tb,\)et\(z=z_0+tc\)

• Équations symétriques d'une droite

\(\dfrac{x−x_0}{a}=\dfrac{y−y_0}{b}=\dfrac{z−z_0}{c}\)

• Équation vectorielle d'un plan

\(\vecs n⋅\vecd{PQ}=0\)

• Équation scalaire d'un plan

\(a(x−x_0)+b(y−y_0)+c(z−z_0)=0\)

• Distance entre un plan et un point

\(d=‖\text{proj}_\vecs{n}\vecd{QP}‖=∣\text{comp}_\vecs{n}\vecd{QP}∣=\dfrac{∣\vecd{QP}⋅\vecs n∣}{‖\vecs n‖}\)

Lexique

vecteur de direction

un vecteur parallèle à une ligne utilisé pour décrire la direction, ou l'orientation, de la ligne dans l'espace

forme générale de l'équation d'un plan

une équation sous la forme\(ax+by+cz+d=0,\) où\(\vecs n=⟨a,b,c⟩\) est un vecteur normal du plan,\(P=(x_0,y_0,z_0)\) est un point du plan, et\(d=−ax_0−by_0−cz_0\)

vecteur normal

un vecteur perpendiculaire à un plan

équations paramétriques d'une droite

l'ensemble d'équations\(x=x_0+ta, y=y_0+tb,\) et\(z=z_0+tc\) description de la ligne avec le vecteur de direction\(v=⟨a,b,c⟩\) passant par le point\((x_0,y_0,z_0)\)

équation scalaire d'un plan

l'équation\(a(x−x_0)+b(y−y_0)+c(z−z_0)=0\) utilisée pour décrire un plan contenant un point\(P=(x_0,y_0,z_0)\) avec un vecteur normal\(n=⟨a,b,c⟩\) ou sa forme alternative\(ax+by+cz+d=0\), où\(d=−ax_0−by_0−cz_0\)

lignes obliques

deux lignes qui ne sont pas parallèles mais qui ne se croisent pas

équations symétriques d'une droite

les équations\(\dfrac{x−x_0}{a}=\dfrac{y−y_0}{b}=\dfrac{z−z_0}{c}\) décrivant la droite dont le vecteur de direction\(v=⟨a,b,c⟩\) passe par le point\((x_0,y_0,z_0)\)

équation vectorielle d'une droite

l'équation\(\vecs r=\vecs r_0+t\vecs v\) utilisée pour décrire une ligne dont le vecteur de direction\(\vecs v=⟨a,b,c⟩\) passe par un point\(P=(x_0,y_0,z_0)\), où\(\vecs r_0=⟨x_0,y_0,z_0⟩\), est le vecteur de position du point\(P\)

équation vectorielle d'un plan

l'équation\(\vecs n⋅\vecd{PQ}=0,\) où\(P\) est un point donné dans le plan,\(Q\) est n'importe quel point du plan et\(\vecs n\) est un vecteur normal du plan