12.2 : Vecteurs en trois dimensions
- Page ID
- 197099
- Décrivez mathématiquement l'espace tridimensionnel.
- Localisez des points dans l'espace en utilisant des coordonnées
- Écrivez la formule de distance en trois dimensions.
- Écrivez les équations pour des plans et des sphères simples.
- Effectuez des opérations vectorielles dans\(\mathbb{R}^{3}\).
Les vecteurs sont des outils utiles pour résoudre des problèmes bidimensionnels. La vie, cependant, se déroule en trois dimensions. Pour étendre l'utilisation des vecteurs à des applications plus réalistes, il est nécessaire de créer un cadre pour décrire l'espace tridimensionnel. Par exemple, bien qu'une carte bidimensionnelle soit un outil utile pour naviguer d'un endroit à un autre, la topographie du terrain est importante dans certains cas. L'itinéraire que vous avez prévu traverse-t-il les montagnes ? Devez-vous traverser une rivière ? Pour apprécier pleinement l'impact de ces caractéristiques géographiques, vous devez utiliser trois dimensions. Cette section présente une extension naturelle du plan de coordonnées cartésien bidimensionnel en trois dimensions.
Systèmes de coordonnées tridimensionnels
Comme nous l'avons appris, le système de coordonnées rectangulaires bidimensionnelles contient deux axes perpendiculaires : l'\(x\)axe horizontal et l'\(y\)axe vertical. Nous pouvons ajouter une troisième dimension, l'\(z\)axe -, qui est perpendiculaire à la fois à l'\(x\)axe -et à l'\(y\)axe -. Nous appelons ce système le système de coordonnées rectangulaires tridimensionnelles. Il représente les trois dimensions que nous rencontrons dans la vie réelle.
Le système de coordonnées rectangulaires tridimensionnelles se compose de trois axes perpendiculaires : l'\(x\)axe\(y\) -, l'axe -et l'\(z\)axe -. Comme chaque axe est une ligne numérique représentant tous les nombres réels\(ℝ\), le système tridimensionnel est souvent désigné par\(ℝ^3\).
Sur la figure\(\PageIndex{1a}\), l'\(z\)axe positif est représenté au-dessus du plan contenant les\(y\) axes\(x\) - et. L'\(x\)axe positif apparaît à gauche et l'\(y\)axe positif à droite. Une question naturelle à se poser est la suivante : comment cet arrangement a-t-il été déterminé ? Le système affiché suit la règle de la main droite. Si nous prenons notre main droite et alignons les doigts sur l'\(x\)axe positif, puis que nous courbons les doigts de manière à ce qu'ils pointent dans la direction de \(y\)l'axe positif, notre pouce pointe dans la direction de l'\(z\)axe positif (Figure\(\PageIndex{1b}\)). Dans ce texte, nous travaillons toujours avec des systèmes de coordonnées définis conformément à la règle de la main droite. Certains systèmes suivent une règle de la main gauche, mais la règle de la main droite est considérée comme la représentation standard.
En deux dimensions, nous décrivons un point du plan avec ses coordonnées\((x,y)\). Chaque coordonnée décrit la façon dont le point s'aligne sur l'axe correspondant. En trois dimensions, une nouvelle coordonnée,\(z\), est ajoutée pour indiquer l'alignement avec l'\(z\)axe :\((x,y,z)\). Un point dans l'espace est identifié par les trois coordonnées (Figure\(\PageIndex{2}\)). Pour tracer le point\((x,y,z)\), repérez les\(x\) unités le long de \(x\)l'axe -, puis les \(y\)unités dans la direction de\(y\) l'axe -, puis les\(z\) unités dans la direction de l'\(z\)axe.
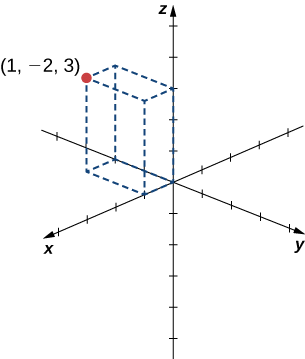
Esquissez le point\((1,−2,3)\) dans un espace tridimensionnel.
Solution
Pour esquisser un point, commencez par dessiner trois côtés d'un prisme rectangulaire le long des axes de coordonnées : une unité dans la\(x\) direction positive, des\(2\) unités dans la\(y\) direction négative et des\(3\) unités dans la\(z\) direction positive. Complétez le prisme pour tracer le point (Figure\(\PageIndex{3}\)).
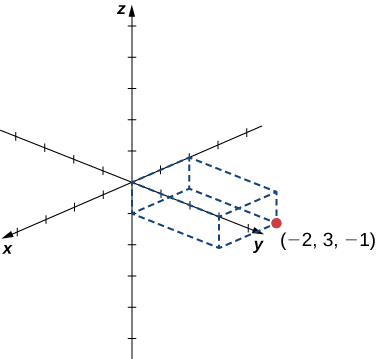
Esquissez le point\((−2,3,−1)\) dans un espace tridimensionnel.
- Allusion
-
Commencez par esquisser les axes de coordonnées. Par exemple, Figure\(\PageIndex{3}\). Esquissez ensuite un prisme rectangulaire pour vous aider à trouver le point dans l'espace.
- Réponse
-
Dans un espace bidimensionnel, le plan de coordonnées est défini par une paire d'axes perpendiculaires. Ces axes nous permettent de nommer n'importe quel emplacement dans le plan. En trois dimensions, nous définissons des plans de coordonnées par les axes de coordonnées, tout comme en deux dimensions. Il y a maintenant trois axes, donc il y a trois paires d'axes qui se croisent. Chaque paire d'axes forme un plan de coordonnées : le\(xy\) plan, le \(xz\)plan et le\(yz\) plan (Figure\(\PageIndex{4}\)). Nous définissons formellement le\(xy\) -plane comme l'ensemble suivant :\(\{(x,y,0):x,y∈ℝ\}.\) De même, le \(xz\)-plane et le\(yz\) -plane sont définis\(\{(0,y,z):y,z∈ℝ\},\) respectivement comme\(\{(x,0,z):x,z∈ℝ\}\) et.
Pour visualiser cela, imaginez que vous construisez une maison et que vous vous trouvez dans une pièce dont seuls deux des quatre murs sont terminés. (Supposons que les deux murs finis soient adjacents.) Si vous vous tenez dos au coin où les deux murs finis se rejoignent, face à la pièce, le sol est le\(xy\) plan, le mur à votre droite est le \(xz\)plan et le mur à gauche est le \(yz\)plan.
En deux dimensions, les axes de coordonnées divisent le plan en quatre quadrants. De même, les plans de coordonnées divisent l'espace entre eux en huit régions autour de l'origine, appelées octants. Les octants se remplissent\(ℝ^3\) de la même manière que les quadrants\(ℝ^2\), comme le montre la figure\(\PageIndex{5}\).
La plupart des travaux dans un espace tridimensionnel constituent une extension confortable des concepts correspondants en deux dimensions. Dans cette section, nous utilisons notre connaissance des cercles pour décrire des sphères, puis nous étendons notre compréhension des vecteurs à trois dimensions. Pour atteindre ces objectifs, nous commençons par adapter la formule de distance à l'espace tridimensionnel.
Si deux points se trouvent dans le même plan de coordonnées, il est facile de calculer la distance qui les sépare. Nous savons que la distance\(d\) entre deux points\((x_1,y_1)\) et\((x_2,y_2)\) dans le plan de\(xy\) coordonnées est donnée par la formule
\[d=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2}. \nonumber \]
La formule de la distance entre deux points de l'espace est une extension naturelle de cette formule.
La distance\(d\) entre les points\((x_1,y_1,z_1)\) et\((x_2,y_2,z_2)\) est donnée par la formule
\[d=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2+(z_2−z_1)^2}. \label{distanceForm} \]
La preuve de ce théorème est présentée à titre d'exercice. (Conseil : trouvez d'abord la distance\(d_1\) entre\((x_1,y_1,z_1)\) les points,\((x_2,y_2,z_1)\) comme indiqué sur la figure\(\PageIndex{6}\).)
Trouvez la distance entre les points\(P_1=(3,−1,5)\) et\(P_2=(2,1,−1).\)
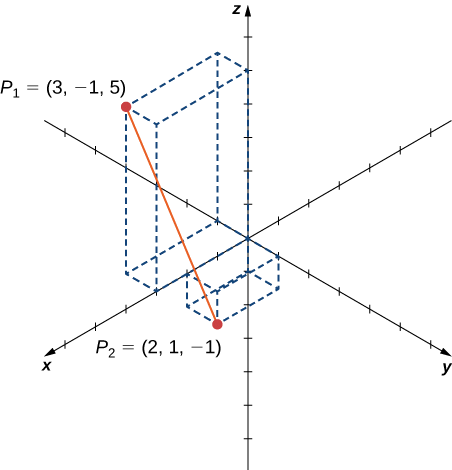
Solution
Substituez les valeurs directement dans la formule de distance (Equation \ ref {DistanceForm}) :
\[\begin{align*} d(P_1,P_2) &=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2+(z_2−z_1)^2} \\[4pt] &=\sqrt{(2−3)^2+(1−(−1))^2+(−1−5)^2} \\[4pt] &=\sqrt{(-1)^2+2^2+(−6)^2} \\[4pt] &=\sqrt{41}. \end{align*}\]
Trouvez la distance entre les points\(P_1=(1,−5,4)\) et\(P_2=(4,−1,−1)\).
- Allusion
-
\(d=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2+(z_2−z_1)^2}\)
- Réponse
-
\(5\sqrt{2}\)
Avant de passer à la section suivante, voyons en quoi cela\(ℝ^3\) diffère de\(ℝ^2\). Par exemple, dans\(ℝ^2\), les lignes qui ne sont pas parallèles doivent toujours se croiser. Ce n'est pas le cas dans\(ℝ^3\). Par exemple, considérez les lignes illustrées dans la figure\(\PageIndex{8}\). Ces deux lignes ne sont pas parallèles et ne se croisent pas.
Figure\(\PageIndex{8}\) : Ces deux lignes ne sont pas parallèles, mais elles ne se croisent pas.
Vous pouvez également avoir des cercles interconnectés mais n'ayant aucun point commun, comme dans la Figure\(\PageIndex{9}\).
Figure\(\PageIndex{9}\) : Ces cercles sont interconnectés, mais n'ont aucun point commun.
Nous avons beaucoup plus de flexibilité en travaillant en trois dimensions que si nous nous en tenions à deux dimensions seulement.
Écrire des équations dans\(ℝ^3\)
Maintenant que nous pouvons représenter des points dans l'espace et trouver la distance qui les sépare, nous pouvons apprendre à y écrire des équations d'objets géométriques tels que des lignes, des plans et des surfaces courbes\(ℝ^3\). Tout d'abord, nous commençons par une équation simple. Comparez les graphiques de l'équation\(x=0\) dans\(ℝ\)\(ℝ^2\), et\(ℝ^3\) (Figure\(\PageIndex{10}\)). À partir de ces graphiques, nous pouvons voir que la même équation peut décrire un point, une ligne ou un plan.
Dans l'espace, l'équation\(x=0\) décrit tous les points\((0,y,z)\). Cette équation définit le\(yz\) plan. De même, le\(xy\) plan contient tous les points du formulaire\((x,y,0)\). L'équation\(z=0\) définit le \(xy\)plan -et l'équation\(y=0\) décrit le\(xz\) plan -plan (Figure\(\PageIndex{11}\)).
La compréhension des équations des plans de coordonnées nous permet d'écrire une équation pour n'importe quel plan parallèle à l'un des plans de coordonnées. Lorsqu'un plan est parallèle au \(xy\)plan, par exemple, la coordonnée\(z\) - de chaque point du plan a la même valeur constante. Seules les coordonnées\(x\) - et \(y\)- des points de ce plan varient d'un point à l'autre.
- Le plan de l'espace qui est parallèle au\(xy\) plan -et qui contient le point\((a,b,c)\) peut être représenté par l'équation\(z=c\).
- Le plan de l'espace qui est parallèle au\(xz\) plan -et qui contient le point\((a,b,c)\) peut être représenté par l'équation\(y=b\).
- Le plan de l'espace qui est parallèle au\(yz\) plan -et qui contient le point\((a,b,c)\) peut être représenté par l'équation\(x=a\).
- Ecrivez une équation du plan passant par un point\((3,11,7)\) parallèle au\(yz\) plan.
- Trouvez une équation du plan passant par des points\((6,−2,9), (0,−2,4),\) et\((1,−2,−3).\)
Solution
- Lorsqu'un plan est parallèle au\(yz\) plan, seules les\(z\) coordonnées \(y\)- et - peuvent varier. La\(x\) coordonnée -a la même valeur constante pour tous les points de ce plan, ce plan peut donc être représenté par l'équation\(x=3\).
- Chacun\((6,−2,9), (0,−2,4),\) des points\((1,−2,−3)\) a la même\(y\) coordonnée. Ce plan peut être représenté par l'équation\(y=−2\).
Ecrivez une équation du plan passant par un point\((1,−6,−4)\) parallèle au\(xy\) plan.
- Allusion
-
Si un plan est parallèle au\(xy\) plan, les coordonnées z des points de ce plan ne varient pas.
- Réponse
-
\(z=−4\)
Comme nous l'avons vu,\(ℝ^2\) l'équation\(x=5\) décrit la ligne verticale passant par le point\((5,0)\). Cette ligne est parallèle à l'\(y\)axe. Dans une extension naturelle, l'équation\(x=5\) de\(ℝ^3\) décrit le plan passant par le point\((5,0,0)\), qui est parallèle au \(yz\)plan. Une autre extension naturelle d'une équation familière se trouve dans l'équation d'une sphère.
Une sphère est l'ensemble de tous les points de l'espace équidistants d'un point fixe, le centre de la sphère (Figure\(\PageIndex{12}\)), tout comme l'ensemble de tous les points d'un plan équidistants du centre représente un cercle. Dans une sphère, comme dans un cercle, la distance entre le centre et un point de la sphère est appelée rayon.
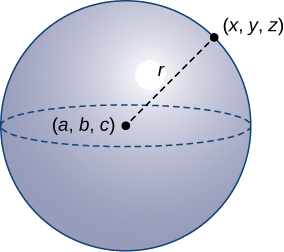
L'équation d'un cercle est dérivée à l'aide de la formule de distance en deux dimensions. De la même manière, l'équation d'une sphère est basée sur la formule tridimensionnelle de la distance.
La sphère avec centre\((a,b,c)\) et rayon\(r\) peut être représentée par l'équation
\[(x−a)^2+(y−b)^2+(z−c)^2=r^2. \nonumber \]
Cette équation est connue sous le nom d'équation standard d'une sphère.
Trouvez l'équation standard de la sphère avec le centre\((10,7,4)\) et le point\((−1,3,−2)\), comme indiqué sur la figure\(\PageIndex{13}\).
Figure\(\PageIndex{13}\) : La sphère centrée sur le point de\((10,7,4)\) confinement\((−1,3,−2).\)
Solution
Utilisez la formule de distance pour déterminer le rayon\(r\) de la sphère :
\[\begin{align*} r &=\sqrt{(−1−10)^2+(3−7)^2+(−2−4)^2} \\[4pt] &=\sqrt{(−11)^2+(−4)^2+(−6)^2} \\[4pt] &=\sqrt{173} \end{align*} \nonumber \]
L'équation standard de la sphère est
\[(x−10)^2+(y−7)^2+(z−4)^2=173. \nonumber \]
Trouvez l'équation standard de la sphère dont le centre\((−2,4,−5)\) contient le point\((4,4,−1).\)
- Allusion
-
Utilisez d'abord la formule de distance pour déterminer le rayon de la sphère.
- Réponse
-
\[(x+2)^2+(y−4)^2+(z+5)^2=52 \nonumber \]
Supposons que le segment de ligne\(\overline{PQ}\) forme le diamètre d'une sphère (Figure\(\PageIndex{14}\)).\(P=(−5,2,3)\)\(Q=(3,4,−1)\) Trouvez l'équation de la sphère.
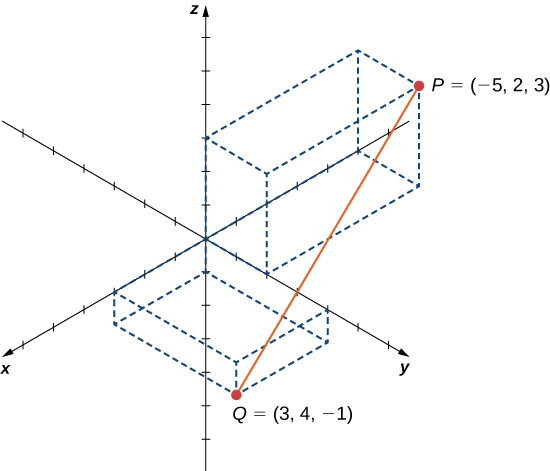
Solution :
Comme\(\overline{PQ}\) c'est le diamètre de la sphère, nous savons que le centre de la sphère est le point médian de\(\overline{PQ}\) .Ensuite,
\[C=\left(\dfrac{−5+3}{2},\dfrac{2+4}{2},\dfrac{3+(−1)}{2}\right)=(−1,3,1). \nonumber \]
De plus, nous savons que le rayon de la sphère est égal à la moitié de la longueur du diamètre. Cela donne
\[\begin{align*} r &=\dfrac{1}{2}\sqrt{(−5−3)^2+(2−4)^2+(3−(−1))^2} \\[4pt] &=\dfrac{1}{2}\sqrt{64+4+16} \\[4pt] &=\sqrt{21} \end{align*}\]
Ensuite, l'équation de la sphère est\((x+1)^2+(y−3)^2+(z−1)^2=21.\)
Trouvez l'équation de la sphère avec le diamètre\(\overline{PQ}\), où\(P=(2,−1,−3)\) et\(Q=(−2,5,−1).\)
- Allusion
-
Déterminez d'abord le point médian du diamètre.
- Réponse
-
\[x^2+(y−2)^2+(z+2)^2=14 \nonumber \]
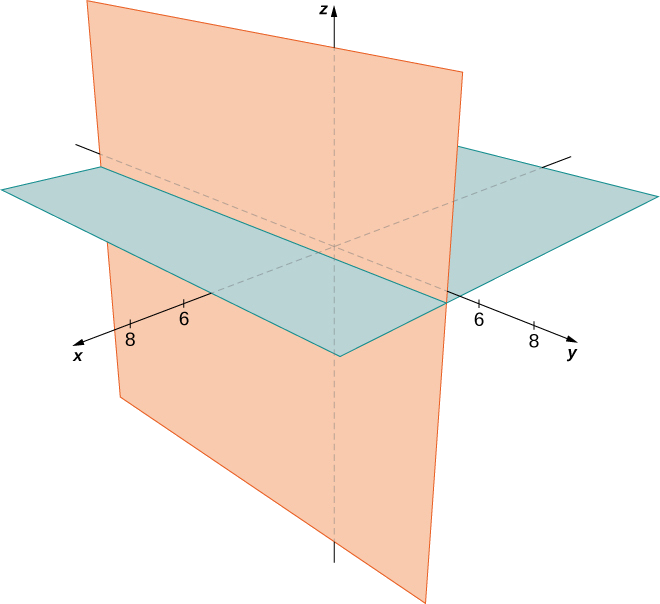
Décrivez l'ensemble de points qui satisfait\((x−4)(z−2)=0,\) et représentez l'ensemble sous forme graphique.
Solution
Nous devons avoir l'un\(x−4=0\) ou l'autre\(z−2=0\), donc l'ensemble des points forme les deux plans\(x=4\) et\(z=2\) (Figure\(\PageIndex{15}\)).
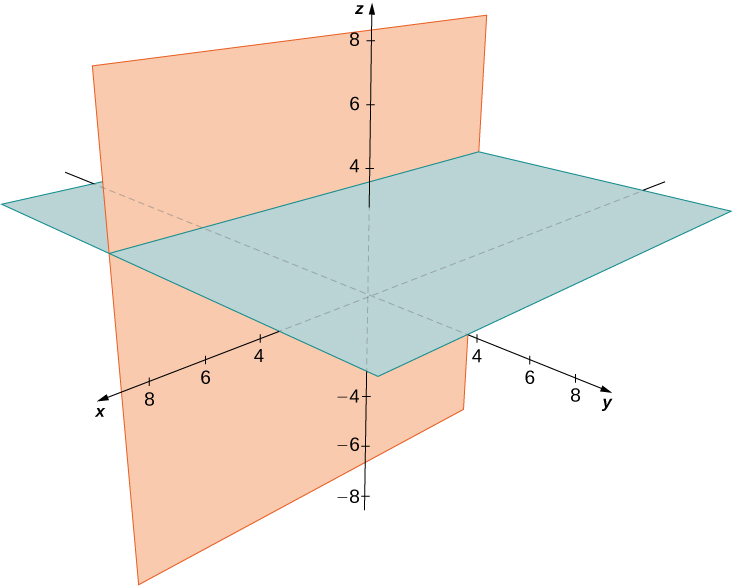
Décrivez l'ensemble de points qui satisfait\((y+2)(z−3)=0,\) et représentez l'ensemble sous forme graphique.
- Allusion
-
L'un des facteurs doit être zéro.
- Réponse
-
L'ensemble de points forme les deux plans\(y=−2\) et\(z=3\).
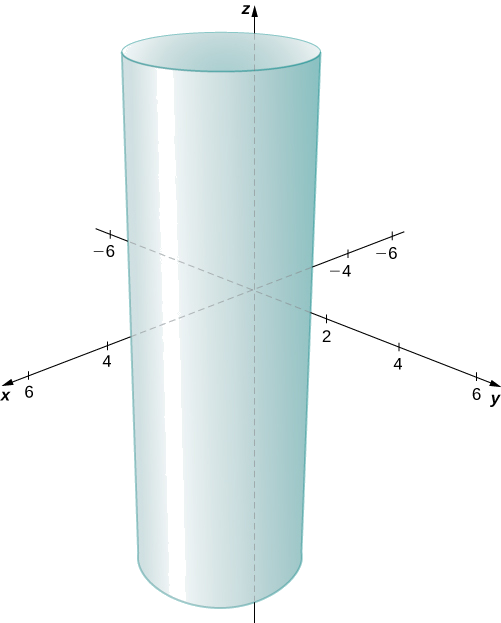
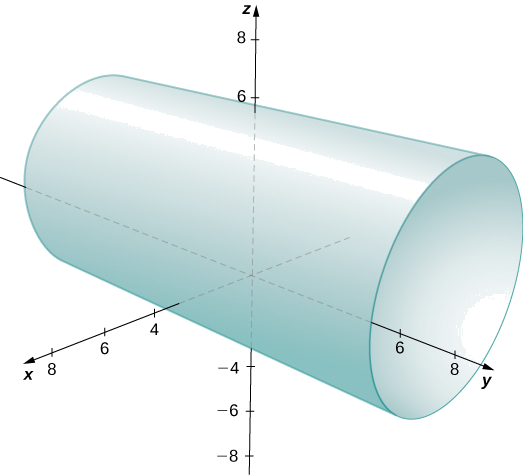
Décrivez l'ensemble de points dans un espace tridimensionnel qui satisfait\((x−2)^2+(y−1)^2=4,\) et représentez l'ensemble sous forme graphique.
Solution
Les \(y\)coordonnées\(x\) - et - forment un cercle dans le \(xy\)plan du rayon\(2\), centré sur\((2,1)\). Comme il n'y a aucune restriction sur la \(z\)coordonnée, le résultat tridimensionnel est un cylindre circulaire de rayon\(2\) centré sur la ligne avec\(x=2\) et\(y=1\). Le cylindre s'étend indéfiniment dans la\(z\) direction (Figure\(\PageIndex{16}\)).
Décrivez l'ensemble de points dans un espace tridimensionnel qui satisfait\(x^2+(z−2)^2=16\) et tracez la surface.
- Allusion
-
Réfléchissez à ce qui se passe si vous tracez cette équation en deux dimensions dans le\(xz\) plan.
- Réponse
-
Un cylindre de rayon 4 centré sur la ligne avec\(x=0\) et\(z=2\).
Utilisation de vecteurs dans\(ℝ^3\)
Tout comme les vecteurs bidimensionnels, les vecteurs tridimensionnels sont des quantités ayant à la fois une amplitude et une direction, et ils sont représentés par des segments de ligne dirigés (flèches). Avec un vecteur tridimensionnel, nous utilisons une flèche tridimensionnelle.
Les vecteurs tridimensionnels peuvent également être représentés sous forme de composants. La notation\(\vecs{v}=⟨x,y,z⟩\) est une extension naturelle du cas bidimensionnel, représentant un vecteur avec le point initial à l'origine et le point terminal\((x,y,z)\).\((0,0,0)\) Le vecteur zéro est\(\vecs{0}=⟨0,0,0⟩\). Ainsi, par exemple, le vecteur tridimensionnel\(\vecs{v}=⟨2,4,1⟩\) est représenté par un segment de ligne dirigé d'un point\((0,0,0)\) à l'autre\((2,4,1)\) (Figure\(\PageIndex{17}\)).
L'addition de vecteurs et la multiplication scalaire sont définies de manière analogue au cas bidimensionnel. Si\(\vecs{v}=⟨x_1,y_1,z_1⟩\) et\(\vecs{w}=⟨x_2,y_2,z_2⟩\) sont des vecteurs, et\(k\) est un scalaire, alors
\[\vecs{v}+\vecs{w}=⟨x_1+x_2,y_1+y_2,z_1+z_2⟩ \nonumber \]
et
\[k\vecs{v}=⟨kx_1,ky_1,kz_1⟩. \nonumber \]
Si\(k=−1,\) alors\(k\vecs{v}=(−1)\vecs{v}\) est écrit comme\(−\vecs{v}\), et la soustraction vectorielle est définie par\(\vecs{v}−\vecs{w}=\vecs{v}+(−\vecs{w})=\vecs{v}+(−1)\vecs{w}\).
Les vecteurs unitaires standard s'étendent également facilement en trois dimensions,\(\hat{\mathbf i}=⟨1,0,0⟩\), et\(\hat{\mathbf j}=⟨0,1,0⟩\)\(\hat{\mathbf k}=⟨0,0,1⟩\), et nous les utilisons de la même manière que nous avons utilisé les vecteurs unitaires standard en deux dimensions. Ainsi, nous pouvons représenter un vecteur de la\(ℝ^3\) manière suivante :
\[\vecs{v}=⟨x,y,z⟩=x\hat{\mathbf i}+y\hat{\mathbf j}+z\hat{\mathbf k} \nonumber \].
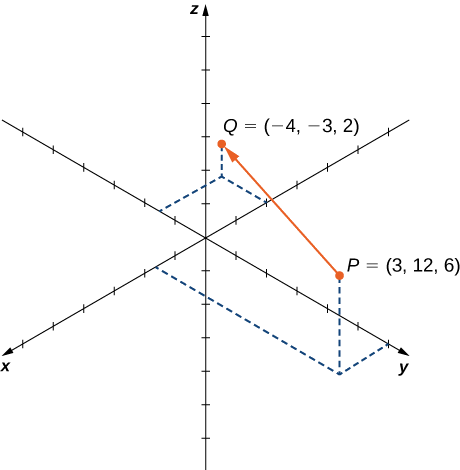
\(\vecd{PQ}\)Soit le vecteur avec le point initial\(P=(3,12,6)\) et le point terminal,\(Q=(−4,−3,2)\) comme indiqué sur la figure\(\PageIndex{18}\). Exprimez\(\vecd{PQ}\) à la fois sous forme de composants et en utilisant des vecteurs unitaires standard
Solution
Sous forme de composant,
\[\begin{align*} \vecd{PQ} =⟨x_2−x_1,y_2−y_1,z_2−z_1⟩ \\[4pt] =⟨−4−3,−3−12,2−6⟩ \\[4pt] =⟨−7,−15,−4⟩. \end{align*}\]
Sous forme unitaire standard,
\[\vecd{PQ}=−7\hat{\mathbf i}−15\hat{\mathbf j}−4\hat{\mathbf k}. \nonumber \]
Laissez\(S=(3,8,2)\) et\(T=(2,−1,3)\). \(\vec{ST}\)Exprime sous forme de composant et sous forme d'unité standard.
- Allusion
-
Écrivez\(\vecd{ST}\) d'abord sous forme de composant. \(T\)est le point terminal de\(\vecd{ST}\).
- Réponse
-
\(\vecd{ST}=⟨−1,−9,1⟩=−\hat{\mathbf i}−9\hat{\mathbf j}+\hat{\mathbf k}\)
Comme décrit précédemment, les vecteurs en trois dimensions se comportent de la même manière que les vecteurs dans un plan. L'interprétation géométrique de l'addition de vecteurs, par exemple, est la même dans l'espace bidimensionnel et tridimensionnel (Figure\(\PageIndex{19}\)).
Nous avons déjà vu comment certaines propriétés algébriques des vecteurs, telles que l'addition de vecteurs et la multiplication scalaire, peuvent être étendues en trois dimensions. D'autres propriétés peuvent être étendues de la même manière. Ils sont résumés ici à titre de référence.
Laissons\(\vecs{v}=⟨x_1,y_1,z_1⟩\) et\(\vecs{w}=⟨x_2,y_2,z_2⟩\) soyez des vecteurs, et\(k\) soyez un scalaire.
- Multiplication scalaire :\[k\vecs{v}=⟨kx_1,ky_1,kz_1⟩ \nonumber \]
- Ajout de vecteurs :\[\vecs{v}+\vecs{w}=⟨x_1,y_1,z_1⟩+⟨x_2,y_2,z_2⟩=⟨x_1+x_2,y_1+y_2,z_1+z_2⟩ \nonumber \]
- Soustraction vectorielle :\[\vecs{v}−\vecs{w}=⟨x_1,y_1,z_1⟩−⟨x_2,y_2,z_2⟩=⟨x_1−x_2,y_1−y_2,z_1−z_2⟩ \nonumber \]
- Grandeur du vecteur :\[\|\vecs{v}\|=\sqrt{x_1^2+y_1^2+z_1^2} \nonumber \]
- Vecteur unitaire dans la direction de\(\vecs{v}\) :\[\dfrac{1}{\|\vecs{v}\|}\vecs{v}=\dfrac{1}{\|\vecs{v}\|}⟨x_1,y_1,z_1⟩=⟨\dfrac{x_1}{\|\vecs{v}\|},\dfrac{y_1}{\|\vecs{v}\|},\dfrac{z_1}{\|\vecs{v}\|}⟩, \quad \text{if} \, \vecs{v}≠\vecs{0} \nonumber \]
Nous avons vu que l'addition de vecteurs en deux dimensions satisfait les propriétés inverses commutatives, associatives et additives. Ces propriétés des opérations vectorielles sont également valables pour les vecteurs tridimensionnels. La multiplication scalaire des vecteurs satisfait à la propriété distributive, et le vecteur zéro agit comme une identité additive. Les preuves permettant de vérifier ces propriétés en trois dimensions sont de simples extensions des preuves en deux dimensions.
Laissons\(\vecs{v}=⟨−2,9,5⟩\) et\(\vecs{w}=⟨1,−1,0⟩\) (Figure\(\PageIndex{20}\)). Trouvez les vecteurs suivants.
- \(3\vecs{v}−2\vecs{w}\)
- \(5\|\vecs{w}\|\)
- \(\|5 \vecs{w}\|\)
- Un vecteur unitaire dans la direction de\(\vecs{v}\)
Solution
a. D'abord, utilisez la multiplication scalaire de chaque vecteur, puis soustrayez :
\[\begin{align*} 3\vecs{v}−2\vecs{w} =3⟨−2,9,5⟩−2⟨1,−1,0⟩ \\[4pt] =⟨−6,27,15⟩−⟨2,−2,0⟩ \\[4pt] =⟨−6−2,27−(−2),15−0⟩ \\[4pt] =⟨−8,29,15⟩. \end{align*}\]
b. Écrivez l'équation de la magnitude du vecteur, puis utilisez la multiplication scalaire :
\[5\|\vecs{w}\|=5\sqrt{1^2+(−1)^2+0^2}=5\sqrt{2}. \nonumber \]
c. Utilisez d'abord la multiplication scalaire, puis déterminez l'amplitude du nouveau vecteur. Notez que le résultat est le même que pour la partie b. :
\[\|5 \vecs{w}\|=∥⟨5,−5,0⟩∥=\sqrt{5^2+(−5)^2+0^2}=\sqrt{50}=5\sqrt{2} \nonumber \]
d. Rappelons que pour trouver un vecteur unitaire en deux dimensions, on divise un vecteur par sa magnitude. La procédure est la même en trois dimensions :
\[\begin{align*} \dfrac{\vecs{v}}{\|\vecs{v}\|} =\dfrac{1}{\|\vecs{v}\|}⟨−2,9,5⟩ \\[4pt] =\dfrac{1}{\sqrt{(−2)^2+9^2+5^2}}⟨−2,9,5⟩ \\[4pt] =\dfrac{1}{\sqrt{110}}⟨−2,9,5⟩ \\[4pt] =⟨\dfrac{−2}{\sqrt{110}},\dfrac{9}{\sqrt{110}},\dfrac{5}{\sqrt{110}}⟩ . \end{align*}\]
Laissez\(\vecs{v}=⟨−1,−1,1⟩\) et\(\vecs{w}=⟨2,0,1⟩\). Trouvez un vecteur unitaire dans la direction de\(5\vecs{v}+3\vecs{w}.\)
- Allusion
-
Commencez par écrire\(5\vecs{v}+3\vecs{w}\) sous forme de composant.
- Réponse
-
\(⟨\dfrac{1}{3\sqrt{10}},−\dfrac{5}{3\sqrt{10}},\dfrac{8}{3\sqrt{10}}⟩\)
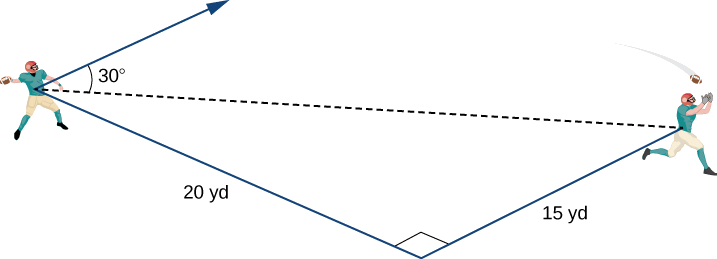
Un quarterback se tient debout sur le terrain de football et s'apprête à lancer une passe. Son receveur se tient à 20 mètres sur le terrain et à 15 mètres de la gauche du quarterback. Le quarterback lance le ballon à une vitesse de 60 mi/h vers le receveur avec un angle ascendant de\(30°\) (voir la figure suivante). Ecrivez le vecteur de vitesse initial de la balle\(\vecs{v}\), sous forme de composant.
Solution
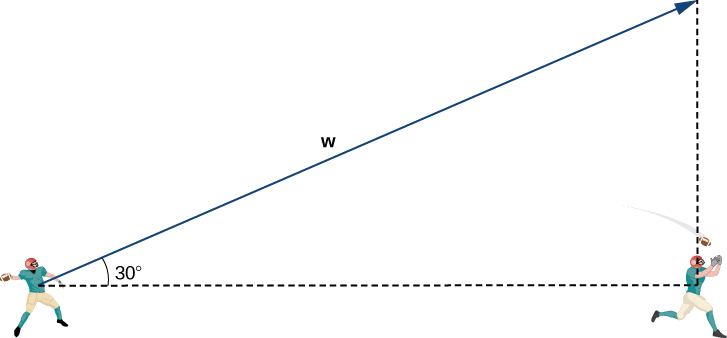
La première chose que nous voulons faire est de trouver un vecteur dans la même direction que le vecteur de vitesse de la balle. Nous redimensionnons ensuite le vecteur de manière appropriée afin qu'il ait la bonne magnitude. Considérez le vecteur\(\vecs{w}\) s'étendant du bras du quarterback à un point situé directement au-dessus de la tête du receveur selon un angle de\(30°\) (voir la figure suivante). Ce vecteur aurait la même direction que\(\vecs{v}\), mais il se peut qu'il n'ait pas la bonne amplitude.
Le receveur se trouve à 20 mètres du terrain et à 15 mètres de la gauche du quarterback. Par conséquent, la distance en ligne droite entre le quarterback et le receveur est
Dist de QB au récepteur\(=\sqrt{15^2+20^2}=\sqrt{225+400}=\sqrt{625}=25\) yd.
Nous avons\(\dfrac{25}{\|\vecs{w}\|}=\cos 30°.\) Alors la magnitude de\(\vecs{w}\) est donnée par
\(\|\vecs{w}\|=\dfrac{25}{\cos 30°}=\dfrac{25⋅2}{\sqrt{3}}=\dfrac{50}{\sqrt{3}}\)yd
et la distance verticale entre le récepteur et le point terminal de\(\vecs{w}\) est
Verse la distance entre le récepteur et le point terminal de\(\vecs{w}=\|\vecs{w}\| \sin 30°=\dfrac{50}{\sqrt{3}}⋅\dfrac{1}{2}=\dfrac{25}{\sqrt{3}}\) yd.
Ensuite\(\vecs{w}=⟨20,15,\dfrac{25}{\sqrt{3}}⟩\), et a la même direction que\(\vecs{v}\).
Rappelez-vous, cependant, que nous avons calculé la magnitude de\(\vecs{w}\) à\(\|\vecs{w}\|=\dfrac{50}{\sqrt{3}}\) yd et que nous avons\(\vecs{v}\) une magnitude\(60\) mph. Nous devons donc multiplier le vecteur\(\vecs{w}\) par une constante appropriée,\(k\). Nous voulons trouver une valeur de\(k\) telle que\(∥k\vecs{w}∥=60\) mph *. Nous avons
\(\|k \vecs{w}\|=k\|\vecs{w}\|=k\dfrac{50}{\sqrt{3}}\)1 jour,
donc nous voulons
\(k \left(\dfrac{50}{\sqrt{3}}\text{ yd}\right) =60\)mi/h
\(k=\dfrac{60\sqrt{3}}{50}\)mi/h/an
\(k=\dfrac{6\sqrt{3}}{5}\)mi/h/yd.
Alors
\(\vecs{v}=k\vecs{w}=k⟨20,15,\dfrac{25}{\sqrt{3}}⟩=\dfrac{6\sqrt{3}}{5}\;⟨20,15,\dfrac{25}{\sqrt{3}}⟩=⟨24\sqrt{3},18\sqrt{3},30⟩\).
Vérifions-le à nouveau ce\(\|\vecs{v}\|=60\) mph. Nous avons
\(\|\vecs{v}\|=\sqrt{(24\sqrt{3})^2+(18\sqrt{3})^2+(30)^2}=\sqrt{1728+972+900}=\sqrt{3600}=60\)mi/h.
Nous avons donc trouvé les bons composants pour\(\vecs{v}\).
Les lecteurs qui ont étudié les unités de mesure se demandent peut-être ce qui se passe exactement à ce stade : n'avons-nous pas simplement mélangé mètres et miles par heure ? Nous ne l'avons pas fait, mais la raison est subtile. Une façon de le comprendre est de se rendre compte qu'il existe réellement deux systèmes de coordonnées parallèles dans ce problème : l'un donne les positions sur le terrain, à travers le champ et dans les airs en unités de mètres ; l'autre donne les vitesses sur le terrain, à travers le champ et dans les airs en unités de miles par heure. Le vecteur\(\vecs{w}\) est calculé dans le système de coordonnées de position ; le vecteur\(\vecs{v}\) sera dans le système de vitesse. Comme les axes correspondants dans chaque système sont parallèles, les directions des deux systèmes sont également parallèles, de sorte que l'affirmation selon laquelle\(\vecs{w}\) et\(\vecs{v}\) pointent dans la même direction est correcte. La constante\(k\) que nous recherchons est un facteur de conversion entre les magnitudes de ces deux vecteurs, passant du système de position au système de vitesse. Et comme nous l'avons vu plus haut, notre calcul de\(k\) produit les bonnes unités pour une telle conversion, à savoir les miles par heure et par mètre.
Supposons que le quarterback et le receveur se trouvent au même endroit que dans l'exemple précédent. Cette fois, cependant, le quarterback lance le ballon à une vitesse de\(40\) mph et à un angle de\(45°\). Ecrivez le vecteur de vitesse initial de la balle\(\vecs{v}\), sous forme de composant.
- Allusion
-
Suivez le processus utilisé dans l'exemple précédent.
- Réponse
-
\(v=⟨16\sqrt{2},12\sqrt{2},20\sqrt{2}⟩\)
Concepts clés
- Le système de coordonnées tridimensionnel est construit autour d'un ensemble de trois axes qui se croisent à angle droit en un point unique, l'origine. Les triples\((x,y,z)\) ordonnés sont utilisés pour décrire l'emplacement d'un point dans l'espace.
- La distance\(d\) entre les points\((x_1,y_1,z_1)\) et\((x_2,y_2,z_2)\) est donnée par la formule\[d=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2+(z_2−z_1)^2}.\nonumber \]
- En trois dimensions, les équations\(x=a,\, y=b,\) et\(z=c\) décrivent des plans parallèles aux plans de coordonnées.
- L'équation standard d'une sphère avec centre\((a,b,c)\) et rayon\(r\) est\[(x−a)^2+(y−b)^2+(z−c)^2=r^2. \nonumber \]
- En trois dimensions, comme en deux, les vecteurs sont généralement exprimés sous forme de composants\(\vecs v=⟨x,y,z⟩\), ou en termes de vecteurs unitaires standard,\(\vecs v= x\,\mathbf{\hat i}+y\,\mathbf{\hat j}+z\,\mathbf{\hat k}.\)
- Les propriétés des vecteurs dans l'espace sont une extension naturelle des propriétés des vecteurs dans un plan. Laissons\(\vecs v=⟨x_1,y_1,z_1⟩\) et\(\vecs w=⟨x_2,y_2,z_2⟩\) soyez des vecteurs, et\(k\) soyez un scalaire.
Multiplication scalaire :
\[k\vecs{v}=⟨kx_1,ky_1,kz_1⟩ \nonumber \]
Ajout de vecteurs :
\[\vecs{v}+\vecs{w}=⟨x_1,y_1,z_1⟩+⟨x_2,y_2,z_2⟩=⟨x_1+x_2,y_1+y_2,z_1+z_2⟩ \nonumber \]
Soustraction vectorielle :
\[\vecs{v}−\vecs{w}=⟨x_1,y_1,z_1⟩−⟨x_2,y_2,z_2⟩=⟨x_1−x_2,y_1−y_2,z_1−z_2⟩ \nonumber \]
Grandeur du vecteur :
\[‖\vecs{v}‖=\sqrt{x_1^2+y_1^2+z_1^2} \nonumber \]
Vecteur unitaire dans la direction de\(\vecs{v}\) :
\[\dfrac{\vecs{v}}{‖\vecs{v}‖}=\dfrac{1}{‖\vecs{v}‖}⟨x_1,y_1,z_1⟩=⟨\dfrac{x_1}{‖\vecs{v}‖},\dfrac{y_1}{‖\vecs{v}‖},\dfrac{z_1}{‖\vecs{v}‖}⟩, \; \vecs{v}≠\vecs{0} \nonumber \]
Équations clés
Distance entre deux points de l'espace :
\[d=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2+(z_2−z_1)^2} \nonumber \]
Sphère avec centre\((a,b,c)\) et rayon\(r\) :
\[(x−a)^2+(y−b)^2+(z−c)^2=r^2 \nonumber \]
Lexique
- plan de coordonnées
- un plan contenant deux des trois axes de coordonnées du système de coordonnées tridimensionnel, nommés selon les axes qu'il contient : le\(xy\)\(xz\) plan, le plan ou le\(yz\) plan
- règle de la main droite
- une méthode courante pour définir l'orientation du système de coordonnées tridimensionnel ; lorsque la main droite est courbée autour de\(z\) l'axe -de telle sorte que les doigts s'enroulent de l'\(x\)axe positif à l'\(y\)axe positif, le pouce pointe dans la direction de l'\(z\)axe positif
- octants
- les huit régions de l'espace créées par les plans de coordonnées
- sphère
- l'ensemble de tous les points équidistants d'un point donné appelé le centre
- équation standard d'une sphère
- \((x−a)^2+(y−b)^2+(z−c)^2=r^2\)décrit une sphère avec un centre\((a,b,c)\) et un rayon\(r\)
- système de coordonnées rectangulaires tridimensionnelles
- un système de coordonnées défini par trois lignes qui se croisent à angle droit ; chaque point de l'espace est décrit par un triple ordonné\((x,y,z)\) qui trace sa position par rapport aux axes de définition
Contributeurs
\(\PageIndex{10}\)L'exemple a été modifié par Doug Baldwin et Paul Seeburger afin de clarifier les unités de mesure utilisées et la manière dont il les utilise.
Paul Seeburger a également créé des versions dynamiques de\(\PageIndex{8}, \PageIndex{9}\) Figures\(\PageIndex{13}\) en utilisant CalcPlot3D.


