7.8 : Chapitre 7 : Exercices de révision

Last updated
Save as PDF

Page ID: 197624

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Dans les exercices 1 à 4, déterminez si l'énoncé est vrai ou faux. Justifiez votre réponse par une preuve ou un contre-exemple.

1)$\displaystyle ∫e^x\sin(x)\,dx$ ne peut pas être intégré par pièces.

2)$\displaystyle ∫\frac{1}{x^4+1}\,dx$ ne peut pas être intégré en utilisant des fractions partielles.

Réponse: Faux

3) Dans l'intégration numérique, l'augmentation du nombre de points diminue l'erreur.

4) L'intégration par pièces peut toujours donner l'intégrale.

Réponse: Faux

Dans les exercices 5 à 10, évaluez l'intégrale en utilisant la méthode spécifiée.

5)$\displaystyle ∫x^2\sin(4x)\,dx,$ utilisation de l'intégration par pièces

6)$\displaystyle ∫\frac{1}{x^2\sqrt{x^2+16}}\,dx,$ en utilisant la substitution trigonométrique

Réponse: $\displaystyle ∫\frac{1}{x^2\sqrt{x^2+16}}\,dx = −\frac{\sqrt{x^2+16}}{16x}+C$

7)$\displaystyle ∫\sqrt{x}\ln x\,dx,$ en utilisant l'intégration par pièces

8)$\displaystyle ∫\frac{3x}{x^3+2x^2−5x−6}\,dx,$ en utilisant des fractions partielles

Réponse: $\displaystyle ∫\frac{3x}{x^3+2x^2−5x−6}\,dx = \frac{1}{10}\big(4\ln|2−x|+5\ln|x+1|−9\ln|x+3|\big)+C$

9)$\displaystyle ∫\frac{x^5}{(4x^2+4)^{5/2}}\,dx,$ en utilisant la substitution trigonométrique

10)$\displaystyle ∫\frac{\sqrt{4−\sin^2(x)}}{\sin^2(x)}\cos(x)\,dx,$ à l'aide d'une table d'intégrales ou d'un CAS

Réponse: $\displaystyle ∫\frac{\sqrt{4−\sin^2(x)}}{\sin^2(x)}\cos(x)\,dx = −\frac{\sqrt{4−\sin^2(x)}}{\sin(x)}−\frac{x}{2}+C$

Dans les exercices 11 à 15, intégrez en utilisant la méthode de votre choix.

11)$\displaystyle ∫\sin^2 x\cos^2 x\,dx$

(12)$\displaystyle ∫x^3\sqrt{x^2+2}\,dx$

Réponse: $\displaystyle ∫x^3\sqrt{x^2+2}\,dx = \frac{1}{15}(x^2+2)^{3/2}(3x^2−4)+C$

13)$\displaystyle ∫\frac{3x^2+1}{x^4−2x^3−x^2+2x}\,dx$

(14)$\displaystyle ∫\frac{1}{x^4+4}\,dx$

Réponse: $\displaystyle ∫\frac{1}{x^4+4}\,dx = \frac{1}{16}\ln(\frac{x^2+2x+2}{x^2−2x+2})−\frac{1}{8}\tan^{−1}(1−x)+\frac{1}{8}\tan^{−1}(x+1)+C$

(15)$\displaystyle ∫\frac{\sqrt{3+16x^4}}{x^4}\,dx$

Dans les exercices 16 à 18, approximez les intégrales en utilisant la règle du point médian, la règle trapézoïdale et la règle de Simpson en utilisant quatre sous-intervalles, arrondis à trois décimales.

16) [T]$\displaystyle ∫^2_1\sqrt{x^5+2}\,dx$

Réponse: $M_4=3.312,$
$T_4=3.354,$
$S_4=3.326$

17) [T]$\displaystyle ∫^{\sqrt{π}}_0e^{−\sin(x^2)}\,dx$

18) [T]$\displaystyle ∫^4_1\frac{\ln(1/x)}{x}\,dx$

Réponse: $M_4=−0.982,$
$T_4=−0.917,$
$S_4=−0.952$

Dans les exercices 19 à 20, évaluez les intégrales, si possible.

19)$\displaystyle ∫^∞_1\frac{1}{x^n}\,dx,$ pour quelles valeurs de cette intégrale$n$ convergent-elles ou divergent-elles ?

(20)$\displaystyle ∫^∞_1\frac{e^{−x}}{x}\,dx$

Réponse: environ 0,2194

Dans les exercices 21 à 22, considérez la fonction gamma donnée par$\displaystyle Γ(a)=∫^∞_0e^{−y}y^{a−1}\,dy.$

21) Montrez que$\displaystyle Γ(a)=(a−1)Γ(a−1).$

22) Étendre pour montrer que l'$\displaystyle Γ(a)=(a−1)!,$hypothèse$a$ est un entier positif.

La voiture la plus rapide au monde, la Bugati Veyron, peut atteindre une vitesse maximale de 408 km/h. Le graphique représente sa vitesse.

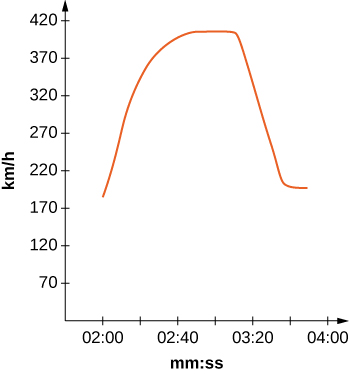
$Cette figure comporte un graphique dans le premier quadrant. Il augmente jusqu'à l'endroit où x est d'environ 03:00 mm:ss, puis descend abruptement. La hauteur maximale du graphique, ici la chute se produit, est d'environ 420 km/h.$

23) [T] Utilisez le graphique pour estimer la vitesse toutes les 20 secondes et l'ajuster à un graphique de la forme$v(t)=ae^{bx}\sin(cx)+d.$ (Conseil : considérez les unités de temps.)

24) [T] À l'aide de la fonction du problème précédent, déterminez exactement la distance parcourue par la Bugati Veyron au cours des 1 min 40 secondes incluses dans le graphique.

Réponse: Les réponses peuvent varier. Ex :$9.405$ km