5.4E : Exercices pour la section 5.4

Last updated
Save as PDF

Page ID: 197377

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Dans les exercices 1 à 6, utilisez des formules d'intégration de base pour calculer les antidérivés suivants.

1)$\displaystyle ∫\left(\sqrt{x}−\frac{1}{\sqrt{x}}\right)\,dx$

Réponse: $\displaystyle ∫\left(\sqrt{x}−\frac{1}{\sqrt{x}}\right)\,dx=∫x^{1/2}\,dx−∫x^{−1/2}\,dx=\frac{2}{3}x^{3/2}+C_1−2x^{1/2+}C_2=\frac{2}{3}x^{3/2}−2x^{1/2}+C$

2)$\displaystyle ∫\left(e^{2x}−\frac{1}{2}e^{x/2}\right)\,dx$

3)$\displaystyle ∫\frac{dx}{2x}$

Réponse: $\displaystyle ∫\frac{dx}{2x}=\frac{1}{2}\ln|x|+C$

4)$\displaystyle ∫\frac{x−1}{x^2}\,dx$

5)$\displaystyle ∫^π_0(\sin x−\cos x)\,dx$

Réponse: $\displaystyle ∫^π_0\sin x\,dx−∫^π_0\cos x\,dx=−\cos x\big|^π_0−(\sin x)\big|^π_0=(−(−1)+1)−(0−0)=2$

6)$\displaystyle ∫^{π/2}_0(x−\sin x)\,dx$

7) Écrivez une intégrale qui exprime l'augmentation du périmètre$P(s)$ d'un carré lorsque la longueur de son côté$s$ passe de 2 unités à 4 unités et évaluez l'intégrale.

Réponse: $P(s)=4s,$donc$\dfrac{dP}{ds}=4$ et$\displaystyle ∫^4_24\,ds=8.$

8) Écrivez une intégrale qui quantifie la variation de l'aire$A(s)=s^2$ d'un carré lorsque la longueur du côté double d'une$S$$2S$ unité à l'autre et évaluez l'intégrale.

9) Un$N$ -gon régulier (polygone à côtés dont les côtés ont la même longueur$s$, tel qu'un pentagone ou un hexagone) a un périmètre$Ns.$ Écrivez une intégrale qui exprime l'augmentation du périmètre d'un$N$ -gon régulier lorsque la longueur de chaque côté augmente de 1 unité à 2 unités$N$ et évaluez l'intégrale.

Réponse: $\displaystyle ∫^2_1N\,ds=N$

10) L'aire d'un pentagone régulier de longueur latérale$a>0$ est$pa^2$ de$p=\frac{1}{4}\sqrt{5+\sqrt{5+2\sqrt{5}}}$. Le Pentagone à Washington, DC, a des côtés intérieurs d'une longueur de 360 pieds et des côtés extérieurs d'une longueur de 920 pieds. Écrivez une intégrale pour exprimer la surface du toit du Pentagone en fonction de ces dimensions et évaluez cette zone.

11) Un dodécaèdre est un solide platonicien dont la surface est composée de 12 pentagones, chacun de surface égale. Dans quelle mesure la surface d'un dodécaèdre augmente-t-elle lorsque la longueur des côtés de chaque pentagone double, passant de 1 à 2 unités ?

Réponse: $p$Comme dans l'exercice précédent, la surface de chacun des 12 pentagones augmente de$2p$ à$4p$ unités, de sorte que l'augmentation nette de la surface du dodécaèdre est en$36p$ unités.

12) Un icosaèdre est un solide platonicien dont la surface est composée de 20 triangles équilatéraux. Dans quelle mesure la surface d'un icosaèdre augmente-t-elle lorsque la longueur latérale de chaque triangle double, passant d'une unité à une$2a$ unité ?

13) Écrivez une intégrale qui quantifie la variation de l'aire de la surface d'un cube lorsque la longueur de son côté double d'une$s$$2s$ unité à l'autre et évaluez l'intégrale.

Réponse: $\displaystyle 18s^2=6∫^{2s}_s 2x\,dx$

14) Écrivez une intégrale qui quantifie l'augmentation du volume d'un cube lorsque la longueur du côté double d'une$s$$2s$ unité à l'autre et évaluez l'intégrale.

15) Écrivez une intégrale qui quantifie l'augmentation de la surface d'une sphère lorsque son rayon double d'une$R$$2R$ unité à l'autre et évaluez l'intégrale.

Réponse: $\displaystyle 12πR^2=8π∫^{2R}_Rr\,dr$

16) Écrivez une intégrale qui quantifie l'augmentation du volume d'une sphère lorsque son rayon double d'une$R$$2R$ unité à l'autre et évaluez l'intégrale.

17) Supposons qu'une particule se déplace le long d'une ligne droite avec une vitesse$v(t)=4−2t,$ où$0≤t≤2$ (en mètres par seconde). Trouvez le déplacement dans le temps$t$ et la distance totale parcourue jusqu'à$t=2.$

Réponse: $\displaystyle d(t)=∫^t_0v(s)\,ds=4t−t^2.$La distance totale est$d(2)=4$ de m.

18) Supposons qu'une particule se déplace le long d'une ligne droite dont la vitesse est définie par l'$v(t)=t^2−3t−18,$endroit$0≤t≤6$ (en mètres par seconde). Trouvez le déplacement dans le temps$t$ et la distance totale parcourue jusqu'à$t=6.$

19) Supposons qu'une particule se déplace le long d'une ligne droite dont la vitesse est définie par l'$v(t)=|2t−6|,$endroit$0≤t≤6$ (en mètres par seconde). Trouvez le déplacement dans le temps$t$ et la distance totale parcourue jusqu'à$t=6.$

Réponse: $\displaystyle d(t)=∫^t_0v(s)\,ds.$$t<3,\;d(t)=∫^t_0(6−2t)\,dt=6t−t^2.$Pour$\displaystyle t>3,\;d(t)=d(3)+∫^t_3(2t−6)\,dt=9+(t^2−6t).$ La distance totale est$d(6)=9$ de m.

20) Supposons qu'une particule se déplace le long d'une ligne droite avec une accélération définie par l'$a(t)=t−3,$endroit$\displaystyle 0≤t≤6$ (en mètres par seconde). Trouvez la vitesse et le déplacement dans le temps$t$ et la distance totale parcourue jusqu'à$t=6$ si$v(0)=3$ et$ d(0)=0.$

21) Une balle est lancée vers le haut d'une hauteur de 1,5 m à une vitesse initiale de 40 m/sec. L'accélération résultant de la gravité$−9.8\, \text{m/sec}^2.$ néglige la résistance de l'air, déterminez la vitesse$v(t)$ et la hauteur$h(t)$ de la balle$t$ quelques secondes après son lancement et avant qu'elle ne revienne au sol.

Réponse: $v(t)=40−9.8t;\; h(t)=1.5+40t−4.9t^2$m/s

22) Une balle est lancée vers le haut d'une hauteur de 3 m à une vitesse initiale de 60 m/sec. L'accélération résultant de la gravité est$−9.8 \, \text{m/sec}^2$. En négligeant la résistance de l'air, déterminez la vitesse$v(t)$ et la hauteur$h(t)$ de la balle$t$ quelques secondes après son lancement et avant qu'elle ne revienne au sol.

23) La zone$A(t)$ de forme circulaire croît à un rythme constant. Si la surface augmente d'$4π$unités en$9π$ unités entre les temps$t=2$ et$t=3,$ trouvez la variation nette du rayon pendant cette période.

Réponse: L'augmentation nette est de 1 unité.

24) Un ballon sphérique est gonflé à une vitesse constante. Si le volume du ballon change$288π \text{ in}^3$ entre le temps$t=30$ et les$t=60$ secondes, déterminez la variation nette du rayon du ballon pendant cette période.$36π \text{ in}^3$

25) L'eau s'écoule dans un réservoir conique avec une section transversale$πx^2$ en hauteur$x$ et un volume$\frac{πx^3}{3}$ allant jusqu'à la hauteur$x.$ Si l'eau s'écoule dans le réservoir à un débit de 1,$\text{m}^3\text{/min},$ trouvez la hauteur de l'eau dans le réservoir après 5 minutes. Détermine le changement de hauteur entre 5 min et 10 min.

Réponse: À$t=5$, la hauteur de l'eau est de$x=\left(\frac{15}{π}\right)^{1/3}$ m. La variation nette de hauteur de$t=5$ à$t=10$ est de$\left(\left(\frac{30}{π}\right)^{1/3}−\left(\frac{15}{π}\right)^{1/3}\right)$ m.

26) Un réservoir cylindrique horizontal a une section transversale$A(x)=4(6x−x^2)\,\text{m}^2$ à une hauteur de$x$ mètres au-dessus du fond lorsque$x≤3.$

a. Le volume$V$ entre les hauteurs$a$ et$b$ est$\displaystyle ∫^b_aA(x)\,dx.$ Trouvez le volume à des hauteurs comprises entre 2 m et 3 m.

b. Supposons que de l'huile soit pompée dans le réservoir à un débit de 50 L/min. Selon la règle de la chaîne,$\dfrac{dx}{dt}=\dfrac{dx}{dV}\dfrac{dV}{dt},$ à combien de mètres par minute la hauteur d'huile dans le réservoir$x,$ change-t-elle, exprimée en$x$ mètres ?

c. Combien de temps faut-il pour remplir le réservoir à 3 m à partir d'un niveau de remplissage de 2 m ?

27) Le tableau suivant répertorie la puissance électrique en gigawatts, c'est-à-dire le taux auquel l'énergie est consommée, utilisée dans une ville donnée à différentes heures de la journée, sur une période typique de 24 heures, l'heure 1 correspondant de minuit à 1 heure du matin.

Heure	Pouvoir	Heure	Pouvoir
1	28	13	48
2	25	14	49
3	24	15	49
4	23	16	50
5	24	17	50
6	27	18	50
7	29	19	46
8	32	20	43
9	34	21	42
10	39	22	40
11	42	23	37
12	46	24	34

Déterminez la quantité totale d'énergie en gigawattheures (GW-h) consommée par la ville sur une période typique de 24 heures.

Réponse: La consommation électrique quotidienne totale est estimée comme la somme des débits horaires, soit 911 GWh.

28) La consommation moyenne d'énergie électrique résidentielle (en centaines de watts) par heure est indiquée dans le tableau suivant.

Heure	Pouvoir	Heure	Pouvoir
1	8	13	12
2	6	14	13
3	5	15	14
4	4	16	15
5	5	17	17
6	6	18	19
7	7	19	18
8	8	20	17
9	9	21	16
10	10	22	16
11	10	23	13
12	11	24	11

a. Calculez l'énergie totale moyenne consommée par jour en kilowattheures (kWh).

b. Si une tonne de charbon produit 1 842 kWh, combien de temps faut-il à une résidence moyenne pour brûler une tonne de charbon ?

c. Expliquer pourquoi les données peuvent correspondre à un tracé du formulaire$p(t)=11.5−7.5\sin\left(\frac{πt}{12}\right).$

29) Les données du tableau suivant sont utilisées pour estimer la puissance moyenne produite par Peter Sagan pour chacune des 18 dernières secondes de la première étape du Tour de France 2012.

Deuxième	Watts	Deuxième	Watts
1	600	10	1200
2	500	11	1170
3	575	12	1125
4	1050	13	1100
5	925	14	1075
6	950	15	1000
7	1050	16	950
8	950	17	900
9	1100	18	780

Source de puissance de sortie moyenne : sportsexercisengineering.com

Estimez l'énergie nette utilisée en kilojoules (kJ), en notant que 1 W = 1 J/s, et la puissance moyenne produite par Sagan pendant cet intervalle de temps.

Réponse: $17$kJ

30) Les données du tableau suivant sont utilisées pour estimer la puissance moyenne produite par Peter Sagan pour chaque intervalle de 15 minutes de la première étape du Tour de France 2012.

Minutes	Watts	Minutes	Watts
15	200	165	170
30	180	180	220
45	190	195	140
60	230	210	225
75	240	225	170
90	210	240	10
105	210	255	200
1120	220	270	220
135	210	285	250
150	150	300	400

Source de puissance de sortie moyenne : sportsexercisengineering.com

Estimez l'énergie nette utilisée en kilojoules, en notant que 1 W = 1 J/s.

31) La répartition des revenus en 2012 aux États-Unis par tranches de 5 000 dollars est donnée dans le tableau suivant. La 5ème rangée indique le pourcentage de ménages dont les revenus se situent entre$$5000xk$ et$5000xk+4999$. La rangée$k=40$ contient tous les ménages dont le revenu se situe entre 200 000$ et 250 000$ et$k=41$ représente tous les ménages dont le revenu est supérieur à 250 000$.

0	3.5	21	1,5
1	4.1	22	1.4
2	5,9	23	1.3
3	5.7	24	1.3
4	5,9	25	1.1
5	5.4	26	1,0
6	5.5	27	0,75
7	5.1	28	0,8
8	4.8	29	1,0
9	4.1	30	0,6
10	4.3	31	0,6
11	3.5	32	5.
12	3.7	33	0,5
13	3.2	34	0,4
14	3,0	35	0,3
15	2,8	36	0,3
16	2,5	37	0,3
17	2.2	38	0,2
18	2.2	39	1,8
19	1,8	40	2.3
20	2.1	41

Distributions de revenusSource : http://www.census.gov/prod/2013pubs/p60-245.pdf

a. Estimez le pourcentage de ménages américains en 2012 dont le revenu était inférieur à 55 000 dollars.

b. Quel pourcentage de ménages avaient un revenu supérieur à 85 000$ ?

c. Tracez les données et essayez d'adapter leur forme à celle d'un graphique du formulaire$a(x+c)e^{−b(x+e)}$ pour$a,\, b,\, c.$

Réponse

a. 54,3 % ;
b. 27,00 % ;
c. La courbe du diagramme suivant est$2.35(t+3)e^{−0.15(t+3)}.$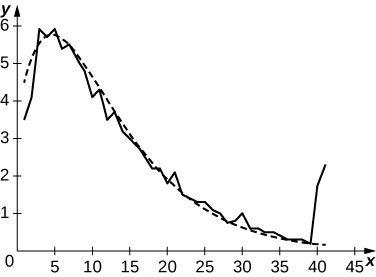

$Un graphique des données et une fonction approximative des données. La fonction est une approximation très proche.$

32) La loi de la gravité de Newton stipule que la force gravitationnelle exercée par un objet de masse$M$ et un objet de masse$m$ dont les centres sont séparés par une distance r est$F=G\dfrac{mM}{r^2}$, avec$G$ une constante empirique$G=6.67x10^{−11}\,\text{m}^3/(\text{kg⋅s}^2)$. Le travail effectué par une force variable sur un intervalle$ [a,b]$ est défini comme$\displaystyle W=∫^b_aF(x)\,dx$. Si la Terre a une masse$5.97219×10^{24}$ et un rayon de 6371 km, calculez la quantité de travail nécessaire pour élever un satellite météorologique polaire d'une masse de 1 400 kg à son altitude orbitale de 850 km au-dessus de la Terre.

33) Pour un véhicule à moteur donné, la décélération maximale pouvant être atteinte par freinage est approximativement$7 \text{ m/sec}^2$ sur du béton sec. Sur asphalte mouillé, il est approximativement$2.5 \text{ m/sec}^2.$ Étant donné que 1 mi/h correspond à 0,447 m/sec, déterminez la distance totale parcourue par une voiture en mètres sur du béton sec après avoir serré les freins jusqu'à l'arrêt complet si la vitesse initiale est de 67 mi/h (30 m/sec) ou si la vitesse de freinage initiale est de 56 mi/h (25 m/s). Déterminez les distances correspondantes si la surface est recouverte d'asphalte humide et glissant.

Réponse: Dans des conditions sèches, avec une vitesse initiale$v_0=30$ m/s,$D=64.3$ et, si$v_0=25,\; D=44.64$. Dans des conditions humides$v_0=30$, si$D=180$ et si$v_0=25,\;D=125.$

34) John est un homme de 25 ans qui pèse 160 livres. Il brûle des$500−50t$ calories à l'heure en faisant du vélo pendant des$t$ heures. Si un biscuit à l'avoine contient 55 calories et que John mange$4t$ des biscuits pendant l'$t^{\text{th}}$heure, combien de calories nettes a-t-il perdues après 3 heures de vélo ?

35) Sandra est une femme de 25 ans qui pèse 120 livres. Elle brûle$300−50t$ cal/h en marchant sur son tapis roulant pendant des$t$ heures. Son apport calorique en buvant du Gatorade est de$100t$ calories pendant l'$t^{\text{th}}$heure. Quelle est sa diminution nette de calories après 3 heures de marche ?

Réponse: 225 cal

36) Un véhicule à moteur a une efficacité maximale de 33 mi/gal à une vitesse de croisière de 40 mi/h. L'efficacité diminue à une vitesse de 0,1 mpg/mph entre 40 mi/h et 50 mi/h, et à une vitesse de 0,4 mpg/mph entre 50 mi/h et 80 mi/h. Quelle est l'efficacité en miles par gallon si la voiture roule à 50 mi/h ? Quelle est l'efficacité en miles par gallon si la voiture roule à 130 km/h ? Si l'essence coûte 3,50 $/gal, quel est le coût du carburant pour parcourir 80 miles à 40 mi/h, à 50 mi/h et à 80 mi/h ?

37) Bien que certains moteurs soient plus efficaces à une puissance donnée que d'autres, en moyenne, le rendement énergétique diminue avec la puissance à un taux de$1/25$ mpg/cheval-vapeur. Si un moteur typique de 50 chevaux a un rendement énergétique moyen de 32 mi/gal, quel est le rendement énergétique moyen d'un moteur de la puissance suivante : 150, 300, 450 ?

Réponse: $ E(150)=28,\;E(300)=22,\;E(450)=16$

38) [T] Le tableau suivant présente le barème 2013 de l'impôt fédéral sur le revenu par rapport au revenu imposable.

Fourchette de revenu imposable	La taxe est...	... Du montant supérieur
0$ à 8 925$	10 %	0$
8925$ — 36 250$	892,50$ + 15 %	8 925$
36 250$ à 87 850$	4 991,25$ + 25 %	36 250$
87 850$ — 183 250$	17 891,25$ + 28 %	87 850 DOLLARS
183 250$ — 398 350$	44 603,25$ + 33 %	183 250$
398 350$ — 400 000$	115 586,25$ + 35 %	398 350$
> 400 000$	116 163,75$ + 39,6 %	400 000$

Impôt fédéral sur le revenu par rapport au revenu imposableSource : http://www.irs.gov/pub/irs-prior/i1040tt--2013.pdf.

Supposons que Steve vient de recevoir une augmentation de 10 000$. Quelle part de cette augmentation reste-t-il après impôts fédéraux si le salaire de Steve avant de recevoir l'augmentation était de 40 000 dollars ? Si c'était 90 000 dollars ? Si c'était 385 000$ ?

39) [T] Le tableau suivant fournit des données hypothétiques concernant le niveau de service sur une certaine autoroute.

Plage de vitesse sur autoroute (mi/h)	Véhicules par heure et par voie	Plage de densité (véhicules/km)
>60	< 600	<10
60-57	300-1000	10-20
57-54	1000-1500	20-30
57-54	1500-1900	30-45
46-30	1900-2100	48-70
<30	Instable	70-200

a. Tracez les véhicules par heure et par voie sur l'$x$axe Y et la vitesse de l'autoroute sur$y$ l'axe.

b. Calculez la diminution moyenne de la vitesse (en miles par heure) par unité d'augmentation de la congestion (véhicules par heure et par voie) lorsque cette dernière augmente de 600 à 1 000, de 1 000 à 1 500 et de 1 500 à 2 100. La diminution du nombre de miles par heure dépend-elle de façon linéaire de l'augmentation du nombre de véhicules par heure et par voie ?

c. Tracez les minutes par mile (60 fois l'inverse des miles par heure) en fonction du nombre de véhicules par heure et par voie. Cette fonction est-elle linéaire ?

Réponse

un.

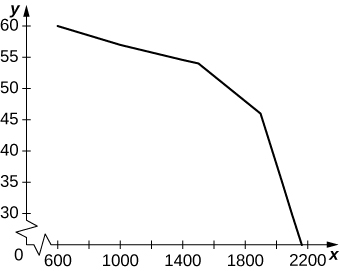
$Un diagramme des données données, qui décroît de manière approximativement concave vers le bas de 600 à 2200.$

b. Entre 600 et 1 000, la diminution moyenne du nombre de véhicules par heure et par voie est de −0,0075. Entre 1 000 et 1 500, il est de −0,006 par véhicule par heure et par voie, et entre 1 500 et 2 100, il est de −0,04 véhicule par heure et par voie.

c.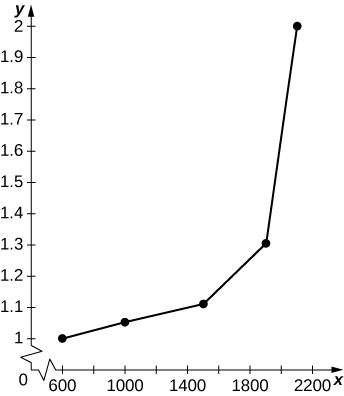

$Un graphique de données données, montrant que le nombre de minutes par kilomètre augmente de façon spectaculaire à mesure que le nombre de véhicules par heure atteint 2 000.$

Le graphique n'est pas linéaire, les minutes par mile augmentant de façon spectaculaire à mesure que le nombre de véhicules par heure et par voie atteint 2 000.

Pour les deux exercices suivants, utilisez les données du tableau suivant, qui montre les populations de pygargues à tête blanche de 1963 à 2000 dans la zone continentale des États-Unis.

Année	Population de couples reproducteurs d'aigles à tête blanche
1963	487
1974	791
1981	1188
1986	1875
1992	3749
1996	5094
2000	6471

Population de couples reproducteurs de pygargues à tête blanche Source : http://www.fws.gov/Midwest/eagle/pop... /chtofprs.html.

40) [T] Le graphique ci-dessous trace le quadratique par$p(t)=6.48t^2−80.31t+585.69$ rapport aux données du tableau précédent, normalisé de manière à$t=0$ correspondre à 1963. Estimez le nombre moyen de pygargues à tête blanche présents par an pendant 37 ans en calculant la valeur moyenne de$p$ plus de$[0,37].$

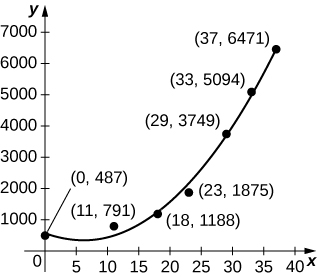
$Un graphique des données et une fonction quadratique qui les rapproche de près.$

41) [T] Le graphique ci-dessous représente le cube par$p(t)=0.07t^3+2.42t^2−25.63t+521.23$ rapport aux données du tableau précédent, normalisé de manière à$t=0$ correspondre à 1963. Estimez le nombre moyen de pygargues à tête blanche présents par an pendant 37 ans en calculant la valeur moyenne de$p$ plus de$[0,37].$

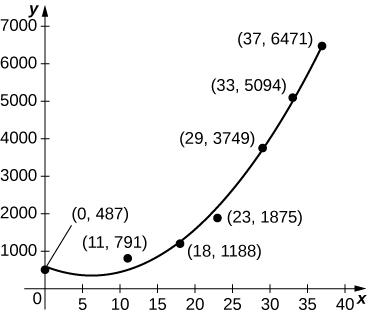
$Un graphique des données et une fonction cubique qui s'en rapproche de près.$

Réponse: $\displaystyle \frac{1}{37}∫^{37}_0p(t)\,dt=\frac{0.07(37)^3}{4}+\frac{2.42(37)^2}{3}−\frac{25.63(37)}{2}+521.23≈2037$

Solution :

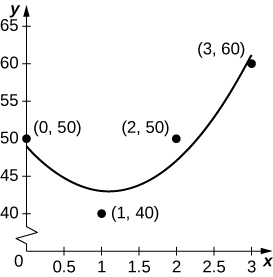
42) [T] Supposons que vous partiez en voyage en voiture et que vous enregistrez votre vitesse toutes les demi-heures, comme indiqué dans le tableau suivant. Le meilleur ajustement quadratique des données est$q(t)=5x^2−11x+49$ indiqué dans le graphique ci-joint. Intégrez$q$ pour estimer la distance totale parcourue au cours des 3 heures.

Heure (heure)	Vitesse (m [h)
0 (début)	50
1	40
2	50
3	60

$Un graphique des données et une courbe destinée à les approximer.$

Lorsqu'une voiture accélère, elle n'accélère pas à un rythme constant ; l'accélération est plutôt variable. Pour les exercices suivants, utilisez le tableau suivant, qui contient l'accélération mesurée à chaque seconde lorsqu'un conducteur se dirige vers une autoroute.

Durée (sec)	Accélération (m2/sec)
1	11.2
2	10,6
3	8.1
4	5.4
5	0

43) [T] Le graphique ci-joint représente le meilleur ajustement quadratique,$a(t)=−0.70t^2+1.44t+10.44$, par rapport aux données du tableau précédent. Calculez la valeur moyenne de$a(t)$ pour estimer l'accélération moyenne entre$t=0$ et$t=5.$

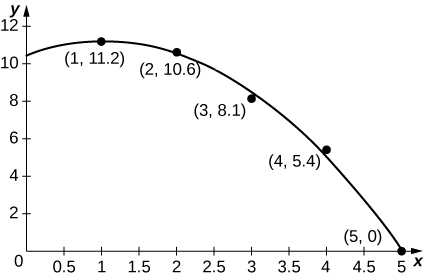
$Un graphique des données et une courbe qui se rapproche étroitement des données.$

Réponse: L'accélération moyenne est de$\displaystyle A=\frac{1}{5}∫^5_0a(t)\,dt=−\frac{0.7(5^2)}{3}+\frac{1.44(5)}{2}+10.44≈8.2$ Mph/s

44) [T] À l'aide de l'équation d'accélération de l'exercice précédent, trouvez l'équation de vitesse correspondante. En supposant que la vitesse finale est de 0 mph, déterminez la vitesse à l'heure$t=0.$

45) [T] À l'aide de l'équation de vitesse de l'exercice précédent, trouvez l'équation de distance correspondante, en supposant que votre distance initiale est de 0 mi. Quelle distance avez-vous parcourue en accélérant votre voiture ? (Conseil : vous devrez convertir les unités de temps.)

Réponse: $\displaystyle d(t)=∫^1_0|v(t)|\,dt=∫^t_0\left(\frac{7}{30}t^3−0.72t^2−10.44t+41.033\right)\,dt=\frac{7}{120}t^4−0.24t^3−5.22t^3+41.033t.$Ensuite, les$d(5)≈81.12 \,\text{mph} × \text{sec}≈119$ pieds.

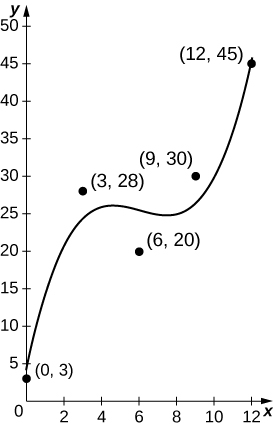
46) [T] Le nombre de hamburgers vendus dans un restaurant tout au long de la journée est indiqué dans le tableau suivant, le graphique ci-joint représentant le meilleur ajustement cubique des données,$b(t)=0.12t^3−2.13t^3+12.13t+3.91,$$t=0$ correspondant à 9 heures du matin et$t=12$ correspondant à 21 heures. Calculez la valeur moyenne$b(t)$ de estimer le nombre moyen de hamburgers vendus par heure.

Quelques heures après minuit	Nombre de hamburgers vendus
9	3
12	28
15	20
18	30
21	45

$Une carte des données et une courbe destinées à approximer les données.$

47) [T] Une athlète passe devant un détecteur de mouvement qui enregistre sa vitesse, comme indiqué dans le tableau suivant. Le meilleur ajustement linéaire à ces données,$ℓ(t)=−0.068t+5.14$, est indiqué dans le graphique ci-joint. Utilisez la valeur moyenne comprise$ℓ(t)$ entre$t=0$ et$t=40$ pour estimer la vitesse moyenne du coureur.

Minutes	Vitesse (m/sec)
0	5
10	4.8
20	3.6
30	3,0
40	2,5

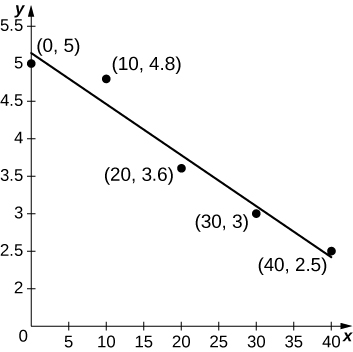
$Un graphique des données et une ligne pour approximer les données.$

Réponse: $\displaystyle \tfrac{1}{40} ∫^{40}_0(−0.068t+5.14)\,dt=−\frac{0.068(40)}{2}+5.14=3.78$ m/sec