4.8 : La règle de L'Hôpital
- Page ID
- 197673
- Sachez quand appliquer la règle de L'Hôpital.
- Identifiez les formes indéterminées produites par les quotients, les produits, les soustractions et les puissances, et appliquez la règle de L'Hôpital dans chaque cas.
- Décrivez les taux de croissance relatifs des fonctions.
Dans cette section, nous examinons un puissant outil d'évaluation des limites. Cet outil, connu sous le nom de règle de L'Hôpital, utilise des dérivés pour calculer les limites. Avec cette règle, nous serons en mesure d'évaluer de nombreuses limites que nous n'avons pas encore pu déterminer. Au lieu de nous appuyer sur des preuves numériques pour supposer qu'une limite existe, nous serons en mesure de démontrer définitivement qu'une limite existe et de déterminer sa valeur exacte.
Appliquer la règle de L'Hôpital
La règle de L'Hôpital peut être utilisée pour évaluer les limites impliquant le quotient de deux fonctions. Considérez
\[\lim_{x→a}\dfrac{f(x)}{g(x)}. \nonumber \]
Si\(\displaystyle \lim_{x→a}f(x)=L_1\) et\(\displaystyle \lim_{x→a}g(x)=L_2≠0,\) alors
\[\lim_{x→a}\dfrac{f(x)}{g(x)}=\dfrac{L_1}{L_2}. \nonumber \]
Cependant, que se passe-t-il si\(\displaystyle \lim_{x→a}f(x)=0\) et\(\displaystyle \lim_{x→a}g(x)=0\) ? C'est ce que nous appelons l'une des formes indéterminées, de type\(\dfrac{0}{0}\). Ceci est considéré comme une forme indéterminée car nous ne pouvons pas déterminer le comportement exact du SA\(\dfrac{f(x)}{g(x)}\)\(x→a\) sans une analyse plus approfondie. Nous en avons vu des exemples plus tôt dans le texte. Par exemple, considérez
\[\lim_{x→2}\dfrac{x^2−4}{x−2} \nonumber \]
et
\[\lim_{x→0}\dfrac{\sin x}{x}.\nonumber \]
Pour le premier de ces exemples, nous pouvons évaluer la limite en factorisant le numérateur et en écrivant
\[\lim_{x→2}\dfrac{x^2−4}{x−2}=\lim_{x→2}\dfrac{(x+2)(x−2)}{x−2}=\lim_{x→2}(x+2)=2+2=4. \nonumber \]
Car\(\displaystyle \lim_{x→0}\dfrac{\sin x}{x}\) nous avons pu montrer, à l'aide d'un argument géométrique, que
\[\lim_{x→0}\dfrac{\sin x}{x}=1. \nonumber \]
Nous utilisons ici une technique différente pour évaluer de telles limites. Non seulement cette technique permet d'évaluer plus facilement ces limites, mais elle nous permet également, et surtout, d'évaluer de nombreuses autres limites que nous ne pouvions pas calculer auparavant.
L'idée qui sous-tend la règle de L'Hôpital peut être expliquée à l'aide d'approximations linéaires locales. Considérez deux fonctions dérivables\(f\) et\(g\) telles que\(\displaystyle \lim_{x→a}f(x)=0=\lim_{x→a}g(x)\) et telles que\(g′(a)≠0\) Pour\(x\) près\(a\), nous pouvons écrire
\[f(x)≈f(a)+f′(a)(x−a) \nonumber \]
et
\[g(x)≈g(a)+g′(a)(x−a). \nonumber \]
Par conséquent,
\[\dfrac{f(x)}{g(x)}≈\dfrac{f(a)+f′(a)(x−a)}{g(a)+g′(a)(x−a)}. \nonumber \]
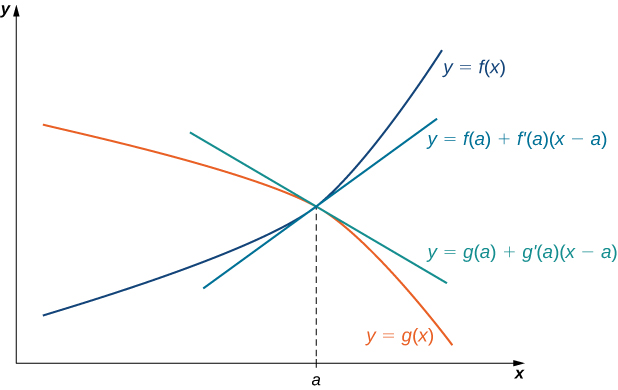
Puisque\(f\) est différenciable à\(a\), alors\(f\) est continu à\(a\), et donc\(\displaystyle f(a)=\lim_{x→a}f(x)=0\). De même,\(\displaystyle g(a)=\lim_{x→a}g(x)=0\). Si nous supposons également que\(f′\) et que nous\(g′\) sommes continus à\(x=a\), alors\(\displaystyle f′(a)=\lim_{x→a}f′(x)\) et\(\displaystyle g′(a)=\lim_{x→a}g′(x)\). En utilisant ces idées, nous concluons que
\[\lim_{x→a}\dfrac{f(x)}{g(x)}=\lim_{x→a}\dfrac{f′(x)(x−a)}{g′(x)(x−a)}=\lim_{x→a}\dfrac{f′(x)}{g′(x)} . \nonumber \]
Notez que l'hypothèse selon laquelle\(f′\) et\(g′\) sont continus\(a\) et\(g′(a)≠0\) peut être assouplie. Nous énonçons formellement la règle de L'Hôpital pour la forme indéterminée\(\dfrac{0}{0}\). Notez également que la notation\(\dfrac{0}{0}\) ne signifie pas que nous divisons réellement zéro par zéro. Nous utilisons plutôt la notation\(\dfrac{0}{0}\) pour représenter un quotient de limites, chacune étant nulle.
Supposons\(f\) et\(g\) sont des fonctions dérivables sur un intervalle ouvert contenant\(a\), sauf éventuellement, à\(a\). Si\(\displaystyle \lim_{x→a}f(x)=0\) et\(\displaystyle \lim_{x→a}g(x)=0,\) alors
\[\lim_{x→a}\dfrac{f(x)}{g(x)}=\lim_{x→a}\dfrac{f′(x)}{g′(x)}, \nonumber \]
en supposant que la limite du droit existe\(∞\) ou est\(−∞\). Ce résultat est également valable si nous envisageons des limites unilatérales, ou si\(a=∞\) ou\(a=−∞.\)
Nous fournissons une preuve de ce théorème dans le cas particulier où\(f,g,f′,\) et\(g′\) sont tous continus sur un intervalle ouvert contenant\(a\). Dans ce cas, puisque\(\displaystyle\lim_{x→a}f(x)=0=\lim_{x→a}g(x)\) et\(f\) et\(g\) sont continus à\(a\), il s'ensuit que\(f(a)=0=g(a)\). Par conséquent,
\ [\ begin {align*} \ lim_ {x→a} \ dfrac {f (x)} {g (x)} &= \ lim_ {x→a} \ dfrac {f (x) −f (a)} {g (x) −g (a)} & & \ text {Depuis} \, f (a) =0=g (a) \ \ [4pt]
&= \ lim_ {x→a} \ dfrac {\ dfrac {f (x) −f (a)} {x−a}} {\ dfrac {g (x) −g (a)} {x−a}} & & \ text {Multipliez le numérateur et le dénominateur par} \, \ frac {1} {x-a} \ \ [4pt]
&= \ frac {\ displaystyle \ lim_ {x→a} \ dfrac {f (x) −f (a)} {x−a}} {\ displaystyle \ lim_ {x→a} \ dfrac {g (x) −g (a)} {x−a}} & \ text {La limite d'un quotient est le quotient des limites.} \ \ [4−a} pt]
&= \ dfrac {f′ (a)} {g′ (a)} & & \ text {Par la définition du dérivé} \ \ [4pt]
&= \ frac {\ displaystyle \ lim_ {x→a} f′ (x)} {\ displaystyle \ lim_ {x→a} g′ (x)} & & \ text {Par la continuité de} \, f′ \, \ text {et} \, g′ \ \ [4pt]
&= \ lim_ {x→a} \ dfrac {f′ (x)} {g′ ′ (x)}. & & \ text {La limite d'un quotient} \ end {align*} \]
Notez que la règle de L'Hôpital stipule que l'on peut calculer la limite d'un quotient\(\dfrac{f}{g}\) en tenant compte de la limite du quotient des dérivés\(\dfrac{f′}{g′}\). Il est important de comprendre que nous ne calculons pas la dérivée du quotient\(\dfrac{f}{g}\).
□
Évaluez chacune des limites suivantes en appliquant la règle de L'Hôpital.
- \(\displaystyle \lim_{x→0}\dfrac{1−\cos x}{x}\)
- \(\displaystyle \lim_{x→1}\dfrac{\sin(πx)}{\ln x}\)
- \(\displaystyle \lim_{x→∞}\dfrac{e^{1/x}−1}{1/x}\)
- \(\displaystyle \lim_{x→0}\dfrac{\sin x−x}{x^2}\)
Solution
a. Depuis le numérateur\(1−\cos x→0\) et le dénominateur\(x→0\), nous pouvons appliquer la règle de L'Hôpital pour évaluer cette limite. Nous avons
\[\lim_{x→0}\dfrac{1−\cos x}{x}=\lim_{x→0}\dfrac{\dfrac{d}{dx}\big(1−\cos x\big)}{\dfrac{d}{dx}\big(x\big)}=\lim_{x→0}\dfrac{\sin x}{1}=\frac{\displaystyle \lim_{x→0}\sin x}{\displaystyle \lim_{x→0}1}=\dfrac{0}{1}=0. \nonumber \]
b. En tant\(x→1,\) que numérateur\(\sin(πx)→0\) et dénominateur Nous pouvons\(\ln(x)→0.\) donc appliquer la règle de L'Hôpital. Nous obtenons
\[\begin{align*} \lim_{x→1}\dfrac{\sin(πx)}{\ln x}&=\lim_{x→1}\dfrac{π \cos(πx)}{1/x} \\[4pt] &=\lim_{x→1}(πx)\cos(πx) \\[4pt] &=(π⋅1)(−1)=−π. \end{align*} \nonumber \]
c. As\(x→∞\), le numérateur\(e^{1/x}−1→0\) et le dénominateur\(\frac{1}{x}→0\). Nous pouvons donc appliquer la règle de L'Hôpital. Nous obtenons
\[\lim_{x→∞}\dfrac{e^{1/x}−1}{\dfrac{1}{x}}=\lim_{x→∞}\dfrac{e^{1/x}(\tfrac{−1}{x^2})}{\left(\frac{−1}{x^2}\right)}=\lim_{x→∞}e^{1/x}=e^0=1. \nonumber \]
d. Lorsque le numérateur\(x→0,\) et le dénominateur s'approchent de zéro. Nous pouvons donc appliquer la règle de L'Hôpital. Nous obtenons
\[\lim_{x→0}\dfrac{\sin x−x}{x^2}=\lim_{x→0}\dfrac{\cos x−1}{2x}.\nonumber \]
Comme le numérateur et le dénominateur de ce nouveau quotient s'approchent tous deux de zéro\(x→0\), nous appliquons à nouveau la règle de L'Hôpital. Ce faisant, nous constatons que
\[\lim_{x→0}\dfrac{\cos x−1}{2x}=\lim_{x→0}\dfrac{−\sin x}{2}=0. \nonumber \]
Nous concluons donc que
\[\lim_{x→0}\dfrac{\sin x−x}{x^2}=0. \nonumber \]
Évaluer\[\lim_{x→0}\dfrac{x}{\tan x}. \nonumber \]
- Allusion
-
\(\dfrac{d}{dx}\big(\tan x\big)=\sec^2x\)
- Réponse
-
\(1\)
Nous pouvons également utiliser la règle de L'Hôpital pour évaluer les limites des quotients\(\dfrac{f(x)}{g(x)}\) dans lesquels\(f(x)→±∞\) et\(g(x)→±∞\). Les limites de cette forme sont classées comme des formes de type indéterminées\(∞/∞\). Encore une fois, notez que nous ne divisons pas réellement\(∞\) par\(∞\). Puisque ce n'\(∞\)est pas un nombre réel, c'est impossible ; il\(∞/∞\) est plutôt utilisé pour représenter un quotient de limites, chacune étant\(∞\) ou\(−∞\).
Supposons\(f\) et\(g\) sont des fonctions dérivables sur un intervalle ouvert contenant\(a\), sauf éventuellement, à\(a\). Supposons\(\displaystyle\lim_{x→a}f(x)=∞\) (ou\(−∞\)) et\(\displaystyle\lim_{x→a}g(x)=∞\) (ou\(−∞\)). Ensuite,
\[\lim_{x→a}\dfrac{f(x)}{g(x)}=\lim_{x→a}\dfrac{f′(x)}{g′(x)} \nonumber \]
en supposant que la limite du droit existe\(∞\) ou est\(−∞\). Ce résultat est également valable si la limite est infinie, si\(a=∞\) ou\(−∞\) si la limite est unilatérale.
Évaluez chacune des limites suivantes en appliquant la règle de L'Hôpital.
- \(\displaystyle\lim_{x→\infty}\dfrac{3x+5}{2x+1}\)
- \(\displaystyle \lim_{x→0^+}\dfrac{\ln x}{\cot x}\)
Solution
a. Depuis\(3x+5\) and \(2x+1\) are first-degree polynomials with positive leading coefficients, \(\displaystyle\lim_{x→∞}(3x+5)=∞\) and \(\displaystyle\lim_{x→∞}(2x+1)=∞\). Therefore, we apply L’Hôpital’s rule and obtain
\[\lim_{x→∞}\dfrac{3x+5}{2x+1}=\lim_{x→∞}\dfrac{3}{2}=\dfrac{3}{2}.\nonumber \]
Notez que cette limite peut également être calculée sans invoquer la règle de L'Hôpital. Plus tôt dans le chapitre, nous avons montré comment évaluer une telle limite en divisant le numérateur et le dénominateur par la plus grande puissance de x dans le dénominateur. Ce faisant, nous avons constaté que
\[\lim_{x→∞}\dfrac{3x+5}{2x+1}=\lim_{x→∞}\dfrac{3+5/x}{2+1/x}=\dfrac{3}{2}. \nonumber \]
La règle de L'Hôpital nous fournit un moyen alternatif d'évaluer ce type de limite.
b. Ici,\(\displaystyle \lim_{x→0^+}\ln x=−∞\) et\(\displaystyle \lim_{x→0^+}\cot x=∞\). Par conséquent, nous pouvons appliquer la règle de L'Hôpital et obtenir
\[\lim_{x→0^+}\dfrac{\ln x}{\cot x}=\lim_{x→0^+}\dfrac{1/x}{−\csc^2x}=\lim_{x→0^+}\dfrac{1}{−x \csc^2x}. \nonumber \]
Maintenant en tant que\(x→0^+, \csc^2x→∞\). Therefore, the first term in the denominator is approaching zero and the second term is getting really large. In such a case, anything can happen with the product. Therefore, we cannot make any conclusion yet. To evaluate the limit, we use the definition of \(\csc x\) to write
\[\lim_{x→0^+}\dfrac{1}{−x \csc^2x}=\lim_{x→0^+}\dfrac{\sin^2x}{−x}. \nonumber \]
Maintenant\(\displaystyle\lim_{x→0^+}\sin^2x=0\) and \(\displaystyle\lim_{x→0^+}-x=0\), so we apply L’Hôpital’s rule again. We find
\[\lim_{x→0^+}\dfrac{\sin^2x}{−x}=\lim_{x→0^+}\dfrac{2\sin x\cos x}{−1}=\dfrac{0}{−1}=0. \nonumber \]
Nous concluons que
\[\lim_{x→0^+}\dfrac{\ln x}{\cot x}=0. \nonumber \]
Évaluer\[\lim_{x→∞}\dfrac{\ln x}{5x}. \nonumber \]
- Allusion
-
\(\dfrac{d}{dx}\big(\ln x\big)=\dfrac{1}{x}\)
- Réponse
-
\(0\)
Comme nous l'avons mentionné, la règle de L'Hôpital est un outil extrêmement utile pour évaluer les limites. Il est toutefois important de se rappeler que pour appliquer la règle de L'Hôpital à un quotient\(\dfrac{f(x)}{g(x)}\), it is essential that the limit of \(\dfrac{f(x)}{g(x)}\) be of the form \(\dfrac{0}{0}\) or \(∞/∞\). Consider the following example.
Considérez\(\displaystyle\lim_{x→1}\dfrac{x^2+5}{3x+4}.\)
Démontrez que la limite ne peut pas être évaluée en appliquant la règle de L'Hôpital.
Solution
Comme les limites du numérateur et du dénominateur ne sont pas toutes deux nulles et ne sont pas toutes deux infinies, nous ne pouvons pas appliquer la règle de L'Hôpital. Si nous essayons de le faire, nous obtenons
\[\dfrac{d}{dx}(x^2+5)=2x\nonumber \]
et
\[\dfrac{d}{dx}(3x+4)=3. \nonumber \]
À ce stade, nous concluons à tort que
\[\lim_{x→1}\dfrac{x^2+5}{3x+4}=\lim_{x→1}\dfrac{2x}{3}=\dfrac{2}{3}. \nonumber \]
Cependant, depuis\(\displaystyle \lim_{x→1}(x^2+5)=6\) et\(\displaystyle \lim_{x→1}(3x+4)=7,\) nous avons
\[\lim_{x→1}\dfrac{x^2+5}{3x+4}=\dfrac{6}{7}. \nonumber \]
Nous pouvons en conclure que
\[\lim_{x→1}\dfrac{x^2+5}{3x+4}≠\lim_{x→1}\dfrac{\dfrac{d}{dx}(x^2+5)}{\dfrac{d}{dx}(3x+4).} \nonumber \]
Expliquez pourquoi nous ne pouvons pas appliquer la règle de L'Hôpital pour évaluer\(\displaystyle\lim_{x→0^+}\dfrac{\cos x}{x}\). Évaluez\(\displaystyle\lim_{x→0^+}\dfrac{\cos x}{x}\) par d'autres moyens.
- Allusion
-
Déterminez séparément les limites du numérateur et du dénominateur.
- Réponse
-
\(\displaystyle\lim_{x→0^+}\cos x=1.\)Nous ne pouvons donc pas appliquer la règle de L'Hôpital. La limite du quotient est\(∞.\)
Autres formes de nomination indéterminée
La règle de L'Hôpital est très utile pour évaluer les limites impliquant les formes indéterminées\(\dfrac{0}{0}\) et\(∞/∞\). Cependant, nous pouvons également utiliser la règle de L'Hôpital pour aider à évaluer les limites impliquant d'autres formes indéterminées qui apparaissent lors de l'évaluation des limites. Les expressions\(0⋅∞, ∞−∞, 1^∞, ∞^0\), et\(0^0\) sont toutes considérées comme des formes indéterminées. Ces expressions ne sont pas des nombres réels. Ils représentent plutôt des formes qui apparaissent lorsque l'on essaie d'évaluer certaines limites. Ensuite, nous comprenons pourquoi il s'agit de formulaires indéterminés, puis nous comprenons comment utiliser la règle de L'Hôpital dans ces cas. L'idée clé est que nous devons réécrire les formes indéterminées de telle sorte que nous arrivions à la forme indéterminée\(\dfrac{0}{0}\) ou\(∞/∞\).
Forme indéterminée de type 0⋅∞
Supposons que nous\(\displaystyle \lim_{x→a}(f(x)⋅g(x))\) souhaitions évaluer où\(f(x)→0\) et\(g(x)→∞\) (ou\(−∞\)) comme\(x→a\). Comme un terme du produit approche de zéro alors que l'autre devient arbitrairement grand (en amplitude), tout peut arriver au produit. Nous utilisons la notation\(0⋅∞\) pour indiquer la forme qui se présente dans cette situation. L'expression\(0⋅∞\) est considérée comme indéterminée car nous ne pouvons pas déterminer sans une analyse plus approfondie le comportement exact du produit\(f(x)g(x)\) en tant que\(x→∞\). Par exemple,\(n\) soit un entier positif et considérez
\(f(x)=\dfrac{1}{(x^n+1)}\)et\(g(x)=3x^2\).
Comme\(x→∞, f(x)→0\) et\(g(x)→∞\). Cependant, la limite\(f(x)g(x)=\dfrac{3x^2}{(x^n+1)}\) varie en fonction de\(n\).\(x→∞\) Si\(n=2\), alors\(\displaystyle\lim_{x→∞}f(x)g(x)=3\). Si\(n=1\), alors\(\displaystyle\lim_{x→∞}f(x)g(x)=∞\). Si\(n=3\), alors\(\displaystyle\lim_{x→∞}f(x)g(x)=0\). Nous examinons ici une autre limite impliquant la forme indéterminée\(0⋅∞\) et montrons comment réécrire la fonction sous forme de quotient pour utiliser la règle de L'Hôpital.
Évaluer\(\displaystyle \lim_{x→0^+}x\ln x.\)
Solution
Tout d'abord, réécrivez la fonction\(x\ln x\) sous forme de quotient pour appliquer la règle de L'Hôpital. Si nous écrivons
\[x\ln x=\dfrac{\ln x}{1/x} \nonumber \]
nous voyons cela au\(\ln x→−∞\) fur\(x→0^+\) et à\(\dfrac{1}{x}→∞\) mesure\(x→0^+\). Par conséquent, nous pouvons appliquer la règle de L'Hôpital et obtenir
\[\lim_{x→0^+}\dfrac{\ln x}{1/x}=\lim_{x→0^+}\dfrac{\dfrac{d}{dx}\big(\ln x\big)}{\dfrac{d}{dx}\big(1/x\big)}=\lim_{x→0^+}\dfrac{1/x}{−1/x^2}=\lim_{x→0^+}(−x)=0. \nonumber \]
Nous concluons que
\[\lim_{x→0^+}x\ln x=0. \nonumber \]
Évaluer\[\lim_{x→0}x\cot x. \nonumber \]
- Allusion
-
Écrire\(x\cot x=\dfrac{x \cos x}{\sin x}\)
- Réponse
-
\(1\)
Forme de type indéterminée\(∞−∞\)
Un autre type de formulaire indéterminé\(∞−∞.\) est l'exemple suivant. \(n\)Soit un entier positif et soit\(g(x)=3x^2+5\).\(f(x)=3x^n\) Comme\(x→∞, f(x)→∞\) et\(g(x)→∞\). Nous sommes intéressés par\(\displaystyle\lim_{x→∞}(f(x)−g(x))\). Selon qu'ils\(f(x)\) croissent plus vite,\(g(x)\) qu'ils croissent plus vite ou qu'ils croissent au même rythme, comme nous le verrons ensuite, tout peut se passer dans cette limite. Depuis\(f(x)→∞\) et\(g(x)→∞\), nous écrivons\(∞−∞\) pour indiquer la forme de cette limite. Comme c'est le cas pour nos autres formes indéterminées, elle n'\(∞−∞\)a aucune signification en soi et nous devons effectuer une analyse plus approfondie pour déterminer la valeur de la limite. Par exemple, supposons que l'exposant n de la fonction\(f(x)=3x^n\) est\(n=3\), alors
\[\lim_{x→∞}(f(x)−g(x))=\lim_{x→∞}(3x^3−3x^2−5)=∞. \nonumber \]
D'un autre côté, si c'est le\(n=2,\) cas
\[\lim_{x→∞}(f(x)−g(x))=\lim_{x→∞}(3x^2−3x^2−5)=−5. \nonumber \]
Cependant, si\(n=1\), alors
\[\lim_{x→∞}(f(x)−g(x))=\lim_{x→∞}(3x−3x^2−5)=−∞. \nonumber \]
Par conséquent, la limite ne peut pas être déterminée uniquement en prenant en compte\(∞−∞\). Nous verrons ensuite comment réécrire une expression impliquant la forme indéterminée\(∞−∞\) sous forme de fraction pour appliquer la règle de L'Hôpital.
Évaluer\[\lim_{x→0^+}\left(\dfrac{1}{x^2}−\dfrac{1}{\tan x}\right). \nonumber \]
Solution
En combinant les fractions, nous pouvons écrire la fonction sous forme de quotient. Puisque le plus petit dénominateur commun est\(x^2\tan x,\) que nous avons
\(\dfrac{1}{x^2}−\dfrac{1}{\tan x}=\dfrac{(\tan x)−x^2}{x^2\tan x}\).
\(x→0^+\)En tant que numérateur\(\tan x−x^2→0\) et dénominateur Nous pouvons\(x^2\tan x→0.\) donc appliquer la règle de L'Hôpital. En prenant les dérivées du numérateur et du dénominateur, nous avons
\[\lim_{x→0^+}\dfrac{(\tan x)−x^2}{x^2\tan x}=\lim_{x→0^+}\dfrac{(\sec^2x)−2x}{x^2\sec^2x+2x\tan x}. \nonumber \]
Comme\(x→0^+\),\((\sec^2x)−2x→1\) et\(x^2\sec^2x+2x\tan x→0\). Puisque le dénominateur est positif lorsqu'il s'\(x\)approche de zéro depuis la droite, nous concluons que
\[\lim_{x→0^+}\dfrac{(\sec^2x)−2x}{x^2\sec^2x+2x\tan x}=∞. \nonumber \]
Par conséquent,
\[\lim_{x→0^+}\left(\dfrac{1}{x^2}−\dfrac{1}{\tan x}\right)=∞. \nonumber \]
Évaluer\(\displaystyle \lim_{x→0^+}\left(\dfrac{1}{x}−\dfrac{1}{\sin x}\right)\).
- Allusion
-
Réécrivez la différence de fractions sous la forme d'une fraction unique.
- Réponse
-
0
Un autre type de forme indéterminée qui apparaît lors de l'évaluation des limites concerne les exposants. Les expressions\(0^0, ∞^0\), et\(1^∞\) sont toutes des formes indéterminées. À elles seules, ces expressions n'ont aucun sens car nous ne pouvons pas réellement les évaluer comme nous évaluerions une expression impliquant des nombres réels. Ces expressions représentent plutôt des formes qui apparaissent lors de la recherche de limites. Nous examinons maintenant comment la règle de L'Hôpital peut être utilisée pour évaluer les limites concernant ces formes indéterminées.
Comme la règle de L'Hôpital s'applique aux quotients, nous utilisons la fonction du logarithme naturel et ses propriétés pour réduire un problème évaluant une limite impliquant des exposants à un problème connexe impliquant une limite d'un quotient. Supposons, par exemple, que nous souhaitions évaluer\(\displaystyle \lim_{x→a}f(x)^{g(x)}\) et que nous arrivions à la forme indéterminée\(∞^0\). (Les formulaires\(0^0\) indéterminés\(1^∞\) peuvent être traités de la même manière.) Nous procédons comme suit. Laissez
\[y=f(x)^{g(x)}. \nonumber \]
Ensuite,
\[\ln y=\ln(f(x)^{g(x)})=g(x)\ln(f(x)). \nonumber \]
Par conséquent,
\[\lim_{x→a}[\ln(y)]=\lim_{x→a}[g(x)\ln(f(x))]. \nonumber \]
Puisque\(\displaystyle \lim_{x→a}f(x)=∞,\) nous le savons\(\displaystyle \lim_{x→a}\ln(f(x))=∞\). Par conséquent,\(\displaystyle \lim_{x→a}g(x)\ln(f(x))\) est de forme indéterminée\(0⋅∞\), et nous pouvons utiliser les techniques décrites précédemment pour réécrire l'expression\(g(x)\ln(f(x))\) sous une forme afin que nous puissions appliquer la règle de L'Hôpital. Supposons\(\displaystyle \lim_{x→a}g(x)\ln(f(x))=L\), où\(L\) se trouve\(∞\) ou\(−∞.\) alors
\[\lim_{x→a}[\ln(y)]=L. \nonumber \]
Comme la fonction logarithmique naturelle est continue, nous concluons que
\[\ln\left(\lim_{x→a}y\right)=L, \nonumber \]
ce qui nous donne
\[\lim_{x→a}y=\lim_{x→a}f(x)^{g(x)}=e^L. \nonumber \]
Évaluer\[\lim_{x→∞}x^{1/x}. \nonumber \]
Solution
\(y=x^{1/x}\)Laisse. Ensuite,
\[\ln(x^{1/x})=\dfrac{1}{x}\ln x=\dfrac{\ln x}{x}. \nonumber \]
Nous devons évaluer\(\displaystyle \lim_{x→∞}\dfrac{\ln x}{x}\). En appliquant la règle de L'Hôpital, nous obtenons
\[\lim_{x→∞}\ln y=\lim_{x→∞}\dfrac{\ln x}{x}=\lim_{x→∞}\dfrac{1/x}{1}=0. \nonumber \]
Par conséquent,\(\displaystyle \lim_{x→∞}\ln y=0.\) étant donné que la fonction logarithmique naturelle est continue, nous concluons que
\[\ln\left(\lim_{x→∞}y\right)=0, \nonumber \]
ce qui conduit à
\[\lim_{x→∞}x^{1/x}=\lim_{x→∞}y=e^{\ln\left(\lim_{x→∞}y\right)}=e^0=1. \nonumber \]
Par conséquent,
\[\lim_{x→∞}x^{1/x}=1. \nonumber \]
Évaluer\[\lim_{x→∞}x^{1/\ln(x)}. \nonumber \]
- Allusion
-
Supposons\(y=x^{1/\ln(x)}\) et appliquez le logarithme naturel aux deux côtés de l'équation.
- Réponse
-
\(e\)
Évaluer\[\lim_{x→0^+}x^{\sin x}. \nonumber \]
Solution
Laissez
\[y=x^{\sin x}. \nonumber \]
Par conséquent,
\[\ln y=\ln(x^{\sin x})=\sin x\ln x. \nonumber \]
Nous évaluons maintenant\(\displaystyle\lim_{x→0^+}\sin x\ln x.\)\(\displaystyle\lim_{x→0^+}\sin x=0\)\(\displaystyle\lim_{x→0^+}\ln x=−∞\) Since et, nous avons la forme indéterminée\(0⋅∞\). Pour appliquer la règle de L'Hôpital, nous devons la réécrire\(\sin x\ln x\) en fraction. Nous pourrions écrire
\[\sin x\ln x=\dfrac{\sin x}{1/\ln x} \nonumber \]
ou
\[\sin x\ln x=\dfrac{\ln x}{1/\sin x}=\dfrac{\ln x}{\csc x}. \nonumber \]
Considérons la première option. Dans ce cas, en appliquant la règle de L'Hôpital, nous obtiendrions
\[\lim_{x→0^+}\sin x\ln x=\lim_{x→0^+}\dfrac{\sin x}{1/\ln x}=\lim_{x→0^+}\dfrac{\cos x}{−1/(x(\ln x)^2)}=\lim_{x→0^+}(−x(\ln x)^2\cos x).\nonumber \]
Malheureusement, nous avons non seulement une autre expression impliquant la forme indéterminée,\(0⋅∞,\) mais la nouvelle limite est encore plus compliquée à évaluer que celle avec laquelle nous avons commencé. Au lieu de cela, nous essayons la deuxième option. En écrivant
\[\sin x\ln x=\dfrac{\ln x}{1/\sin x}=\dfrac{\ln x}{\csc x,} \nonumber \]
et en appliquant la règle de L'Hôpital, nous obtenons
\[\lim_{x→0^+}\sin x\ln x=\lim_{x→0^+}\dfrac{\ln x}{\csc x}=\lim_{x→0^+}\dfrac{1/x}{−\csc x\cot x}=\lim_{x→0^+}\dfrac{−1}{x\csc x\cot x}. \nonumber \]
En utilisant le fait que\(\csc x=\dfrac{1}{\sin x}\) et\(\cot x=\dfrac{\cos x}{\sin x}\), nous pouvons réécrire l'expression sur le côté droit comme
\[\lim_{x→0^+}\dfrac{−\sin^2x}{x\cos x}=\lim_{x→0^+}\left[\dfrac{\sin x}{x}⋅(−\tan x)\right]=\left(\lim_{x→0^+}\dfrac{\sin x}{x}\right)⋅\left(\lim_{x→0^+}(−\tan x)\right)=1⋅0=0. \nonumber \]
Nous concluons que,\(\displaystyle\lim_{x→0^+}\ln y=0.\) par conséquent,\(\displaystyle\ln\left(\lim_{x→0^+}y\right)=0\) et nous avons
\[\lim_{x→0^+}y=\lim_{x→0^+}x^{\sin x}=e^0=1.\nonumber \]
Par conséquent,
\[\lim_{x→0^+}x^{\sin x}=1. \nonumber \]
Évaluer\(\displaystyle \lim_{x→0^+}x^x\).
- Allusion
-
Supposons\(y=x^x\) le logarithme naturel des deux côtés de l'équation.
- Réponse
-
1
Taux de croissance des fonctions
Supposons que\(f\)\(g\) les fonctions s'approchent de l'infini comme\(x→∞\). Bien que les valeurs des deux fonctions deviennent arbitrairement élevées au fur et à mesure que les valeurs de\(x\) deviennent suffisamment grandes, l'une des fonctions croît parfois plus rapidement que l'autre. Par exemple,\(f(x)=x^2\) et\(g(x)=x^3\) les deux s'approchent de l'infini comme\(x→∞\). Cependant, comme le\(\PageIndex{1}\) montre le tableau, les valeurs de\(x^3\) augmentent beaucoup plus rapidement que les valeurs de\(x^2\).
| \(x\) | 10 | 100 | 1000 | 10 000 |
|---|---|---|---|---|
| \(f(x)=x^2\) | 100 | 10 000 | 1 000 000 | 100 000 000 |
| \(g(x)=x^3\) | 1000 | 1 000 000 | 1 000 000 000 | 1 000 000 000 000 |
En fait,
\[\lim_{x→∞}\dfrac{x^3}{x^2}=\lim_{x→∞}x=∞. \nonumber \]
ou, de manière équivalente
\[\lim_{x→∞}\dfrac{x^2}{x^3}=\lim_{x→∞}\dfrac{1}{x}=0. \nonumber \]
En conséquence, nous disons qu'\(x^3\)il croît plus rapidement que\(x^2\) tel\(x→∞\). D'autre part, pour\(f(x)=x^2\) et\(g(x)=3x^2+4x+1\), bien que les valeurs de\(g(x)\) soient toujours supérieures aux valeurs de\(f(x)\) for\(x>0\), chaque valeur de\(g(x)\) est environ trois fois la valeur correspondante de\(f(x)\) as\(x→∞\), comme indiqué dans le tableau\(\PageIndex{2}\). En fait,
\[\lim_{x→∞}\dfrac{x^2}{3x^2+4x+1}=\dfrac{1}{3}. \nonumber \]
| \(x\) | 10 | 100 | 1000 | 10 000 |
|---|---|---|---|---|
| \(f(x)=x^2\) | 100 | 10 000 | 1 000 000 | 100 000 000 |
| \(g(x)=3x^2+4x+1\) | 341 | 30 401 | 3 004 001 | 300 040 001 |
Dans ce cas, nous disons cela\(x^2\) et\(3x^2+4x+1\) nous progressons au même rythme que\(x→∞.\)
Plus généralement, supposons\(f\) et\(g\) sont deux fonctions qui s'approchent de l'infini comme\(x→∞\). Nous disons qu'\(g\)elle croît plus rapidement que\(f\) comme\(x→∞\) si
\[\lim_{x→∞}\dfrac{g(x)}{f(x)}=∞ \quad \text{or, equivalently,} \quad \lim_{x→∞}\dfrac{f(x)}{g(x)}=0. \nonumber \]
En revanche, s'il existe une constante\(M≠0\) telle que
\[\lim_{x→∞}\dfrac{f(x)}{g(x)}=M, \nonumber \]
nous disons\(f\) et\(g\) croissons au même rythme que\(x→∞\).
Nous verrons ensuite comment utiliser la règle de L'Hôpital pour comparer les taux de croissance des fonctions de puissance, exponentielles et logarithmiques.
Pour chacune des paires de fonctions suivantes, utilisez la règle de L'Hôpital pour évaluer\[\lim_{x→∞}\dfrac{f(x)}{g(x)}. \nonumber \]
- \(f(x)=x^2\)et\(g(x)=e^x\)
- \(f(x)=\ln(x)\)et\(g(x)=x^2\)
Solution
a. Depuis\(\displaystyle \lim_{x→∞}x^2=∞\) et\(\displaystyle \lim_{x→∞}e^x=∞\), nous pouvons utiliser la règle de L'Hôpital pour évaluer\(\displaystyle \lim_{x→∞}\left[\dfrac{x^2}{e^x}\right]\). Nous obtenons
\[\lim_{x→∞}\frac{x^2}{e^x}=\lim_{x→∞}\frac{2x}{e^x}. \nonumber \]
Depuis\(\displaystyle \lim_{x→∞}2x=∞\)\(\displaystyle \lim_{x→∞}e^x=∞\), nous pouvons à nouveau appliquer la règle de L'Hôpital. Depuis
\[\lim_{x→∞}\frac{2x}{e^x}=\lim_{x→∞}\frac{2}{e^x}=0, \nonumber \]
nous concluons que
\[\lim_{x→∞}\dfrac{x^2}{e^x}=0. \nonumber \]
Par conséquent,\(e^x\) croît plus rapidement qu'au\(x^2\) fur et à mesure\(x→∞\) (voir figure\(\PageIndex{3}\) et tableau\(\PageIndex{3}\))
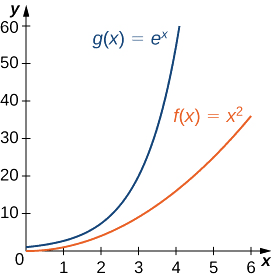
| \(x\) | 5 | 10 | 15 | 20 |
|---|---|---|---|---|
| \(x^2\) | 25 | 100 | 225 | 400 |
| \(e^x\) | 148 | 22 026 | 3 269 017 | 485 165 195 |
b. Depuis\(\displaystyle \lim_{x→∞}\ln x=∞\) et\(\displaystyle \lim_{x→∞}x^2=∞\), nous pouvons utiliser la règle de L'Hôpital pour évaluer\(\displaystyle \lim_{x→∞}\dfrac{\ln x}{x^2}\). Nous obtenons
\[\lim_{x→∞}\dfrac{\ln x}{x^2}=\lim_{x→∞}\dfrac{1/x}{2x}=\lim_{x→∞}\dfrac{1}{2x^2}=0. \nonumber \]
Il\(x^2\) croît donc plus rapidement qu'au\(\ln x\) fur et à mesure\(x→∞\) (voir Figure\(\PageIndex{4}\) et Tableau\(\PageIndex{4}\)).
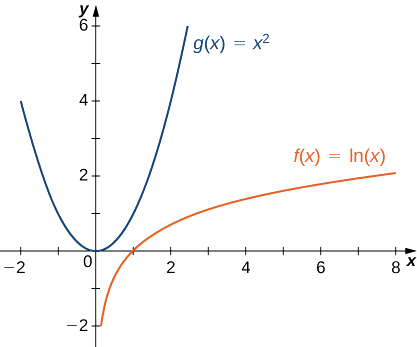
| \(x\) | 10 | 100 | 1000 | 10 000 |
|---|---|---|---|---|
| \(\ln(x)\) | 2.303 | 4.605 | 6 908 | 9,210 |
| \(x^2\) | 100 | 10 000 | 1 000 000 | 100 000 000 |
Comparez les taux de croissance de\(x^{100}\) et\(2^x\).
- Allusion
-
Appliquez la règle de L'Hôpital à\(x^{100}/2^x\).
- Réponse
-
La fonction\(2^x\) se développe plus rapidement que\(x^{100}\).
En utilisant les mêmes idées que dans l'exemple\(\PageIndex{8}a\). Il n'est pas difficile de montrer qu'elle\(e^x\) croît plus rapidement que\(x^p\) pour n'importe quelle autre\(p>0\). Dans la figure\(\PageIndex{5}\) et le tableau\(\PageIndex{5}\), nous comparons\(e^x\) avec\(x^3\) et\(x^4\) comme\(x→∞\).
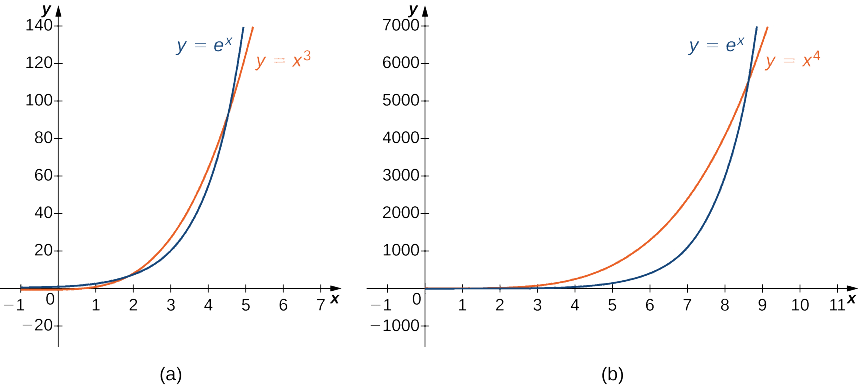
| \(x\) | 5 | 10 | 15 | 20 |
|---|---|---|---|---|
| \(x^3\) | 125 | 1000 | 375 | 8000 |
| \(x^4\) | 625 | 10 000 | 50 625 | 160 000 |
| \(e^x\) | 148 | 22 026 | 3 269 017 | 485 165 195 |
De même, il n'est pas difficile de montrer qu'elle\(x^p\) croît plus rapidement que\(\ln x\) pour n'importe quelle autre\(p>0\). Dans la figure\(\PageIndex{6}\) et le tableau\(\PageIndex{6}\), nous comparons\(\ln x\) avec\(\sqrt[3]{x}\) et\(\sqrt{x}\).
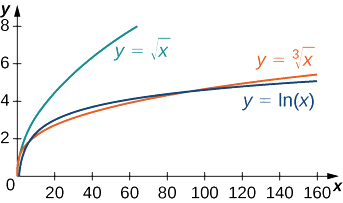
| \(x\) | 10 | 100 | 1000 | 10 000 |
|---|---|---|---|---|
| \(\ln(x)\) | 2.303 | 4.605 | 6 908 | 9,210 |
| \(\sqrt[3]{x}\) | 2.154 | 4 642 | 10 | 21 544 |
| \(\sqrt{x}\) | 3.162 | 10 | 31 623 | 100 |
Concepts clés
- La règle de L'Hôpital peut être utilisée pour évaluer la limite d'un quotient lorsque la forme\(\dfrac{0}{0}\) indéterminée\(∞/∞\) apparaît.
- La règle de L'Hôpital peut également être appliquée à d'autres formes indéterminées si elles peuvent être réécrites en termes de limite impliquant un quotient de forme indéterminée\(\dfrac{0}{0}\) ou\(∞/∞.\)
- La fonction exponentielle\(e^x\) croît plus rapidement que n'importe quelle fonction de puissance\(x^p, p>0\).
- La fonction logarithmique\(\ln x\) croît plus lentement que n'importe quelle fonction de puissance\(x^p, p>0\).
Lexique
- formes indéterminées
- Lors de l'évaluation d'une limite\(\dfrac{0}{0}\), les formes\(∞/∞, 0⋅∞, ∞−∞, 0^0, ∞^0\), et\(1^∞\) sont considérées comme indéterminées car une analyse plus approfondie est nécessaire pour déterminer si la limite existe et, dans l'affirmative, quelle est sa valeur.
- La règle de L'Hôpital
- Si\(f\) et\(g\) sont des fonctions dérivables sur un intervalle\(a\), sauf éventuellement à\(a\),\(\displaystyle \lim_{x→a}f(x)=0=\lim_{x→a}g(x)\) et/ou\(\displaystyle \lim_{x→a}f(x)\) et\(\displaystyle \lim_{x→a}g(x)\) sont infinies, alors\(\displaystyle \lim_{x→a}\dfrac{f(x)}{g(x)}=\lim_{x→a}\dfrac{f′(x)}{g′(x)}\), en supposant que la limite à droite existe ou est\(∞\) ou\(−∞\).


