4.7 : Problèmes d'optimisation appliquée

Last updated
Save as PDF

Page ID: 197580

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objectifs d'apprentissage

Configurez et résolvez des problèmes d'optimisation dans plusieurs domaines appliqués.

Une application courante du calcul consiste à calculer la valeur minimale ou maximale d'une fonction. Par exemple, les entreprises souhaitent souvent minimiser leurs coûts de production ou maximiser leurs revenus. Lors de la fabrication, il est souvent souhaitable de minimiser la quantité de matériau utilisée pour emballer un produit d'un certain volume. Dans cette section, nous montrons comment configurer ces types de problèmes de minimisation et de maximisation et les résoudre à l'aide des outils développés dans ce chapitre.

Résolution des problèmes d'optimisation sur un intervalle fermé et limité

L'idée de base des problèmes d'optimisation qui suivent est la même. Nous avons une quantité particulière que nous souhaitons maximiser ou minimiser. Cependant, nous avons également une condition auxiliaire qui doit être satisfaite. Par exemple, dans Exemple$\PageIndex{1}$, nous souhaitons maximiser la superficie d'un jardin rectangulaire. Il est certain que si nous continuons à agrandir les côtés du jardin, la superficie continuera de s'agrandir. Mais que se passerait-il si nous avions des restrictions quant à la quantité de clôtures que nous pouvons utiliser pour le périmètre ? Dans ce cas, nous ne pouvons pas agrandir le jardin à notre guise. Voyons comment nous pouvons maximiser la surface d'un rectangle sous réserve de certaines contraintes sur le périmètre.

Exemple$\PageIndex{1}$: Maximizing the Area of a Garden

Un jardin rectangulaire doit être construit en utilisant une paroi rocheuse comme côté du jardin et des clôtures grillagées pour les trois autres côtés (Figure$\PageIndex{1}$). Étant donné$100\,\text{ft}$ les clôtures grillagées, déterminez les dimensions qui créeraient un jardin de superficie maximale. Quelle est la surface maximale ?

Un dessin d'un jardin comporte des lettres x et y sur les côtés verticaux et horizontaux, respectivement. Une paroi rocheuse s'étend sur toute la longueur horizontale inférieure du dessin. — Figure$\PageIndex{1}$ : Nous voulons déterminer les mesures$x$ et$y$ créer un jardin avec une superficie maximale en utilisant$100\,\text{ft}$ des clôtures.

Solution

$x$Soit la longueur du côté du jardin perpendiculaire à la paroi rocheuse et$y$ la longueur du côté parallèle à la paroi rocheuse. Ensuite, la superficie du jardin est

$A=x⋅y.$

Nous voulons trouver la surface maximale possible sous réserve de la contrainte de la clôture totale$100\,\text{ft}$. À partir de la figure$\PageIndex{1}$, la quantité totale de clôtures utilisées sera$2x+y.$ Par conséquent, l'équation de contrainte est

$2x+y=100.$

En résolvant cette équation pour$y$, nous avons$y=100−2x.$ Ainsi, nous pouvons écrire la zone comme

$A(x)=x⋅(100−2x)=100x−2x^2.$

Avant d'essayer de maximiser la fonction de zone,$A(x)=100x−2x^2,$ nous devons déterminer le domaine considéré. Pour construire un jardin rectangulaire, il faut certainement que les longueurs des deux côtés soient positives. Par conséquent, nous avons besoin$x>0$ et$y>0$. Depuis$y=100−2x$, si$y>0$, alors$x<50$. Par conséquent, nous essayons de déterminer la valeur maximale de$A(x)$ pour$x$ sur l'intervalle ouvert$(0,50)$. Nous ne savons pas si une fonction a nécessairement une valeur maximale sur un intervalle ouvert. Cependant, nous savons qu'une fonction continue a un maximum absolu (et un minimum absolu) sur un intervalle fermé. Par conséquent, considérons la fonction$A(x)=100x−2x^2$ sur l'intervalle fermé$[0,50]$. Si la valeur maximale se trouve à un point intérieur, nous avons trouvé la valeur$x$ dans l'intervalle ouvert$(0,50)$ qui maximise la surface du jardin.

Par conséquent, nous considérons le problème suivant :

Maximisez$A(x)=100x−2x^2$ au fil de l'intervalle$[0,50].$

Comme mentionné précédemment, étant donné qu'$A$il s'agit d'une fonction continue sur un intervalle fermé et borné, selon le théorème des valeurs extrêmes, elle a un maximum et un minimum. Ces valeurs extrêmes se produisent soit aux points finaux, soit aux points critiques. Aux points de terminaison,$A(x)=0$. Comme la zone est positive pour tous$x$ dans l'intervalle ouvert$(0,50)$, le maximum doit se produire à un point critique. En différenciant la fonction$A(x)$, nous obtenons

$A′(x)=100−4x.$

Par conséquent, le seul point critique est$x=25$ (Figure$\PageIndex{2}$). Nous concluons que la surface maximale doit se produire lorsque$x=25$.

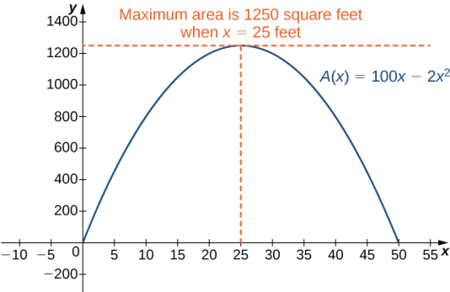
La fonction A (x) = 100x — 2x est représentée graphiquement. Au maximum, il y a une intersection de deux lignes pointillées et du texte qui se lit comme suit : « La superficie maximale est de 1 250 pieds carrés lorsque x = 25 pieds ». — Figure$\PageIndex{2}$ : Pour maximiser la superficie du jardin, nous devons trouver la valeur maximale de la fonction$A(x)=100x−2x^2$.

Ensuite, nous$y=100−2x=100−2(25)=50.$ devons maximiser la superficie du jardin, laisser$x=25\,\text{ft}$ et$y=50\,\text{ft}$. La superficie de ce jardin est de$1250\, \text{ft}^2$.

Exercice$\PageIndex{1}$

Déterminez la surface maximale si nous voulons créer le même jardin rectangulaire que sur la figure$\PageIndex{2}$, mais nous n'avons pas$200\,\text{ft}$ de clôtures.

Allusion: Nous devons maximiser la fonction$A(x)=200x−2x^2$ sur l'intervalle$[0,100].$

Réponse: La surface maximale est de$5000\, \text{ft}^2$.

Examinons maintenant une stratégie générale pour résoudre les problèmes d'optimisation, similaire à Example$\PageIndex{1}$.

Stratégie de résolution de problèmes : résolution des problèmes d'optimisation

Introduisez toutes les variables. Le cas échéant, dessinez une figure et étiquetez toutes les variables.
Déterminez quelle quantité doit être maximisée ou minimisée, et pour quelle plage de valeurs des autres variables (si cela peut être déterminé à ce stade).
Écrivez une formule pour la quantité à maximiser ou à minimiser en termes de variables. Cette formule peut impliquer plus d'une variable.
Écrivez toutes les équations reliant les variables indépendantes de la formule à partir de l'étape$3$. Utilisez ces équations pour écrire la quantité à maximiser ou à minimiser en fonction d'une variable.
Déterminez le domaine à prendre en compte pour la$4$ fonction étape par étape en fonction du problème physique à résoudre.
Localisez la valeur maximale ou minimale de la fonction à partir de l'étape$4.$ Cette étape implique généralement de rechercher des points critiques et d'évaluer une fonction aux extrémités.

Appliquons maintenant cette stratégie pour maximiser le volume d'une boîte à toit ouvert compte tenu de la quantité de matériau à utiliser.

Exemple$\PageIndex{2}$: Maximizing the Volume of a Box

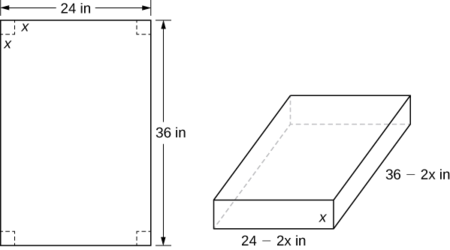
Une boîte à couvercle ouvert doit être fabriquée à partir d'un$24\,\text{in.}$$36\,\text{in.}$ morceau de carton en retirant un carré de chaque coin de la boîte et en repliant les rabats de chaque côté. Quelle taille de carré faut-il découper dans chaque coin pour obtenir une boîte avec le volume maximum ?

Solution

Étape 1 :$x$ Soit la longueur du côté du carré à retirer de chaque coin (Figure$\PageIndex{3}$). Ensuite, les quatre rabats restants peuvent être repliés pour former une boîte ouverte. $V$Soit le volume de la boîte résultante.

Ce chiffre comporte deux chiffres. Le premier est un rectangle dont les côtés sont de 24 pouces et 36 pouces, chaque coin ayant un carré de côté x retiré de celui-ci. Sur la deuxième photo, il y a une boîte avec des longueurs de côté de x pouces, 24 à 2 pouces et 36 à 2 pouces. — Figure$\PageIndex{3}$ : Un carré de$x$ pouces de côté est retiré de chaque coin de la feuille de carton. Les rabats restants sont pliés pour former une boîte ouverte.

Étape 2 : Nous essayons de maximiser le volume d'une boîte. Le problème est donc de maximiser$V$.

Étape 3 : Comme indiqué à l'étape 2, essayez de maximiser le volume d'une boîte. Le volume d'une boîte est

\[V=L⋅W⋅H \nonumber, \nonumber \]

où$L,\,W,$ et$H$ sont respectivement la longueur, la largeur et la hauteur.

Étape 4 : Sur la figure$\PageIndex{3}$, nous voyons que la hauteur de la boîte est$x$ en pouces, la longueur$36−2x$ en pouces et la largeur$24−2x$ en pouces. Par conséquent, le volume de la boîte est

\[ \begin{align*} V(x) &=(36−2x)(24−2x)x \\[4pt] &=4x^3−120x^2+864x \end{align*}. \nonumber \]

Étape 5 : Pour déterminer le domaine à prendre en compte, examinons la figure$\PageIndex{3}$. Bien sûr, nous$x>0.$ avons besoin de plus, la longueur du côté du carré ne peut pas être supérieure ou égale à la moitié de la longueur du côté le plus court,$24\,\text{in.}$ sinon l'un des rabats serait complètement coupé. Par conséquent, nous essayons de déterminer s'il existe un volume maximum de la boîte au-delà de l'intervalle ouvert.$(0,12).$ Comme il s'$V$agit d'une fonction continue sur l'intervalle fermé$[0,12]$, nous savons qu'elle$V$ aura un maximum absolu sur l'intervalle fermé.$x$ Par conséquent, nous examinons l'$V$intervalle fermé$[0,12]$ et vérifions si le maximum absolu se produit à un point intérieur.

Étape 6 : Puisque$V(x)$ est une fonction continue sur l'intervalle fermé et borné$[0,12]$,$V$ doit avoir un maximum absolu (et un minimum absolu). Car$V(x)=0$ aux extrémités et$V(x)>0$ pour$0<x<12,$ le maximum, il doit se produire à un point critique. Le dérivé est

$V′(x)=12x^2−240x+864.$

Pour trouver les points critiques, nous devons résoudre l'équation

$12x^2−240x+864=0.$

En divisant les deux côtés de cette équation par$12$, le problème simplifie la résolution de l'équation

$x^2−20x+72=0.$

En utilisant la formule quadratique, nous trouvons que les points critiques sont

\[\begin{align*} x &=\dfrac{20±\sqrt{(−20)^2−4(1)(72)}}{2} \\[4pt] &=\dfrac{20±\sqrt{112}}{2} \\[4pt] &=\dfrac{20±4\sqrt{7}}{2} \\[4pt] &=10±2\sqrt{7} \end{align*}. \nonumber \]

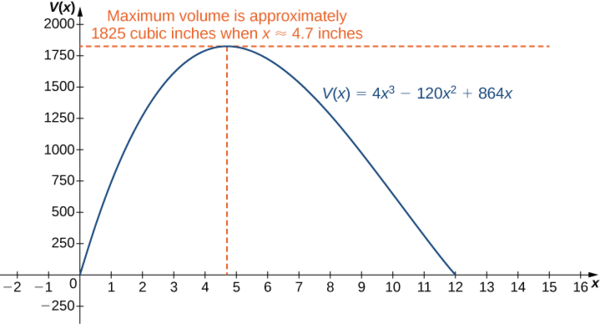
Comme cela$10+2\sqrt{7}$ n'entre pas dans le domaine de la prise en compte, le seul point critique que nous devons prendre en compte est$10−2\sqrt{7}$. Par conséquent, le volume est maximisé si nous laissons$x=10−2\sqrt{7}\,\text{in.}$ le volume maximum est

\[V(10−2\sqrt{7})=640+448\sqrt{7}≈1825\,\text{in}^3. \nonumber \]

comme le montre le graphique suivant.

La fonction V (x) = 4x3 — 120x2 + 864x est représentée graphiquement. À son maximum, il y a une intersection de deux lignes pointillées et du texte indiquant « Le volume maximum est d'environ 1 825 pouces cubes lorsque x ≈ 4,7 pouces ». — Figure$\PageIndex{4}$ : La maximisation du volume de la boîte permet de trouver la valeur maximale d'un polynôme cubique.

Exercice$\PageIndex{2}$

Supposons que les dimensions du carton dans l'exemple$\PageIndex{2}$ soient$20\,\text{in.}$ de$30\,\text{in.}$ Let$x$ be la longueur de côté de chaque carré et d'écrire le volume de la boîte ouverte en fonction de$x$. Déterminez le domaine à prendre en compte pour$x$.

Allusion: Le volume de la boîte est$L⋅W⋅H.$

Réponse: $V(x)=x(20−2x)(30−2x).$Le domaine est$[0,10]$.

Exemple$\PageIndex{3}$: Minimizing Travel Time

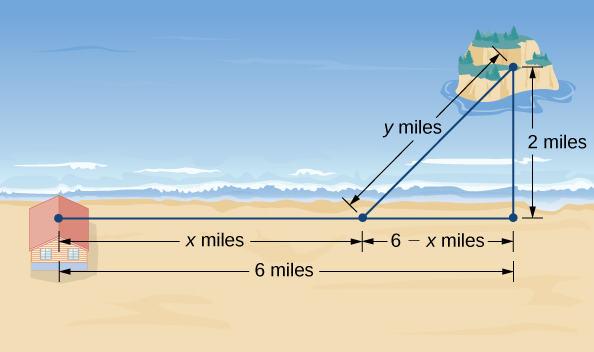
Une île se$2$ trouve à un kilomètre au nord de son point le plus proche, le long d'un rivage droit. Un visiteur séjourne dans une cabane sur le rivage, à un kilomètre$6$ à l'ouest de ce point. Le visiteur prévoit de se rendre de la cabane à l'île. Supposons que le visiteur court à une vitesse de$8$ mph et nage à une vitesse de$3$ mph. Jusqu'où le visiteur doit-il courir avant de se baigner afin de minimiser le temps nécessaire pour atteindre l'île ?

Solution

Étape 1 :$x$ Soit la distance parcourue et la distance parcourue$y$ à la nage (Figure$\PageIndex{5}$). Que$T$ soit le temps qu'il faut pour se rendre de la cabine à l'île.

La cabine se trouve à x miles du rivage. De ce point sur le rivage, l'île se trouve à des kilomètres. Si vous deviez poursuivre la ligne allant de la cabine au rivage (celle des x miles) et si vous deviez tracer une ligne depuis l'île parallèlement au rivage, les lignes s'étendraient sur 3 km depuis l'île et 10 km depuis la cabine avant de se croiser. — Figure$\PageIndex{5}$ : Comment choisir$x$ et$y$ minimiser le temps de trajet entre la cabine et l'île ?

Étape 2 : Le problème est de minimiser$T$.

Étape 3 : Pour trouver le temps passé à voyager de la cabine à l'île, ajoutez le temps passé à courir et le temps passé à nager. Puisque Distance = Taux × Temps,$(D=R×T),$ le temps passé à courir est

$T_{running}=\dfrac{D_{running}}{R_{running}}=\dfrac{x}{8}$,

et le temps passé à nager est

$T_{swimming}=\dfrac{D_{swimming}}{R_{swimming}}=\dfrac{y}{3}$.

Par conséquent, le temps total passé à voyager est

$T=\dfrac{x}{8}+\dfrac{y}{3}$.

Étape 4 : À partir de la figure$\PageIndex{5}$, le segment linéaire des$y$ miles forme l'hypoténuse d'un triangle droit avec des jambes de longueur$2$ mi et$6−x$ mi. Par conséquent, par le théorème de Pythagore$2^2+(6−x)^2=y^2$, et nous obtenons$y=\sqrt{(6−x)^2+4}$. Ainsi, le temps total passé à voyager est donné par la fonction

$T(x)=\dfrac{x}{8}+\dfrac{\sqrt{(6−x)^2+4}}{3}$.

Étape 5 : À partir de la figure$\PageIndex{5}$, nous voyons cela$0≤x≤6$. C'$[0,6]$est donc le domaine à prendre en compte.

Étape 6 : Comme$T(x)$ il s'agit d'une fonction continue sur un intervalle fermé et limité, elle a un maximum et un minimum. Commençons par rechercher les points critiques de l'$T$intervalle.$[0,6].$ La dérivée est

\[\begin{align*} T′(x) &=\dfrac{1}{8}−\dfrac{1}{2}\dfrac{[(6−x)^2+4]^{−1/2}}{3}⋅2(6−x) \\[4pt] &=\dfrac{1}{8}−\dfrac{(6−x)}{3\sqrt{(6−x)^2+4}} \end{align*}\]

Si$T′(x)=0,$, alors

\[\dfrac{1}{8}=\dfrac{6−x}{3\sqrt{(6−x)^2+4}} \label{ex3eq1} \]

Par conséquent,

\[3\sqrt{(6−x)^2+4}=8(6−x). \label{ex3eq2} \]

En mettant au carré les deux côtés de cette équation, nous voyons que si$x$ elle satisfait à cette équation, alors$x$ doit satisfaire

\[9[(6−x)^2+4]=64(6−x)^2,\nonumber \]

ce qui implique

\[55(6−x)^2=36. \nonumber \]

Nous concluons que$x$ c'est un point critique, alors$x$ satisfait

\[(x−6)^2=\dfrac{36}{55}. \nonumber \]

[Notez que puisque nous sommes en train de quadriller,$ (x-6)^2 = (6-x)^2.$]

Par conséquent, les possibilités pour les points critiques sont

\[x=6±\dfrac{6}{\sqrt{55}}.\nonumber \]

N'$x=6+6/\sqrt{55}$étant pas dans le domaine, il ne s'agit pas d'une possibilité pour un point critique. D'un autre côté,$x=6−6/\sqrt{55}$ c'est dans le domaine. Puisque nous avons quadrillé les deux côtés de l'équation \ ref {ex3eq2} pour arriver aux points critiques possibles, il reste à vérifier que l'équation$x=6−6/\sqrt{55}$ est conforme à l'équation \ ref {ex3eq1}. Comme$x=6−6/\sqrt{55}$ cela répond à cette équation, nous concluons qu'il$x=6−6/\sqrt{55}$ s'agit d'un point critique, et c'est le seul. Pour justifier que le temps est minimisé pour cette valeur de$x$, il suffit de vérifier les valeurs de$T(x)$ aux extrémités$x=0$ et$x=6$ de les comparer$T(x)$ à la valeur du point critique$x=6−6/\sqrt{55}$. Nous constatons que$T(0)≈2.108\,\text{h}$ et$T(6)≈1.417\,\text{h}$, alors que

\[T(6−6/\sqrt{55})≈1.368\,\text{h}. \nonumber \]

Par conséquent, nous concluons qu'il y$T$ a un minimum local à$x≈5.19$ mi.

Exercice$\PageIndex{3}$

Supposons que l'île$1$ se trouve à un kilomètre du rivage et que la distance entre la cabine et le point sur le rivage le plus proche de l'île est de$15$ miles. Supposons qu'un visiteur nage à une vitesse de$2.5$ mph et court à une vitesse de$6$ mph. Indiquez$x$ la distance que le visiteur parcourra avant de nager et déterminez le temps qu'il lui faudra pour se rendre de la cabine à l'île.

Allusion: L'heure$T=T_{running}+T_{swimming}.$

Réponse: $T(x)=\dfrac{x}{6}+\dfrac{\sqrt{(15−x)^2+1}}{2.5} $

En affaires, les entreprises souhaitent maximiser leurs revenus. Dans l'exemple suivant, nous examinons un scénario dans lequel une entreprise a collecté des données sur le nombre de voitures qu'elle est en mesure de louer, en fonction du prix qu'elle facture à ses clients pour louer une voiture. Utilisons ces données pour déterminer le prix que l'entreprise doit facturer afin de maximiser le montant d'argent qu'elle rapporte.

Exemple$\PageIndex{4}$: Maximizing Revenue

Les propriétaires d'une société de location de voitures ont déterminé que s'ils facturent des$p$ dollars par jour à leurs clients pour louer une voiture$50≤p≤200$, le nombre de voitures$n$ qu'ils louent par jour peut être modélisé par la fonction linéaire$n(p)=1000−5p$. S'ils facturent$$50$ par jour ou moins, ils loueront toutes leurs voitures. S'ils facturent$$200$ par jour ou plus, ils ne loueront pas de voitures. En supposant que les propriétaires prévoient de facturer leurs clients entre une fois$$50$ par$$200$ jour et par jour pour la location d'une voiture, quel montant devraient-ils facturer pour maximiser leurs revenus ?

Solution

Étape 1 :$p$ Soit le prix facturé par voiture et par jour et$n$ soit le nombre de voitures louées par jour. $R$Soyons le revenu par jour.

Étape 2 : Le problème est de maximiser$R.$

Étape 3 : Le revenu (par jour) est égal au nombre de voitures louées par jour multiplié par le prix facturé par voiture et par jour, c'est-à-dire$R=n×p.$

Étape 4 : Comme le nombre de voitures louées par jour est modélisé par la fonction linéaire,$n(p)=1000−5p,$ les revenus$R$ peuvent être représentés par la fonction

\[ \begin{align*} R(p) &=n×p \\[4pt] &=(1000−5p)p \\[4pt] &=−5p^2+1000p.\end{align*}\]

Étape 5 : Étant donné que les propriétaires prévoient de facturer entre$$50$ par voiture par jour et$$200$ par voiture et par jour, le problème est de trouver le revenu maximum$R(p)$ pour$p$ un intervalle fermé$[50,200]$.

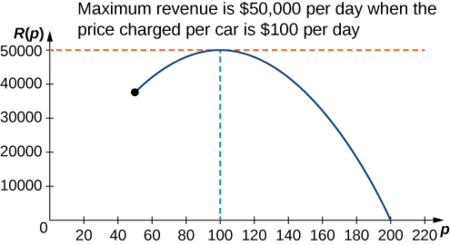
Étape 6 : Comme il$R$ s'agit d'une fonction continue sur l'intervalle fermé et limité$[50,200]$, elle a un maximum absolu (et un minimum absolu) dans cet intervalle. Pour trouver la valeur maximale, recherchez les points critiques. La dérivée est$R′(p)=−10p+1000.$ donc, le point critique est$p=100$. Quand,$p=100, R(100)=$50,000.$ quand$p=50, R(p)=$37,500$. Quand$p=200, R(p)=$0$.

Par conséquent, le maximum absolu se situe à$p=$100$. La société de location de voitures doit facturer$$100$ par jour et par voiture afin de maximiser ses revenus, comme le montre la figure suivante.

La fonction R (p) est représentée graphiquement. Au maximum, il y a une intersection de deux lignes pointillées et d'un texte qui se lit comme suit : « Le revenu maximum est de 50 000$ par jour lorsque le prix facturé par voiture est de 100$ par jour ». — Figure$\PageIndex{6}$ : Pour maximiser ses revenus, une société de location de voitures doit équilibrer le prix d'une location par rapport au nombre de voitures que les clients loueront à ce prix.

Exercice$\PageIndex{4}$

Une société de location de voitures facture à ses clients$p$ des dollars par jour, où$60≤p≤150$. Il a découvert que le nombre de voitures louées par jour peut être modélisé par la fonction linéaire.$n(p)=750−5p.$ Combien l'entreprise doit-elle facturer à chaque client pour maximiser ses revenus ?

Allusion: $R(p)=n×p,$où$n$ est le nombre de voitures louées et$p$ le prix facturé par voiture.

Réponse: L'entreprise doit facturer$$75$ par voiture et par jour.

Exemple$\PageIndex{5}$: Maximizing the Area of an Inscribed Rectangle

Un rectangle doit être inscrit dans l'ellipse

\[\dfrac{x^2}{4}+y^2=1. \nonumber \]

Quelles doivent être les dimensions du rectangle pour maximiser sa surface ? Quelle est la surface maximale ?

Solution

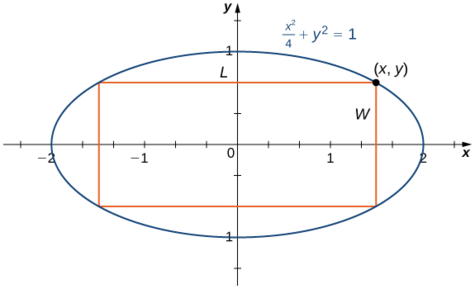
Étape 1 : Pour qu'un rectangle soit inscrit dans l'ellipse, les côtés du rectangle doivent être parallèles aux axes. $L$Soit la longueur du rectangle et$W$ sa largeur. $A$Soit l'aire du rectangle.

L'ellipse x2/4 + y2 = 1 est dessinée avec ses interceptions x étant ±2 et ses interceptions y étant ±1. Un rectangle inscrit dans l'ellipse a une longueur L (dans la direction x) et une largeur W. — Figure$\PageIndex{7}$ : Nous voulons maximiser l'aire d'un rectangle inscrit dans une ellipse.

Étape 2 : Le problème est de maximiser$A$.

Étape 3 : La surface du rectangle est$A=LW.$

Étape 4 :$(x,y)$ Soit le coin du rectangle situé dans le premier quadrant, comme indiqué sur la figure$\PageIndex{7}$. Nous pouvons écrire la longueur$L=2x$ et la largeur$W=2y$. Depuis$\dfrac{x^2}{4}+y^2=1$ et$y>0$, nous avons$y=\sqrt{1-\dfrac{x^2}{4}}$. Par conséquent, la zone est

$A=LW=(2x)(2y)=4x\sqrt{1-\dfrac{x^2}{4}}=2x\sqrt{4−x^2}$

Étape 5 : Sur la figure$\PageIndex{7}$, nous voyons que pour inscrire un rectangle dans l'ellipse, la$x$ coordonnée -du coin du premier quadrant doit satisfaire$0<x<2$. Le problème se réduit donc à la recherche de la valeur maximale de$A(x)$ sur l'intervalle ouvert$(0,2)$. Comme il y$A(x)$ aura un maximum absolu (et un minimum absolu) sur l'intervalle fermé$[0,2]$, nous considérons$A(x)=2x\sqrt{4−x^2}$ l'intervalle$[0,2]$. Si le maximum absolu se produit à un point intérieur, alors nous avons trouvé un maximum absolu dans l'intervalle ouvert.

Étape 6 : Comme mentionné précédemment,$A(x)$ est une fonction continue sur l'intervalle fermé et limité$[0,2]$. Par conséquent, il a un maximum absolu (et un minimum absolu). Aux extrémités$x=0$ et$x=2$,$A(x)=0.$ pour$0<x<2$,$A(x)>0$.

Par conséquent, le maximum doit se produire à un point critique. En prenant la dérivée de$A(x)$, on obtient

\[ \begin{align*} A'(x) &=2\sqrt{4−x^2}+2x⋅\dfrac{1}{2\sqrt{4−x^2}}(−2x) \\[4pt] &=2\sqrt{4−x^2}−\dfrac{2x^2}{\sqrt{4−x^2}} \\[4pt] &=\dfrac{8−4x^2}{\sqrt{4−x^2}} . \end{align*}\]

Pour trouver des points critiques, nous devons trouver où$A'(x)=0.$ nous pouvons voir que$x$ c'est une solution de

\[\dfrac{8−4x^2}{\sqrt{4−x^2}}=0, \label{ex5eq1} \]

alors$x$ doit satisfaire

\[8−4x^2=0. \nonumber \]

Par$x^2=2.$ conséquent,$x=±\sqrt{2}$ voici les solutions possibles de l'équation \ ref {ex5eq1}. Puisque nous examinons l'$x$intervalle$[0,2]$, il$x=\sqrt{2}$ est possible qu'un point critique soit atteint, mais ce n'$x=−\sqrt{2}$est pas le cas. Par conséquent, nous vérifions s'il s'$\sqrt{2}$agit d'une solution de l'équation \ ref {ex5eq1}. Comme$x=\sqrt{2}$ il s'agit d'une solution de l'équation \ ref {ex5eq1}, nous concluons que$\sqrt{2}$ c'est le seul point critique$A(x)$ de l'intervalle$[0,2]$.

Par conséquent,$A(x)$ doit avoir un maximum absolu au point critique$x=\sqrt{2}$. Pour déterminer les dimensions du rectangle, il faut trouver la longueur$L$ et la largeur$W$. Si$x=\sqrt{2}$ alors

\[y=\sqrt{1−\dfrac{(\sqrt{2})^2}{4}}=\sqrt{1−\dfrac{1}{2}}=\dfrac{1}{\sqrt{2}}.\nonumber \]

Les dimensions du rectangle sont donc$L=2x=2\sqrt{2}$ et$W=2y=\dfrac{2}{\sqrt{2}}=\sqrt{2}$. La surface de ce rectangle est$ A=LW=(2\sqrt{2})(\sqrt{2})=4.$

Exercice$\PageIndex{5}$

Modifiez la fonction de surface$A$ si le rectangle doit être inscrit dans le cercle unitaire$x^2+y^2=1$. Quel est le domaine à prendre en compte ?

Allusion: Si$(x,y)$ est le sommet du carré situé dans le premier quadrant, alors l'aire du carré est$A=(2x)(2y)=4xy.$

Réponse: $A(x)=4x\sqrt{1−x^2}.$Le domaine à prendre en compte est$[0,1]$.

Résolution des problèmes d'optimisation lorsque l'intervalle n'est pas fermé ou est illimité

Dans les exemples précédents, nous avons examiné les fonctions sur des domaines fermés et bornés. Par conséquent, le théorème des valeurs extrêmes nous a garanti que les fonctions avaient des extrêmes absolus. Examinons maintenant les fonctions pour lesquelles le domaine n'est ni fermé ni limité.

De nombreuses fonctions ont toujours au moins un extrême absolu, même si le domaine n'est pas fermé ou s'il est illimité. Par exemple, la fonction$f(x)=x^2+4$ over$(−∞,∞)$ a un minimum absolu de$4$ at$x=0$. Par conséquent, nous pouvons toujours considérer les fonctions sur des domaines illimités ou des intervalles ouverts et déterminer si elles présentent des extrêmes absolus. Dans l'exemple suivant, nous essayons de minimiser une fonction sur un domaine illimité. Nous verrons que, bien que le domaine à considérer soit$(0,∞),$ la fonction, elle a un minimum absolu.

Dans l'exemple suivant, nous cherchons à construire une boîte de moindre surface avec un volume prescrit. Il n'est pas difficile de montrer que pour une boîte à dessus fermé, par symétrie, parmi toutes les boîtes ayant un volume spécifié, un cube aura la plus petite surface. Par conséquent, nous examinons le problème modifié qui consiste à déterminer quelle boîte ouverte d'un volume donné possède la plus petite surface.

Exemple$\PageIndex{6}$: Minimizing Surface Area

Une boîte rectangulaire avec une base carrée, un dessus ouvert et un volume$216 \,\text{in}^3$ de doit être construite. Quelles doivent être les dimensions de la boîte pour minimiser la surface de la boîte ? Quelle est la surface minimale ?

Solution

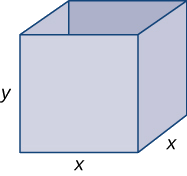
Étape 1 : Dessinez une boîte rectangulaire et introduisez la variable$x$ pour représenter la longueur de chaque côté de la base carrée ;$y$ soit la hauteur de la boîte. $S$Soit la surface de la boîte ouverte.

Une boîte à base carrée est illustrée. La base a une longueur latérale x et une hauteur y. — Figure$\PageIndex{8}$ : Nous voulons minimiser la surface d'une boîte à base carrée avec un volume donné.

Étape 2 : Nous devons minimiser la surface. Par conséquent, nous devons minimiser$S$.

Étape 3 : La partie supérieure de la boîte étant ouverte, il suffit de déterminer la surface des quatre côtés verticaux et de la base. La surface de chacun des quatre côtés verticaux est$x⋅y.$ La surface de la base est$x^2$. Par conséquent, la surface de la boîte est

$S=4xy+x^2$.

Étape 4 : Puisque le volume de cette boîte est$x^2y$ et que le volume est donné sous forme$216\,\text{in}^3$, l'équation de contrainte est

$x^2y=216$.

En résolvant l'équation de contrainte pour$y$, nous avons$y=\dfrac{216}{x^2}$. Par conséquent, nous pouvons écrire la surface en fonction$x$ uniquement de :

\[S(x)=4x\left(\dfrac{216}{x^2}\right)+x^2.\nonumber \]

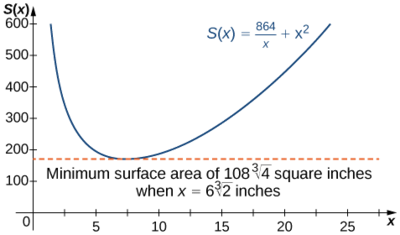
Par conséquent,$S(x)=\dfrac{864}{x}+x^2$.

Étape 5 : Puisque c'est ce que nous exigeons$x^2y=216$, nous ne pouvons pas l'avoir$x=0$. Par conséquent, nous avons besoin de$x>0$. D'autre part,$x$ est autorisé à avoir n'importe quelle valeur positive. Notez qu'au fur et à mesure que la boîte$x$ devient grande, la hauteur de la boîte$y$ devient d'autant plus petite que$x^2y=216$. De même, au fur et à$x$ mesure qu'elle devient petite, la hauteur de la boîte devient d'autant plus grande. Nous concluons que le domaine est l'intervalle ouvert et illimité$(0,∞)$. Notez que, contrairement aux exemples précédents, nous ne pouvons pas réduire notre problème à la recherche d'un maximum ou d'un minimum absolu sur un intervalle fermé et limité. Cependant, à l'étape suivante, nous découvrons pourquoi cette fonction doit avoir un minimum absolu sur l'intervalle$(0,∞).$

Étape 6 : Notez que,$x→0^+,\, S(x)→∞.$ aussi, comme$x→∞, \,S(x)→∞$. Comme$S$ il s'agit d'une fonction continue qui se rapproche de l'infini à ses extrémités, elle doit avoir un minimum absolu à certaines extrémités$x∈(0,∞)$. Ce minimum doit être atteint à un point critique de$S$. Le dérivé est

\[S′(x)=−\dfrac{864}{x^2}+2x.\nonumber \]

Par conséquent,$S′(x)=0$ quand$2x=\dfrac{864}{x^2}$. En résolvant cette équation pour$x$, nous obtenons$x^3=432$, donc$x=\sqrt[3]{432}=6\sqrt[3]{2}.$ Comme c'est le seul point critique de$S$, le minimum absolu doit se produire à$x=6\sqrt[3]{2}$ (voir Figure$\PageIndex{9}$).

Quand$x=6\sqrt[3]{2}$,$y=\dfrac{216}{(6\sqrt[3]{2})^2}=3\sqrt[3]{2}\,\text{in.}$ par conséquent, les dimensions de la boîte doivent être$x=6\sqrt[3]{2}\,\text{in.}$ et$y=3\sqrt[3]{2}\,\text{in.}$ avec ces dimensions, la surface est

\[S(6\sqrt[3]{2})=\dfrac{864}{6\sqrt[3]{2}}+(6\sqrt[3]{2})^2=108\sqrt[3]{4}\,\text{in}^2\nonumber \]

La fonction S (x) = 864/x + x2 est représentée graphiquement. Au minimum, il y a une ligne pointillée et un texte qui se lit comme suit : « La surface minimale est de 108 fois la racine cubique de 4 pouces carrés lorsque x = 6 fois la racine cubique de 2 pouces ». — Figure$\PageIndex{9}$ : Nous pouvons utiliser un graphique pour déterminer les dimensions d'une boîte en fonction du volume et de la surface minimale.

Exercice$\PageIndex{6}$

Considérez la même boîte à toit ouvert, qui doit avoir du volume$216\,\text{in}^3$. Supposons que le coût du matériau pour la base soit$20¢/\text{in}^2$ et que le coût du matériau pour les côtés l'est$30¢/\text{in}^2$ et que nous essayons de minimiser le coût de cette boîte. Écrivez le coût en fonction de la longueur des côtés de la base. ($x$Soit la longueur latérale de la base et$y$ la hauteur de la boîte.)

Allusion: Si le coût de l'un des côtés est$30¢/\text{in}^2,$ le coût de ce côté$0.30xy$ en dollars.

Réponse: $c(x)=\dfrac{259.2}{x}+0.2x^2$dollars

Concepts clés

Pour résoudre un problème d'optimisation, commencez par dessiner un tableau et introduisez des variables.
Trouvez une équation reliant les variables.
Trouvez la fonction d'une variable pour décrire la quantité qui doit être minimisée ou maximisée.
Recherchez les points critiques pour localiser les extrêmes locaux.

Lexique

problèmes d'optimisation: problèmes résolus en trouvant la valeur maximale ou minimale d'une fonction

Exemple\(\PageIndex{1}\): Maximizing the Area of a Garden

Exercice\(\PageIndex{1}\)

Stratégie de résolution de problèmes : résolution des problèmes d'optimisation

Exemple\(\PageIndex{2}\): Maximizing the Volume of a Box

Exercice\(\PageIndex{2}\)

Exemple\(\PageIndex{3}\): Minimizing Travel Time

Exercice\(\PageIndex{3}\)

Exemple\(\PageIndex{4}\): Maximizing Revenue

Exercice\(\PageIndex{4}\)

Exemple\(\PageIndex{5}\): Maximizing the Area of an Inscribed Rectangle

Exercice\(\PageIndex{5}\)

Exemple\(\PageIndex{6}\): Minimizing Surface Area

Exercice\(\PageIndex{6}\)