4.6 : Limites à l'infini et asymptotes
- Page ID
- 197698
- Calculez la limite d'une fonction sous forme d'\(x\)augmentations ou de diminutions sans limite.
- Reconnaissez une asymptote horizontale sur le graphe d'une fonction.
- Estimez le comportement final d'une fonction sous forme d'\(x\)augmentations ou de diminutions sans limite.
- Reconnaissez une asymptote oblique sur le graphe d'une fonction.
- Analysez une fonction et ses dérivées pour dessiner son graphe.
Nous avons montré comment utiliser les dérivées première et seconde d'une fonction pour décrire la forme d'un graphe. Pour représenter graphiquement une fonction\(f\) définie sur un domaine illimité, nous devons également connaître le comportement de\(f\) as\(x→±∞\). Dans cette section, nous définissons des limites à l'infini et montrons comment ces limites affectent le graphe d'une fonction. À la fin de cette section, nous décrivons une stratégie pour représenter graphiquement une fonction arbitraire\(f\).
Nous commençons par examiner ce que signifie pour une fonction le fait d'avoir une limite finie à l'infini. Ensuite, nous étudions l'idée d'une fonction avec une limite infinie à l'infini. Dans Introduction aux fonctions et aux graphes, nous avons examiné les asymptotes verticales ; dans cette section, nous traitons des asymptotes horizontales et obliques.
Limites à l'infini et asymptotes horizontales
Rappelez-vous que le\(\displaystyle \lim_{x→a}f(x)=L\) moyen\(f(x)\) devient arbitrairement proche\(L\) tant qu'\(x\)il est suffisamment proche de\(a\). Nous pouvons étendre cette idée à des limites infinies. Par exemple, considérez la fonction\(f(x)=2+\frac{1}{x}\). Comme on peut le voir graphiquement dans la figure\(\PageIndex{1}\) et numériquement dans le tableau\(\PageIndex{1}\), à mesure que les valeurs de\(x\) augmentent, les valeurs d'\(f(x)\)approche\(2\). Nous disons la limite à mesure que nous nous\(x\) rapprochons\(∞\)\(f(x)\) de nous\(2\) et écrivons\(\displaystyle \lim_{x→∞}f(x)=2\). De même\(x<0\), à mesure que les\(|x|\) valeurs augmentent, les valeurs d'\(f(x)\)approche\(2\). Nous disons la limite à mesure que nous nous\(x\) rapprochons\(−∞\)\(f(x)\) de nous\(2\) et écrivons\(\displaystyle \lim_{x→−∞}f(x)=2\).
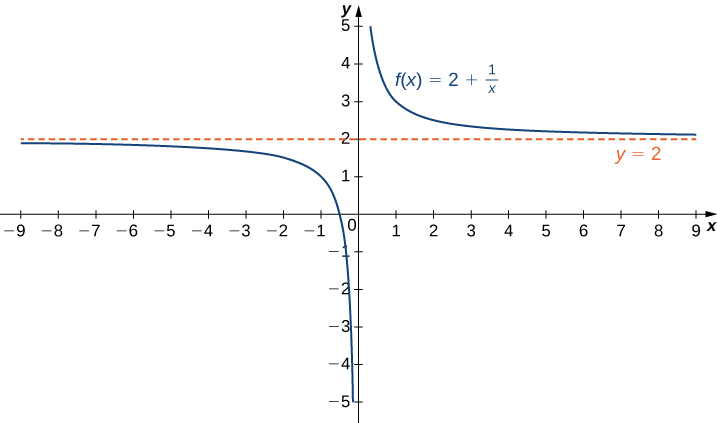
| \(x\) | 10 | 100 | 1 000 | 10 000 |
|---|---|---|---|---|
| \(2+\frac{1}{x}\) | 2.1 | 2.01 | 2,001 | 2 001 |
| \(x\) | −10 | −100 | −1000 | −10 000 |
| \(2+\frac{1}{x}\) | 1,9 | 1,99 | 1,999 | 1,999 |
Plus généralement, pour toute fonction\(f\), nous disons que\(x→∞\) la limite\(f(x)\) est\(L\) si\(f(x)\) elle devient arbitrairement proche\(L\) tant qu'elle\(x\) est suffisamment grande. Dans ce cas, nous écrivons\(\displaystyle \lim_{x→∞}f(x)=L\). De même, nous disons que\(x→−∞\) la limite\(f(x)\) est\(L\) si\(f(x)\) elle devient arbitrairement proche\(L\) tant qu'\(x<0\)elle\(|x|\) est suffisamment grande. Dans ce cas, nous écrivons\(\displaystyle \lim_{x→−∞}f(x)=L\). Nous examinons maintenant la définition d'une fonction ayant une limite à l'infini.
Si les valeurs de\(f(x)\) deviennent arbitrairement proches de z\(L\)\(x\) deviennent suffisamment grandes, nous disons que la fonction\(f\) a une limite à l'infini et écrivons
\[\lim_{x→∞}f(x)=L. \nonumber \]
Si les valeurs de\(f(x)\) deviennent arbitrairement proches de\(L\) for\(x<0\) as\(|x|\) deviennent suffisamment grandes, nous disons que la fonction\(f\) a une limite à l'infini négatif et écrivons
\[\lim_{x→−∞}f(x)=L. \nonumber \]
Si les valeurs se\(f(x)\) rapprochent arbitrairement d'une valeur finie au\(L\) fur et à mesure que\(x→∞\) ou\(x→−∞\), le graphe de\(f\) s'approche de la droite\(y=L\). Dans ce cas, la droite\(y=L\) est une asymptote horizontale de\(f\) (Figure\(\PageIndex{2}\)). Par exemple, pour la fonction\(f(x)=\dfrac{1}{x}\), puisque\(\displaystyle \lim_{x→∞}f(x)=0\), la ligne\(y=0\) est une asymptote horizontale de\(f(x)=\dfrac{1}{x}\).

Si\(\displaystyle \lim_{x→∞}f(x)=L\) ou\(\displaystyle \lim_{x→−∞}f(x)=L\), nous disons que la ligne\(y=L\) est une asymptote horizontale de\(f\).
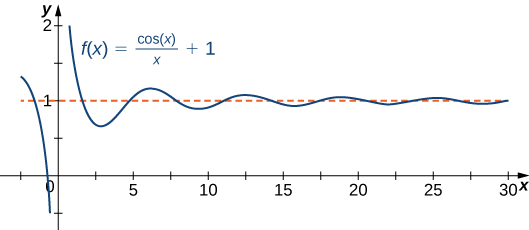
Une fonction ne peut pas traverser une asymptote verticale car le graphe doit s'approcher de l'infini (ou\( −∞\)) dans au moins une direction lorsqu'il\(x\) s'approche de l'asymptote verticale. Cependant, une fonction peut traverser une asymptote horizontale. En fait, une fonction peut traverser une asymptote horizontale un nombre illimité de fois. Par exemple, la fonction\(f(x)=\dfrac{\cos x}{x}+1\) illustrée dans la figure\(\PageIndex{3}\) croise l'asymptote horizontale\(y=1\) un nombre infini de fois alors qu'elle oscille autour de l'asymptote avec une amplitude toujours décroissante.
Les lois algébriques des limites et le théorème de compression que nous avons introduits dans Introduction aux limites s'appliquent également aux limites à l'infini. Nous illustrons comment utiliser ces lois pour calculer plusieurs limites à l'infini.
Pour chacune des fonctions suivantes\(f\), évaluez\(\displaystyle \lim_{x→∞}f(x)\) et\(\displaystyle \lim_{x→−∞}f(x)\). Déterminez la ou les asymptotes horizontales pour\(f\).
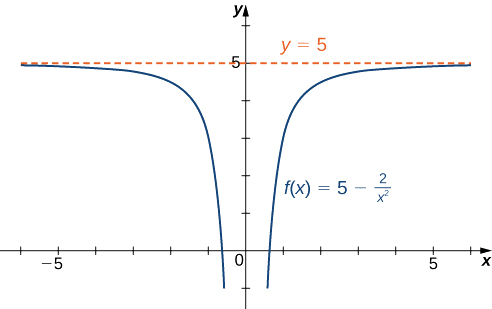
- \(f(x)=5−\dfrac{2}{x^2}\)
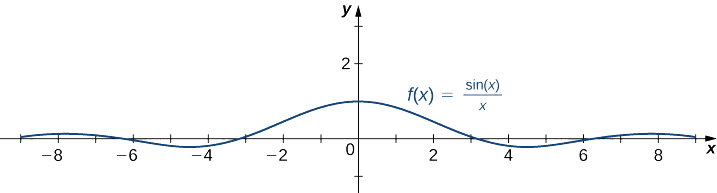
- \(f(x)=\dfrac{\sin x}{x}\)
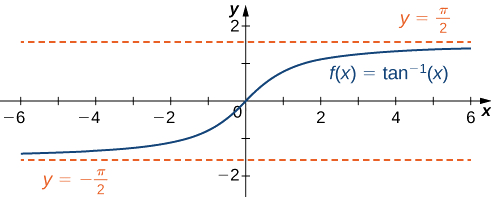
- \(f(x)=\tan^{−1}(x)\)
Solution
a. En utilisant les lois des limites algébriques, nous avons
\[\lim_{x→∞}\left(5−\frac{2}{x^2}\right)=\lim_{x→∞}5−2\left(\lim_{x→∞}\frac{1}{x}\right)\cdot\left(\lim_{x→∞}\frac{1}{x}\right)=5−2⋅0=5.\nonumber \]
De même,\(\displaystyle \lim_{x→−∞}f(x)=5\). Par conséquent,\(f(x)=5-\dfrac{2}{x^2}\) possède une asymptote horizontale\(y=5\) et s'\(f\)approche de cette asymptote horizontale\(x→±∞\) comme indiqué dans le graphique suivant.
b. Puisque\(-1≤\sin x≤1\) pour tous\(x\), nous avons
\[\frac{−1}{x}≤\frac{\sin x}{x}≤\frac{1}{x}\nonumber \]
pour tous\(x≠0\). En outre, puisque
\(\displaystyle \lim_{x→∞}\frac{−1}{x}=0=\lim_{x→∞}\frac{1}{x}\),
nous pouvons appliquer le théorème de compression pour conclure que
\(\displaystyle \lim_{x→∞}\frac{\sin x}{x}=0.\)
De même,
\(\displaystyle \lim_{x→−∞}\frac{\sin x}{x}=0.\)
Ainsi,\(f(x)=\dfrac{\sin x}{x}\) possède une asymptote horizontale\(y=0\) et s'\(f(x)\)approche de cette asymptote horizontale\(x→±∞\) comme indiqué dans le graphique suivant.
c. Pour évaluer\(\displaystyle \lim_{x→∞}\tan^{−1}(x)\) et\(\displaystyle \lim_{x→−∞}\tan^{−1}(x)\), nous considérons d'abord le graphique de l'\(y=\tan(x)\)intervalle,\(\left(−\frac{π}{2},\frac{π}{2}\right)\) comme indiqué dans le graphique suivant.
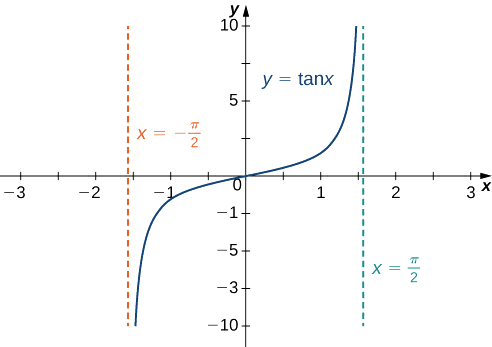
Depuis
\(\displaystyle \lim_{x→\tfrac{π}{2}^−}\tan x=∞,\)
il s'ensuit que
\(\displaystyle \lim_{x→∞}\tan^{−1}(x)=\frac{π}{2}.\)
De même, puisque
\(\displaystyle \lim_{x→-\tfrac{π}{2}^+}\tan x=−∞,\)
il s'ensuit que
\(\displaystyle \lim_{x→−∞}\tan^{−1}(x)=−\frac{π}{2}.\)
Par conséquent,\(y=\frac{π}{2}\) et\(y=−\frac{π}{2}\) sont des asymptotes horizontales de,\(f(x)=\tan^{−1}(x)\) comme indiqué dans le graphique suivant.
Évaluez\(\displaystyle \lim_{x→−∞}\left(3+\frac{4}{x}\right)\) et\(\displaystyle \lim_{x→∞}\left(3+\dfrac{4}{x}\right)\). Déterminez les asymptotes horizontales,\(f(x)=3+\frac{4}{x},\) le cas échéant.
- Allusion
-
\(\displaystyle \lim_{x→±∞}\frac{1}{x}=0\)
- Réponse
-
Les deux limites sont\(3.\) La ligne\(y=3\) est une asymptote horizontale.
Des limites infinies à l'infini
Parfois, les valeurs d'une fonction\(f\) deviennent arbitrairement grandes en tant que\(x→∞ \) (ou as\(x→−∞\)). Dans ce cas, nous écrivons\(\displaystyle \lim_{x→∞}f(x)=∞\) (ou\(\displaystyle \lim_{x→−∞}f(x)=∞\)). En revanche, si les valeurs de\(f\) sont négatives mais deviennent arbitrairement importantes au fur et à mesure que\(x→∞\) (ou as\(x→−∞\)), on écrit\(\displaystyle \lim_{x→∞}f(x)=−∞\) (ou\(\displaystyle \lim_{x→−∞}f(x)=−∞\)).
Par exemple, considérez la fonction\(f(x)=x^3\). Comme le montrent le tableau\(\PageIndex{2}\) et la figure\(\PageIndex{8}\),\(x→∞\) lorsque les valeurs\(f(x)\) deviennent arbitrairement grandes. Par conséquent,\(\displaystyle \lim_{x→∞}x^3=∞\). D'autre part\(x→−∞\), les valeurs de\(f(x)=x^3\) sont négatives mais deviennent arbitrairement importantes. Par conséquent,\(\displaystyle \lim_{x→−∞}x^3=−∞.\)
| \(x\) | 10 | 20 | 50 | 100 | 1000 |
|---|---|---|---|---|---|
| \(x^3\) | 1000 | 8000 | 125 000 | 1 000 000 | 1 000 000 000 |
| \(x\) | −10 | −20 | −50 | −100 | −1000 |
| \(x^3\) | −1000 | −8 000 | −125 000 | −1 000 000 | −1 000 000 000 |
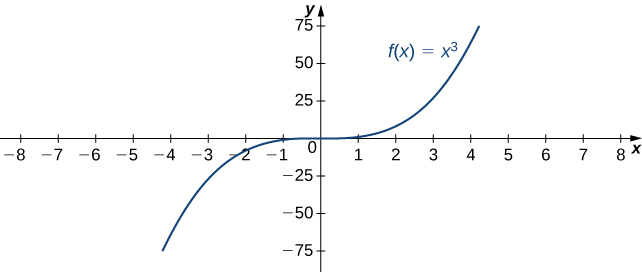
Nous disons qu'une fonction\(f\) a une limite infinie à l'infini et écrivons
\[\lim_{x→∞}f(x)=∞. \nonumber \]
elle\(f(x)\) devient arbitrairement grande pour\(x\) être suffisamment grande. Nous disons qu'une fonction a une limite infinie négative à l'infini et écrivons
\[\lim_{x→∞}f(x)=−∞. \nonumber \]
si\(f(x)<0\) et\(|f(x)|\) devient arbitrairement grand pour\(x\) suffisamment grand. De même, nous pouvons définir des limites infinies comme\(x→−∞.\)
Définitions formelles
Auparavant, nous avons utilisé les termes « arbitrairement proche », « arbitrairement large » et « suffisamment grand » pour définir des limites à l'infini de manière informelle. Bien que ces termes fournissent des descriptions précises des limites à l'infini, ils ne sont pas précis mathématiquement. Voici des définitions plus formelles des limites à l'infini. Nous verrons ensuite comment utiliser ces définitions pour prouver des résultats impliquant des limites infinies.
Nous disons qu'une fonction\(f\) a une limite à l'infini, s'il existe un nombre réel\(L\) tel que pour tous\(ε>0\), il existe\(N>0\) tel que
\[|f(x)−L|<ε \nonumber \]
pour tous,\(x>N.\) dans ce cas, nous écrivons
\[\lim_{x→∞}f(x)=L \nonumber \]
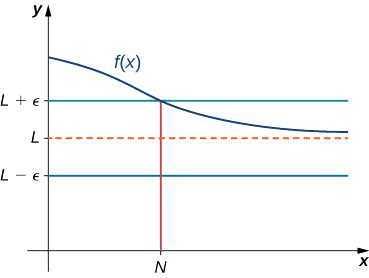
Plus tôt dans cette section, nous avons utilisé des preuves graphiques dans la figure\(\PageIndex{1}\) et des preuves numériques dans le tableau\(\PageIndex{1}\) pour conclure que\(\displaystyle \lim_{x→∞}\left(2+\frac{1}{x}\right)=2\). Nous utilisons ici la définition formelle de la limite à l'infini pour prouver rigoureusement ce résultat.
Utilisez la définition formelle de la limite à l'infini pour le prouver\(\displaystyle \lim_{x→∞}\left(2+\frac{1}{x}\right)=2\).
Solution
Laisse\(ε>0.\) laisser\(N=\frac{1}{ε}\). Par conséquent, pour tous\(x>N\), nous avons
\[\left|2+\frac{1}{x}−2\right|=\left|\frac{1}{x}\right|=\frac{1}{x}<\frac{1}{N}=ε \nonumber \]
Utilisez la définition formelle de la limite à l'infini pour le prouver\(\displaystyle \lim_{x→∞}\left(3-\frac{1}{x^2}\right)=3\).
- Allusion
-
Laissez\(N=\frac{1}{\sqrt{ε}}\).
- Réponse
-
Laisse\(ε>0.\) laisser\(N=\frac{1}{\sqrt{ε}}\). Par conséquent, pour tout ce\(x>N,\) que nous avons
\[\Big|3−\frac{1}{x^2}−3\Big|=\frac{1}{x^2}<\frac{1}{N^2}=ε \nonumber \]
Par conséquent,\(\displaystyle \lim_{x→∞}(3−1/x^2)=3.\)
Nous allons maintenant porter notre attention sur une définition plus précise d'une limite infinie à l'infini.
Nous disons qu'une fonction\(f\) a une limite infinie à l'infini et écrivons
\(\displaystyle \lim_{x→∞}f(x)=∞\)
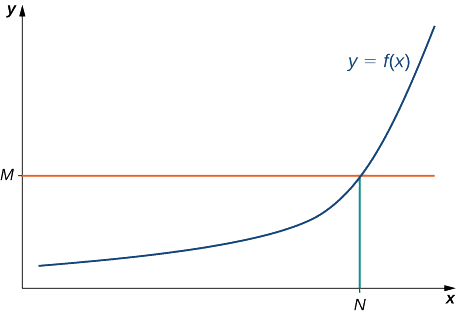
si pour tous\(M>0,\) il existe un\(N>0\) tel que
\(f(x)>M\)
pour tous\(x>N\) (voir Figure\(\PageIndex{10}\)).
Nous disons qu'une fonction a une limite infinie négative à l'infini et écrivons
\(\displaystyle \lim_{x→∞}f(x)=−∞\)
si pour tous\(M<0\), il existe un\(N>0\) tel que
\(f(x)<M\)
pour tous\(x>N\).
De même, nous pouvons définir des limites comme\(x→−∞.\)
Plus tôt, nous avons utilisé des preuves graphiques (Figure\(\PageIndex{8}\)) et des preuves numériques (Tableau\(\PageIndex{2}\)) pour en arriver à cette conclusion\(\displaystyle \lim_{x→∞}x^3=∞\). Nous utilisons ici la définition formelle de la limite infinie à l'infini pour prouver ce résultat.
Utilisez la définition formelle de la limite infinie à l'infini pour prouver que\(\displaystyle \lim_{x→∞}x^3=∞.\)
Solution
Laisse\(M>0.\) laisser\(N=\sqrt[3]{M}\). Alors, pour tous\(x>N\), nous avons
\(x^3>N^3=(\sqrt[3]{M})^3=M.\)
Par conséquent,\(\displaystyle \lim_{x→∞}x^3=∞\).
Utilisez la définition formelle de la limite infinie à l'infini pour prouver que\(\displaystyle \lim_{x→∞}3x^2=∞.\)
- Allusion
-
Laissez\(N=\sqrt{\frac{M}{3}}\).
- Réponse
-
Laisse\(M>0.\) laisser\(N=\sqrt{\frac{M}{3}}\). Alors, pour tout ce\(x>N,\) que nous avons
\(3x^2>3N^2=3\left(\sqrt{\frac{M}{3}}\right)^2=\frac{3M}{3}=M\)
Comportement final
Le comportement d'une fonction\(x→±∞\) est appelé comportement final de la fonction. À chacune des extrémités de la fonction, celle-ci peut présenter l'un des types de comportement suivants :
- La fonction se\(f(x)\) rapproche d'une asymptote horizontale\(y=L\).
- La fonction\(f(x)→∞\) ou\(f(x)→−∞.\)
- La fonction ne s'approche pas d'une limite finie, pas plus qu'elle ne s'approche de\(∞\) ou\(−∞\). Dans ce cas, la fonction peut avoir un certain comportement oscillatoire.
Examinons ici plusieurs classes de fonctions et examinons les différents types de comportements finaux pour ces fonctions.
Comportement final pour les fonctions polynomiales
Considérez la fonction de puissance\(f(x)=x^n\) où\(n\) est un entier positif. D'après Figure\(\PageIndex{11}\) and Figure\(\PageIndex{12}\), nous voyons que
\[\lim_{x→∞}x^n=∞;\;n=1,2,3,… \nonumber \]
et
\[\lim_{x→−∞}x^n=\begin{cases}∞, & n=2,4,6,…\\−∞, & n=1,3,5,….\end{cases} \nonumber \]
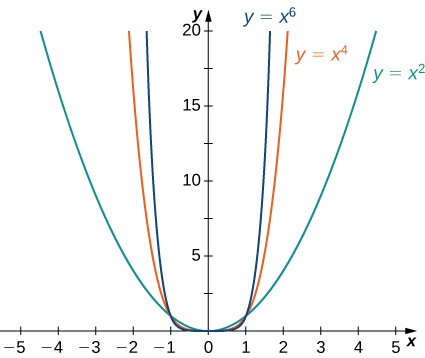
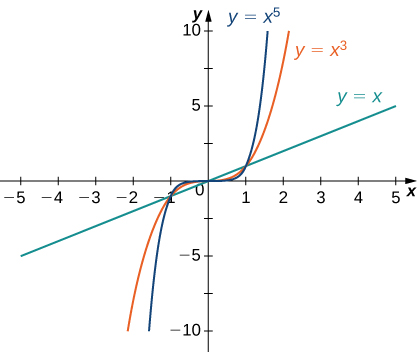
En utilisant ces faits, il n'est pas difficile d'évaluer\(\displaystyle \lim_{x→∞}cx^n\) et\(\displaystyle \lim_{x→−∞}cx^n\), où\(c\) est une constante et\(n\) un entier positif. Si\(c>0\), le graphique de\(y=cx^n\) est un étirement vertical ou une compression de\(y=x^n,\) et donc
\(\displaystyle \lim_{x→∞}cx^n=\lim_{x→∞}x^n\)et\(\displaystyle \lim_{x→−∞}cx^n=\lim_{x→−∞}x^n\) si\(c>0\).
Si\(c<0,\) le graphique de\(y=cx^n\) est un étirement vertical ou une compression combiné à une réflexion autour de l'\(x\)axe des Y, et donc
\(\displaystyle \lim_{x→∞}cx^n=−\lim_{x→∞}x^n\)et\(\displaystyle \lim_{x→−∞}cx^n=−\lim_{x→−∞}x^n\) si\(c<0.\)
Si\(c=0,y=cx^n=0,\) dans quel cas\(\displaystyle \lim_{x→∞}cx^n=0=\lim_{x→−∞}cx^n.\)
Pour chaque fonction\(f\), évaluez\(\displaystyle \lim_{x→∞}f(x)\) et\(\displaystyle \lim_{x→−∞}f(x)\).
- \(f(x)=−5x^3\)
- \(f(x)=2x^4\)
Solution
- Puisque le coefficient de\(x^3\) est\(−5\), le graphe de\(f(x)=−5x^3\) implique un étirement vertical et une réflexion du graphe\(y=x^3\) autour de l'\(x\)axe. Par conséquent,\(\displaystyle \lim_{x→∞}(−5x^3)=−∞\) et\(\displaystyle \lim_{x→−∞}(−5x^3)=∞\).
- Puisque le coefficient de\(x^4\) est\(2\), le graphe de\(f(x)=2x^4\) est un étirement vertical du graphe de\(y=x^4\). Par conséquent,\(\displaystyle \lim_{x→∞}2x^4=∞\) et\(\displaystyle \lim_{x→−∞}2x^4=∞\).
Laissez\(f(x)=−3x^4\). Trouvez\(\displaystyle \lim_{x→∞}f(x)\).
- Allusion
-
Le coefficient\(−3\) est négatif.
- Réponse
-
\(−∞\)
Nous examinons maintenant comment les limites infinies des fonctions de puissance peuvent être utilisées\(\displaystyle \lim_{x→±∞}f(x)\) pour déterminer n'importe quelle fonction polynomiale\(f\). Considérons une fonction polynomiale
\[f(x)=a_nx^n+a_{n−1}x^{n−1}+…+a^1x+a^0 \nonumber \]
de diplôme, de\(n≥1\) sorte que\(a_n≠0.\)
L'affacturage, nous voyons que
\[f(x)=a_nx^n\left(1+\frac{a_{n−1}}{a_n}\frac{1}{x}+…+\frac{a_1}{a_n}\frac{1}{x^{n−1}}+\frac{a_0}{a_n}\frac{1}{x^n}\right). \nonumber \]
Comme\(x→±∞,\) tous les termes entre parenthèses approchent de zéro, sauf le premier terme. Nous concluons que
\[\lim_{x→±∞}f(x)=\lim_{x→±∞}a_nx^n. \nonumber \]
Par exemple, la fonction\(f(x)=5x^3−3x^2+4\) se comporte\(g(x)=5x^3\)\(x→±∞\) comme indiqué dans Figure\(\PageIndex{13}\) et Tableau\(\PageIndex{3}\).
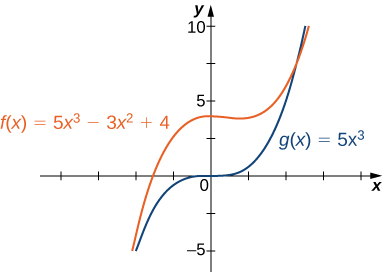
| \(x\) | 10 | 100 | 1000 |
|---|---|---|---|
| \(f(x)=5x^3−3x^2+4\) | 4704 | 4 970 004 | 4 997 000 004 |
| \(g(x)=5x^3\) | 5000 | 5 000 000 | 5 000 000 000 |
| \(x\) | −10 | −100 | −000 |
| \(f(x)=5x^3−3x^2+4\) | −5296 | −5 029 996 | −5 002 999 996 |
| \(g(x)=5x^3\) | −5 000 | −5 000 000 | −5 000 000 000 |
Comportement final pour les fonctions algébriques
Le comportement final des fonctions rationnelles et des fonctions impliquant des radicaux est un peu plus compliqué que pour les polynômes. Dans l'exemple\(\PageIndex{5}\), nous montrons que les limites à l'infini d'une fonction rationnelle\(f(x)=\dfrac{p(x)}{q(x)}\) dépendent de la relation entre le degré du numérateur et le degré du dénominateur. Pour évaluer les limites à l'infini d'une fonction rationnelle, nous divisons le numérateur et le dénominateur par la puissance la plus élevée\(x\) apparaissant dans le dénominateur. Cela détermine quel terme de l'expression globale domine le comportement de la fonction à des valeurs élevées de\(x\).
Pour chacune des fonctions suivantes, déterminez les limites au fur\(x→∞\) et à mesure,\(x→−∞.\) puis utilisez ces informations pour décrire le comportement final de la fonction.
- \(f(x)=\dfrac{3x−1}{2x+5}\)(Remarque : Le degré du numérateur et le dénominateur sont identiques.)
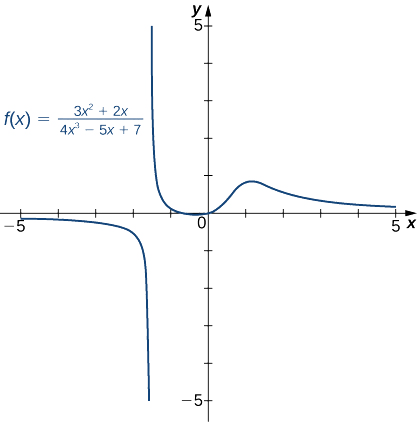
- \(f(x)=\dfrac{3x^2+2x}{4x^3−5x+7}\)(Remarque : Le degré du numérateur est inférieur au degré du dénominateur.)
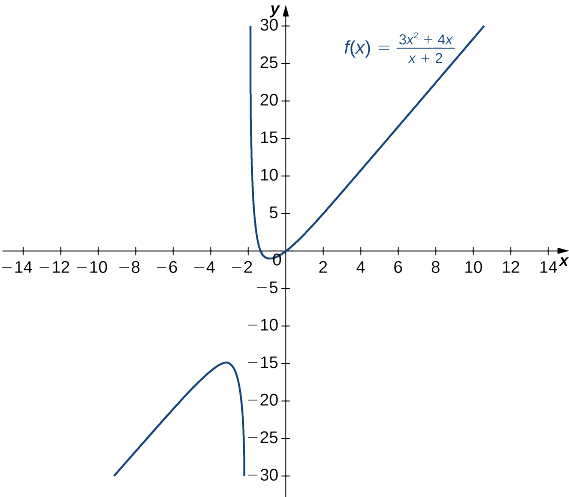
- \(f(x)=\dfrac{3x^2+4x}{x+2}\)(Remarque : Le degré du numérateur est supérieur au degré du dénominateur.)
Solution
a. La puissance la plus élevée\(x\) du dénominateur est\(x\). Par conséquent, en divisant le numérateur et le dénominateur par\(x\) et en appliquant les lois des limites algébriques, nous voyons que
\[ \begin{align*} \lim_{x→±∞}\frac{3x−1}{2x+5} &=\lim_{x→±∞}\frac{3−1/x}{2+5/x} \\[4pt] &=\frac{\lim_{x→±∞}(3−1/x)}{\lim_{x→±∞}(2+5/x)} \\[4pt] &=\frac{\lim_{x→±∞}3−\lim_{x→±∞}1/x}{\lim_{x→±∞}2+\lim_{x→±∞}5/x} \\[4pt] &=\frac{3−0}{2+0}=\frac{3}{2}. \end{align*}\]
Puisque\(\displaystyle \lim_{x→±∞}f(x)=\frac{3}{2}\), nous savons qu'il\(y=\frac{3}{2}\) s'agit d'une asymptote horizontale pour cette fonction, comme le montre le graphique suivant.
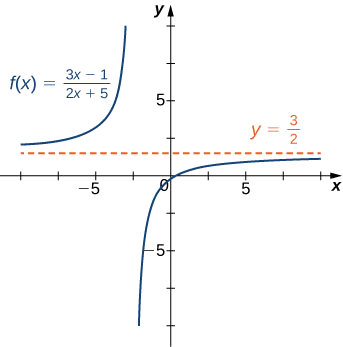
b. Puisque la plus grande puissance\(x\) apparaissant dans le dénominateur est\(x^3\) de diviser le numérateur et le dénominateur par\(x^3\). Après avoir fait cela et appliqué des lois limites algébriques, nous obtenons
\[\lim_{x→±∞}\frac{3x^2+2x}{4x^3−5x+7}=\lim_{x→±∞}\frac{3/x+2/x^2}{4−5/x^2+7/x^3}=\frac{3\cdot 0+2\cdot 0}{4−5\cdot 0+7\cdot 0}=\frac{0}{4}=0. \nonumber \]
Il\(f\) a donc une asymptote horizontale\(y=0\) comme indiqué dans le graphique suivant.
c. En divisant le numérateur et le dénominateur par\(x\), nous avons
\[\displaystyle \lim_{x→±∞}\frac{3x^2+4x}{x+2}=\lim_{x→±∞}\frac{3x+4}{1+2/x}. \nonumber \]
Au fur\(x→±∞\) et à mesure que le dénominateur approche\(1\). À mesure que\(x→∞\) le numérateur approche\(+∞\). À mesure que\(x→−∞\) le numérateur approche\(−∞\). Par conséquent\(\displaystyle \lim_{x→∞}f(x)=∞\), alors\(\displaystyle \lim_{x→−∞}f(x)=−∞\) que comme le montre la figure suivante.
Évaluez\(\displaystyle \lim_{x→±∞}\frac{3x^2+2x−1}{5x^2−4x+7}\) et utilisez ces limites pour déterminer le comportement final de\(f(x)=\dfrac{3x^2+2x−1}{5x^2−4x+7}\).
- Allusion
-
Divisez le numérateur et le dénominateur par\(x^2\).
- Réponse
-
\(\frac{3}{5}\)
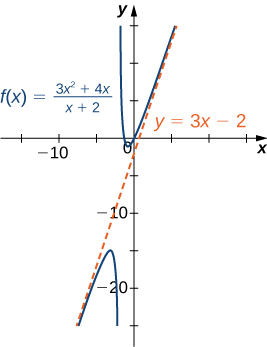
Avant de continuer, considérez le graphique de la\(f(x)=\dfrac{3x^2+4x}{x+2}\) figure\(\PageIndex{16}\). Au fur\(x→∞\) et à mesure\(x→−∞\), le graphe de\(f\) apparaît presque linéaire. Bien qu'\(f\)il ne s'agisse certainement pas d'une fonction linéaire, nous étudions maintenant pourquoi le graphe de\(f\) semble s'approcher d'une fonction linéaire. Tout d'abord, en utilisant la division longue des polynômes, nous pouvons écrire
\[f(x)=\frac{3x^2+4x}{x+2}=3x−2+\frac{4}{x+2}. \nonumber \]
Étant donné\(\dfrac{4}{x+2}→0\) que\(x→±∞,\) nous concluons que
\[ \lim_{x→±∞}(f(x)−(3x−2))=\lim_{x→±∞}\frac{4}{x+2}=0. \nonumber \]
Par conséquent, le graphique de\(f\) s'approche de la droite\(y=3x−2\) comme\(x→±∞\). Cette ligne est connue sous le nom d'asymptote oblique pour\(f\) (Figure\(\PageIndex{17}\)).
Nous pouvons résumer les résultats de l'exemple\(\PageIndex{5}\) pour tirer la conclusion suivante concernant le comportement final des fonctions rationnelles. Considérez une fonction rationnelle
\[f(x)=\frac{p(x)}{q(x)}=\frac{a_nx^n+a_{n−1}x^{n−1}+…+a_1x+a_0}{b_mx^m+b_{m−1}x^{m−1}+…+b_1x+b_0},\nonumber \]
où\(a_n≠0\) et\(b_m≠0.\)
- Si le degré du numérateur est identique au degré du dénominateur\((n=m),\), alors\(f\) a une asymptote horizontale de\(y=a_n/b_m\)\(x→±∞.\)
- Si le degré du numérateur est inférieur au degré du dénominateur\((n<m),\), il\(f\) a une asymptote horizontale\(y=0\) de\(x→±∞.\)
- Si le degré du numérateur est supérieur au degré du dénominateur\((n>m),\), il\(f\) n'a pas d'asymptote horizontale. Les limites à l'infini sont infinies positives ou négatives, selon les signes des termes principaux. De plus, en utilisant une division longue, la fonction peut être réécrite comme\[f(x)=\frac{p(x)}{q(x)}=g(x)+\frac{r(x)}{q(x)}, \nonumber \] si le degré de\(r(x)\) est inférieur au degré de\(q(x)\). Par conséquent,\(\displaystyle \lim_{x→±∞}r(x)/q(x)=0\). Par conséquent, les valeurs de zéro\([f(x)−g(x)]\) s'approchent de zéro comme\(x→±∞\). Si le degré de\(p(x)\) est exactement supérieur d'un au degré de\(q(x)\) (c'est-à-dire\(n=m+1\)), la fonction\(g(x)\) est une fonction linéaire. Dans ce cas, nous appelons\(g(x)\) asymptote oblique.
Examinons maintenant le comportement final des fonctions impliquant un radical.
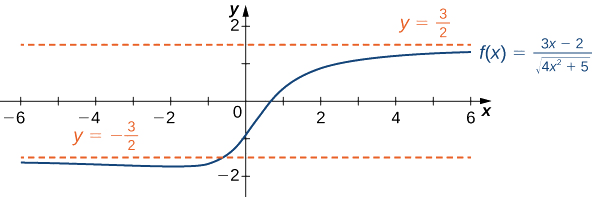
Trouvez les limites au fur\(x→∞\) et\(x→−∞\) à mesure\(f(x)=\dfrac{3x−2}{\sqrt{4x^2+5}}\) et décrivez le comportement final de\(f\).
Solution
Utilisons la même stratégie que pour les fonctions rationnelles : divisez le numérateur et le dénominateur par une puissance de\(x\). Pour déterminer la puissance appropriée de\(x\), considérez\(\sqrt{4x^2+5}\) l'expression du dénominateur. Depuis
\[\sqrt{4x^2+5}≈\sqrt{4x^2}=2|x| \nonumber \]
pour de grandes valeurs,\(x\) en fait,\(x\) apparaît juste à la première puissance du dénominateur. Par conséquent, nous divisons le numérateur et le dénominateur par\(|x|\). Ensuite, en utilisant le fait que\(|x|=x\)\(x>0, |x|=−x\) pour\(x<0\) et\(|x|=\sqrt{x^2}\) pour tous\(x\), nous calculons les limites comme suit :
\ [\ begin {align*} \ lim_ {x→∞} \ frac {3x−2} {\ sqrt {4x^2+5}} &= \ lim_ {x→∞} \ frac {(1/|x|) (3x−2)} {(1/|x|) \ sqrt {4x^2+5}} \ \ [4 points]
&= \ lim_ {→∞} \ frac {(1/x) (3x−2)} {\ sqrt {(1/x^2) (4x^2+5)}} \ \ [4 points]
&= \ lim_ {x→∞} \ frac {3−2/x} {\ sqrt {4+5/x^2}} = \ frac {3} {\ sqrt {4}} = \ frac {3} {2} \ end {align*} \]
\ [\ begin {align*} \ lim_ {x→−∞} \ frac {3x−2} {\ sqrt {4x^2+5}} &= \ lim_ {x→−∞} \ frac {(1/|x|) (3x−2)} {(1/|x|) \ sqrt {4x^2+5}} \ \ [4 points]
&= \ lim_ {x| →−∞} \ frac {(−1/x) (3x−2)} {\ sqrt {(1/x^2) (4x^2+5)}} \ \ [4 points]
&= \ lim_ {x→−∞} \ frac {−3+2/x} {\ sqrt {4+5/x^2}} = \ frac {−3} {\ sqrt {4}} = \ frac {−3} {2}. \ end {align*} \]
Par conséquent,\(f(x)\) s'approche de l'asymptote horizontale\(y=\frac{3}{2}\) en tant que\(x→∞\) et de l'asymptote horizontale\(y=−\frac{3}{2}\)\(x→−∞\) comme indiqué dans le graphique suivant.
Évaluer\(\displaystyle \lim_{x→∞}\frac{\sqrt{3x^2+4}}{x+6}\).
- Allusion
-
Divisez le numérateur et le dénominateur par\(x\).
- Réponse
-
\(\sqrt{3}\)
Déterminer le comportement final pour les fonctions transcendantales
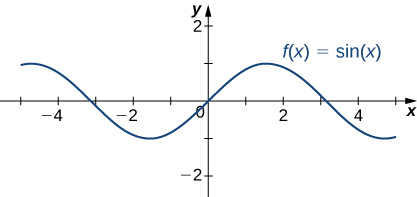
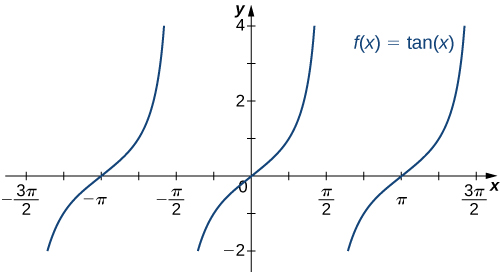
Les six fonctions trigonométriques de base sont périodiques et ne s'approchent pas d'une limite finie car, par\(x→±∞.\) exemple,\(\sin x\) oscillent entre 1 et -1 (Figure\(\PageIndex{19}\)). La fonction tangente\(x\) possède un nombre infini d'asymptotes verticales\(x→±∞\) ; par conséquent, elle ne s'approche pas d'une limite finie et ne s'approche pas\(±∞\)\(x→±∞\) comme indiqué sur la figure\(\PageIndex{20}\).
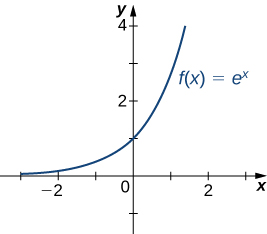
Rappelez-vous que pour n'importe quelle base,\(b>0,\; b≠1,\) la fonction\(y=b^x\) est une fonction exponentielle avec domaine\((−∞,∞)\) et plage\((0,∞)\). \(b>1,\;y=b^x\)Il augmente de plus en plus\((−∞,∞)\). \(0<b<1, \; y=b^x\)Il est décroissant par rapport\((−∞,∞).\) à Pour la fonction exponentielle naturelle\(f(x)=e^x, \; e≈2.718>1\). Par conséquent,\(f(x)=e^x\) augmente\((−∞,∞)\) et la portée est\((0,∞)\). La fonction exponentielle\(f(x)=e^x\) s'approche\(∞\)\(x→∞\) et s'approche\(0\)\(x→−∞\) comme indiqué dans le tableau\(\PageIndex{4}\) et la figure\(\PageIndex{21}\).
| \(x\) | −5 | −2 | 0 | 2 | 5 |
|---|---|---|---|---|---|
| \(e^x\) | 0,00674 | 0,135 | 1 | 7 389 | 148.413 |
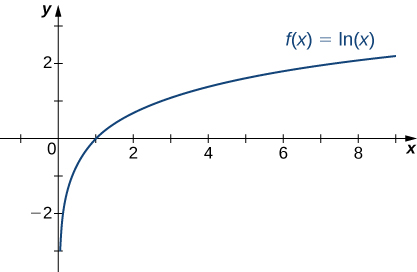
Rappelons que la fonction logarithmique naturelle\(f(x)=\ln(x)\) est l'inverse de la fonction exponentielle naturelle\(y=e^x\). Par conséquent, le domaine de\(f(x)=\ln(x)\) est\((0,∞)\) et la gamme est\((−∞,∞)\). Le graphe de\(f(x)=\ln(x)\) est le reflet du graphe d'\(y=e^x\)environ la ligne\(y=x\). Par conséquent,\(\ln(x)→−∞\)\(\ln(x)→∞\)\(x→∞\) comme\(x→0^+\) indiqué dans la figure\(\PageIndex{22}\) et le tableau\(\PageIndex{5}\).
| \(x\) | 0,01 | 0,1 | 1 | 10 | 100 |
|---|---|---|---|---|---|
| \(\ln(x)\) | −4 605 | −2,303 | 0 | 2.303 | 4.605 |
Trouvez les limites au fur\(x→∞\) et\(x→−∞\) à mesure\(f(x)=\dfrac{2+3e^x}{7−5e^x}\) et décrivez le comportement final de\(f.\)
Solution
Pour trouver la limite,\(x→∞,\) divisez le numérateur et le dénominateur par\(e^x\) :
\[ \begin{align*} \lim_{x→∞}f(x) &= \lim_{x→∞}\frac{2+3e^x}{7−5e^x} \\[4pt] &=\lim_{x→∞}\frac{(2/e^x)+3}{(7/e^x)−5.} \end{align*}\]
Comme le montre la figure\(\PageIndex{21}\),\(e^x→∞\) comme\(x→∞\). Par conséquent,
\(\displaystyle \lim_{x→∞}\frac{2}{e^x}=0=\lim_{x→∞}\frac{7}{e^x}\).
Nous concluons que\(\displaystyle \lim_{x→∞}f(x)=−\frac{3}{5}\), et le graphe des\(f\) approches de l'asymptote horizontale\(y=−\frac{3}{5}\) comme\(x→∞.\) Pour trouver la limite comme\(x→−∞\), utilisez le fait que\(e^x→0\)\(x→−∞\) pour conclure que\(\displaystyle \lim_{x→-∞}f(x)=\frac{2}{7}\), et donc le graphe des\(f(x)\) approches de l'asymptote horizontale \(y=\frac{2}{7}\)comme\(x→−∞\).
Trouvez les limites au fur\(x→∞\) et\(x→−∞\) à mesure\(f(x)=\dfrac{3e^x−4}{5e^x+2}\).
- Allusion
-
\(\displaystyle \lim_{x→∞}e^x=∞\)et\(\displaystyle \lim_{x→-∞}e^x=0.\)
- Réponse
-
\(\displaystyle \lim_{x→∞}f(x)=\frac{3}{5}, \quad\lim_{x→−∞}f(x)=−2\)
Instructions pour dessiner le graphe d'une fonction
Nous disposons désormais de suffisamment d'outils analytiques pour tracer des graphes d'une grande variété de fonctions algébriques et transcendantales. Avant de montrer comment représenter graphiquement des fonctions spécifiques, examinons une stratégie générale à utiliser pour représenter graphiquement n'importe quelle fonction.
Pour une fonction donnée\(f\), procédez comme suit pour esquisser un graphe de\(f\) :
- Déterminez le domaine de la fonction.
- Localisez les\(y\) interceptions\(x\) - et -.
- Évaluez\(\displaystyle \lim_{x→∞}f(x)\) et\(\displaystyle \lim_{x→−∞}f(x)\) déterminez le comportement final. Si l'une de ces limites est un nombre fini\(L\), il\(y=L\) s'agit d'une asymptote horizontale. Si l'une de ces limites est\(∞\) ou\(−∞\), déterminez si\(f\) elle présente une asymptote oblique. \(f\)C'est une fonction rationnelle telle que\(f(x)=\dfrac{p(x)}{q(x)}\), lorsque le degré du numérateur est supérieur au degré du dénominateur, elle\(f\) peut être écrite comme\[f(x)=\frac{p(x)}{q(x)}=g(x)+\frac{r(x)}{q(x),} \nonumber \] si le degré de\(r(x)\) est inférieur au degré de\(q(x)\). Les valeurs de se\(f(x)\) rapprochent des valeurs de\(g(x)\) as\(x→±∞\). S'il s'\(g(x)\)agit d'une fonction linéaire, elle est connue sous le nom d'asymptote oblique.
- Déterminez\(f\) s'il présente des asymptotes verticales.
- Calculer\(f′.\) Trouvez tous les points critiques et déterminez les intervalles où\(f\) augmente et où\(f\) diminue. Déterminez\(f\) s'il présente des extrêmes locaux.
- Calculer\(f''.\) Déterminez les intervalles où\(f\) est concave vers le haut et où\(f\) est concave vers le bas. Utilisez ces informations pour déterminer s'il\(f\) possède des points d'inflexion. La dérivée seconde peut également être utilisée comme moyen alternatif pour déterminer ou vérifier\(f\) s'il y a un extremum local à un point critique.
Utilisons maintenant cette stratégie pour représenter graphiquement plusieurs fonctions différentes. Nous commençons par représenter graphiquement une fonction polynomiale.
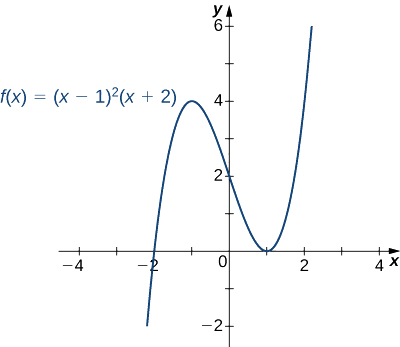
Esquissez un graphique de\(f(x)=(x−1)^2(x+2).\)
Solution
Étape 1 : Comme\(f\) il s'agit d'un polynôme, le domaine est l'ensemble de tous les nombres réels.
Étape 2 : Lorsque,\(x=0,\; f(x)=2.\) par conséquent, le\(y\) -intercept est\((0,2)\). Pour trouver les\(x\) -intercepts, nous devons résoudre l'équation\((x−1)^2(x+2)=0\), qui nous donne les\(x\) -intercepts\((1,0)\) et\((−2,0)\)
Étape 3 : Nous devons évaluer le comportement final de\(f.\) As\(x→∞, \;(x−1)^2→∞\) et\((x+2)→∞\). Par conséquent,\(\displaystyle \lim_{x→∞}f(x)=∞\).
Comme\(x→−∞, \;(x−1)^2→∞\) et\((x+2)→−∞\). Par conséquent,\(\displaystyle \lim_{x→-∞}f(x)=−∞\).
Pour obtenir encore plus d'informations sur le comportement final de\(f\), nous pouvons multiplier les facteurs de\(f\). Ce faisant, nous constatons que
\[f(x)=(x−1)^2(x+2)=x^3−3x+2. \nonumber \]
Puisque le terme principal de\(f\) est\(x^3\), nous concluons qu'il\(f\) se comporte\(y=x^3\) comme\(x→±∞.\)
Étape 4 : Comme il\(f\) s'agit d'une fonction polynomiale, elle ne possède aucune asymptote verticale.
Étape 5 : La première dérivée de\(f\) est
\[f′(x)=3x^2−3. \nonumber \]
Par conséquent,\(f\) a deux points critiques :\(x=1,−1.\) Divisez l'intervalle\((−∞,∞)\) en trois intervalles plus petits :\((−∞,−1), \;(−1,1)\), et\((1,∞)\). Ensuite, choisissez des points de test et\(x=−2, x=0\),\(x=2\) à partir de ces intervalles, évaluez le signe de\(f′(x)\) à chacun de ces points de test, comme indiqué dans le tableau suivant.
| Intervalle | Point d'essai | Signe de dérivé\(f'(x)=3x^2−3=3(x−1)(x+1)\) | Conclusion |
|---|---|---|---|
| \((−∞,−1)\) | \(x=−2\) | \ (f' (x) =3x^2−3=3 (x−1) (x+1) \) » style="text-align:center ; « >\((+)(−)(−)=+\) | \(f\)augmente |
| \((−1,1)\) | \(x=0\) | \ (f' (x) =3x^2−3=3 (x−1) (x+1) \) » style="text-align:center ; « >\((+)(−)(+)=−\) | \(f\)décroissant |
| \((1,∞)\) | \(x=2\) | \ (f' (x) =3x^2−3=3 (x−1) (x+1) \) » style="text-align:center ; « >\((+)(+)(+)=+\) | \(f\)augmente |
Dans le tableau, nous voyons qu'il\(f\) y a un maximum local à\(x=−1\) et un minimum local à\(x=1\). \(f(x)\)En évaluant à ces deux points, nous constatons que la valeur maximale locale est\(f(−1)=4\) et que la valeur minimale locale est\(f(1)=0.\)
Étape 6 : La deuxième dérivée de\(f\) est
\[f''(x)=6x. \nonumber \]
La dérivée seconde est nulle à\(x=0.\) Par conséquent, pour déterminer la concavité de\(f\), divisez l'intervalle\((−∞,∞)\) en intervalles plus petits\((−∞,0)\) et\((0,∞)\), choisissez des points de test\(x=−1\) et\(x=1\) pour déterminer la concavité de\(f\) sur chacun de ces intervalles plus petits comme indiqué dans le tableau suivant.
| Intervalle | Point d'essai | Signe de\(f''(x)=6x\) | Conclusion |
|---|---|---|---|
| \((−∞,0)\) | \(x=−1\) | \ (f « (x) =6x \) » style="text-align:center ; « >\(−\) | \(f\)est concave vers le bas. |
| \((0,∞)\) | \(x=1\) | \ (f « (x) =6x \) » style="text-align:center ; « >\(+\) | \(f\)est concave vers le haut. |
Nous notons que les informations du tableau précédent confirment le fait, constaté à l'étape\(5\), que f a un maximum local à\(x=−1\) et un minimum local à\(x=1\). En outre, les informations trouvées à l'étape\(5\), à savoir qu'elles\(f\) ont un maximum local\(x=−1\) et un minimum local à et à ces points\(x=1\), combinées\(f′(x)=0\) au fait que les\(f''\) modifications ne sont signées qu'à,\(x=0\) confirment les résultats trouvés à l'étape\(6\) sur concavité de\(f\).
En combinant ces informations, nous arrivons au graphique\(f(x)=(x−1)^2(x+2)\) présenté dans le graphique suivant.
Esquissez un graphique de\(f(x)=(x−1)^3(x+2).\)
- Allusion
-
\(f\)est un polynôme du quatrième degré.
- Réponse
-
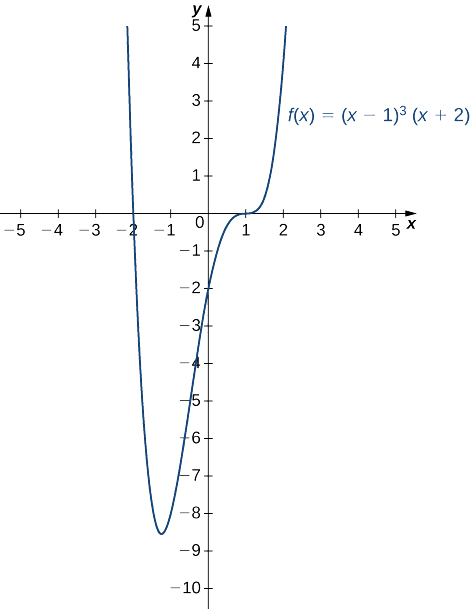
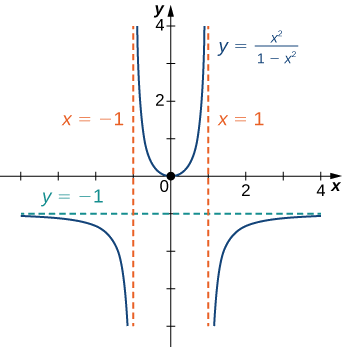
Esquissez le graphique de\(f(x)=\dfrac{x^2}{1−x^2}\).
Solution
Étape 1 : La fonction\(f\) est définie tant que le dénominateur n'est pas nul. Par conséquent, le domaine est l'ensemble de tous les nombres réels\(x\) sauf\(x=±1.\)
Étape 2 : Trouvez les interceptions. \(x=0,\)Si c'est\(f(x)=0\) le cas, une interception l'\(0\)est aussi. Si\(y=0\), alors\(\dfrac{x^2}{1−x^2}=0,\) ce qui implique\(x=0\). C'\((0,0)\)est donc la seule interception.
Étape 3 : Évaluez les limites à l'infini. Comme\(f\) il s'agit d'une fonction rationnelle, divisez le numérateur et le dénominateur par la plus grande puissance du dénominateur :\(x^2\) .Nous obtenons
\(\displaystyle \lim_{x→±∞}\frac{x^2}{1−x^2}=\lim_{x→±∞}\frac{1}{\frac{1}{x^2}−1}=−1.\)
Par conséquent,\(f\) possède une asymptote horizontale de\(y=−1\) as\(x→∞\) et\(x→−∞.\)
Étape 4 : Pour déterminer s'il\(f\) possède des asymptotes verticales, vérifiez d'abord si le dénominateur comporte des zéros. Nous trouvons que le dénominateur est zéro quand\(x=±1\). Pour déterminer si les lignes\(x=1\) ou\(x=−1\) sont des asymptotes verticales de\(f\), évaluez\(\displaystyle \lim_{x→1}f(x)\) et\(\displaystyle \lim_{x→−1}f(x)\). En examinant chaque limite unilatérale comme\(x→1,\) nous le voyons
\(\displaystyle \lim_{x→1^+}\frac{x^2}{1−x^2}=−∞\)et\(\displaystyle \lim_{x→1^−}\frac{x^2}{1−x^2}=∞.\)
De plus, en examinant chaque limite unilatérale,\(x→−1,\) nous constatons que
\(\displaystyle \lim_{x→−1^+}\frac{x^2}{1−x^2}=∞\)et\(\displaystyle \lim_{x→−1^−}\frac{x^2}{1−x^2}=−∞.\)
Étape 5 : Calculez la première dérivée :
\(f′(x)=\dfrac{(1−x^2)(2x)−x^2(−2x)}{\Big(1−x^2\Big)^2}=\dfrac{2x}{\Big(1−x^2\Big)^2}\).
Les points critiques se situent à des points\(x\) non définis\(f′(x)=0\) ou\(f′(x)\) non définis. Nous voyons que\(f′(x)=0\) lorsque\(x=0.\) La dérivée n'\(f′\)est pas indéfinie à aucun moment dans le domaine de\(f\). Cependant, ne\(x=±1\) sont pas du domaine de\(f\). Par conséquent, pour déterminer où\(f\) augmente et où\(f\) diminue, divisez l'intervalle\((−∞,∞)\) en quatre intervalles plus petits :\((−∞,−1), (−1,0), (0,1),\) et\((1,∞)\) choisissez un point de test dans chaque intervalle pour déterminer le signe de\(f′(x)\) dans chacun de ces intervalles. Les valeurs\(x=−2,\; x=−\frac{1}{2}, \;x=\frac{1}{2}\) et\(x=2\) sont de bons choix pour les points de test, comme indiqué dans le tableau suivant.
| Intervalle | Point d'essai | Signe de\(f′(x)=\frac{2x}{(1−x^2)^2}\) | Conclusion |
|---|---|---|---|
| \((−∞,−1)\) | \(x=−2\) | \ (f′ (x) = \ frac {2x} {(1−x^2) ^2} \) » style="text-align:center ; « >\(−/+=−\) | \(f\)est en baisse. |
| \((−1,0)\) | \(x=−1/2\) | \ (f′ (x) = \ frac {2x} {(1−x^2) ^2} \) » style="text-align:center ; « >\(−/+=−\) | \(f\)est en baisse. |
| \((0,1)\) | \(x=1/2\) | \ (f′ (x) = \ frac {2x} {(1−x^2) ^2} \) » style="text-align:center ; « >\(+/+=+\) | \(f\)augmente. |
| \((1,∞)\) | \(x=2\) | \ (f′ (x) = \ frac {2x} {(1−x^2) ^2} \) » style="text-align:center ; « >\(+/+=+\) | \(f\)augmente. |
À partir de cette analyse, nous concluons qu'il y\(f\) a un minimum local\(x=0\) égal mais aucun maximum local.
Étape 6 : Calculez la dérivée seconde :
\ [\ begin {align*} f « (x) &= \ frac {(1−x^2) ^2 (2) −2x (2 (1−x^2) (−2x))} {(1−x^2) ^4} \ \ [4 points]
&= \ frac {(1−x^2) [2 (1−x^2) +8x^2] {} \ Grand (1−x^2 \ Big) ^4} \ \ [4 points]
&= \ frac {2 (1−x^2) +8x^2} {\ Grand (1−x^2 \ Big) ^3} \ \ [4 points]
&= \ frac {6x^2+2} {\ Grand (1−x^2 \ Big) ^3}. \ end {align*} \]
Pour déterminer les intervalles où\(f\) est concave vers le haut et où\(f\) est concave vers le bas, nous devons d'abord trouver tous les points\(x\) où\(f''(x)=0\) ou n'\(f''(x)\)est pas défini. Puisque le numérateur\(6x^2+2≠0\) de n'importe quel n'\(x, f''(x)\)est jamais zéro. En outre, n'\(f''\)est pas indéfini pour quiconque\(x\) dans le domaine de\(f\). Cependant, comme indiqué précédemment, ne\(x=±1\) relèvent pas du domaine de\(f\). Par conséquent, pour déterminer la concavité de\(f\), nous divisons l'intervalle\((−∞,∞)\) en trois intervalles\((−∞,−1), \, (−1,1)\) plus petits et\((1,∞)\) choisissons un point de test dans chacun de ces intervalles pour évaluer le signe de\(f''(x)\). Les valeurs et\(x=2\) sont des points de test possibles\(x=−2, \;x=0\), comme indiqué dans le tableau suivant.
| Intervalle | Point d'essai | Signe de\(f''(x)=\frac{6x^2+2}{(1−x^2)^3}\) | Conclusion |
|---|---|---|---|
| \((−∞,−1)\) | \(x=−2\) | \ (f « (x) = \ frac {6x^2+2} {(1−x^2) ^3} \) » style="text-align:center ; « >\(+/−=−\) | \(f\)est concave vers le bas. |
| \((−1,1)\) | \(x=0\) | \ (f « (x) = \ frac {6x^2+2} {(1−x^2) ^3} \) » style="text-align:center ; « >\(+/+=+\) | \(f\)est concave vers le haut |
| \((1,∞)\) | \(x=2\) | \ (f « (x) = \ frac {6x^2+2} {(1−x^2) ^3} \) » style="text-align:center ; « >\(+/−=−\) | \(f\)est concave vers le bas. |
En combinant toutes ces informations, nous arrivons au graphique\(f\) ci-dessous. Notez que, bien que la concavité\(f\) change à\(x=−1\) et\(x=1\), il n'y a aucun point d'inflexion à aucun de ces endroits car il n'\(f\)est pas continu à\(x=−1\) ou\(x=1.\)
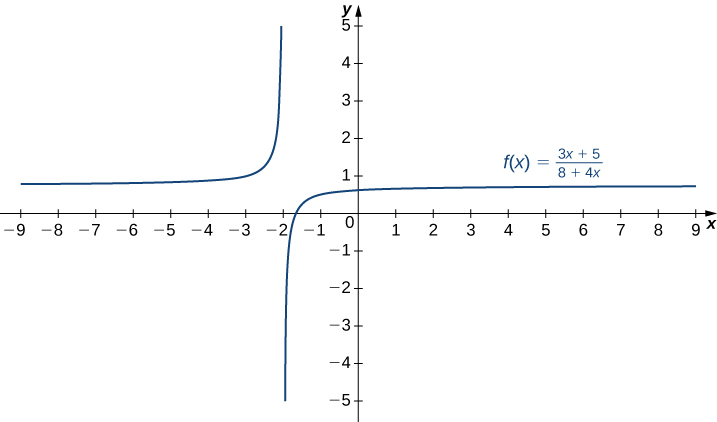
Esquissez un graphique de\(f(x)=\dfrac{3x+5}{8+4x}.\)
- Allusion
-
Une ligne\(y=L\) est une asymptote horizontale indiquant\(f\) si la limite est\(x→∞\) ou si la limite\(f(x)\) est\(x→−∞\) égale à\(L\). Une ligne\(x=a\) est une asymptote verticale si au moins l'une des limites unilatérales de\(x→a\) est\(f\) telle quelle\(∞\) ou\(−∞.\)
- Réponse
-
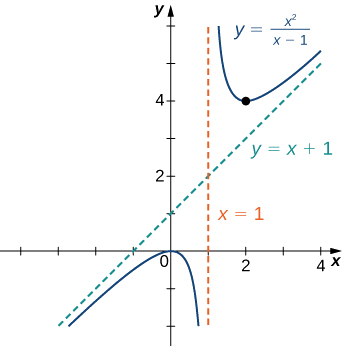
Esquissez le graphique de\(f(x)=\dfrac{x^2}{x−1}\)
Solution
Étape 1 : Le domaine de\(f\) est l'ensemble de tous les nombres réels\(x\) sauf\(x=1.\)
Étape 2 : Trouvez les interceptions. Nous pouvons le voir\(x=0, \,f(x)=0,\) alors que\((0,0)\) c'est la seule interception.
Étape 3 : Évaluez les limites à l'infini. Puisque le degré du numérateur est supérieur d'un au degré du dénominateur,\(f\) doit avoir une asymptote oblique. Pour trouver l'asymptote oblique, utilisez la division longue des polynômes pour écrire
\(f(x)=\dfrac{x^2}{x−1}=x+1+\dfrac{1}{x−1}\).
\(\dfrac{1}{x−1}→0\)Puisque l'on\(x→±∞, f(x)\) s'approche de la ligne\(y=x+1\) comme\(x→±∞\). La ligne\(y=x+1\) est une asymptote oblique pour\(f\).
Étape 4 : Pour vérifier la présence d'asymptotes verticales, regardez où le dénominateur est zéro. Ici, le dénominateur est nul.\(x=1.\) Si l'on considère les deux limites unilatérales, comme\(x→1,\) on le trouve
\(\displaystyle \lim_{x→1^+}\frac{x^2}{x−1}=∞\)et\(\displaystyle \lim_{x→1^−}\frac{x^2}{x−1}=−∞.\)
Par conséquent,\(x=1\) est une asymptote verticale, et nous avons déterminé le comportement de l'\(x\)approche\(f\) as\(1\) par la droite et la gauche.
Étape 5 : Calculez la dérivée première :
\(f′(x)=\dfrac{(x−1)(2x)−x^2(1)}{(x−1)^2}=\dfrac{x^2−2x}{(x−1)^2}.\)
Nous avons\(f′(x)=0\) quand\(x^2−2x=x(x−2)=0\). Par conséquent,\(x=0\) et\(x=2\) sont des points critiques. Comme\(f\) il n'est pas défini à\(x=1\), nous devons diviser l'intervalle\((−∞,∞)\) en intervalles plus petits\((−∞,0), (0,1), (1,2),\) et\((2,∞)\) choisir un point de test\(f′(x)\) dans chaque intervalle pour évaluer le signe de chacun de ces intervalles plus petits. Par exemple\(x=−1, x=\frac{1}{2}, x=\frac{3}{2}\), supposons et\(x=3\) soyez les points de test comme indiqué dans le tableau suivant.
| Intervalle | Point d'essai | Signe de\(f'(x)=\dfrac{x^2−2x}{(x−1)^2}\) | Conclusion |
|---|---|---|---|
| \((−∞,0)\) | \(x=−1\) | \ (f' (x) = \ dfrac {x^2−2x} {(x−1) ^2} \) » validation des données ="top"> (−) (−) /+=+ | \(f\)augmente. |
| \((0,1)\) | \(x=1/2\) | \ (f' (x) = \ dfrac {x^2−2x} {(x−1) ^2} \) » validation des données ="top"> (+) (−) /+=− | \(f\)est en baisse. |
| \((1,2)\) | \(x=3/2\) | \ (f' (x) = \ dfrac {x^2−2x} {(x−1) ^2} \) » validation des données ="top"> (+) (−) /+=− | \(f\)est en baisse. |
| \((2,∞)\) | \(x=3\) | \ (f' (x) = \ dfrac {x^2−2x} {(x−1) ^2} \) » validation des données ="top"> (+) (+) /+=+ | \(f\)augmente. |
À partir de ce tableau, nous voyons qu'il y\(f\) a un maximum local à\(x=0\) et un minimum local à\(x=2\). La valeur de\(f\) au maximum local est\(f(0)=0\) et la valeur de\(f\) au minimum local est\(f(2)=4\). Par conséquent,\((0,0)\) et\((2,4)\) sont des points importants sur le graphique.
Étape 6. Calculez la dérivée seconde :
\ [\ begin {align*} f « (x) &= \ frac {(x−1) ^2 (2x−2) −2 (x−1) (x^2−2x)} {(x−1) ^4} \ \ [4 points]
&= \ frac {2 (x−1) [(x−1) ^2− (x−1) ^2− (x^2−2x)]} {(x−1) ^2− (x−2 ×)]} {(x−1) ^2− (x−2 ×)]} {(x−1) 1) ^4} \ \ [4 points]
&= \ frac {2 [x^2-2x+1−x^2+2x]} {(x−1) ^3} \ \ [4 points]
&= \ frac {2} {(x−1) ^3}. \ end {align*} \]
Nous voyons que ce n'\(f''(x)\)est jamais nul ou indéfini\(x\) dans le domaine de\(f\). Comme\(f\) il n'est pas défini à\(x=1\), pour vérifier la concavité\((1,∞)\), il suffit de\((−∞,∞)\) diviser l'intervalle en deux intervalles\((−∞,1)\) plus petits et de choisir un point de test\(f''(x)\) dans chaque intervalle pour évaluer le signe de chacun de ces intervalles. Les valeurs\(x=0\) et\(x=2\) sont des points de test possibles, comme indiqué dans le tableau suivant.
| Intervalle | Point d'essai | Signe de\(f''(x)=\dfrac{2}{(x−1)^3}\) | Conclusion |
|---|---|---|---|
| \((−∞,1)\) | \(x=0\) | \ (f « (x) = \ dfrac {2} {(x−1) ^3} \) » style="text-align:center ; « >\(+/−=−\) | \(f\)est concave vers le bas. |
| \((1,∞)\) | \(x=2\) | \ (f « (x) = \ dfrac {2} {(x−1) ^3} \) » style="text-align:center ; « >\(+/+=+\) | \(f\)est concave vers le haut |
À partir des informations recueillies, nous arrivons au graphique suivant pour\(f.\)
Trouvez l'asymptote oblique pour\(f(x)=\dfrac{3x^3−2x+1}{2x^2−4}\).
- Allusion
-
Utilisez une division longue des polynômes.
- Réponse
-
\(y=\frac{3}{2}x\)
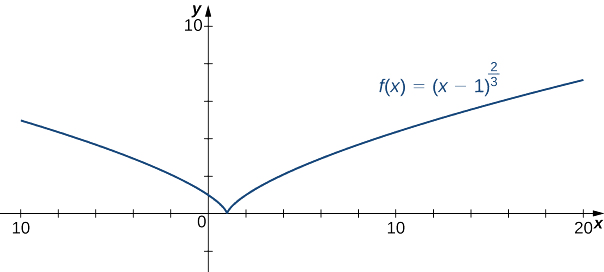
Esquissez un graphique de\(f(x)=(x−1)^{2/3}\)
Solution
Étape 1 : Puisque la fonction cube-root est définie pour tous les nombres réels\(x\) et\((x−1)^{2/3}=(\sqrt[3]{x−1})^2\) que le domaine de\(f\) est composé de tous les nombres réels.
Étape 2 : Pour trouver le\(y\) -intercept, évaluez\(f(0)\). Puisque\(f(0)=1,\) le\(y\) -intercept est\((0,1)\). Pour trouver le\(x\) -intercept, résolvez\((x−1)^{2/3}=0\). La solution de cette équation est\(x=1\), donc le\(x\) -intercept est\((1,0).\)
Étape 3 : Puisque\(\displaystyle \lim_{x→±∞}(x−1)^{2/3}=∞,\) la fonction continue de croître sans limites au fur\(x→∞\) et à mesure\(x→−∞.\)
Étape 4 : La fonction ne comporte aucune asymptote verticale.
Étape 5 : Pour déterminer où\(f\) augmente ou diminue, calculez\(f′.\) Nous trouvons
\[f′(x)=\frac{2}{3}(x−1)^{−1/3}=\frac{2}{3(x−1)^{1/3}} \nonumber \]
Cette fonction n'est nulle part nulle part, mais elle n'est pas définie lorsque,\(x=1.\) par conséquent, le seul point critique est de\(x=1.\)\((−∞,∞)\) diviser l'intervalle en intervalles\((−∞,1)\) plus petits et de choisir des points de test dans chacun de ces intervalles pour déterminer le signe de\(f′(x)\) dans chacun de ces intervalles\((1,∞)\) intervalles plus petits. \(x=2\)Soit\(x=0\) les points de test comme indiqué dans le tableau suivant.
| Intervalle | Point d'essai | Signe de\(f′(x)=\frac{2}{3(x−1)^{1/3}}\) | Conclusion |
|---|---|---|---|
| \((−∞,1)\) | \(x=0\) | \ (f′ (x) = \ frac {2} {3 (x−1) ^ {1/3}} \) » style="text-align:center ; « >\(+/−=−\) | \(f\)est décroissant |
| \((1,∞)\) | \(x=2\) | \ (f′ (x) = \ frac {2} {3 (x−1) ^ {1/3}} \) » style="text-align:center ; « >\(+/+=+\) | \(f\)augmente |
Nous concluons qu'il\(f\) y a un minimum local à\(x=1\). \(f\)En évaluant à\(x=1\), nous constatons que la valeur de\(f\) au minimum local est nulle. Notez que ce n'\(f′(1)\)est pas défini, donc pour déterminer le comportement de la fonction à ce point critique, nous devons examiner.\(\displaystyle \lim_{x→1}f′(x).\) En regardant les limites unilatérales, nous avons
\[\lim_{x→1^+}\frac{2}{3(x−1)^{1/3}}=∞\text{ and } \lim_{x→1^−}\frac{2}{3(x−1)^{1/3}}=−∞.\nonumber \]
Par conséquent,\(f\) a une pointe à\(x=1.\)
Étape 6 : Pour déterminer la concavité, nous calculons la dérivée seconde de\(f:\)
\[f''(x)=−\dfrac{2}{9}(x−1)^{−4/3}=\dfrac{−2}{9(x−1)^{4/3}}. \nonumber \]
Nous constatons que cela\(f''(x)\) est défini pour tous\(x\), mais qu'il n'est pas défini quand\(x=1\). Divisez donc l'intervalle\((−∞,∞)\) en intervalles plus petits\((−∞,1)\) et\((1,∞)\) choisissez des points de test pour évaluer le signe\(f''(x)\) de chacun de ces intervalles. Comme nous l'avons fait précédemment,\(x=0\) considérez\(x=2\) comme des points de test comme indiqué dans le tableau suivant.
| Intervalle | Point d'essai | Signe de\(f''(x)=\dfrac{−2}{9(x−1)^{4/3}}\) | Conclusion |
|---|---|---|---|
| \((−∞,1)\) | \(x=0\) | \ (f « (x) = \ dfrac {−2} {9 (x−1) ^ {4/3}} \) » style="text-align:center ; « >\(−/+=−\) | \(f\)est concave vers le bas |
| \((1,∞)\) | \(x=2\) | \ (f « (x) = \ dfrac {−2} {9 (x−1) ^ {4/3}} \) » style="text-align:center ; « >\(−/+=−\) | \(f\)est concave vers le bas |
D'après ce tableau, nous concluons que\(f\) c'est concave partout. En combinant toutes ces informations, nous arrivons au graphique suivant pour\(f\).
Réfléchissez à la fonction\(f(x)=5−x^{2/3}\). Déterminez le point du graphique où se trouve une cuspide. Déterminez le comportement final de\(f\).
- Allusion
-
Une fonction\(f\) a une pointe à un point\(a\) si\(f(a)\) elle existe, si elle n'\(f'(a)\)est pas définie, si l'une des limites unilatérales\(f'(x)\) est telle que\(x→a\)\(+∞\), et l'autre limite unilatérale est\(−∞.\)
- Réponse
-
La fonction\(f\) a un point critique à\((0,5)\), depuis\(\displaystyle \lim_{x→0^−}f′(x)=∞\) et\(\displaystyle \lim_{x→0^+}f′(x)=−∞\). Pour le comportement final,\(\displaystyle \lim_{x→±∞}f(x)=−∞.\)
Concepts clés
- La limite de\(f(x)\) est égale\(L\) à\(x→∞\) (ou comme\(x→−∞)\) si les valeurs\(f(x)\) devenaient arbitrairement proches de\(L\) celles qui\(x\) devenaient suffisamment grandes).
- La limite de\(f(x)\) est\(∞\) comme\(x→∞\) si\(f(x)\) elle devenait arbitrairement grande lorsqu'\(x\)elle devenait suffisamment grande. La limite de\(f(x)\) est\(−∞\) comme\(x→∞\) si\(|f(x)|\) elle devenait arbitrairement grande au fur\(f(x)<0\) et à mesure qu'\(x\)elle devenait suffisamment grande. Nous pouvons définir la limite des\(x\) approches\(f(x)\) de la\(−∞\) même manière.
- Pour une fonction polynomiale\(p(x)=a_nx^n+a_{n−1}x^{n−1}+…+a_1x+a_0,\) où\(a_n≠0\), le comportement final est déterminé par le terme principal\(a_nx^n\). S'il\(n≠0, p(x)\) approche\(∞\) ou\(−∞\) à chaque extrémité.
- Pour une fonction rationnelle,\(f(x)=\dfrac{p(x)}{q(x),}\) le comportement final est déterminé par la relation entre le degré\(p\) et le degré de\(q\). Si le degré de\(p\) est inférieur au degré de\(q\), la ligne\(y=0\) est une asymptote horizontale pour\(f\). Si le degré de\(p\) est égal au degré de\(q\), alors la droite\(y=\dfrac{a_n}{b_n}\) est une asymptote horizontale, où\(a_n\) et\(b_n\) sont les principaux coefficients de\(p\) et\(q\), respectivement. Si le degré de\(p\) est supérieur au degré de\(q\), alors\(f\) approche\(∞\) ou\(−∞\) à chaque extrémité.
Lexique
- comportement final
- le comportement d'une fonction en tant que\(x→∞\) et\(x→−∞\)
- asymptote horizontale
- si\(\displaystyle \lim_{x→∞}f(x)=L\) ou\(\displaystyle \lim_{x→−∞}f(x)=L\), alors\(y=L\) est une asymptote horizontale de\(f\)
- limite infinie à l'infini
- une fonction qui devient arbitrairement grande au\(x\) fur et à mesure
- limite à l'infini
- une fonction qui s'approche d'une valeur limite\(L\) lorsqu'\(x\)elle devient grande
- asymptote oblique
- la ligne\(y=mx+b\) si elle s'en\(f(x)\) rapproche\(x→∞\) ou\( x→−∞\)


