2.5E : Exercices pour la section 2.5

Last updated
Save as PDF

Page ID: 198027

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Dans les exercices 1 à 4, écrivez la$ ε − δ$ définition appropriée pour chacune des déclarations données.

1)$\displaystyle \lim_{x →a}f(x)=N$

2)$\displaystyle \lim_{t →b}g(t)=M$

Réponse: Pour chacun$ ε >0$, il existe un$ δ >0$, de sorte que si$0 <|t −b| < δ$, alors$|g(t) −M| < ε$

3)$\displaystyle \lim_{x →c}h(x)=L$

4)$\displaystyle \lim_{x →a} φ(x)=A$

Réponse: Pour chacun$ ε >0$, il existe un$ δ >0$, de sorte que si$0 <|x −a| < δ$, alors$| φ(x) −A| < ε$

Le graphique suivant de la fonction$f$ satisfait$\displaystyle \lim_{x →2}f(x)=2$. Dans les exercices suivants, déterminez une valeur$ δ >0$ qui satisfait chaque instruction.

Une fonction dessinée dans le premier quadrant pour x 0. Il s'agit d'une fonction ascendante concave croissante, dont les points sont approximativement (0,0), (1, ,5), (2,2) et (3,4)." style="width: 417px; height: 422px;" width="417px" height="422px" src="https://math.libretexts.org/@api/dek...02_05_204.jpeg">

5) Si$0 <|x −2| < δ$, alors$|f(x) −2| <1$.

6) Si$0 <|x −2| < δ$, alors$|f(x) −2| <0.5$.

Réponse: $ δ ≤0.25$

Le graphique suivant de la fonction$f$ satisfait$\displaystyle \lim_{x →3}f(x)= −1$. Dans les exercices suivants, déterminez une valeur$ δ >0$ qui satisfait chaque instruction.

Un graphe d'une fonction linéaire décroissante, avec des points (0,2), (1,1), (2,0), (3, -1), (4, -2), etc. pour x = 0." style="width: 417px; height: 422px;" width="417px" height="422px" src="https://math.libretexts.org/@api/dek...02_05_205.jpeg">

7) Si$0 <|x −3| < δ$, alors$|f(x)+1| <1$.

8) Si$0 <|x −3| < δ$, alors$|f(x)+1| <2$.

Réponse: $ δ ≤2$

Le graphique suivant de la fonction$f$ satisfait$\displaystyle \lim_{x →3}f(x)=2$. Dans les exercices suivants, pour chaque valeur de$ ε$, trouvez une valeur$ δ >0$ telle que la définition précise de la limite soit vraie.

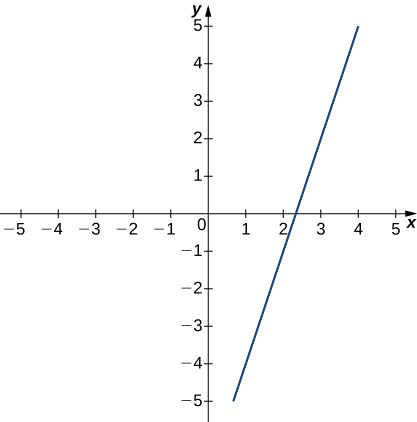
$Graphique d'une fonction linéaire croissante coupant l'axe x à environ (2,25, 0) et passant par les points (3,2) et, approximativement, (1, -5) et (4,5).$

9)$ ε=1.5$

10)$ ε=3$

Réponse: $ δ ≤1$

[T] Dans les exercices 11 à 12, utilisez une calculatrice graphique pour trouver un nombre$ δ$ tel que les affirmations soient vraies.

11)$\left|\sin(2x) −\frac{1}{2}\right| <0.1$, chaque fois que$\left|x −\frac{ π}{12}\right| < δ$

12)$\left|\sqrt{x −4} −2\right| <0.1$, chaque fois que$|x −8| < δ$

Réponse: $ δ <0.3900$

Dans les exercices 13 à 17, utilisez la définition précise de la limite pour prouver les limites données.

13)$\displaystyle \lim_{x →2}\,(5x+8)=18$

(14)$\displaystyle \lim_{x →3}\frac{x^2 −9}{x −3}=6$

Réponse: Laissez$ δ= ε$. Si$0 <|x −3| < ε$, alors$\left|\dfrac{x^2 −9}{x −3} - 6\right| = \left|\dfrac{(x+3)(x −3)}{x −3} - 6\right| = |x+3 −6|=|x −3| < ε$.

15)$\displaystyle \lim_{x →2}\frac{2x^2 −3x −2}{x −2}=5$

16)$\displaystyle \lim_{x →0}x^4=0$

Réponse: Laissez$ δ=\sqrt[4]{ ε}$. Si$0 <|x| <\sqrt[4]{ ε}$, alors$\left|x^4-0\right|=x^4 < ε$.

17)$\displaystyle \lim_{x →2}\,(x^2+2x)=8$

Dans les exercices 18 à 20, utilisez la définition précise de la limite pour prouver les limites unilatérales données.

18)$\displaystyle \lim_{x →5^ −}\sqrt{5 −x}=0$

Réponse: Laissez$ δ= ε^2$. Si$- ε^2 < x - 5 < 0,$ nous pouvons multiplier par$-1$ pour obtenir$0 <5-x < ε^2.$
Then$\left|\sqrt{5 −x} - 0\right|=\sqrt{5 −x} < \sqrt{ ε^2} = ε$.

19)$\displaystyle \lim_{x →0^+}f(x)= −2$, où$f(x)=\begin{cases}8x −3, & \text{if }x <0\\4x −2, & \text{if }x ≥0\end{cases}$.

20)$\displaystyle \lim_{x →1^ −}f(x)=3$, où$f(x)=\begin{cases}5x −2, & \text{if }x <1\\7x −1, & \text{if }x ≥1\end{cases}$.

Réponse: Laissez$ δ= ε/5$. Si$ − ε/5 < x - 1 <0,$ on peut multiplier par$-1$ pour obtenir Then$0 <1-x < ε/5.$
$|f(x) −3|=|5x-2-3| = |5x −5| = 5(1-x),$ depuis$x <1$ ici.
Et$5(1-x) < 5( ε/5) = ε$.

Dans les exercices 21 à 23, utilisez la définition précise de la limite pour prouver les limites infinies données.

(21)$\displaystyle \lim_{x →0}\frac{1}{x^2}= ∞$

22)$\displaystyle \lim_{x → −1}\frac{3}{(x+1)^2}= ∞$

Réponse: Laissez$ δ=\sqrt{\frac{3}{N}}$. Si$0 <|x+1| <\sqrt{\frac{3}{N}}$, alors$f(x)=\frac{3}{(x+1)^2} >N$.

23)$\displaystyle \lim_{x →2} −\frac{1}{(x −2)^2}= − ∞$

24) Un ingénieur utilise une machine pour découper un carré plat d'aérogel de surface$144 \,\text{cm}^2$. S'il existe une tolérance d'erreur maximale dans la zone de$8 \,\text{cm}^2$, avec quelle précision l'ingénieur doit-il couper sur le côté, en supposant que tous les côtés ont la même longueur ? Comment ces chiffres sont-ils liés à$ δ$$ ε$,$a$, et$L$ ?

Réponse: $0.033 \text{ cm}, \, ε=8,\, δ=0.33,\,a=12,\,L=144$

25) Utilisez la définition précise de la limite pour prouver que la limite suivante n'existe pas :$\displaystyle \lim_{x →1}\frac{|x −1|}{x −1}.$

26) À l'aide de définitions précises des limites, prouvez que$\displaystyle \lim_{x →0}f(x)$ cela n'existe pas, étant donné que$f(x)$ c'est la fonction de plafond. (Conseil : Essayez-en un$ δ <1$.)

Réponse: Les réponses peuvent très bien.

27) À l'aide de définitions précises des limites, prouvez que$\displaystyle \lim_{x →0}f(x)$ cela n'existe pas :$f(x)=\begin{cases}1, & \text{if }x\text{ is rational}\\0, & \text{if }x\text{ is irrational}\end{cases}$. (Conseil : réfléchissez à la façon dont vous pouvez toujours choisir un nombre rationnel$0 <d$, >

28) À l'aide de définitions précises des limites, déterminez$\displaystyle \lim_{x →0}f(x)$ pour$f(x)=\begin{cases}x, & \text{if }x\text{ is rational}\\0, & \text{if }x\text{ is irrational}\end{cases}$. (Indice : Divisez en deux cas,$x$ rationnel et$x$ irrationnel.)

Réponse: $0$

29) À l'aide de la fonction de l'exercice précédent, utilisez la définition précise des limites pour montrer que cela$\displaystyle \lim_{x →a}f(x)$ n'existe pas pour$a ≠0$

Pour les exercices 30 à 32, supposons que cela existe$\displaystyle \lim_{x →a}f(x)=L$ et que$\displaystyle \lim_{x →a}g(x)=M$ les deux existent. Utilisez la définition précise des limites pour prouver les lois limites suivantes :

30)$\displaystyle \lim_{x →a}(f(x) −g(x))=L −M$

Réponse: $f(x) −g(x)=f(x)+( −1)g(x)$

31)$\displaystyle \lim_{x →a}[cf(x)]=cL$ pour toute constante réelle$c$ (Conseil : considérez deux cas :$c=0$ et$c ≠0$.)

32)$\displaystyle \lim_{x →a}[f(x)g(x)]=LM$. (Astuce :$|f(x)g(x) −LM|= |f(x)g(x) −f(x)M +f(x)M −LM| ≤|f(x)||g(x) −M| +|M||f(x) −L|.)$

Réponse: Les réponses peuvent varier.