13.3 : Séquences géométriques
- Page ID
- 194937
- Trouvez le ratio commun pour une séquence géométrique.
- Répertoriez les termes d'une séquence géométrique.
- Utilisez une formule récursive pour une séquence géométrique.
- Utilisez une formule explicite pour une séquence géométrique.
De nombreux emplois offrent une augmentation annuelle du coût de la vie afin de maintenir les salaires en phase avec l'inflation. Supposons, par exemple, qu'un jeune diplômé trouve un poste de directeur des ventes gagnant un salaire annuel de\($26,000\). On lui promet une augmentation du\(2\%\) coût de la vie chaque année. Son salaire annuel pour une année donnée peut être trouvé en multipliant son salaire de l'année précédente par\(102\%\). Son salaire sera au\($26,520\) bout d'un an, au\($27,050.40\) bout de deux ans, au\($27,591.41\) bout de trois ans, et ainsi de suite. Lorsqu'un salaire augmente à un taux constant chaque année, il augmente d'un facteur constant. Dans cette section, nous allons passer en revue les séquences qui se développent de cette manière.
Trouver des ratios communs
Les valeurs salariales annuelles décrites forment une séquence géométrique car elles changent d'un facteur constant chaque année. Chaque terme d'une séquence géométrique augmente ou diminue selon un facteur constant appelé ratio commun. La séquence ci-dessous est un exemple de séquence géométrique car chaque terme augmente d'un facteur constant de 6. En multipliant n'importe quel terme de la séquence par le rapport commun 6, on obtient le terme suivant.

Une séquence géométrique est une séquence dans laquelle tout terme divisé par le terme précédent est une constante. Cette constante est appelée ratio commun de la séquence. Le ratio commun peut être trouvé en divisant n'importe quel terme de la séquence par le terme précédent. Si\(a_1\) est le terme initial d'une séquence géométrique et\(r\) est le ratio commun, la séquence sera
\[\{a_1, a_1r,a_1r^2,a_1r^3,...\} .\]
- Divisez chaque terme par le terme précédent.
- Comparez les quotients. S'ils sont identiques, il existe un ratio commun et la séquence est géométrique.
La séquence est-elle géométrique ? Si c'est le cas, trouvez le ratio commun.
- \(1\),\(2\),\(4\),\(8\),\(16\),...
- \(48\),\(12\),\(4\),\(2\),...
Solution
Divisez chaque terme par le terme précédent pour déterminer s'il existe un ratio commun.
- \(\dfrac{2}{1}=2\)\(\dfrac{4}{2}=2\)\(\dfrac{8}{4}=2\)\(\dfrac{16}{8}=2\)
La séquence est géométrique car il existe un ratio commun. Le ratio commun est\(2\).
- \(\dfrac{12}{48}=\dfrac{1}{4}\)\(\dfrac{4}{12}=\dfrac{1}{3}\)\(\dfrac{2}{4}=\dfrac{1}{2}\)
La séquence n'est pas géométrique car il n'existe pas de ratio commun.
Analyse
Le graphique de chaque séquence est illustré sur la figure\(\PageIndex{1}\). Il ressort des graphiques que (a) et (b) apparaissent tous deux sous la forme du graphe d'une fonction exponentielle dans cette fenêtre de visualisation. Cependant, nous savons que (a) est géométrique et donc cette interprétation est valable, mais (b) ne l'est pas.
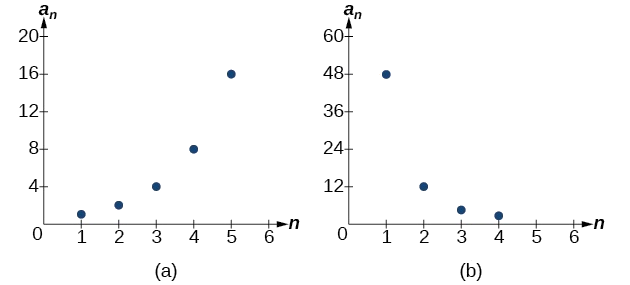
Figurine\(\PageIndex{1}\)
Si on vous dit qu'une séquence est géométrique, devez-vous diviser chaque terme par le terme précédent pour trouver le ratio commun ?
Non Si vous savez que la séquence est géométrique, vous pouvez choisir n'importe quel terme de la séquence et le diviser par le terme précédent pour trouver le ratio commun.
La séquence est-elle géométrique ? Si c'est le cas, trouvez le ratio commun.
\(5\),\(10\),\(15\),\(20\),...
- Réponse
-
La séquence n'est pas géométrique car\(\dfrac{10}{5}≠\dfrac{15}{10}\)
La séquence est-elle géométrique ? Si c'est le cas, trouvez le ratio commun.
\(100\),\(20\),\(4\),\(\dfrac{4}{5}\),...
- Réponse
-
La séquence est géométrique. Le ratio commun est\(\dfrac{1}{5}\)
Écrire des termes de séquences géométriques
Maintenant que nous pouvons identifier une séquence géométrique, nous allons apprendre à trouver les termes d'une séquence géométrique si l'on nous donne le premier terme et le ratio commun. Les termes d'une séquence géométrique peuvent être trouvés en commençant par le premier terme et en les multipliant par le ratio commun à plusieurs reprises. Par exemple, si le premier terme d'une séquence géométrique est\(a_1=−2\) et que le ratio commun est\(r=4\), nous pouvons trouver les termes suivants en multipliant\(−2⋅4\) pour obtenir,\(−8\) puis en multipliant le résultat\(−8⋅4\) pour obtenir\(−32\) et ainsi de suite.
\[\begin{align*} a_1 &= −2 \\ a_2 &= (−2⋅4)=−8 \\ a_3 &= (−8⋅4)=−32 \\ a_4 &= (−32⋅4)=128 \end{align*}\]
Les quatre premiers termes sont\(\{–2, –8, –32, –128\}\).
- Multipliez le terme initial par le ratio commun pour trouver le terme suivant,\(a_2\).\(a_1\)
- Répétez le processus en utilisant\(a_n=a_2\) pour rechercher,\(a_3\) puis en utilisant\(a_3\) pour rechercher\(a_4\), jusqu'à ce que les quatre termes soient identifiés.
- Écrivez les termes séparés par des termes communs entre crochets.
Répertoriez les quatre premiers termes de la séquence géométrique avec\(a_1=5\) et\(r=–2\).
Solution
Multipliez\(a_1\) par\(−2\) pour trouver\(a_2\). Répétez le processus en utilisant\(a_2\) pour rechercher\(a_3\), etc.
\[\begin{align*} a_1 &= 5 \\ a_2 &= −2a_1=−10 \\ a_3 &= −2a_2=20 \\ a_4 &= −2a_3=−40 \end{align*}\]
Les quatre premiers termes sont\(\{5,–10,20,–40\}\).
Répertoriez les cinq premiers termes de la séquence géométrique avec\(a_1=18\) et\(r=\dfrac{1}{3}\).
- Réponse
-
\(\left \{18, 6, 2, \dfrac{2}{3}, \dfrac{2}{9} \right \} \)
Utilisation de formules récursives pour les séquences géométriques
Une formule récursive nous permet de trouver n'importe quel terme d'une séquence géométrique en utilisant le terme précédent. Chaque terme est le produit du ratio commun et du terme précédent. Supposons, par exemple, que le ratio commun soit\(9\). Ensuite, chaque terme correspond à neuf fois le terme précédent. Comme pour toute formule récursive, le terme initial doit être indiqué.
La formule récursive pour une séquence géométrique avec un rapport r et un premier terme communs\(a_1\) est
\[a_n=ra_{n−1},\;\;\; n≥2\]
- Indiquez la durée initiale.
- Trouvez le ratio commun en divisant n'importe quel terme par le terme précédent.
- Substituez le ratio commun dans la formule récursive pour une séquence géométrique.
Écrivez une formule récursive pour la séquence géométrique suivante.
\(\{6, 9, 13.5, 20.25, ...\} \nonumber\)
Solution
Le premier terme est donné sous la forme\(6\). Le ratio commun peut être trouvé en divisant le deuxième terme par le premier terme.
\(r=\dfrac{9}{6}=1.5 \nonumber\)
Substituez le ratio commun dans la formule récursive pour les séquences géométriques et définissez\(a_1\).
\[\begin{align*} a_n &= ra_{n−1} \\ a_n &= 1.5a_{n−1} \text{ for }n≥2 \\ a_1 &= 6 \end{align*}\]
Analyse
La séquence de points de données suit un schéma exponentiel. Le ratio commun est également la base d'une fonction exponentielle, comme le montre la figure\(\PageIndex{2}\).
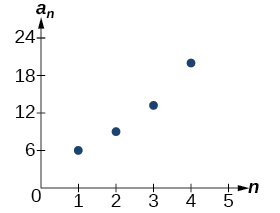
Figurine\(\PageIndex{2}\)
Faut-il diviser le deuxième terme par le premier terme pour trouver le ratio commun ?
Non Nous pouvons diviser n'importe quel terme de la séquence par le terme précédent. Il est toutefois plus courant de diviser le deuxième terme par le premier terme, car c'est souvent la méthode la plus simple pour trouver le ratio commun.
Écrivez une formule récursive pour la séquence géométrique suivante.
\(\{2, 43, 89, 1627, ...\}\)
- Réponse
-
\(\begin{align*}a_1 &= 2 \\ a_n &= \dfrac{2}{3}a_{n−1} \text{ for }n≥2 \end{align*}\)
Utilisation de formules explicites pour les séquences géométriques
Comme une séquence géométrique est une fonction exponentielle dont le domaine est l'ensemble des entiers positifs et que le ratio commun est la base de la fonction, nous pouvons écrire des formules explicites qui nous permettent de trouver des termes particuliers.
\[a_n=a_1r^{n−1}\]
Jetons un coup d'œil à la séquence\(\{18, 36, 72, 144, 288, ...\}\). Il s'agit d'une séquence géométrique avec un ratio commun de\(2\) et une fonction exponentielle avec une base de\(2\). Une formule explicite pour cette séquence est
\(a_n=18·2^{n−1}\)
Le graphique de la séquence est illustré sur la figure\(\PageIndex{3}\).
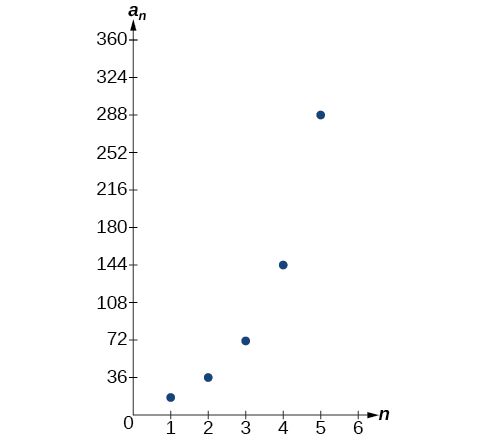
Figurine\(\PageIndex{3}\)
Le\(n^{th}\) terme d'une séquence géométrique est donné par la formule explicite :
\[a_n=a_1r^{n−1}\]
Étant donné une séquence géométrique avec\(a_1=3\) et\(a_4=24\), trouvez\(a_2\).
Solution
La séquence peut être écrite en termes de terme initial et de ratio commun\(r\).
\(3\),\(3r\),\(3r^2\),\(3r^3\),...
Trouvez le ratio commun en utilisant le quatrième terme donné.
\[\begin{align*} a_n&=a_1r^{n-1} \\ a_4&=3r^3 \qquad \text{Write the fourth term of sequence in terms of }\alpha_1 \text{ and } r \\ 24&=3r^3 \qquad \text{Substitute }24 \text{ for }a_4 \\ 8&=r^3 \qquad \text{Divide} \\ r&=2 \qquad \text{Solve for the common ratio} \end{align*}\]
Trouvez le deuxième terme en multipliant le premier terme par le ratio commun.
\[\begin{align*} a_2 &= 2 \\ a_1 &= 2(3) \\ & = 6 \end{align*}\]
Analyse
Le ratio commun est multiplié par le premier terme une fois pour trouver le deuxième terme, deux fois pour trouver le troisième terme, trois fois pour trouver le quatrième terme, etc. Le dixième terme peut être trouvé en multipliant le premier terme par le rapport commun neuf fois ou en multipliant par le ratio commun porté à la neuvième puissance.
Étant donné une séquence géométrique avec\(a_2=4\) et\(2a_3=32\), trouvez\(a_6\).
- Réponse
-
\(a_6=16,384\)
Écrivez une formule explicite pour le nième terme de la séquence géométrique suivante.
\(\{2, 10, 50, 250, ...\}\)
Solution
Le premier terme est\(2\). Le ratio commun peut être trouvé en divisant le deuxième terme par le premier terme.
\(\dfrac{10}{2}=5\)
Le ratio commun est\(5\). Remplacez le ratio commun et le premier terme de la séquence dans la formule.
\[\begin{align*}a_n &= a_1r^{(n−1)} \\ a_n &= 2⋅5^{n−1} \end{align*}\]
Le graphique de cette séquence dans la figure\(\PageIndex{4}\) montre un schéma exponentiel.
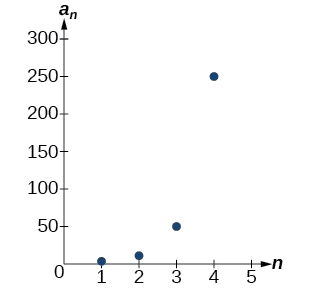
Figurine\(\PageIndex{4}\)
Écrivez une formule explicite pour la séquence géométrique suivante.
\(\{–1, 3, –9, 27, ...\}\)
- Réponse
-
\(a_n=−{(−3)}^{n−1}\)
Résolution de problèmes d'application avec des séquences géométriques
Dans les scénarios du monde réel impliquant des séquences arithmétiques, nous pouvons avoir besoin d'utiliser un terme initial de\(a_0\) au lieu de\(a_1\). Dans ces problèmes, nous pouvons modifier légèrement la formule explicite en utilisant la formule suivante :
\(a_n=a_0r^n\)
En 2013, le nombre d'élèves dans une petite école est de\(284\). On estime que la population étudiante augmentera\(4\%\) chaque année.
- Rédigez une formule pour la population étudiante.
- Estimez la population étudiante en 2020.
Solution
- La situation peut être modélisée par une séquence géométrique dont le terme initial est\(284\). La population étudiante sera celle\(104\%\) de l'année précédente, donc le ratio commun est\(1.04\).
\(P\)Soyons la population étudiante et\(n\) le nombre d'années après 2013. En utilisant la formule explicite pour une séquence géométrique, nous obtenons
\(P_n =284⋅{1.04}^n\)
- Nous pouvons trouver le nombre d'années écoulées depuis 2013 en soustrayant.
\(2020−2013=7\)
Nous cherchons la population après des\(7\) années. Nous pouvons nous\(7\) substituer\(n\) à l'estimation de la population en 2020.
\(P_7=284⋅{1.04}^7≈374\)
La population étudiante sera d'environ\(374\) 2020.
Une entreprise lance un nouveau site Web. Dans un premier temps, le nombre de visites est\(293\) dû à la curiosité. L'entreprise estime que le nombre de visites augmentera\(2.6%\) chaque semaine.
- Écrivez une formule pour le nombre de résultats.
- Estimez le nombre de visites en\(5\) semaines.
- Répondez à une
-
\(P_n = 293⋅1.026a^n\)
- Réponse b
-
Le nombre de visites sera d'environ\(333\).
Accédez à ces ressources en ligne pour obtenir des instructions et des exercices supplémentaires sur les séquences géométriques.
Équations clés
| formule récursive pour le nième terme d'une séquence géométrique | \(a_n=ra_{n−1}\),\(n≥2\) |
| formule explicite pour le nième terme d'une séquence géométrique | \(a_n=a_1r^{n−1}\) |
Key Concepts
- A geometric sequence is a sequence in which the ratio between any two consecutive terms is a constant.
- The constant ratio between two consecutive terms is called the common ratio.
- The common ratio can be found by dividing any term in the sequence by the previous term. See Example \(\PageIndex{1}\).
- The terms of a geometric sequence can be found by beginning with the first term and multiplying by the common ratio repeatedly. See Example \(\PageIndex{2}\) and Example \(\PageIndex{4}\).
- A recursive formula for a geometric sequence with common ratio \(r\) is given by \(a_n=ra_{n–1}\) for \(n≥2\).
- As with any recursive formula, the initial term of the sequence must be given. See Example \(\PageIndex{3}\).
- An explicit formula for a geometric sequence with common ratio \(r\) is given by \(a_n=a_1r^{n–1}\). See Example \(\PageIndex{5}\).
- In application problems, we sometimes alter the explicit formula slightly to \(a_n=a_0r^n\). See Example \(\PageIndex{6}\).


