13.1 : Les séquences et leurs notations

Last updated
Save as PDF

Page ID: 195009

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objectifs d'apprentissage

Écrivez les termes d'une séquence définie par une formule explicite.
Écrivez les termes d'une séquence définie par une formule récursive.
Utilisez la notation factorielle.

Une société de jeux vidéo lance une nouvelle campagne publicitaire passionnante. Ils prévoient que le nombre de visites en ligne sur leur site Web, ou de visites, doublera chaque jour. Le modèle qu'ils utilisent$2$ montre les touches le premier$4$ jour, le deuxième$8$ jour, le troisième jour, etc. (Tableau$\PageIndex{1}$).

Tableau$\PageIndex{1}$
Journée	1	2	3	4	5	...
Hits	2	4	8	16	32	...

Si leur modèle se poursuit, combien de visites y aura-t-il à la fin du mois ? Pour répondre à cette question, nous devons d'abord savoir comment déterminer une liste de nombres écrits dans un ordre précis. Dans cette section, nous allons explorer ces types de listes ordonnées.

Écrire les termes d'une séquence définie par une formule explicite

Une façon de décrire une liste ordonnée de nombres consiste à la présenter sous la forme d'une séquence. Une séquence est une fonction dont le domaine est un sous-ensemble des nombres de comptage. La séquence établie par le nombre de visites sur le site Web est

$\{ 2,4,8,16,32,…\}$

Les points de suspension (...) indiquent que la séquence se poursuit indéfiniment. Chaque numéro de la séquence est appelé terme. Les cinq premiers termes de cette séquence sont$2$$4$,$8$,$16$, et$32$.

La liste de tous les termes d'une séquence peut s'avérer fastidieuse. Par exemple, pour connaître le nombre de visites sur le site Web à la fin du mois, il faudrait énumérer autant de termes que de$31$ termes. Une façon plus efficace de déterminer un terme spécifique consiste à écrire une formule pour définir la séquence.

Un type de formule est une formule explicite, qui définit les termes d'une séquence en fonction de leur position dans la séquence. Les formules explicites sont utiles si nous voulons trouver un terme spécifique d'une séquence sans trouver tous les termes précédents. Nous pouvons utiliser la formule pour trouver le nième terme de la séquence, où nn est un nombre positif. Dans notre exemple, chaque nombre de la séquence est le double du nombre précédent, nous pouvons donc utiliser des puissances de 2 pour écrire une formule pour le nième terme.

$Séquence de {2, 4, 8, 16, 32,...} exprimée sous forme exponentielle (c'est-à-dire {2^1, 2^2, 2^3,..., 2^n,...}$

Le premier terme de la séquence est$2^1=2$, le deuxième terme est$2^2=4$, le troisième terme est$2^3=8$, et ainsi de suite. Le nième terme de la séquence peut être trouvé en élevant 2 à la nième puissance. Une formule explicite pour une séquence est nommée par une lettre minuscule$a$,$b$,$c$... avec l'indice$n$. La formule explicite de cette séquence est

$a_n=2^n$

Maintenant que nous avons une formule pour le nième terme de la séquence, nous pouvons répondre à la question posée au début de cette section. On nous a demandé de connaître le nombre de visites à la fin du mois, soit 31 jours. ^{Pour connaître le nombre de visites le dernier jour du mois, il faut trouver le 31e terme de la séquence.} Nous allons remplacer 31 par$n$ dans la formule.

\[ \begin{align*} a_{31}=2^{31} \\ [5pt] &=2,147,483,648 \end{align*}\]

Si la tendance au doublement se poursuit, l'entreprise sera touchée le dernier jour du mois.$2,147,483,648$ Cela représente plus d'un$2.1$ milliard de visites ! Ce chiffre énorme est probablement un peu irréaliste car il ne tient pas compte de l'intérêt des consommateurs et de la concurrence. Cela donne toutefois à l'entreprise un point de départ à partir duquel elle peut prendre des décisions commerciales.

Une autre façon de représenter la séquence consiste à utiliser un tableau. Les cinq premiers termes de la séquence et le nième terme de la séquence sont présentés dans le tableau$\PageIndex{2}$.

**Tableau$\PageIndex{2}$**
$n$	1	2	3	4	5	$n$
$n^{th}$durée de la séquence,$a_n$	2	4	8	16	32	$2^n$

La représentation graphique fournit une représentation visuelle de la séquence sous la forme d'un ensemble de points distincts. Nous pouvons voir sur le graphique de la figure$\PageIndex{1}$ que le nombre de visites augmente à un rythme exponentiel. Cette séquence particulière forme une fonction exponentielle.

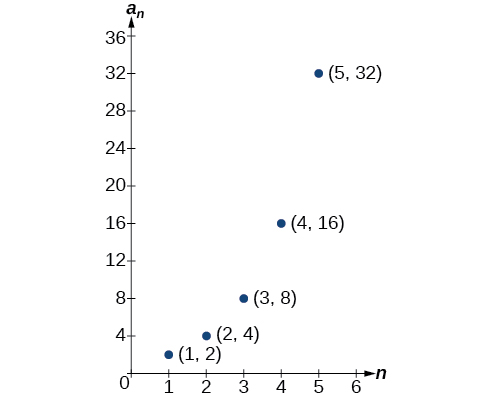
$Graphe d'une fonction exponentielle tracée, f (n) = 2^n, où l'axe x est étiqueté n et l'axe y est étiqueté a_n.$

Figurine$\PageIndex{1}$

Enfin, nous pouvons écrire cette séquence particulière sous la forme

$\{2,4,8,16,32,…,2^n,…\}$

Une séquence qui se poursuit indéfiniment est appelée séquence infinie. Le domaine d'une séquence infinie est l'ensemble des nombres de comptage. Si nous ne considérons que les premiers$10$ termes de la séquence, nous pourrions écrire

$\{2,4,8,16,32,…,2^n,…,1024\}$

Cette séquence est appelée séquence finie car elle ne se poursuit pas indéfiniment.

SÉQUENCE

Une séquence est une fonction dont le domaine est l'ensemble des entiers positifs. Une séquence finie est une séquence dont le domaine ne comprend que les premiers entiers$n$ positifs. Les nombres d'une séquence sont appelés termes. La variable$a$ avec un indice numérique est utilisée pour représenter les termes d'une séquence et pour indiquer la position du terme dans la séquence.

\[a_1,a_2,a_3,…,a_n,…\]

Nous appelons$a_1$ le premier terme de la séquence,$a_2$ le deuxième terme de$a_3$ la séquence, le troisième terme de la séquence, etc. Le terme$a_n$ est appelé nième terme de la séquence, ou terme général de la séquence. Une formule explicite définit le nième terme d'une séquence en utilisant la position du terme. Une séquence qui se poursuit indéfiniment est une séquence infinie.

Questions-réponses : Une séquence doit-elle toujours commencer par$a_1$?

Non. Dans certains problèmes, il peut être utile de définir le terme initial comme étant$a_0$ au lieu de$a_1$. Dans ces problèmes, le domaine de la fonction inclut$0$.

Comment : à partir d'une formule explicite, écrivez la première$n$ terms of a sequence

Remplacez chaque valeur de$n$ dans la formule. Commencez par$n=1$ trouver le premier terme,$a_1$.
Pour trouver le second terme$a_2$, utilisez$n=2$.
Continuez de la même manière jusqu'à ce que vous ayez identifié tous les termes nn.

Exemple$\PageIndex{1}$: Writing the Terms of a Sequence Defined by an Explicit Formula

Écrivez les cinq premiers termes de la séquence définie par la formule explicite$a_n=−3n+8$.

Solution

Substituer$n=1$ dans la formule. Répétez l'opération avec les valeurs$2$ jusqu'à$5$ pour$n$.

$\begin{array}{ll} n=1 & a_1=−3(1)+8=5 \\ n=2 & a_2=−3(2)+8=2 \\ n=3 & a_3=−3(3)+8=−1 \\ n=4 & a_4=−3(4)+8=−4 \\ n=5 & a_5=−3(5)+8=−7 \end{array}$

Les cinq premiers termes sont$\{5,2,−1,−4,−7\}$.

Analyse

Les valeurs de séquence peuvent être répertoriées dans un tableau. Un tableau, tel que Tableau$\PageIndex{3}$, est un moyen pratique de saisir la fonction dans un utilitaire de création graphique.

Tableau$\PageIndex{3}$
$n$	1	2	3	4	5
$a_n$	5	2	—1	—4	—7

Un graphique peut être créé à partir de ce tableau de valeurs. Sur le graphique de la figure$\PageIndex{2}$, nous pouvons voir que cette séquence représente une fonction linéaire, mais notez que le graphique n'est pas continu car le domaine se trouve uniquement sur les entiers positifs.

$Graphe d'un diagramme dispersé où l'axe x est étiqueté n et l'axe y est étiqueté a_n.$

Figurine$\PageIndex{2}$

Exercice$\PageIndex{1}$

Écrivez les cinq premiers termes de la séquence définie par la formule explicite$t_n=5n−4$.

Réponse: Les cinq premiers termes sont$\{1,6, 11, 16, 21\}$.

Étude de séquences alternées

Parfois, les séquences comportent des termes alternatifs. En fait, les termes peuvent en fait alterner en signe. Les étapes pour trouver les termes de la séquence sont les mêmes que si les signes n'alternaient pas. Toutefois, les termes qui en résulteront n'indiqueront pas d'augmentation ou de diminution en tant qu'$n$augmentations. Jetons un coup d'œil à la séquence suivante.

$\{2,−4,6,−8\}$

Notez que le premier terme est supérieur au deuxième terme, que le deuxième terme est inférieur au troisième terme et que le troisième terme est supérieur au quatrième terme. Cette tendance se poursuit à jamais. Ne réorganisez pas les termes par ordre numérique pour interpréter la séquence.

Comment : à partir d'une formule explicite avec des termes alternatifs, écrire les nn premiers termes d'une séquence

Remplacez chaque valeur de nn dans la formule. Commencez par$n=1$ trouver le premier terme,$a_1$. Le signe du terme est donné par le${(−1)}^n$ dans la formule explicite.
Pour trouver le second terme$a_2$, utilisez$n=2$.
Continuez de la même manière jusqu'à ce que vous ayez identifié tous les$n$ termes.

Exemple$\PageIndex{2}$: Writing the Terms of an Alternating Sequence Defined by an Explicit Formula

Écrivez les cinq premiers termes de la séquence.

$a_n=\dfrac{{(−1)}^nn^2}{n+1}$

Solution

$n=1$Substituez$n=2$, et ainsi de suite dans la formule.

$\begin{array}{ll} n=1 & a_1=\dfrac{{(−1)}^12^2}{1+1}=−\dfrac{1}{2} \\ n=2 & a_2=\dfrac{{(−1)}^22^2}{2+1}=\dfrac{4}{3} \\ n=3 & a_3=\dfrac{{(−1)}^33^2}{3+1}=−\dfrac{9}{4} \\ n=4 & a_4=\dfrac{{(−1)}^44^2}{4+1}=\dfrac{16}{5} \\ n=5 & a_5=\dfrac{{(−1)}^55^2}{5+1}=−\dfrac{25}{6} \end{array}$

Les cinq premiers termes sont$\{−12,43,−94,165,−256\}$.

Analyse

Le graphique de cette fonction, illustré dans la figure$\PageIndex{3}$, est différent de ceux que nous avons vus précédemment dans cette section car les termes de la séquence alternent entre des valeurs positives et négatives.

$Graphique d'un diagramme dispersé avec des points étiquetés : (1, -1/2), (2, 4/3), (3, -9/4), (4, 16/5) et (5, -25/6). L'axe X est étiqueté n et l'axe y est étiqueté a_n.$

Figurine$\PageIndex{3}$

Q&R : Dans l'exemple ci-dessus, est-ce que$(–1)$ to the power of $n$ account for the oscillations of signs?

Oui, la puissance peut être$n$,$n+1$$n−1$, et ainsi de suite, mais toute puissance impaire donnera un terme négatif, et toute puissance paire se traduira par un terme positif.

Exercice$\PageIndex{2}$

Écrivez les cinq premiers termes de la séquence :

$a_n=\dfrac{4n}{{(−2)}^n}$

Réponse: Les cinq premiers termes sont$\{−2, 2, −32, 1, −58\}$.

Étude de formules explicites par morceaux

Nous avons appris que les séquences sont des fonctions dont le domaine se situe au-dessus des entiers positifs. Cela est vrai pour d'autres types de fonctions, y compris certaines fonctions par morceaux. Rappelez-vous qu'une fonction par morceaux est une fonction définie par plusieurs sous-sections. Une formule différente peut représenter chaque sous-section individuelle.

Comment : à partir d'une formule explicite pour une fonction par morceaux, écrivez la première$n$ terms of a sequence

Identifiez la formule à laquelle$n=1$ s'applique.
Pour trouver le premier terme$a_1$, utilisez-le$n=1$ dans la formule appropriée.
Identifiez la formule à laquelle$n=2$ s'applique.
Pour trouver le second terme$a_2$, utilisez-le$n=2$ dans la formule appropriée.
Continuez de la même manière jusqu'à ce que vous ayez identifié tous les$n$ termes.

Exemple$\PageIndex{3}$: Writing the Terms of a Sequence Defined by a Piecewise Explicit Formula

Écrivez les six premiers termes de la séquence.

$a_n=\begin{cases}n^2\space \text{if n is not divisible by } 3\\\dfrac{n}{3} \text{if n is divisible by } 3\end{cases}$

Solution

Remplacez$n=1$$n=2$, et ainsi de suite dans la formule appropriée. $n^2$À utiliser lorsque$n$ ce n'est pas un multiple de$3$. À utiliser$n^3$ lorsque$n$ est un multiple de$3$.

$\begin{array}{ll} a_1=1^2=1 & 1 \text{ is not a multiple of }3. \text{ Use } n^2. \\ a_2=2^2=4 & 2 \text{ is not a multiple of }3 \text{ . Use }n^2. \\ a_3=\dfrac{3}{3}=1 & 3 \text{ is a multiple of }3 \text{. Use }\dfrac{n}{3}. \\ a_4=4^2=16 & 4 \text{ is not a multiple of }3. \text{ Use }n^2. \\ a_5=5^2=25 & 5 \text{ is not a multiple of } 3. \text{Use }n^2. \\ a_6=\dfrac{6}{3}=2 & 6 \text{ is a multiple of }3. \text{Use }\dfrac{n}{3} \end{array}$

Les six premiers termes sont$\{1, 4, 1, 16, 25, 2\}$.

Analyse

Un point sur trois du graphique illustré à la figure$\PageIndex{4}$ se distingue des deux points voisins. Cela se produit parce que la séquence a été définie par une fonction par morceaux.

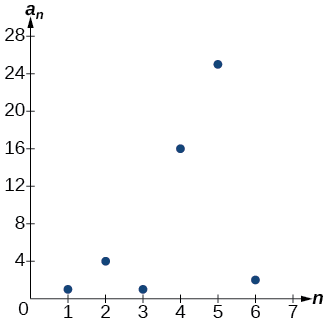
$Graphe d'un diagramme dispersé où l'axe x est étiqueté n et l'axe y est étiqueté a_n.$

Figurine$\PageIndex{4}$

Exercice$\PageIndex{3}$

Écrivez les six premiers termes de la séquence.

$a_n=\begin{cases}2n^3 \text{ if } n\text{ is odd} \\ \dfrac{5n}{2} \text{ if } n \text{ is even}\end{cases}$

Réponse: Les six premiers termes sont$\{2, 5, 54, 10, 250, 15\}$.

Trouver une formule explicite

Jusqu'à présent, on nous a donné la formule explicite et on nous a demandé de trouver un certain nombre de termes de la séquence. Parfois, la formule explicite pour le nième terme d'une séquence n'est pas donnée. Au lieu de cela, on nous donne plusieurs termes de la séquence. Lorsque cela se produit, nous pouvons travailler en sens inverse pour trouver une formule explicite à partir des premiers termes d'une séquence. La clé pour trouver une formule explicite est de rechercher un modèle dans les termes. Gardez à l'esprit que le modèle peut impliquer une alternance de termes, de formules pour les numérateurs, de formules pour les dénominateurs, d'exposants ou de bases.

Comment : à partir des premiers termes d'une séquence, trouver une formule explicite pour la séquence

Recherchez un modèle parmi les termes.
Si les termes sont des fractions, recherchez un modèle distinct entre les numérateurs et les dénominateurs.
Recherchez un schéma parmi les signes des termes.
Écrivez une formule pour$a_n$ en termes de$n$. Testez votre formule pour$n=1$$n=2$, et$n=3$.

Exemple$\PageIndex{4}$: Writing an Explicit Formula for the nth Term of a Sequence

Écrivez une formule explicite pour le nième terme de chaque séquence.

$\{−\dfrac{2}{11}, \dfrac{3}{13}, −\dfrac{4}{15}, \dfrac{5}{17}, −\dfrac{6}{19},…\}$
$\{−\dfrac{2}{25}, −\dfrac{2}{125}, −\dfrac{2}{625}, −\dfrac{2}{3,125}, −\dfrac{2}{15,625},…\}$
$\{e^4,e^5,e^6,e^7,e^8,…\}$

Solution

Recherchez le motif dans chaque séquence.

Les termes alternent entre positif et négatif. Nous pouvons${(−1)}^n$ les utiliser pour alterner les termes. Le numérateur peut être représenté par$n+1$. Le dénominateur peut être représenté par$2n+9$.
$a_n=\dfrac{{(−1)}^n(n+1)}{2n+9}$
Les termes sont tous négatifs.
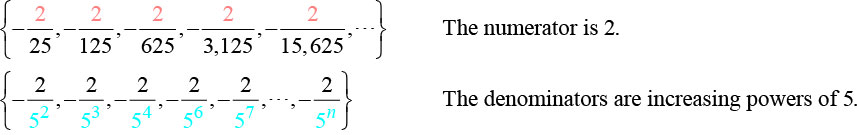
Nous savons donc que la fraction est négative, que le numérateur l'est$2$ et que le dénominateur peut être représenté par$5n+1$.

$a_n=−\dfrac{2}{5^{n+1}}$
Les termes sont des pouvoirs de$e$. $n=1$En effet, le premier terme est$e^4$ tel que l'exposant doit être$n+3$.
$a_n=e^{n+3}$

Exercice$\PageIndex{4A}$

Écrivez une formule explicite pour le nième terme de la séquence.

$\{9,−81,729,−6,561,59,049,…\}$

Réponse: $a_n={(−1)}^{n+1}9^n$

Exercice$\PageIndex{4B}$

Écrivez une formule explicite pour le nième terme de la séquence.

$\{−34,−98,−2712,−8116,−24320,...\}$

Réponse: $a_n=−\dfrac{3^n}{4n}$

Exercice$\PageIndex{4C}$

Écrivez une formule explicite pour le nième terme de la séquence.

$\left \{ \dfrac{1}{e^2}, \dfrac{1}{e}, 1, e, e^2,... \right \}$

Réponse: $a_n=e^{n−3}$

Écrire les termes d'une séquence définie par une formule récursive

Les séquences apparaissent naturellement dans les modèles de croissance des coquilles de nautilus, des pommes de pin, des branches d'arbres et de nombreuses autres structures naturelles. Nous pouvons voir la séquence dans la disposition des feuilles ou des branches, dans le nombre de pétales d'une fleur ou dans le motif des chambres d'une coquille de nautilus. Leur croissance suit la séquence de Fibonacci, une séquence célèbre dans laquelle chaque terme peut être trouvé en ajoutant les deux termes précédents. Les chiffres de la séquence sont$1, 1, 2, 3, 5, 8, 13, 21, 34,….$ D'autres exemples du monde naturel qui présentent la séquence de Fibonacci sont le lis Calla, qui n'a qu'un seul pétale, la Susan aux yeux noirs avec des$13$ pétales, et différentes variétés de marguerites pouvant avoir$21$ ou$34$ pétales.

Chaque terme de la séquence de Fibonacci dépend des termes qui le précèdent. La séquence de Fibonacci ne peut pas être facilement écrite à l'aide d'une formule explicite. Nous décrivons plutôt la séquence à l'aide d'une formule récursive, une formule qui définit les termes d'une séquence à l'aide de termes précédents.

Une formule récursive comporte toujours deux parties : la valeur d'un terme (ou de termes) initial et une équation définie$a_n$ en termes de termes précédents. Supposons par exemple que nous sachions ce qui suit :

\[\begin{align*} a_1 &= 3 \\ a_n &= 2a_{n−1}−1 , \text{ for }n≥2 \end{align*}\]

Nous pouvons trouver les termes suivants de la séquence en utilisant le premier terme.

\[\begin{align*} a_1 &= 3 \\ a_2 &= 2a_1−1=2(3)−1=5 \\ a_3 &= 2a_2−1=2(5)−1=9 \\ a_4 &= 2a_3−1=2(9)−1=17 \end{align*}\]

Les quatre premiers termes de la séquence sont donc$\{3, 5, 9, 17\}$.

La formule récursive de la séquence de Fibonacci énonce les deux premiers termes et définit chaque terme successif comme la somme des deux termes précédents.

\[\begin{align*}a_1 &= 1 \\ a_2 &= 1 \\ a_n &= a_{n−1}+a_{n−2} \text{, for }n≥3 \end{align*}\]

Pour trouver le dixième terme de la séquence, par exemple, il faudrait ajouter les huitième et neuvième termes. On nous a dit précédemment que les huitième et neuvième mandats sont$21$$34$ et donc

$a_{10}=a_9+a_8=34+21=55$

FORMULE RÉCURSIVE

Une formule récursive est une formule qui définit chaque terme d'une séquence à l'aide du ou des termes précédents. Les formules récursives doivent toujours indiquer le ou les termes initiaux de la séquence.

Q&R : Les deux premiers termes doivent-ils toujours être donnés dans une formule récursive ?

Non. La séquence de Fibonacci définit chaque terme en utilisant les deux termes précédents, mais de nombreuses formules récursives définissent chaque terme en utilisant un seul terme précédent. Ces séquences n'ont besoin que du premier terme pour être définies.

Comment : à partir d'une formule récursive avec uniquement le premier terme fourni, écrire les n premiers termes d'une séquence

Identifiez le terme initial$a_1$, qui est indiqué dans la formule. C'est le premier mandat.
Pour trouver le second terme$a_2$, remplacez le terme initial dans la formule par$a_{n−1}$. Résoudre.
Pour trouver le troisième terme$a_3$, remplacez le deuxième terme dans la formule. Résoudre.
Répétez l'opération jusqu'à ce que vous soyez résolu pour le nième mandat.

Exemple$\PageIndex{5}$: Writing the Terms of a Sequence Defined by a Recursive Formula

Écrivez les cinq premiers termes de la séquence définie par la formule récursive.

\[\begin{align*}a_1 &= 9 \\ a_n &= 3a_{n−1}−20 , \text{ for }n≥2 \end{align*}\]

Solution

Le premier terme est indiqué dans la formule. Pour chaque terme suivant, nous le$a_n−1$ remplaçons par la valeur du terme précédent.

$\begin{array}{ll} n=1 & a_1=9 \\ n=2 & a_2=3a_1−20=3(9)−20=27−20=7 \\ n=3 & a_3=3a_2−20=3(7)−20=21−20=1 \\ n=4 & a_4=3a_3−20=3(1)−20=3−20=−17 \\ n=5 & a_5=3a_4−20=3(−17)−20=−51−20=−71 \end{array}$

Les cinq premiers termes sont$\{9, 7, 1, –17, –71\}$. Voir la figure$\PageIndex{5}$.

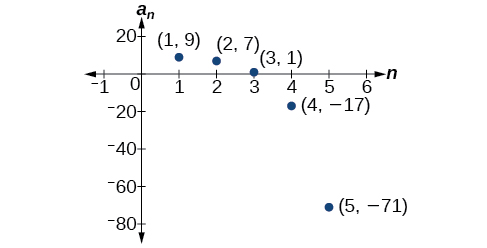
$Graphique d'un diagramme dispersé avec des points étiquetés : (1, 9), (2, 7), (3, 1), (4, -17) et (5, -71). L'axe X est étiqueté n et l'axe y est étiqueté a_n.$

Figurine$\PageIndex{5}$

Exercice$\PageIndex{5}$

Écrivez les cinq premiers termes de la séquence définie par la formule récursive.

\[\begin{align*} a_1 &= 2 \\ a_n &= 2a_{n−1}+1 , \text{ for }n≥2 \end{align*}\]

Réponse: $\{2, 5, 11, 23, 47\}$

Comment : à partir d'une formule récursive avec deux termes initiaux, écrire le premier$n$ terms of a sequence

Identifiez le terme initial$a_1$, qui est indiqué dans la formule.
Identifiez le second terme$a_2$, qui est indiqué dans la formule.
Pour trouver le troisième terme, remplacez le terme initial et le deuxième terme dans la formule. Évaluer.
Répétez l'opération jusqu'à ce que vous ayez évalué le nième terme.

Exemple$\PageIndex{6}$: Writing the Terms of a Sequence Defined by a Recursive Formula

Écrivez les six premiers termes de la séquence définie par la formule récursive.

\[\begin{align*} a_1 &=1 \\ a_2 &= 2 \\ a_n &= 3a_{n−1}+4a_{n−2} , \text{ for }n≥3 \end{align*}\]

Solution

Les deux premiers termes sont donnés. Pour chaque terme suivant, nous$a_{n−2}$ remplaçons$a_{n−1}$ et par les valeurs des deux termes précédents.

$\begin{array}{ll} n=3 & a_3=3a_2+4a_1=3(2)+4(1)=10 \\ n=4 & a_4=3a_3+4a_2=3(10)+4(2)=38 \\ n=5 & a_5=3a_4+4a_3=3(38)+4(10)=154 \\ n=6 & a_6=3a_5+4a_4=3(154)+4(38)=614 \end{array}$

Les six premiers termes sont$\{1,2,10,38,154,614\}$. Voir la figure$\PageIndex{6}$.

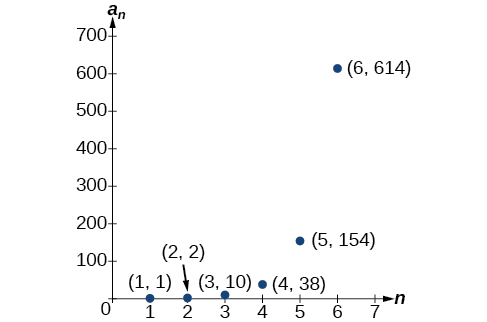
$Graphique d'un diagramme dispersé avec des points étiquetés : (1, 1), (2, 2), (3, 10), (4, 38), (5, 154) et (6, 614). L'axe X est étiqueté n et l'axe y est étiqueté a_n.$

Figurine$\PageIndex{6}$

Exercice$\PageIndex{6}$

Écrivez les premiers$8$ termes de la séquence définie par la formule récursive.

\[\begin{align*}a_1 &= 0 \\ a_2 &= 1 \\ a_3 &= 1 \\ a_n &= \dfrac{a_{n−1}}{a_{n−2}}+a_{n−3} , \text{ for }n≥4 \end{align*}\]

Réponse: $\left \{0, 1, 1, 1, 2, 3, 52, 176 \right \}$.

Utilisation de la notation factorielle

Les formules de certaines séquences incluent des produits d'entiers positifs consécutifs. $n$factoriel, écrit comme$n!$, est le produit des entiers positifs de$1$ à$n$. Par exemple,

\[\begin{align*}4! &= 4⋅3⋅2⋅1=24 \\ 5! &= 5⋅4⋅3⋅2⋅1=120 \end{align*}\]

Un exemple de formule contenant une factorielle est$a_n=(n+1)!$. Le sixième terme de la séquence peut être trouvé en remplaçant$6$ par$n$.

$a_6=(6+1)!=7!=7·6·5·4·3·2·1=5040$

La factorielle de tout nombre entier$n$ est$n(n−1)!$ Nous pouvons donc également la considérer$5!$ comme$5⋅4!$.

FACTORIEL

$n$factorielle est une opération mathématique qui peut être définie à l'aide d'une formule récursive. La factorielle de$n$, notée$n!$, est définie pour un entier positif$n$ comme suit :

\[\begin{align} 0! &= 1 \\ 1! &= 1 \\ n! &= n(n−1)(n−2)⋯(2)(1), \text{ for }n≥2 \end{align}\]

Le cas particulier$0!$ est défini comme$0!=1$.

Q&R : Est-il toujours possible de trouver des données factuelles à l'aide d'une calculatrice ?

Non. Les factorielles s'agrandissent très rapidement, même plus rapidement que les fonctions exponentielles ! Lorsque la sortie devient trop grande pour le calculateur, celui-ci ne sera pas en mesure de calculer la factorielle.

Exemple$\PageIndex{7}$: Writing the Terms of a Sequence Using Factorials

Écrivez les cinq premiers termes de la séquence définie par la formule explicite$a_n=\dfrac{5n}{(n+2)!}$.

Solution

$n=1$Substituez$n=2$, et ainsi de suite dans la formule.

$\begin{array}{ll} n=1 & a_1=\dfrac{5(1)}{(1+2)!}=\dfrac{5}{3!}=\dfrac{5}{3·2·1}=\dfrac{5}{6} \\ n=2 & a_2=\dfrac{5(2)}{(2+2)!}=\dfrac{10}{4!}=\dfrac{10}{4·3·2·1}=\dfrac{5}{12} \\ n=3 & a_3=\dfrac{5(3)}{(3+2)!}=\dfrac{15}{5!}=\dfrac{15}{5·4·3·2·1}=\dfrac{1}{8} \\ n=4 & a_4=\dfrac{5(4)}{(4+2)!}=\dfrac{20}{6!}=\dfrac{20}{6·5·4·3·2·1}=\dfrac{1}{36} \\ n=5 & a_5=\dfrac{5(5)}{(5+2)!}=\dfrac{25}{7!}=\dfrac{25}{7·6·5·4·3·2·1}=\dfrac{5}{1,008} \end{array}$

Les cinq premiers termes sont$\left \{\dfrac{5}{6}, \dfrac{5}{12}, \dfrac{1}{8}, \dfrac{1}{36}, \dfrac{5}{1,008} \right \}$.

Analyse

La figure$\PageIndex{7}$ montre le graphique de la séquence. Notez que, comme les factorielles croissent très rapidement, la présence du terme factoriel dans le dénominateur fait en sorte que le dénominateur devient beaucoup plus grand que le numérateur à mesure que nn augmente. Cela signifie que le quotient diminue et, comme le montre le diagramme des termes, que les termes diminuent et se rapprochent de zéro.

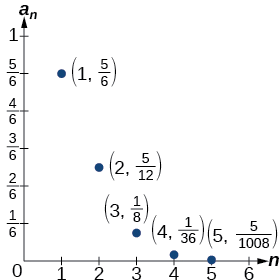
$13.2.7.PNGgraphe d'un diagramme dispersé avec des points étiquetés : (1, 5/6), (2, 5/12), (3, 1/8), (4, 1/36) et (5, 5/1008). L'axe X est étiqueté n et l'axe y est étiqueté a_n.$

Figurine$\PageIndex{7}$

Exercice$\PageIndex{7}$

Écrivez les cinq premiers termes de la séquence définie par la formule explicite$a_n=\dfrac{(n+1)!}{2n}$.

Réponse: Les cinq premiers termes sont$\left \{1, \dfrac{3}{2}, 4, 15, 72 \right \}$.

Médias

Accédez à cette ressource en ligne pour obtenir des instructions supplémentaires et vous entraîner avec les séquences.

Recherche de termes dans une séquence

Équations clés

Formule pour une factorielle

$0!=1$

$1!=1$

$n!=n(n−1)(n−2)⋯(2)(1)$, pour$n≥2$

Concepts clés

Une séquence est une liste de nombres, appelés termes, écrits dans un ordre précis.
Les formules explicites définissent chaque terme d'une séquence en utilisant la position du terme. Voir Exemple$\PageIndex{1}$$\PageIndex{2}$, Exemple et Exemple$\PageIndex{3}$.
Une formule explicite pour le dixième terme d'une séquence peut être écrite en analysant le schéma de plusieurs termes. Voir l'exemple$\PageIndex{4}$.
Les formules récursives définissent chaque terme d'une séquence à l'aide de termes précédents.
Les formules récursives doivent indiquer le ou les termes initiaux d'une séquence.
Un ensemble de termes peut être écrit à l'aide d'une formule récursive. Voir Exemple$\PageIndex{5}$ et Exemple$\PageIndex{6}$.
Une factorielle est une opération mathématique qui peut être définie de manière récursive.
La factorielle de$n$ est le produit de tous les nombres entiers compris entre$1$ et$n$. Voir l'exemple$\PageIndex{7}$.

Contributors and Attributions

Template:ContribOpenStaxPreCalc

\(n\)	1	2	3	4	5	\(n\)
\(n^{th}\)durée de la séquence,\(a_n\)	2	4	8	16	32	\(2^n\)

SÉQUENCE

Questions-réponses : Une séquence doit-elle toujours commencer par\(a_1\)?

Comment : à partir d'une formule explicite, écrivez la première\(n\) terms of a sequence

Exemple\(\PageIndex{1}\): Writing the Terms of a Sequence Defined by an Explicit Formula

Exercice\(\PageIndex{1}\)

Comment : à partir d'une formule explicite avec des termes alternatifs, écrire les nn premiers termes d'une séquence

Exemple\(\PageIndex{2}\): Writing the Terms of an Alternating Sequence Defined by an Explicit Formula

Exercice\(\PageIndex{2}\)

Comment : à partir d'une formule explicite pour une fonction par morceaux, écrivez la première\(n\) terms of a sequence

Exemple\(\PageIndex{3}\): Writing the Terms of a Sequence Defined by a Piecewise Explicit Formula

Exercice\(\PageIndex{3}\)

Comment : à partir des premiers termes d'une séquence, trouver une formule explicite pour la séquence

Exemple\(\PageIndex{4}\): Writing an Explicit Formula for the nth Term of a Sequence

Exercice\(\PageIndex{4A}\)

Exercice\(\PageIndex{4B}\)

Exercice\(\PageIndex{4C}\)

FORMULE RÉCURSIVE

Q&R : Les deux premiers termes doivent-ils toujours être donnés dans une formule récursive ?

Exemple\(\PageIndex{5}\): Writing the Terms of a Sequence Defined by a Recursive Formula

Exercice\(\PageIndex{5}\)

Exemple\(\PageIndex{6}\): Writing the Terms of a Sequence Defined by a Recursive Formula

Exercice\(\PageIndex{6}\)

FACTORIEL

Q&R : Est-il toujours possible de trouver des données factuelles à l'aide d'une calculatrice ?

Exemple\(\PageIndex{7}\): Writing the Terms of a Sequence Using Factorials

Exercice\(\PageIndex{7}\)

Objectifs d'apprentissage

Écrire les termes d'une séquence définie par une formule explicite

SÉQUENCE

Comment : à partir d'une formule explicite, écrivez la première\(n\) terms of a sequence

Exemple\(\PageIndex{1}\): Writing the Terms of a Sequence Defined by an Explicit Formula

Exercice\(\PageIndex{1}\)

Étude de séquences alternées

Comment : à partir d'une formule explicite avec des termes alternatifs, écrire les nn premiers termes d'une séquence

Exemple\(\PageIndex{2}\): Writing the Terms of an Alternating Sequence Defined by an Explicit Formula

Q&R : Dans l'exemple ci-dessus, est-ce que\((–1)\) to the power of \(n\) account for the oscillations of signs?

Exercice\(\PageIndex{2}\)

Étude de formules explicites par morceaux

Comment : à partir d'une formule explicite pour une fonction par morceaux, écrivez la première\(n\) terms of a sequence

Exemple\(\PageIndex{3}\): Writing the Terms of a Sequence Defined by a Piecewise Explicit Formula

Exercice\(\PageIndex{3}\)

Trouver une formule explicite

Comment : à partir des premiers termes d'une séquence, trouver une formule explicite pour la séquence

Exemple\(\PageIndex{4}\): Writing an Explicit Formula for the nth Term of a Sequence

Exercice\(\PageIndex{4A}\)

Exercice\(\PageIndex{4B}\)

Exercice\(\PageIndex{4C}\)

Écrire les termes d'une séquence définie par une formule récursive

Comment : à partir d'une formule récursive avec uniquement le premier terme fourni, écrire les n premiers termes d'une séquence

Exemple\(\PageIndex{5}\): Writing the Terms of a Sequence Defined by a Recursive Formula

Exercice\(\PageIndex{5}\)

Comment : à partir d'une formule récursive avec deux termes initiaux, écrire le premier\(n\) terms of a sequence

Exemple\(\PageIndex{6}\): Writing the Terms of a Sequence Defined by a Recursive Formula

Exercice\(\PageIndex{6}\)

Utilisation de la notation factorielle

FACTORIEL

Exemple\(\PageIndex{7}\): Writing the Terms of a Sequence Using Factorials

Exercice\(\PageIndex{7}\)

Médias

Équations clés

Concepts clés

Contributors and Attributions