12.5 : Sections coniques en coordonnées polaires
- Page ID
- 195630
- Identifiez une conique sous forme polaire.
- Représentez graphiquement les équations polaires des coniques.
- Définissez les coniques en termes de focus et de directrix.
La plupart d'entre nous connaissent les mouvements orbitaux, tels que le mouvement d'une planète autour du soleil ou d'un électron autour d'un noyau atomique. Au sein du système planétaire, les orbites des planètes, des astéroïdes et des comètes autour d'un corps céleste plus grand sont souvent elliptiques. Les comètes peuvent toutefois prendre une orbite parabolique ou hyperbolique à la place. Et, en réalité, les caractéristiques des orbites des planètes peuvent varier au fil du temps. Chaque orbite est liée à l'emplacement du corps céleste en orbite ainsi qu'à la distance et à la direction de la planète ou de tout autre objet par rapport à ce corps. Par conséquent, nous avons tendance à utiliser des coordonnées polaires pour représenter ces orbites.
Sur une orbite elliptique, le périapsis est le point auquel les deux objets sont les plus proches, et l'apoapsie est le point où ils sont le plus éloignés l'un de l'autre. En général, la vitesse du corps en orbite tend à augmenter à l'approche du périapsis et à diminuer à l'approche de l'apoapsis. Certains objets atteignent une vitesse d'échappement, ce qui se traduit par une orbite infinie. Ces corps présentent une orbite parabolique ou hyperbolique autour d'un corps ; le corps en orbite se libère de l'attraction gravitationnelle du corps céleste et s'envole dans l'espace. Chacune de ces orbites peut être modélisée par une section conique dans le système de coordonnées polaires.
Identification d'une conique sous forme polaire
Toute conique peut être déterminée par trois caractéristiques : un foyer unique, une ligne fixe appelée directrice et le rapport des distances entre chacune et un point du graphique. Considérez la parabole\(x=2+y^2\) illustrée sur la figure\(\PageIndex{2}\).
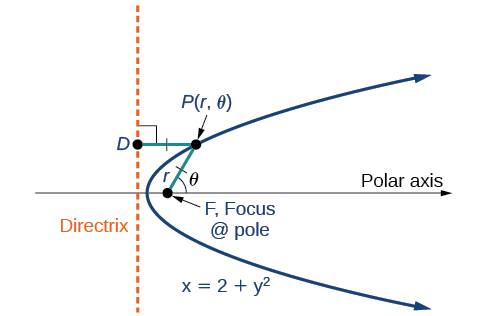
Nous avons déjà appris comment une parabole est définie par le foyer (un point fixe) et la directrice (une ligne fixe). Dans cette section, nous allons apprendre à définir n'importe quelle conique du système de coordonnées polaires en termes de point fixe, de foyer\(P(r,\theta)\) au pôle, et d'une ligne, la directrice, perpendiculaire à l'axe polaire.
S'il s'\(F\)agit d'un point fixe, du point focal, et\(D\) d'une ligne fixe, la directrice, alors nous pouvons laisser\(e\) un nombre positif fixe, appelé excentricité, que nous pouvons définir comme le rapport des distances entre un point du graphique et le point du graphique et le point du graphique directrice. Ensuite, l'ensemble de tous les points\(P\)\(e=\dfrac{PF}{PD}\) est une conique. En d'autres termes, nous pouvons définir une conique comme l'ensemble de tous les points\(P\) avec la propriété que le rapport entre la distance\(P\) de\(F\) et la distance de\(P\) et\(D\) est égal à la constante\(e\).
Pour une conique excentrique\(e\),
- si\(0≤e<1\), la conique est une ellipse
- si\(e=1\), la conique est une parabole
- si\(e>1\), la conique est une hyperbole
Avec cette définition, nous pouvons maintenant définir une conique en termes de directrice\(x=\pm p\), d'excentricité\(e\) et d'angle\(\theta\). Ainsi, chaque conique peut être écrite comme une équation polaire, une équation écrite en termes de\(r\) et\(\theta\).
Pour une conique dont le foyer est à l'origine, si la directrice est\(x=\pm p\), où\(p\) est un nombre réel positif, et que l'excentricité est un nombre réel positif\(e\), la conique possède une équation polaire
\[r=\dfrac{ep}{1\pm e \cos \theta}\]
Pour une conique dont le foyer est à l'origine, si la directrice est\(y=\pm p\), où\(p\) est un nombre réel positif, et que l'excentricité est un nombre réel positif\(e\), la conique possède une équation polaire
\[r=\dfrac{ep}{1\pm e \sin \theta}\]
- Multipliez le numérateur et le dénominateur par l'inverse de la constante du dénominateur pour réécrire l'équation sous forme standard.
- Identifiez l'excentricité\(e\) comme étant le coefficient de la fonction trigonométrique dans le dénominateur.
- Comparez\(e\) avec\(1\) pour déterminer la forme de la conique.
- Déterminez la directrice comme\(x=p\) si le cosinus était dans le dénominateur et\(y=p\) si le sinus était dans le dénominateur. \(ep\)Défini égal au numérateur sous forme standard pour résoudre\(x\) ou\(y\).
Pour chacune des équations suivantes, identifiez la conique avec le focus à l'origine, la directrice et l'excentricité.
- \(r=\dfrac{6}{3+2 \sin \theta}\)
- \(r=\dfrac{12}{4+5 \cos \theta}\)
- \(r=\dfrac{7}{2−2 \sin \theta}\)
Solution
Pour chacune des trois coniques, nous allons réécrire l'équation sous forme standard. La forme standard a\(1\) comme constante au dénominateur. Par conséquent, dans les trois parties, la première étape consistera à multiplier le numérateur et le dénominateur par l'inverse de la constante de l'équation d'origine\(\dfrac{1}{c}\), où\(c\) est cette constante.
- Multipliez le numérateur et le dénominateur par\(\dfrac{1}{3}\).
\(r=\dfrac{6}{3+2\sin \theta}⋅\dfrac{\left(\dfrac{1}{3}\right)}{\left(\dfrac{1}{3}\right)}=\dfrac{6\left(\dfrac{1}{3}\right)}{3\left(\dfrac{1}{3}\right)+2\left(\dfrac{1}{3}\right)\sin \theta}=\dfrac{2}{1+\dfrac{2}{3} \sin \theta}\)
Parce que\(\sin \theta\) c'est dans le dénominateur, la directrice est\(y=p\). Par rapport à la forme standard, notez que\(e=\dfrac{2}{3}\) .Par conséquent, à partir du numérateur,
\[\begin{align*} 2&=ep\\ 2&=\dfrac{2}{3}p\\ \left(\dfrac{3}{2}\right)2&=\left(\dfrac{3}{2}\right)\dfrac{2}{3}p\\ 3&=p \end{align*}\]
Puisque\(e<1\), la conique est une ellipse. L'excentricité existe\(e=\dfrac{2}{3}\) et la directrice l'est\(y=3\).
- Multipliez le numérateur et le dénominateur par\(\dfrac{1}{4}\).
\[\begin{align*} r&=\dfrac{12}{4+5 \cos \theta}\cdot \dfrac{\left(\dfrac{1}{4}\right)}{\left(\dfrac{1}{4}\right)}\\ r&=\dfrac{12\left(\dfrac{1}{4}\right)}{4\left(\dfrac{1}{4}\right)+5\left(\dfrac{1}{4}\right)\cos \theta}\\ r&=\dfrac{3}{1+\dfrac{5}{4} \cos \theta} \end{align*}\]
Parce que\(\cos \theta\) c'est dans le dénominateur, la directrice est\(x=p\). Par rapport à la forme standard,\(e=\dfrac{5}{4}\). Donc, à partir du numérateur,
\[\begin{align*} 3&=ep\\ 3&=\dfrac{5}{4}p\\ \left(\dfrac{4}{5}\right)3&=\left(\dfrac{4}{5}\right)\dfrac{5}{4}p\\ \dfrac{12}{5}&=p \end{align*}\]
Puisque\(e>1\), la conique est une hyperbole. L'excentricité existe\(e=\dfrac{5}{4}\) et la directrice l'est\(x=\dfrac{12}{5}=2.4\).
- Multipliez le numérateur et le dénominateur par\(\dfrac{1}{2}\).
\[\begin{align*} r&=\dfrac{7}{2-2 \sin \theta}\cdot \dfrac{\left(\dfrac{1}{2}\right)}{\left(\dfrac{1}{2}\right)}\\ r&=\dfrac{7\left(\dfrac{1}{2}\right)}{2\left(\dfrac{1}{2}\right)-2\left(\dfrac{1}{2}\right) \sin \theta}\\ r&=\dfrac{\dfrac{7}{2}}{1-\sin \theta} \end{align*}\]
Parce que le sinus est dans le dénominateur, la directrice l'est\(y=−p\). Par rapport à la forme standard,\(e=1\). Donc, à partir du numérateur,
\[\begin{align*} \dfrac{7}{2}&=ep\\ \dfrac{7}{2}&=(1)p\\ \dfrac{7}{2}&=p \end{align*}\]
Parce\(e=1\) que la conique est une parabole. L'excentricité existe\(e=1\) et la directrice l'est\(y=−\dfrac{7}{2}=−3.5\).
Identifiez la conique en mettant l'accent sur l'origine, la directrice et l'excentricité pour\(r=\dfrac{2}{3−\cos \theta}\).
- Réponse
-
ellipse\(e=\dfrac{1}{3}\) ;\(x=−2\)
Représentation graphique des équations polaires des coniques
Lorsque vous tracez un graphique en coordonnées cartésiennes, chaque section conique possède une équation unique. Ce n'est pas le cas lorsque vous tracez un graphique en coordonnées polaires. Nous devons utiliser l'excentricité d'une section conique pour déterminer le type de courbe à tracer, puis déterminer ses caractéristiques spécifiques. La première étape consiste à réécrire la conique sous forme standard comme nous l'avons fait dans l'exemple précédent. En d'autres termes, nous devons réécrire l'équation de telle sorte que le dénominateur commence par\(1\). Cela nous permet de déterminer\(e\) et donc la forme de la courbe. L'étape suivante consiste à substituer des valeurs à quelques points clés\(\theta\) et\(r\) à les résoudre pour tracer. La\(\theta\) valeur égale à\(0\)\(\dfrac{\pi}{2}\),\(\pi\), et\(\dfrac{3\pi}{2}\) fournit les sommets afin que nous puissions créer une esquisse approximative du graphe.
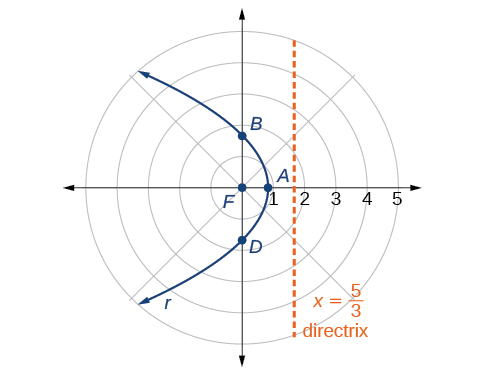
Graphe\(r=\dfrac{5}{3+3 \cos \theta}\).
Solution
Tout d'abord, nous réécrivons la conique sous forme standard en multipliant le numérateur et le dénominateur par l'inverse de\(3\), qui est\(\dfrac{1}{3}\).
\[\begin{align*} r &= \dfrac{5}{3+3 \cos \theta}=\dfrac{5\left(\dfrac{1}{3}\right)}{3\left(\dfrac{1}{3}\right)+3\left(\dfrac{1}{3}\right)\cos \theta} \\ r &= \dfrac{\dfrac{5}{3}}{1+\cos \theta} \end{align*}\]
Parce\(e=1\) que nous allons tracer une parabole avec un focus à l'origine. La fonction a un\(\cos \theta\), et il y a un signe d'addition dans le dénominateur, donc la directrice est\(x=p\).
\[\begin{align*} \dfrac{5}{3}&=ep\\ \dfrac{5}{3}&=(1)p\\ \dfrac{5}{3}&=p \end{align*}\]
La directrice est\(x=\dfrac{5}{3}\).
Tracer quelques points clés comme dans le tableau nous\(\PageIndex{1}\) permettra de voir les sommets. Voir la figure\(\PageIndex{3}\).
| UN | B | C | D | |
|---|---|---|---|---|
| \(\theta\) | \(0\) | \(\dfrac{\pi}{2}\) | \(\pi\) | \(\dfrac{3\pi}{2}\) |
| \(r=\dfrac{5}{3+3 \cos \theta}\) | \(\dfrac{5}{6}≈0.83\) | \(\dfrac{5}{3}≈1.67\) | indéfini | \(\dfrac{5}{3}≈1.67\) |
Nous pouvons vérifier notre résultat à l'aide d'un utilitaire graphique. Voir la figure\(\PageIndex{4}\).
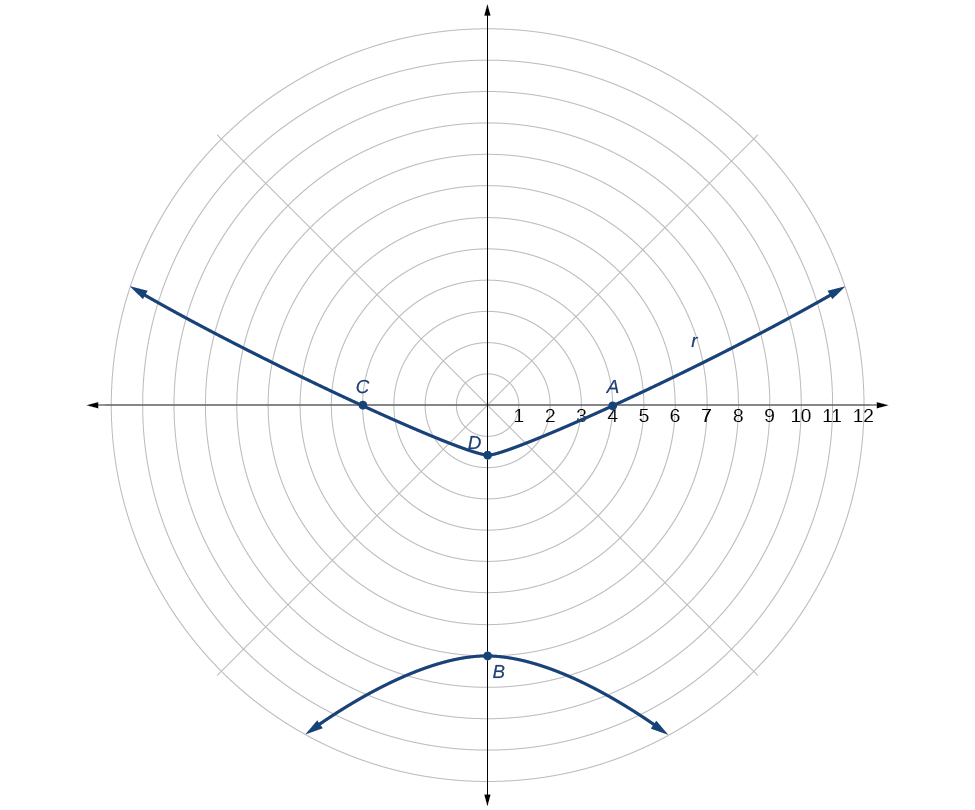
Graphe\(r=\dfrac{8}{2−3 \sin \theta}\).
Solution
Tout d'abord, nous réécrivons la conique sous forme standard en multipliant le numérateur et le dénominateur par l'inverse de\(2\), qui est\(\dfrac{1}{2}\).
\[\begin{align*} r &=\dfrac{8}{2−3\sin \theta}=\dfrac{8\left(\dfrac{1}{2}\right)}{2\left(\dfrac{1}{2}\right)−3\left(\dfrac{1}{2}\right)\sin \theta} \\ r &= \dfrac{4}{1−\dfrac{3}{2} \sin \theta} \end{align*}\]
Parce que\(e=\dfrac{3}{2}\) nous allons donc représenter graphiquement une hyperbole en mettant l'accent sur l'origine.\(e>1\) La fonction a un\(\sin \theta\) terme et il y a un signe de soustraction dans le dénominateur, donc la directrice l'est\(y=−p\).
\[\begin{align*} 4&=ep\\ 4&=\left(\dfrac{3}{2}\right)p\\ 4\left(\dfrac{2}{3}\right)&=p\\ \dfrac{8}{3}&=p \end{align*}\]
La directrice est\(y=−\dfrac{8}{3}\).
Tracer quelques points clés comme dans le tableau nous\(\PageIndex{2}\) permettra de voir les sommets. Voir la figure\(\PageIndex{5}\).
| UN | B | C | D | |
|---|---|---|---|---|
| \(\theta\) | \(0\) | \(\dfrac{\pi}{2}\) | \(\pi\) | \(\dfrac{3\pi}{2}\) |
| \(r=\dfrac{8}{2−3\sin \theta}\) | \(4\) | \(−8\) | \(4\) | \(\dfrac{8}{5}=1.6\) |
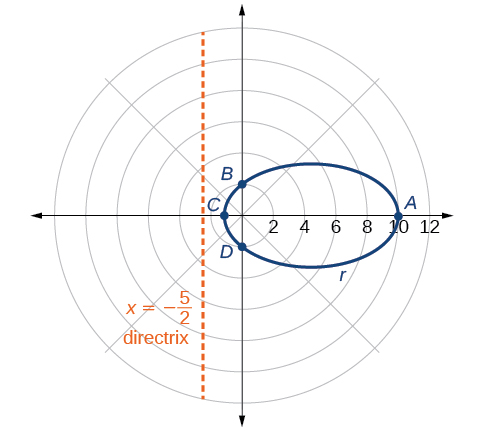
Graphe\(r=\dfrac{10}{5−4 \cos \theta}\).
Solution
Tout d'abord, nous réécrivons la conique sous forme standard en multipliant le numérateur et le dénominateur par l'inverse de 5, qui est\(\dfrac{1}{5}\).
\[\begin{align*} r &= \dfrac{10}{5−4\cos \theta}=\dfrac{10\left(\dfrac{1}{5}\right)}{5\left(\dfrac{1}{5}\right)−4\left(\dfrac{1}{5}\right)\cos \theta} \\ r &= \dfrac{2}{1−\dfrac{4}{5} \cos \theta} \end{align*}\]
Parce que\(e=\dfrac{4}{5}\)\(e<1\), donc, nous allons tracer une ellipse avec un focus à l'origine. La fonction a un\(\cos \theta\), et il y a un signe de soustraction dans le dénominateur, donc la directrice est\(x=−p\).
\[\begin{align*} 2&=ep\\ 2&=\left(\dfrac{4}{5}\right)p\\ 2\left(\dfrac{5}{4}\right)&=p\\ \dfrac{5}{2}&=p \end{align*}\]
La directrice est\(x=−\dfrac{5}{2}\).
Tracer quelques points clés comme dans le tableau nous\(\PageIndex{3}\) permettra de voir les sommets. Voir la figure\(\PageIndex{6}\).
| UN | B | C | D | |
|---|---|---|---|---|
| \(\theta\) | \(0\) | \(\dfrac{\pi}{2}\) | \(\pi\) | \(\dfrac{3\pi}{2}\) |
| \(r=\dfrac{10}{5−4 \cos \theta}\) | \(10\) | \(2\) | \(\dfrac{10}{9}≈1.1\) | \(2\) |
Analyse
Nous pouvons vérifier notre résultat à l'aide d'un utilitaire graphique. Voir la figure\(\PageIndex{7}\).
Graphe\(r=\dfrac{2}{4−\cos \theta}\).
- Réponse
-
Figurine\(\PageIndex{7}\)
Définition de Conics en termes de focus et de Directrix
Jusqu'à présent, nous avons utilisé des équations polaires de coniques pour décrire et représenter graphiquement la courbe. Nous allons maintenant travailler en sens inverse ; nous allons utiliser des informations sur l'origine, l'excentricité et la directrice pour déterminer l'équation polaire.
- Déterminez si la directrice est horizontale ou verticale. Si la directrice est donnée en termes de\(y\), nous utilisons la forme polaire générale en termes de sinus. Si la directrice est donnée en termes de\(x\), nous utilisons la forme polaire générale en termes de cosinus.
- Déterminez le signe du dénominateur. Si\(p<0\), utilisez la soustraction. Si\(p>0\), utilisez l'addition.
- Écrivez le coefficient de la fonction trigonométrique comme l'excentricité donnée.
- Écrivez la valeur absolue de\(p\) dans le numérateur et simplifiez l'équation.
Trouvez la forme polaire de la conique en mettant l'accent sur l'origine\(e=3\) et la directrice\(y=−2\).
Solution
La directrice est\(y=−p\), donc nous savons que la fonction trigonométrique du dénominateur est sinusoïdale.
Parce que\(y=−2\)\(–2<0\), donc, nous savons qu'il y a un signe de soustraction dans le dénominateur. Nous utilisons le formulaire standard de
\(r=\dfrac{ep}{1−e \sin \theta}\)
\(e=3\)et\(|−2|=2=p\).
Par conséquent,
\[\begin{align*} r&=\dfrac{(3)(2)}{1-3 \sin \theta}\\ r&=\dfrac{6}{1-3 \sin \theta} \end{align*}\]
Trouvez la forme polaire d'une conique en mettant l'accent sur l'origine\(e=\dfrac{3}{5}\), et la directrice\(x=4\).
Solution
Comme la directrice l'est\(x=p\), nous savons que la fonction du dénominateur est le cosinus. Parce que\(x=4\)\(4>0\), donc, nous savons qu'il y a un signe d'addition dans le dénominateur. Nous utilisons le formulaire standard de
\(r=\dfrac{ep}{1+e \cos \theta}\)
\(e=\dfrac{3}{5}\)et\(|4|=4=p\).
Par conséquent,
\[\begin{align*} r &= \dfrac{\left(\dfrac{3}{5}\right)(4)}{1+\dfrac{3}{5}\cos\theta} \\ r &= \dfrac{\dfrac{12}{5}}{1+\dfrac{3}{5}\cos\theta} \\ r &=\dfrac{\dfrac{12}{5}}{1\left(\dfrac{5}{5}\right)+\dfrac{3}{5}\cos\theta} \\ r &=\dfrac{\dfrac{12}{5}}{\dfrac{5}{5}+\dfrac{3}{5}\cos\theta} \\ r &= \dfrac{12}{5}⋅\dfrac{5}{5+3\cos\theta} \\ r &=\dfrac{12}{5+3\cos\theta} \end{align*}\]
Trouvez la forme polaire de la conique en mettant l'accent sur l'origine et la directrice\(x=−1\).\(e=1\)
- Réponse
-
\(r=\dfrac{1}{1−\cos\theta}\)
Convertissez la forme conique\(r=\dfrac{1}{5−5\sin \theta}\) en forme rectangulaire.
Solution
Nous allons réorganiser la formule pour utiliser les identités\(r=\sqrt{x^2+y^2}\)\(x=r \cos \theta\), et\(y=r \sin \theta\).
\[\begin{align*} r&=\dfrac{1}{5-5 \sin \theta} \\ r\cdot (5-5 \sin \theta)&=\dfrac{1}{5-5 \sin \theta}\cdot (5-5 \sin \theta)\qquad \text{Eliminate the fraction.} \\ 5r-5r \sin \theta&=1 \qquad \text{Distribute.} \\ 5r&=1+5r \sin \theta \qquad \text{Isolate }5r. \\ 25r^2&={(1+5r \sin \theta)}^2 \qquad \text{Square both sides. } \\ 25(x^2+y^2)&={(1+5y)}^2 \qquad \text{Substitute } r=\sqrt{x^2+y^2} \text{ and }y=r \sin \theta. \\ 25x^2+25y^2&=1+10y+25y^2 \qquad \text{Distribute and use FOIL. } \\ 25x^2-10y&=1 \qquad \text{Rearrange terms and set equal to 1.} \end{align*}\]
Convertissez la forme conique\(r=\dfrac{2}{1+2 \cos \theta}\) en forme rectangulaire.
- Réponse
-
\(4−8x+3x^2−y^2=0\)
Accédez à ces ressources en ligne pour obtenir des instructions supplémentaires et vous entraîner à utiliser les coniques en coordonnées polaires.
- Équations polaires des sections coniques
- Représentation graphique des équations polaires des coniques - 1
- Représentation graphique des équations polaires des coniques - 2
Visitez ce site Web pour des questions pratiques supplémentaires sur Learningpod.
Concepts clés
- Toute conique peut être déterminée par un seul foyer, l'excentricité correspondante et la directrice. Nous pouvons également définir une conique en termes de point fixe, le foyer\(P(r,\theta)\) au pôle, et d'une ligne, la directrice, qui est perpendiculaire à l'axe polaire.
- Une conique est l'ensemble de tous les points\(e=\dfrac{PF}{PD}\), où l'excentricité\(e\) est un nombre réel positif. Chaque conique peut être écrite en fonction de son équation polaire. Voir l'exemple\(\PageIndex{1}\).
- Les équations polaires des coniques peuvent être représentées graphiquement. Voir Exemple\(\PageIndex{2}\)\(\PageIndex{3}\), Exemple et Exemple\(\PageIndex{4}\).
- Les coniques peuvent être définies en termes de focalisation, de directrice et d'excentricité. Voir Exemple\(\PageIndex{5}\) et Exemple\(\PageIndex{6}\).
- Nous pouvons utiliser les identités\(r=\sqrt{x^2+y^2}\) et\(y=r \sin \theta\) convertir l'équation d'une forme conique d'une forme polaire à une forme rectangulaire.\(x=r \cos \theta\) Voir l'exemple\(\PageIndex{7}\).


