10.8 : Vecteurs
- Page ID
- 195546
- Visualisez les vecteurs de manière géométrique.
- Trouvez l'amplitude et la direction.
- Effectuez l'addition de vecteurs et la multiplication scalaire.
- Trouvez la forme du composant d'un vecteur.
- Trouvez le vecteur unitaire dans la direction de\(v\).
- Effectuez des opérations avec des vecteurs en termes de\(i\) et\(j\).
- Détermine le produit scalaire de deux vecteurs.
Un avion vole à une vitesse anémométrique de\(200\) miles par heure en direction d'un cap SE de\(140°\). Un vent du nord (du nord au sud) souffle à des\(16.2\) milles à l'heure, comme le montre la figure\(\PageIndex{1}\). Quelles sont la vitesse au sol et l'orientation réelle de l'avion ?
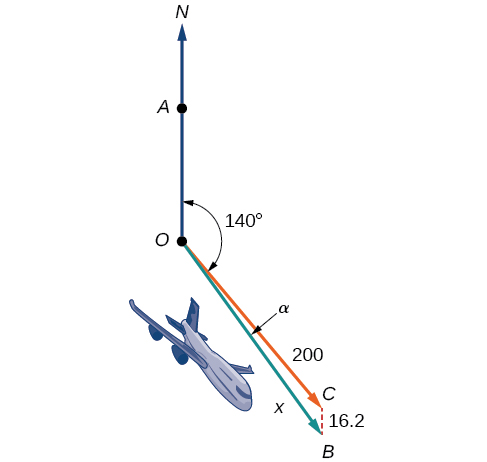
Figurine\(\PageIndex{1}\)
La vitesse du sol fait référence à la vitesse d'un avion par rapport au sol. La vitesse anémométrique fait référence à la vitesse qu'un avion peut parcourir par rapport à la masse d'air environnante. Ces deux quantités ne sont pas identiques en raison de l'effet du vent. Dans une section précédente, nous avons utilisé des triangles pour résoudre un problème similaire concernant le mouvement des bateaux. Plus loin dans cette section, nous examinerons la vitesse au sol et l'orientation de l'avion, tout en étudiant une autre approche des problèmes de ce type. Cependant, examinons d'abord les bases des vecteurs.
Une vue géométrique des vecteurs
Un vecteur est une quantité spécifique dessinée sous la forme d'un segment de ligne avec une pointe de flèche à une extrémité. Il a un point initial, où il commence, et un point terminal, où il se termine. Un vecteur est défini par sa magnitude, ou la longueur de la ligne, et sa direction, indiquée par une pointe de flèche au point terminal. Ainsi, un vecteur est un segment de ligne dirigé. Différents symboles permettent de distinguer les vecteurs des autres quantités :
- En minuscules, en gras, avec ou sans flèche en haut, telle que \(u\)\(w\),\(\overrightarrow{v}\),\(\overrightarrow{u}\),\(\overrightarrow{w}\).
- Étant donné le point initial\(P\) et le point terminal\(Q\), un vecteur peut être représenté sous la forme\(\overrightarrow{PQ}\). La pointe de flèche en haut indique qu'il ne s'agit pas simplement d'une ligne, mais d'un segment de ligne dirigé.
- Étant donné un point initial\((0,0)\) et un point terminal\((a,b)\), un vecteur peut être représenté par\(⟨a,b⟩\).
Ce dernier symbole\(⟨a,b⟩\) a une signification particulière. C'est ce qu'on appelle la position standard. Le vecteur de position possède un point initial\((0,0)\) et un point terminal\(⟨a,b⟩\). Pour transformer un vecteur en vecteur de position, nous pensons à la modification des coordonnées x et à la modification des coordonnées y. Ainsi, si le point initial d'un vecteur\(\overrightarrow{CD}\) est\(C(x_1,y_1)\) et que le point terminal est\(D(x_2,y_2)\), alors le vecteur de position est trouvé en calculant
\[\begin{align*} \overrightarrow{AB} &= ⟨x_2−x_1,y_2−y_1⟩ \\[4pt] &= ⟨a,b⟩ \end{align*}\]
Dans la figure\(\PageIndex{2}\), nous voyons le vecteur d'origine\(\overrightarrow{CD}\) et le vecteur de position\(\overrightarrow{AB}\).
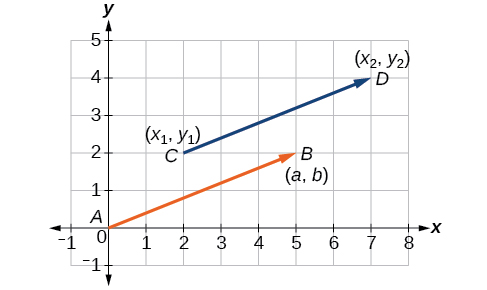
Figurine\(\PageIndex{2}\)
Un vecteur est un segment de ligne dirigé comportant un point initial et un point terminal. Les vecteurs sont identifiés par l'amplitude, ou la longueur de la ligne, et par la direction, représentée par la pointe de flèche pointant vers le point terminal. Le vecteur de position a un point initial à\((0,0)\) et est identifié par son point terminal\(⟨a,b⟩\).
Considérez le vecteur dont le point initial est\(P(2,3)\) et le point terminal est\(Q(6,4)\). Trouvez le vecteur de position.
Solution
Le vecteur de position est trouvé en soustrayant une\(x\) coordonnée de l'autre\(x\) coordonnée et une\(y\) coordonnée de l'autre\(y\) coordonnée. Ainsi
\[\begin{align*} v &= ⟨6−2,4−3⟩ \\[4pt] &=⟨4,1⟩ \end{align*}\]
Le vecteur de position commence à\((0,0)\) et se termine à\((4,1)\). Les graphes des deux vecteurs sont présentés sur la figure\(\PageIndex{3}\).
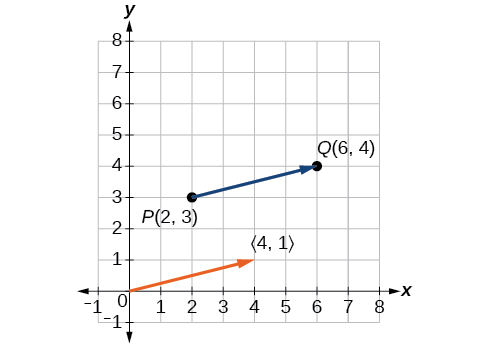
Figurine\(\PageIndex{3}\)
Nous voyons que le vecteur de position est\(⟨4,1⟩\).
Trouvez le vecteur de position étant donné que ce vecteur\(v\) a un point initial\((−3,2)\) et un point terminal à\((4,5)\), puis tracez les deux vecteurs dans le même plan.
Solution
Le vecteur de position est trouvé à l'aide du calcul suivant :
\[\begin{align*} v &= ⟨4−(−3),5−2⟩ \\[4pt] &= ⟨7,3⟩ \end{align*}\]
Ainsi, le vecteur de position commence à\((0,0)\) et se termine à\((7,3)\). Voir la figure\(\PageIndex{4}\).
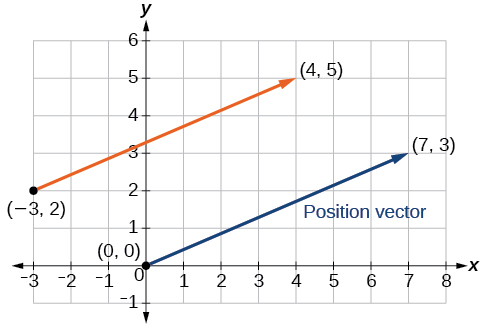
Figurine\(\PageIndex{4}\)
Tracez un vecteur\(\vec{v}\) reliant l'origine au point\((3,5)\).
- Réponse
-
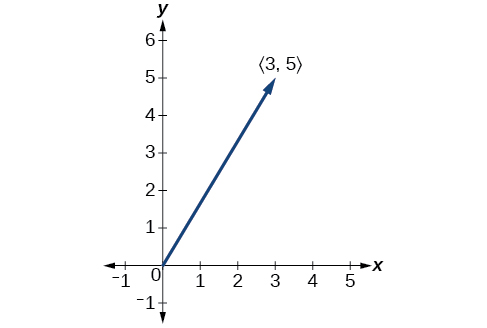
Figurine\(\PageIndex{5}\)
Déterminer l'ampleur et la direction
Pour travailler avec un vecteur, il faut pouvoir déterminer sa magnitude et sa direction. Nous trouvons sa magnitude à l'aide du théorème de Pythagore ou de la formule de distance, et nous trouvons sa direction à l'aide de la fonction de tangente inverse.
À partir d'un vecteur de position\(\vec{v}=⟨a,b⟩\), l'amplitude est déterminée par\(| v |=\sqrt{a^2+b^2}\). La direction est égale à l'angle formé avec l'\(x\)axe ou avec\(y\) l'axe, selon l'application. Pour un vecteur de position, la direction est déterminée par\(\tan \theta=\left(\dfrac{b}{a}\right)⇒\theta={\tan}^{−1}\left(\dfrac{b}{a}\right)\), comme illustré sur la figure\(\PageIndex{6}\).
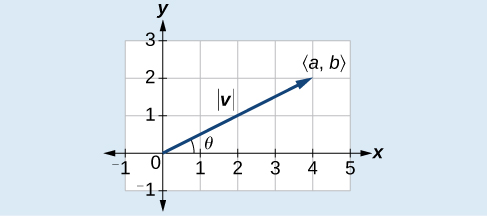
Figurine\(\PageIndex{6}\)
Deux vecteurs\(\vec{v}\) et\(\vec{u}\) sont considérés comme égaux s'ils ont la même amplitude et la même direction. De plus, si les deux vecteurs ont le même vecteur de position, ils sont égaux.
Trouvez l'amplitude et la direction du vecteur avec le point initial\(P(−8,1)\) et le point terminal\(Q(−2,−5)\). Dessinez le vecteur.
Solution
Commencez par trouver le vecteur de position.
\[\begin{align*} u &= ⟨−2,−(−8),−5−1⟩ \\[4pt] &= ⟨6,−6⟩ \end{align*}\]
Nous utilisons le théorème de Pythagore pour déterminer la magnitude.
\[\begin{align*} |u| &= \sqrt{{(6)}^2+{(−6)}^2} \\[4pt] &= \sqrt{72} \\[4pt] &=\sqrt{62} \end{align*}\]
La direction est donnée sous la forme
\[\begin{align*} \tan \theta & =\dfrac{−6}{6}=−1\rightarrow \theta={\tan}^{−1}(−1) \\[4pt] &= −45° \end{align*}\]
Cependant, l'angle se termine dans le quatrième quadrant, nous l'ajoutons\(360°\) pour obtenir un angle positif. Ainsi,\(−45°+360°=315°\). Voir la figure\(\PageIndex{7}\).
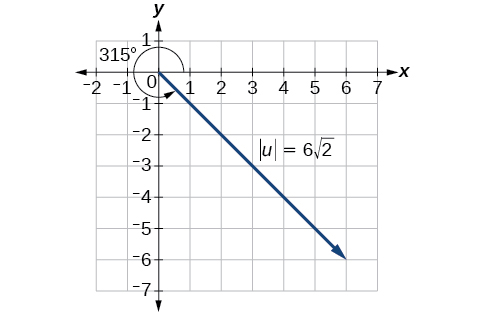
Figurine\(\PageIndex{7}\)
Montrez que le vecteur\(\vec{v}\) avec le point initial\((5,−3)\) et le point terminal à\((−1,2)\) est égal au vecteur\(\vec{u}\) avec le point initial à\((−1,−3)\) et le point terminal à\((−7,2)\). Tracez le vecteur de position sur la même grille que\(\vec{v}\) et\(\vec{u}\). Ensuite, déterminez l'amplitude et la direction de chaque vecteur.
Solution
Comme le montre la figure\(\PageIndex{8}\), dessinez le vecteur en\(\vec{v}\) commençant par le point initial\((5,−3)\) et le point terminal\((−1,2)\). Tracez le vecteur\(\vec{u}\) avec le point initial\((−1,−3)\) et le point terminal\((−7,2)\). Trouvez la position standard pour chacune d'elles.
Ensuite, recherchez et esquissez le vecteur de position pour\(\vec{v}\) et\(\vec{u}\). Nous avons
\[\begin{align*} v &= ⟨−1−5,2−(−3)⟩ \\[4pt] &= ⟨−6,5⟩u \\[4pt] &= ⟨−7−(−1),2−(−3)⟩ \\[4pt] & =⟨−6,5⟩ \end{align*}\]
Puisque les vecteurs de position sont les mêmes\(\vec{v}\) et\(\vec{u}\) sont identiques.
Une autre façon de vérifier l'égalité des vecteurs consiste à montrer que l'amplitude et la direction sont identiques pour les deux vecteurs. Pour montrer que les magnitudes sont égales, utilisez le théorème de Pythagore.
\[\begin{align*} |v| &= \sqrt{{(−1−5)}^2+{(2−(−3))}^2} \\[4pt] &= \sqrt{{(−6)}^2+{(5)}^2} \\[4pt] &= \sqrt{36+25} \\[4pt] &= \sqrt{61} \\[4pt] |u| &= \sqrt{{(−7−(−1))}^2+{(2−(−3))}^2} \\[4pt] &=\sqrt{{(−6)}^2+{(5)}^2} \\[4pt] &= \sqrt{36+25} \\[4pt] &= \sqrt{61} \end{align*}\]
Les magnitudes étant égales, nous devons maintenant vérifier la direction. L'utilisation de la fonction tangente avec le vecteur de position donne
\[\begin{align*} \tan \theta &= −\dfrac{5}{6}⇒\theta={\tan}^{−1}\left(−\dfrac{5}{6}\right) \\[4pt] & = −39.8° \end{align*}\]
Cependant, nous pouvons voir que le vecteur de position se termine dans le deuxième quadrant, donc nous ajoutons\(180°\). Ainsi, la direction est\(−39.8°+180°=140.2°\).
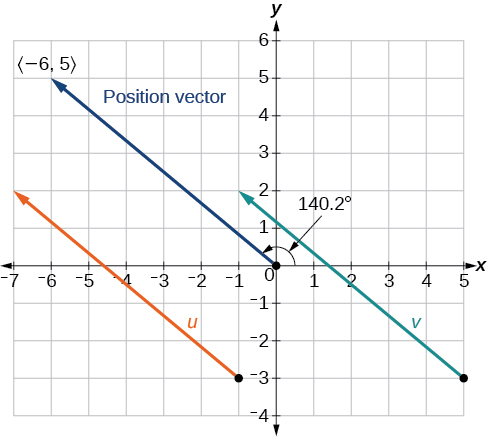
Figurine\(\PageIndex{8}\)
Effectuer une addition de vecteurs et une multiplication scalaire
Maintenant que nous comprenons les propriétés des vecteurs, nous pouvons effectuer des opérations les impliquant. Bien qu'il soit pratique de considérer le vecteur\(u=⟨x,y⟩\) comme une flèche ou un segment de ligne dirigée depuis l'origine jusqu'au point\((x,y)\), les vecteurs peuvent être situés n'importe où dans le plan. La somme de deux vecteurs\(\vec{u}\) et\(\vec{v}\), ou l'addition de vecteurs, produit un troisième vecteur\(\overrightarrow{u+ v}\), le vecteur résultant.
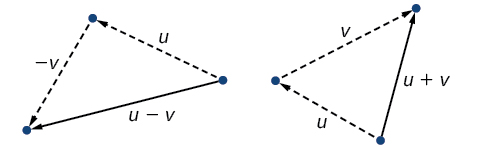
Pour le trouver\(\overrightarrow{u + v}\), nous dessinons d'abord le vecteur\(\vec{u}\), puis à partir de l'extrémité terminale de\(\vec{u}\), nous avons dessiné le vecteur\(\vec{v}\). En d'autres termes, nous avons le point initial de\(\vec{v}\) rencontre de l'extrémité terminale de\(\vec{u}\). Cette position correspond à l'idée que l'on se déplace le long du premier vecteur puis, à partir de son point terminal, on se déplace le long du second vecteur. La somme\(\overrightarrow{u + v}\) est le vecteur résultant car elle résulte de l'addition ou de la soustraction de deux vecteurs. Le vecteur résultant se déplace directement du début\(\vec{u}\) à la fin selon une trajectoire rectiligne, comme le montre la figure\(\PageIndex{9}\).\(\vec{v}\)
Figurine\(\PageIndex{9}\)
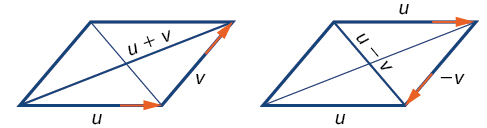
La soustraction vectorielle est similaire à l'addition de vecteurs. Pour le trouver\(\overrightarrow{u − v}\), visualisez-le sous forme de\(\overrightarrow{u + (−v)}\). Ajouter\(\overrightarrow{−v}\) consiste à inverser le sens de\(\vec{v}\) et à l'ajouter à la fin de\(\vec{u}\). Le nouveau vecteur commence au début\(\vec{u}\) et s'arrête au point final de\(\overrightarrow{−v}\). Voir la figure\(\PageIndex{10}\) pour un visuel qui compare l'addition et la soustraction de vecteurs à l'aide de parallélogrammes.
Figurine\(\PageIndex{10}\)
Étant donné\(u=⟨3,−2⟩\) et\(v=⟨−1,4⟩\), trouvez deux nouveaux vecteurs\(\overrightarrow{u + v}\), et\(\overrightarrow{u − v}\).
Solution
Pour trouver la somme de deux vecteurs, nous ajoutons les composantes. Ainsi,
\[ \begin{align*} u+v &= ⟨3,−2⟩+⟨−1,4⟩ \\[4pt] &= ⟨3+(−1),−2+4⟩ \\[4pt] &=⟨2,2⟩ \end{align*}\]
Voir la figure\(\PageIndex{11a}\).
Pour déterminer la différence entre deux vecteurs, ajoutez les composantes négatives de\(\vec{v}\) to\(\vec{u}\). Ainsi,
\[\begin{align*}u+(−v) &=⟨3,−2⟩+⟨1,−4⟩ \\[4pt] &= ⟨3+1,−2+(−4)⟩ \\[4pt] &= ⟨4,−6⟩ \end{align*}\]
Voir la figure\(\PageIndex{11b}\).
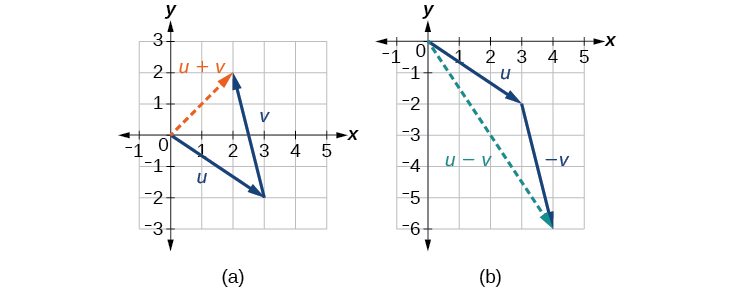
Figure\(\PageIndex{11}\) : (a) Somme de deux vecteurs (b) Différence de deux vecteurs
Multiplier par un scalaire
Alors que l'ajout et la soustraction de vecteurs nous donnent un nouveau vecteur avec une amplitude et une direction différentes, le processus de multiplication d'un vecteur par un scalaire, une constante, ne modifie que l'amplitude du vecteur ou la longueur de la ligne. La multiplication scalaire n'a aucun effet sur la direction sauf si le scalaire est négatif, auquel cas la direction du vecteur obtenu est opposée à la direction du vecteur d'origine.
La multiplication scalaire implique le produit d'un vecteur et d'un scalaire. Chaque composante du vecteur est multipliée par le scalaire. Ainsi, pour multiplier\(v=⟨a,b⟩\) par\(k\), nous avons
\(kv=⟨ka,kb⟩\)
Seule l'amplitude change, sauf si elle\(k\) est négative, puis le vecteur inverse la direction.
Vecteur donné \(\vec{v}=⟨3,1⟩\)\(3\vec{v}\)\(\dfrac{1}{2}\), trouver et\(\vec{−v}\).
Solution
Voir la figure\(\PageIndex{12}\) pour une interprétation géométrique. Si\(\vec{v}=⟨3,1⟩\), alors
\[\begin{align*} 3v &= ⟨3⋅3,3⋅1⟩ \\[4pt] &= ⟨9,3⟩ \\[4pt] \dfrac{1}{2}v &= ⟨\dfrac{1}{2}⋅3,\dfrac{1}{2}⋅1⟩ \\[4pt] &=⟨\dfrac{3}{2},\dfrac{1}{2}⟩ \\[4pt] −v &=⟨−3,−1⟩ \end{align*}\]
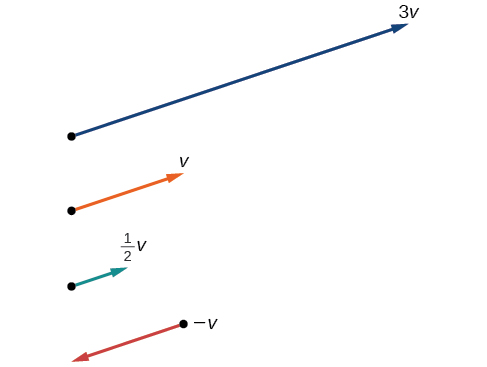
Figurine\(\PageIndex{12}\)
Analyse
Notez que le vecteur\(3\vec{v}\) mesure trois fois la longueur de\(\vec{v}\),\(\dfrac{1}{2}\vec{v}\) est la moitié de\(\vec{v}\) la longueur et\(\overrightarrow{–v}\) a la même longueur que\(\vec{v}\), mais dans la direction opposée.
Détermine le multiple scalaire\(3u\) donné\(\vec{u}=⟨5,4⟩\).
- Réponse
-
\(3u=⟨15,12⟩\)
Trouvez une équation linéaire à résoudre pour les quantités inconnues suivantes : Un nombre dépasse un autre nombre de\(17\) et leur somme est de\(31\). Trouve les deux numéros.
Solution
Tout d'abord, il faut multiplier chaque vecteur par le scalaire.
\[\begin{align*} 3u &= 3⟨3,−2⟩ \\[4pt] &= ⟨9,−6⟩ \\[4pt] 2v &= 2⟨−1,4⟩ \\[4pt] &= ⟨−2,8⟩ \end{align*}\]
Ajoutez ensuite les deux ensemble.
\[\begin{align*} w &= 3u+2v \\[4pt] &=⟨9,−6⟩+⟨−2,8⟩ \\[4pt] &= ⟨9−2,−6+8⟩ \\[4pt] &= ⟨7,2⟩ \end{align*}\]
Donc,\(w=⟨7,2⟩\).
Formulaire de recherche de composants
Dans certaines applications impliquant des vecteurs, il est utile de pouvoir décomposer un vecteur en ses composants. Les vecteurs sont composés de deux composantes : la composante horizontale est la\(x\) direction et la composante verticale est la\(y\) direction. Par exemple, nous pouvons voir sur le graphique de la figure\(\PageIndex{13}\) que le vecteur de position\(⟨2,3⟩\) provient de l'ajout des vecteurs\(v_1\) et\(v_2\). Nous avons\(v_2\) un point initial\((0,0)\) et un point terminal\((2,0)\).
\[\begin{align*} v_1 &= ⟨2−0,0−0⟩ \\[4pt] &= ⟨2,0⟩ \end{align*}\]
Nous avons également\(v_2\) un point initial\((0,0)\) et un point terminal\((0, 3)\).
\[\begin{align*} v_2 &= ⟨0−0,3−0⟩ \\[4pt] &= ⟨0,3⟩ \end{align*}\]
Par conséquent, le vecteur de position est
\[\begin{align*} v &= ⟨2+0,3+0⟩ \\[4pt] &= ⟨2,3⟩ \end{align*}\]
En utilisant le théorème de Pythagore, la magnitude de\(v_1\) est\(2\) et la magnitude de\(v_2\) est\(3\). Pour déterminer l'amplitude de\(v\), utilisez la formule avec le vecteur de position.
\[\begin{align*} |v| &= \sqrt{{|v_1|}^2+{|v_2|}^2} \\[4pt] &= \sqrt{2^2+3^2} \\[4pt] &= \sqrt{13} \end{align*}\]
L'ampleur de\(v\) est\(\sqrt{13}\). Pour trouver la direction, nous utilisons la fonction tangente\(\tan \theta=\dfrac{y}{x}\).
\[\begin{align*} \tan \theta &= \dfrac{v_2}{v_1} \\[4pt] \tan \theta &= \dfrac{3}{2} \\[4pt] \theta &={\tan}^{−1}\left(\dfrac{3}{2}\right)=56.3° \end{align*}\]
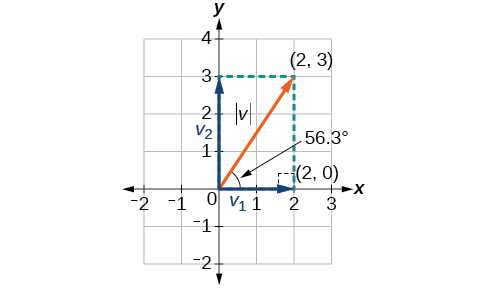
Figurine\(\PageIndex{13}\)
Ainsi, l'amplitude de\(\vec{v}\) est\(\sqrt{13}\) et la direction sont différentes\(56.3^{\circ}\) de l'horizontale.
Trouvez les composantes du vecteur \(\vec{v}\)avec le point initial\((3,2)\) et le point terminal\((7,4)\).
Solution
Trouvez d'abord la position standard.
\[\begin{align*} v &= ⟨7−3,4−2⟩ \\[4pt] &= ⟨4,2⟩ \end{align*}\]
Reportez-vous à l'illustration de la figure\(\PageIndex{14}\).
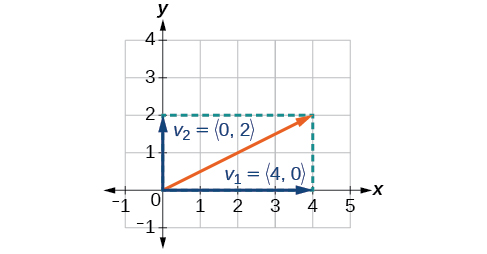
Figurine\(\PageIndex{14}\)
La composante horizontale est\(\vec{v_1}=⟨4,0⟩\) et la composante verticale est\(\vec{v_2}=⟨0,2⟩\).
Trouver le vecteur unitaire dans la direction de\(v\)
En plus de trouver les composants d'un vecteur, il est également utile pour résoudre des problèmes de trouver un vecteur dans la même direction que le vecteur donné, mais avec une amplitude\(1\). Nous appelons un vecteur dont l'amplitude\(1\) est un vecteur unitaire. Nous pouvons ensuite conserver la direction du vecteur d'origine tout en simplifiant les calculs.
Les vecteurs unitaires sont définis en termes de composants. Le vecteur unitaire horizontal s'écrit\(\vec{i}=⟨1,0⟩\) et est dirigé le long de l'axe horizontal positif. Le vecteur unitaire vertical s'écrit\(\vec{j}=⟨0,1⟩\) et est dirigé le long de l'axe vertical positif. Voir la figure\(\PageIndex{15}\).
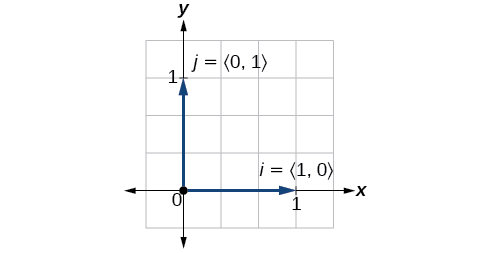
Figurine\(\PageIndex{15}\)
S'il s'\(\vec{v}\)agit d'un vecteur différent de zéro, il\(\dfrac{v}{| v |}\) s'agit d'un vecteur unitaire dans la direction de \(v\). Tout vecteur divisé par sa magnitude est un vecteur unitaire. Notez que la magnitude est toujours un scalaire, et diviser par un scalaire revient à multiplier par l'inverse du scalaire.
Trouvez un vecteur unitaire dans la même direction que\(v=⟨−5,12⟩\).
Solution
Tout d'abord, nous allons trouver l'ampleur.
\[\begin{align*} |v| &= \sqrt{{(−5)}^2+{(12)}^2} \\[4pt] &= \sqrt{25+144} \\[4pt] &=\sqrt{169} \\[4pt] &= 13 \end{align*}\]
Ensuite, nous divisons chaque composant par\(| v |\), ce qui donne un vecteur unitaire dans la même direction que\(\vec{v}\) :
\(\dfrac{v}{| v |} = −\dfrac{5}{13}i+\dfrac{12}{13}j \)
ou, sous forme de composant
\(\dfrac{v}{| v |}= \left \langle -\dfrac{5}{13},\dfrac{12}{13} \right \rangle\)
Voir la figure\(\PageIndex{16}\).
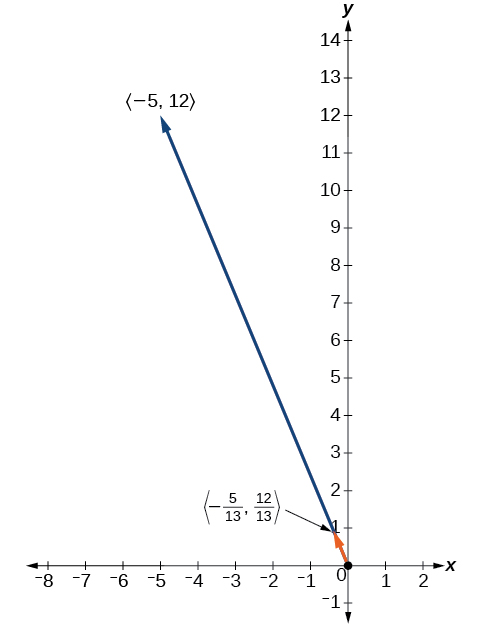
Figurine\(\PageIndex{16}\)
Vérifiez que l'amplitude du vecteur unitaire est égale\(1\). L'amplitude de\(−\dfrac{5}{13}i+\dfrac{12}{13}j\) est donnée sous la forme
\[\begin{align*} \sqrt{ {\left(−\dfrac{5}{13}\right)}^2+{ \left(\dfrac{12}{13}\right) }^2 } &= \sqrt{\dfrac{25}{169}+\dfrac{144}{169}} \\[4pt] &= \sqrt{\dfrac{169}{169}}\\ &=1 \end{align*}\]
Le vecteur\(u=\dfrac{5}{13}i+\dfrac{12}{13}j\) est le vecteur unitaire dans la même direction que\(v=⟨−5,12⟩\).
Réalisation d'opérations avec des vecteurs en termes de\(i\) et\(j\)
Jusqu'à présent, nous avons étudié les bases des vecteurs : magnitude et direction, addition et soustraction de vecteurs, multiplication scalaire, composantes des vecteurs et représentation géométrique des vecteurs. Maintenant que nous connaissons les stratégies générales utilisées pour travailler avec des vecteurs, nous allons représenter les vecteurs en coordonnées rectangulaires en termes de\(i\) et\(j\).
Étant donné qu'un vecteur\(\vec{v}\) avec le point initial\(P=(x_1,y_1)\) et le point\(Q=(x_2,y_2)\) terminal\(\vec{v}\) est écrit comme
\[v=(x_2−x_1)i+(y_1−y_2)j\]
Le vecteur de position de\((0,0)\) à\((a,b)\), où\((x_2−x_1)=a\) et\((y_2−y_1)=b\), s'écrit\(\vec{v} = \vec{ai}+ \vec{bj}\). Cette somme vectorielle est appelée combinaison linéaire des vecteurs\(\vec{i}\) et\(\vec{j}\).
L'amplitude de\(\vec{v} = \overrightarrow{ai} + \overrightarrow{bj}\) est donnée sous la forme\(| v |=\sqrt{a^2+b^2}\). Voir la figure\(\PageIndex{17}\).
.jpg)
Figurine\(\PageIndex{17}\)
Étant donné un vecteur\(\vec{v}\) avec un point initial\(P=(2,−6)\) et un point terminal\(Q=(−6,6)\), écrivez le vecteur en termes de\(\vec{i}\) et\(\vec{j}\).
Solution
Commencez par écrire la forme générale du vecteur. Remplacez ensuite les coordonnées par les valeurs données.
\[\begin{align*} v &= (x_2−x_1)i+(y_2−y_1)j \\[4pt] &=(−6−2)i+(6−(−6))j \\[4pt] &= −8i+12j \end{align*}\]
Étant donné le point initial\(P_1=(−1,3)\) et le point terminal\(P_2=(2,7)\), écrivez le vecteur\(\vec{v}\) en termes de\(\vec{i}\) et\(\vec{j}\).
Solution
Commencez par écrire la forme générale du vecteur. Remplacez ensuite les coordonnées par les valeurs données.
\[\begin{align*} v &= (x_2−x_1)i+(y_2−y_1)j \\[4pt] v &= (2−(−1))i+(7−3)j \\[4pt] &= 3i+4j \end{align*}\]
Écrivez le vecteur\(\vec{u}\) avec le point initial\(P=(−1,6)\) et le point terminal\(Q=(7,−5)\) en termes de\(\vec{i}\) et\(\vec{j}\).
- Réponse
-
\(u=8i−11j\)
Exécution d'opérations sur des vecteurs en termes de\(i\) et\(j\)
Lorsque les vecteurs sont écrits en termes de\(i\) et\(j\), nous pouvons effectuer des additions, des soustractions et des multiplications scalaires en effectuant des opérations sur les composants correspondants.
Donné\(v = ai + bj\) et\(u = ci + dj\), ensuite
\[\begin{align*} v+u &= (a+c)i+(b+d)j \\[4pt] v−u &= (a−c)i+(b−d)j \end{align*}\]
Trouvez la somme de\(v_1=2i−3j\) et\(v_2=4i+5j\).
Solution
\[\begin{align*} v_1+v_2 &= (2+4)i+(−3+5)j \\[4pt] &= 6i+2j \end{align*}\]
Calcul de la forme constitutive d'un vecteur : direction
Nous avons vu comment dessiner des vecteurs en fonction de leurs points initial et terminal et comment trouver le vecteur de position. Nous avons également examiné la notation des vecteurs dessinés spécifiquement dans le plan de coordonnées cartésien à l'aide de\(i\) et\(j\). Pour n'importe lequel de ces vecteurs, nous pouvons calculer la magnitude. Nous voulons maintenant combiner les points clés et examiner plus en détail les idées de magnitude et de direction.
Le calcul de la direction suit le même processus simple que celui utilisé pour les coordonnées polaires. Nous trouvons la direction du vecteur en déterminant l'angle par rapport à l'horizontale. Pour ce faire, nous utilisons les identités trigonométriques de base, mais\(| v |\) en les remplaçant\(r\).
Étant donné un vecteur de position\(v=⟨x,y⟩\) et un angle de direction\(\theta\),
\[ \begin{align*} \cos \theta &= \dfrac{x}{|v|} \text{ and } \sin \theta=y|v| \\[4pt] x &= |v| \cos \theta \\[4pt] y &= |v| \sin \theta \end{align*}\]
Ainsi\(v=xi+yj=| v | \cos \theta i+| v | \sin \theta j\), et l'amplitude est exprimée sous la forme\(| v |=\sqrt{x^2+y^2}\).
Écrivez un vecteur dont\(7\) la longueur fait un angle par rapport\(135°\) à l'axe X positif en termes de magnitude et de direction.
Solution
En utilisant les formules de conversion\(x=| v | \cos \theta i\) et\(y=| v | \sin \theta j\), nous constatons que
\[ \begin{align*} x &= 7\cos(135°)i \\[4pt] &= −\dfrac{7\sqrt{2}}{2} \\[4pt] y &=7 \sin(135°)j \\[4pt] &= \dfrac{7\sqrt{2}}{2} \end{align*}\]
Ce vecteur peut être écrit\(v=7\cos(135°)i+7\sin(135°)j\) ou simplifié en tant que
\(v=−\dfrac{7\sqrt{2}}{2}i+\dfrac{7\sqrt{2}}{2}j\)
Un vecteur se déplace de l'origine au point\((3,5)\). Écrivez le vecteur en termes de magnitude et de direction.
- Réponse
-
\(v=\sqrt{34}\cos(59°)i+\sqrt{34}\sin(59°)j\)
Magnitude =\(34\)
\(\theta={\tan}^{−1}\left(\dfrac{5}{3}\right)=59.04°\)
Trouver le produit scalaire de deux vecteurs
Comme nous l'avons vu plus haut dans la section, la multiplication scalaire consiste à multiplier un vecteur par un scalaire, et le résultat est un vecteur. Comme nous l'avons vu, la multiplication d'un vecteur par un nombre est appelée multiplication scalaire. Si nous multiplions un vecteur par un vecteur, il existe deux possibilités : le produit scalaire et le produit croisé. Nous examinerons uniquement le produit scalaire ici ; vous pouvez rencontrer le produit croisé dans des cours de mathématiques plus avancés.
Le produit scalaire de deux vecteurs implique la multiplication de deux vecteurs ensemble, et le résultat est un scalaire.
Le produit scalaire de deux vecteurs\(v=⟨a,b⟩\)\(u=⟨c,d⟩\) est la somme du produit des composantes horizontales et du produit des composantes verticales.
\[v⋅u=ac+bd\]
Pour déterminer l'angle entre les deux vecteurs, utilisez la formule ci-dessous.
\[\cos \theta=\dfrac{v}{| v |}⋅\dfrac{u}{| u |}\]
Trouvez le produit scalaire de\(v=⟨5,12⟩\) et\(u=⟨−3,4⟩\).
Solution
En utilisant la formule, nous avons
\[\begin{align*} v⋅u &= ⟨5,12⟩⋅⟨−3,4⟩ \\[4pt] &= 5⋅(−3)+12⋅4 \\[4pt] &= −15+48 \\[4pt] &= 33 \end{align*}\]
Trouvez le produit scalaire de\(v_1 = 5i + 2j\) et\(v_2 = 3i + 7j\). Ensuite, trouvez l'angle entre les deux vecteurs.
Solution
En trouvant le produit scalaire, nous multiplions les composants correspondants.
\[ \begin{align*} v_1⋅v_2 &= ⟨5,2⟩⋅⟨3,7⟩ \\[4pt] &= 5⋅3+2⋅7 \\[4pt] &= 15+14 \\[4pt] &= 29 \end{align*}\]
Pour trouver l'angle entre eux, nous utilisons la formule\(\cos \theta=\dfrac{v}{|v|}⋅\dfrac{u}{|u|}\).
\[\begin{align*} \dfrac{v}{|v|}\cdot \dfrac{u}{|u|} &= \left \langle \dfrac{5}{\sqrt{29}}+\dfrac{2}{\sqrt{29}} \right \rangle \cdot \left \langle \dfrac{3}{\sqrt{58}}+\dfrac{7}{\sqrt{58}} \right \rangle \\[4pt] &=\dfrac{5}{\sqrt{29}}\cdot \dfrac{3}{\sqrt{58}}+\dfrac{2}{\sqrt{29}}\cdot \dfrac{7}{\sqrt{58}} \\[4pt] &= \dfrac{15}{\sqrt{1682}}+\dfrac{14}{\sqrt{1682}}\\ &=\dfrac{29}{\sqrt{1682}} \\[4pt] &= 0.707107 \\[4pt] {\cos}^{-1}(0.707107) &= 45° \end{align*}\]
Voir la figure\(\PageIndex{18}\).
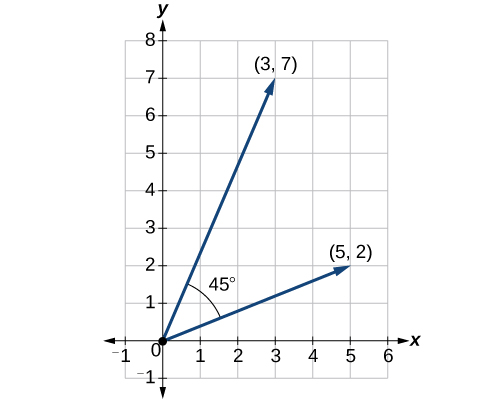
Figurine\(\PageIndex{18}\)
Trouvez l'angle entre\(u=⟨−3,4⟩\) et\(v=⟨5,12⟩\).
Solution
En utilisant la formule, nous avons
\[\begin{align*} \theta &= {\cos}^{−1}\left(\dfrac{u}{|u|}⋅\dfrac{v}{|v|}\right) \\[4pt] \left(\dfrac{u}{|u|}⋅\dfrac{v}{|v|}\right) &= \dfrac{−3i+4j}{5}⋅\dfrac{5i+12j}{13} \\[4pt] &= \left(− \dfrac{3}{5}⋅ \dfrac{5}{13}\right)+\left(\dfrac{4}{5}⋅ \dfrac{12}{13}\right) \\[4pt] &= −\dfrac{15}{65}+\dfrac{48}{65} \\[4pt] &= \dfrac{33}{65} \\[4pt] \theta &= {\cos}^{−1}\left(\dfrac{33}{65}\right) \\[4pt] &= 59.5^{\circ} \end{align*}\]
Voir la figure\(\PageIndex{19}\).
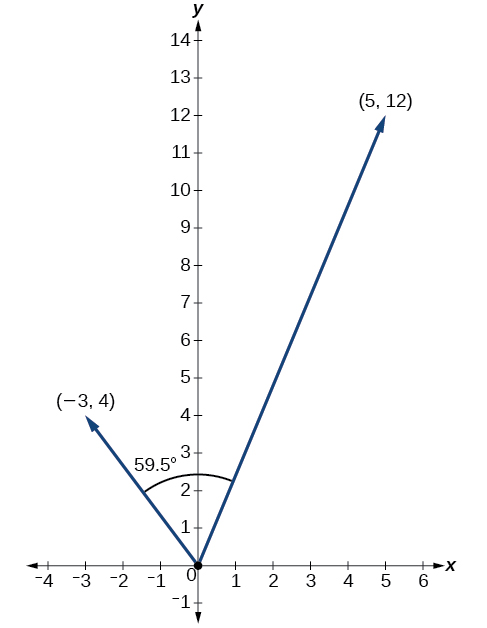
Figurine\(\PageIndex{19}\)
Nous avons maintenant les outils pour résoudre le problème que nous avons introduit en ouverture de la section.
Un avion vole à une vitesse anémométrique de\(200\) miles par heure en direction d'un cap SE de\(140°\). Un vent du nord (du nord au sud) souffle à des\(16.2\) milles à l'heure. Quelles sont la vitesse au sol et l'orientation réelle de l'avion ? Voir la figure\(\PageIndex{20}\).
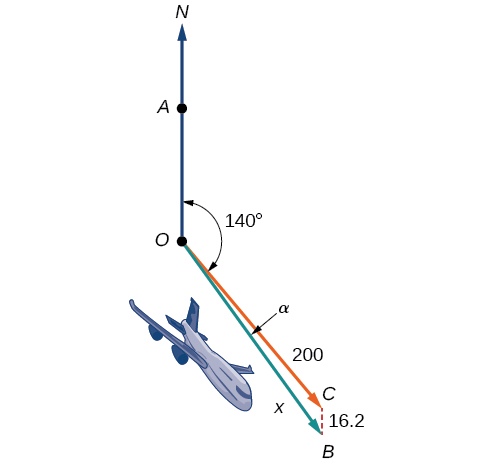
Figurine\(\PageIndex{20}\)
Solution
La vitesse du sol est\(x\) représentée par le diagramme, et nous devons trouver l'angle\(\alpha\) afin de calculer le roulement ajusté, qui sera le cas\(140°+\alpha\).
Remarquez sur la figure\(\PageIndex{20}\) que cet angle\(\angle BCO\) doit être égal à l'angle\(\angle AOC\) selon la règle de l'alternance des angles intérieurs, donc l'angle\(\angle BCO\) est de 140°. On peut trouver\(x\) par la loi des cosinus :
\[\begin{align*} x^2 &= {(16.2)}^2+{(200)}^2−2(16.2)(200) \cos(140°) \\[4pt] x^2 &= 45,226.41 \\[4pt] x &= \sqrt{45,226.41} \\[4pt] x &= 212.7 \end{align*}\]
La vitesse au sol est d'environ\(213\) miles par heure. Nous pouvons maintenant calculer le relèvement en utilisant la loi des sinus.
\[\begin{align*} \dfrac{\sin \alpha}{16.2} &= \dfrac{\sin(140°)}{212.7} \\[4pt] \sin \alpha &= \dfrac{16.2 \sin(140°)}{212.7} \\[4pt] &=0.04896 \\[4pt] {\sin}^{−1}(0.04896) &= 2.8° \end{align*}\]
Par conséquent, l'avion a un palier SE de\(140°+2.8°=142.8°\). La vitesse au sol est\(212.7\) de miles par heure.
Key Concepts
- The position vector has its initial point at the origin. See Example \(\PageIndex{1}\).
- If the position vector is the same for two vectors, they are equal. See Example \(\PageIndex{2}\).
- Vectors are defined by their magnitude and direction. See Example \(\PageIndex{3}\).
- If two vectors have the same magnitude and direction, they are equal. See Example \(\PageIndex{4}\).
- Vector addition and subtraction result in a new vector found by adding or subtracting corresponding elements. See Example \(\PageIndex{5}\).
- Scalar multiplication is multiplying a vector by a constant. Only the magnitude changes; the direction stays the same. See Example \(\PageIndex{6}\) and Example \(\PageIndex{7}\).
- Vectors are comprised of two components: the horizontal component along the positive \(x\)-axis, and the vertical component along the positive \(y\)-axis. See Example \(\PageIndex{8}\).
- The unit vector in the same direction of any nonzero vector is found by dividing the vector by its magnitude.
- The magnitude of a vector in the rectangular coordinate system is \(| v |=\sqrt{a^2+b^2}\). See Example \(\PageIndex{9}\).
- In the rectangular coordinate system, unit vectors may be represented in terms of \(ii\) and \(jj\) where \(i\) represents the horizontal component and \(j\) represents the vertical component. Then, \(v = ai + bj\) is a scalar multiple of \(v\) by real numbers \(a\) and \(b\). See Example \(\PageIndex{10}\) and Example \(\PageIndex{11}\).
- Adding and subtracting vectors in terms of \(i\) and \(j\) consists of adding or subtracting corresponding coefficients of \(i\) and corresponding coefficients of \(j\). See Example \(\PageIndex{12}\).
- A vector \(v = ai + bj\) is written in terms of magnitude and direction as \(v=| v |\cos \theta i+| v |\sin \theta j\). See Example \(\PageIndex{13}\).
- The dot product of two vectors is the product of the \(i\) terms plus the product of the \(j\) terms. See Example \(\PageIndex{14}\).
- We can use the dot product to find the angle between two vectors. Example \(\PageIndex{15}\) and Example \(\PageIndex{16}\).
- Dot products are useful for many types of physics applications. See Example \(\PageIndex{17}\).


