10.7 : Équations paramétriques - Graphiques
- Page ID
- 195526
- Tracez des courbes planes décrites par des équations paramétriques en traçant des points.
- Tracez des équations paramétriques
C'est la fin de la neuvième manche, avec deux retraits et deux hommes sur les buts. L'équipe locale perd de deux points. Le frappeur se balance et frappe la balle à\(140\) pieds par seconde et à un angle d'environ par rapport\(45°\) à l'horizontale. Jusqu'où se déplacera le ballon ? Cela ouvrira-t-il la clôture pour un home run gagnant ? Le résultat peut dépendre en partie d'autres facteurs (par exemple, le vent), mais les mathématiciens peuvent modéliser la trajectoire d'un projectile et prédire approximativement la distance qu'il parcourra à l'aide d'équations paramétriques. Dans cette section, nous aborderons les équations paramétriques et certaines applications courantes, telles que les problèmes de mouvement des projectiles.

Figure\(\PageIndex{1}\) : Les équations paramétriques peuvent modéliser la trajectoire d'un projectile. (crédit : Paul Kreher, Flickr)
Représentation graphique d'équations paramétriques en traçant des points
Au lieu d'utiliser une calculatrice graphique ou un programme informatique de création de graphiques, la méthode standard consiste à tracer des points pour représenter le graphe d'une équation. Tant que nous calculons les valeurs avec soin, le tracé par points est très fiable.
- Construisez un tableau à trois colonnes :\(t\),\(x(t)\), et\(y(t)\).
- Evaluez\(x\) et\(y\) pour les valeurs de tt sur l'intervalle pour lequel les fonctions sont définies.
- Tracez les paires résultantes\((x,y)\).
Esquissez le graphe des équations paramétriques\(x(t)=t^2+1\),\( y(t)=2+t\).
Solution
Construisez un tableau de valeurs pour\(t\)\(x(t)\), et\(y(t)\), comme dans Tableau\(\PageIndex{1}\), et tracez les points dans un plan.
| \(t\) | \(x(t)=t^2+1\) | \(y(t)=2+t\) |
|---|---|---|
| \(−5\) | \(26\) | \(−3\) |
| \(−4\) | \(17\) | \(−2\) |
| \(−3\) | \(10\) | \(−1\) |
| \(−2\) | \(5\) | \(0\) |
| \(−1\) | \(2\) | \(1\) |
| \(0\) | \(1\) | \(2\) |
| \(1\) | \(2\) | \(3\) |
| \(2\) | \(5\) | \(4\) |
| \(3\) | \(10\) | \(5\) |
| \(4\) | \(17\) | \(6\) |
| \(5\) | \(26\) | \(7\) |
Le graphique est une parabole dont le sommet\((1,2)\) s'ouvre vers la droite. Voir la figure\(\PageIndex{2}\).
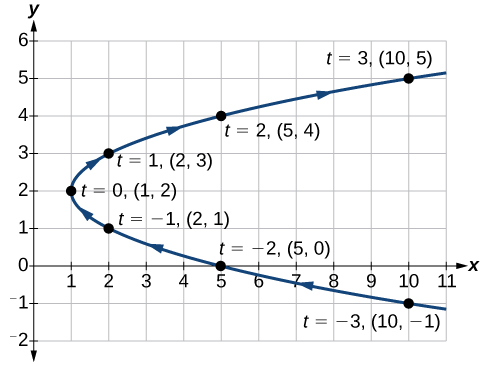
Figurine\(\PageIndex{2}\)
Analyse
En tant que valeurs de\(t\) progression dans une direction positive de\(0\) à\(5\), les points tracés tracent la moitié supérieure de la parabole. Lorsque les valeurs deviennent généralement négatives, elles tracent la moitié inférieure de la parabole. Il n'y a aucune restriction sur le domaine. Les flèches indiquent la direction en fonction des valeurs croissantes de\(t\). Le graphique ne représente pas une fonction, car il échouera au test de la ligne verticale. Le graphique est dessiné en deux parties : les valeurs positives pour\(t\) et les valeurs négatives pour\(t\).
Esquissez le graphe des équations paramétriques\(x=\sqrt{t}\),\( y=2t+3\),\(0≤t≤3\).
- Réponse
-
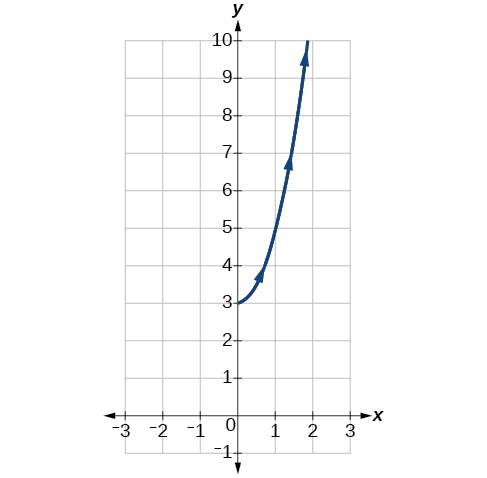
Figurine\(\PageIndex{3}\)
Construisez un tableau de valeurs pour les équations paramétriques données et esquissez le graphique :
\(x=2 \cos t\)
\(y=4 \sin t\)
Solution
Construisez une table comme celle dans Table en\(\PageIndex{2}\) utilisant la mesure de l'angle en radians comme entrées pour\(t\), et en évaluant\(x\) et\(y\). L'utilisation d'angles dont les valeurs de sinus et de cosinus sont connues\(t\) facilite les calculs.
| \(t\) | \(x=2 \cos t\) | \(y=4 \sin t\) |
|---|---|---|
| \(0\) | \(x=2 \cos(0)=2\) | \(y=4 \sin(0)=0\) |
| \(\dfrac{\pi}{6}\) | \(x=2 \cos(\dfrac{\pi}{6})=\sqrt{3}\) | \(y=4 \sin(\dfrac{π}{6})=2\) |
| \(\dfrac{\pi}{3}\) | \(x=2 \cos(\dfrac{\pi}{3})=1\) | \(y=4 \sin(\dfrac{\pi}{3})=2\sqrt{3}\) |
| \(\dfrac{\pi}{2}\) | \(x=2 \cos(\dfrac{\pi}{2})=0\) | \(y=4 \sin(\dfrac{\pi}{2})=4\) |
| \(\dfrac{2\pi}{3}\) | \(x=2 \cos(\dfrac{2\pi}{3})=−1\) | \(y=4 \sin(\dfrac{2\pi}{3})=2\sqrt{3}\) |
| \(\dfrac{5\pi}{6}\) | \(x=2 \cos(\dfrac{5\pi}{6})=−\sqrt{3}\) | \(y=4 \sin(\dfrac{5\pi}{6})=2\) |
| \(\pi\) | \(x=2 \cos(\pi)=−2\) | \(y=4 \sin(\pi)=0\) |
| \(\dfrac{7\pi}{6}\) | \(x=2 \cos(\dfrac{7\pi}{6})=−\sqrt{3}\) | \(y=4 \sin(\dfrac{7\pi}{6})=−2\) |
| \(\dfrac{4\pi}{3}\) | \(x=2 \cos(\dfrac{4\pi}{3})=−1\) | \(y=4 \sin(\dfrac{4\pi}{3})=−2\sqrt{3}\) |
| \(\dfrac{3\pi}{2}\) | \(x=2 \cos(\dfrac{3\pi}{2})=0\) | \(y=4 \sin(\dfrac{3\pi}{2})=−4\) |
| \(\dfrac{5\pi}{3}\) | \(x=2 \cos(\dfrac{5\pi}{3})=1\) | \(y=4 \sin(\dfrac{5\pi}{3})=−2\sqrt{3}\) |
| \(\dfrac{11\pi}{6}\) | \(x=2 \cos(\dfrac{11\pi}{6})=\sqrt{3}\) | \(y=4 \sin(\dfrac{11\pi}{6})=−2\) |
| \(2\pi\) | \(x=2 \cos(2\pi)=2\) | \(y=4 \sin(2\pi)=0\) |
La figure\(\PageIndex{4}\) montre le graphique.
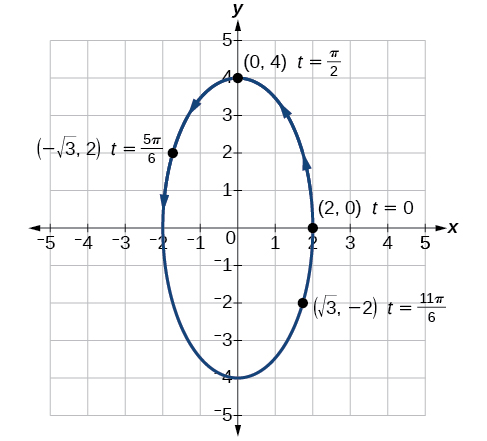
Figurine\(\PageIndex{4}\)
Par la symétrie indiquée dans les valeurs de\(x\) et\(y\), nous voyons que les équations paramétriques représentent une ellipse. L'ellipse est cartographiée dans le sens antihoraire, comme le montrent les flèches indiquant\(t\) des valeurs croissantes.
Analyse
Nous avons vu que les équations paramétriques peuvent être représentées graphiquement en traçant des points. Cependant, une calculatrice graphique permet de gagner du temps et de révéler les nuances d'un graphique qui peuvent être trop fastidieuses à découvrir en utilisant uniquement des calculs manuels. Assurez-vous de changer le mode de la calculatrice en mode paramétrique (PAR). Pour confirmer, la\(Y=\) fenêtre doit s'afficher
\[\begin{align*} X_{1T} &= \\ Y_{1T} &= \end{align*}\]
au lieu de\(Y_1=\).
Représentez graphiquement les équations paramétriques :\(x=5 \cos t\),\(y=3 \sin t\).
- Réponse
-
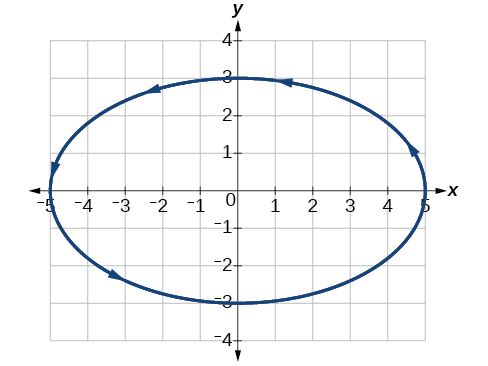
Figurine\(\PageIndex{5}\)
Tracez les équations paramétriques\(x=5 \cos t\) et\(y=2 \sin t\). Commencez par construire le graphique à l'aide des points de données générés à partir du formulaire paramétrique. Tracez ensuite la forme rectangulaire de l'équation. Comparez les deux graphiques.
Solution
Construisez un tableau de valeurs similaire à celui de Tableau\(\PageIndex{3}\).
| \(t\) | \(x=5 \cos t\) | \(y=2 \sin t\) |
|---|---|---|
| \(0\) | \(x=5 \cos(0)=5\) | \(y=2 \sin(0)=0\) |
| \(1\) | \(x=5 \cos(1)≈2.7\) | \(y=2 \sin(1)≈1.7\) |
| \(2\) | \(x=5 \cos(2)≈−2.1\) | \(y=2 \sin(2)≈1.8\) |
| \(3\) | \(x=5 \cos(3)≈−4.95\) | \(y=2 \sin(3)≈0.28\) |
| \(4\) | \(x=5 \cos(4)≈−3.3\) | \(y=2 \sin(4)≈−1.5\) |
| \(5\) | \(x=5 \cos(5)≈1.4\) | \(y=2 \sin(5)≈−1.9\) |
| \(−1\) | \(x=5 \cos(−1)≈2.7\) | \(y=2 \sin(−1)≈−1.7\) |
| \(−2\) | \(x=5 \cos(−2)≈−2.1\) | \(y=2 \sin(−2)≈−1.8\) |
| \(−3\) | \(x=5 \cos(−3)≈−4.95\) | \(y=2 \sin(−3)≈−0.28\) |
| \(−4\) | \(x=5 \cos(−4)≈−3.3\) | \(y=2 \sin(−4)≈1.5\) |
| \(−5\) | \(x=5 \cos(−5)≈1.4\) | \(y=2 \sin(−5)≈1.9\) |
\((x,y)\)Tracez les valeurs du tableau (Figure\(\PageIndex{6}\)).
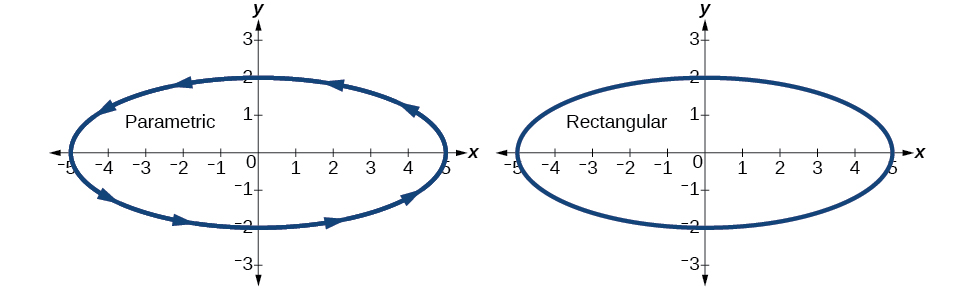
Figurine\(\PageIndex{6}\)
Ensuite, traduisez les équations paramétriques en forme rectangulaire. Pour ce faire, nous résolvons\(t\) dans l'un\(x(t)\) ou l'autre\(y(t)\), puis nous substituons l'expression par\(t\) dans l'autre équation. Le résultat sera une fonction\(y(x)\) si vous résolvez pour\(t\) en fonction de\(x\), ou\(x(y)\) si vous résolvez pour\(t\) en fonction de\(y\).
\[\begin{align*} x &= 5 \cos t \\ \dfrac{x}{5} &= \cos t \end{align*}\]
Résolvez pour\(\cos t\).
\(y=2 \sin t\)
Résolvez pour\(\sin t\).
\(\dfrac{y}{2}=\sin t\)
Ensuite, utilisez le théorème de Pythagore.
\[\begin{align*} {\cos}^2 t+{\sin}^2 t &=1 \\ {\left(\dfrac{x}{5}\right)}^2+{\left(\dfrac{y}{2}\right)}^2 &= 1 \\ \dfrac{x^2}{25}+\dfrac{y^2}{4} &=1 \end{align*}\]
Analyse
Dans la figure\(\PageIndex{7}\), les données des équations paramétriques et de l'équation rectangulaire sont tracées ensemble. Les équations paramétriques sont tracées en bleu ; le graphique de l'équation rectangulaire est dessiné au-dessus de l'équation paramétrique dans un style pointillé coloré en rouge. Il est clair que les deux formulaires produisent le même graphique.
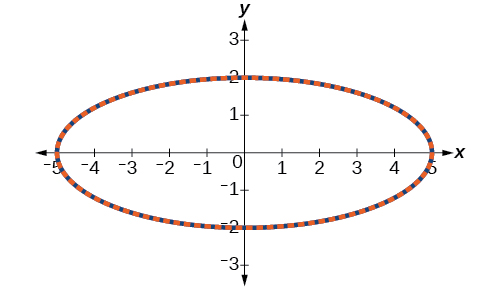
Figurine\(\PageIndex{7}\)
Représentez graphiquement les équations paramétriques\(x=t+1\) et\(y=\sqrt{t}\)\(t≥0\), et l'équivalent rectangulaire\(y=\sqrt{x−1}\) sur le même système de coordonnées.
Solution
Construisez un tableau de valeurs pour les équations paramétriques, comme nous l'avons fait dans l'exemple précédent, et tracez un graphique\(y=\sqrt{t}\)\(t≥0\) sur la même grille, comme dans la figure\(\PageIndex{8}\).
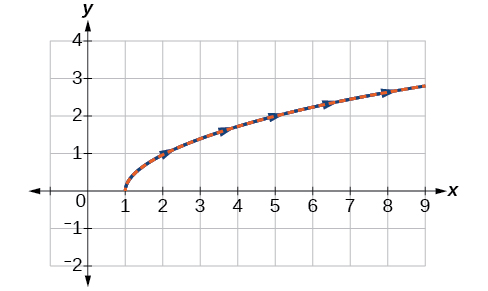
Figurine\(\PageIndex{8}\)
Analyse
Lorsque le domaine est\(t\) restreint, nous ne traçons que les valeurs positives de\(t\). Les données paramétriques sont représentées en bleu et le graphique de l'équation rectangulaire est pointillé en rouge. Une fois de plus, on constate que les deux formes se chevauchent.
Esquissez le graphique des équations paramétriques\(x=2 \cos \theta\) et\(y=4 \sin \theta\), avec l'équation rectangulaire, sur la même grille.
- Réponse
-
Le graphique des équations paramétriques est en rouge et le graphique de l'équation rectangulaire est dessiné en points bleus au-dessus des équations paramétriques.
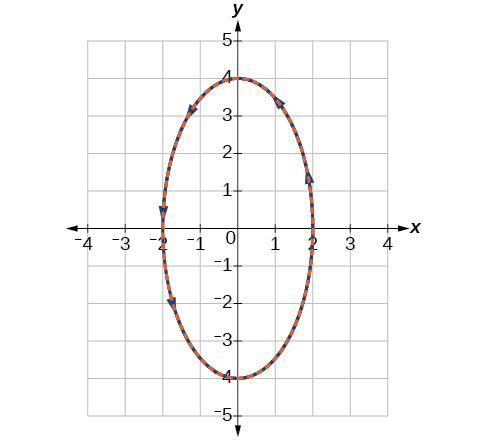
Figurine\(\PageIndex{9}\)
Applications des équations paramétriques
De nombreux avantages des équations paramétriques deviennent évidents lorsqu'elles sont appliquées à la résolution de problèmes du monde réel. Bien que les équations rectangulaires contenues dans\(x\) et\(y\) donnent une image globale de la trajectoire d'un objet, elles ne révèlent pas la position de l'objet à un moment précis. Les équations paramétriques illustrent toutefois la façon dont les valeurs\(x\) et\(y\) changent en fonction de la position d'un objet en mouvement à un moment donné\(t\), par exemple.
Une application courante des équations paramétriques consiste à résoudre des problèmes liés au mouvement des projectiles. Dans ce type de mouvement, un objet est propulsé vers l'avant dans une direction ascendante formant un angle par rapport\(\theta\) à l'horizontale, à une vitesse initiale et à une hauteur\(h\) au-dessus de\(v_0\) l'horizontale.
La trajectoire d'un objet propulsé avec une inclinaison par rapport\(\theta\) à l'horizontale, à une vitesse\(v_0\) initiale et à une hauteur\(h\) au-dessus de l'horizontale, est donnée par
\[\begin{align*} x &= (v_0 \cos \theta)t \\ y &= −\dfrac{1}{2}gt^2+(v_0 \sin \theta)t+h \end{align*}\]
où\(g\) tient compte des effets de la gravité et\(h\) est la hauteur initiale de l'objet. Selon les unités impliquées dans le problème, utilisez\(g=32 ft / s^2\) ou\(g=9.8 m / s^2\). L'équation pour\(x\) donne la distance horizontale et l'équation pour\(y\) donne la distance verticale.
- La distance horizontale est donnée par\(x=(v_0 \cos \theta)t\). Remplacez la vitesse initiale de l'objet par\(v_0\).
- L'expression\(\cos \theta\) indique l'angle selon lequel l'objet est propulsé. Remplacez cet angle en degrés par\(\cos \theta\).
- La distance verticale est donnée par la formule\(y=−\dfrac{1}{2}gt^2+(v_0 \sin \theta)t+h\). Le terme\(−\dfrac{1}{2}gt^2\) représente l'effet de la gravité. Selon les unités impliquées, utilisez\(g=32 ft/s^2\) ou\(g=9.8 m/s^2\). Encore une fois, remplacez la vitesse initiale par et la hauteur à laquelle l'objet a été propulsé\(h\).\(v_0\)
- Procédez en calculant chaque terme à résoudre\(t\).
Résolvez le problème présenté au début de cette section. Est-ce que le frappeur réussit le home run gagnant ? Supposons que la balle soit frappée à une vitesse initiale de\(140\) pieds par seconde à un angle égal\(45°\) à l'horizontale, en entrant en contact\(3\) pieds au-dessus du sol.
- Trouvez les équations paramétriques pour modéliser la trajectoire de la balle de baseball.
- Où est le ballon après\(2\) quelques secondes ?
- Combien de temps dure la balle en l'air ?
- Est-ce un home run ?
Solution
1. Utilisez les formules pour configurer les équations. La position horizontale est déterminée à l'aide de l'équation paramétrique pour\(x\). Ainsi,
\[\begin{align*} x &= (v_0 \cos \theta)t \\ x &= (140 \cos(45°))t \end{align*}\]
La position verticale est déterminée à l'aide de l'équation paramétrique pour\(y\). Ainsi,
\[\begin{align*} y &=−16t^2+(v_0 \sin \theta)t+h \\ y &= −16t^2+(140 \sin(45°))t+3 \end{align*}\]
2. \(2\)Remplacez les équations pour trouver les positions horizontale et verticale de la balle.
\[\begin{align*} x &= (140 \cos(45°))(2) \\ x &= 198\space feet \\ y &= −16{(2)}^2+(140 \sin(45°))(2)+3 \\ y &=137\space feet \end{align*}\]
Après\(2\) quelques secondes, le ballon est à quelques\(198\) pieds de la surface du frappeur et les\(137\) pieds au-dessus du sol.
3. Pour calculer combien de temps la balle reste en l'air, nous devons savoir quand elle va toucher le sol ou quand\(y=0\). Ainsi,
\[\begin{align*} y &= −16t^2+(140\sin(45∘))t+3 \\ y &=0 \text{ Set }y(t)=0 \text{ and solve the quadratic.} \\ t &= 6.2173 \end{align*}\]
En\(t=6.2173\) quelques secondes, la balle a touché le sol. (L'équation quadratique peut être résolue de différentes manières, mais ce problème a été résolu à l'aide d'un programme informatique de mathématiques.)
4. Nous ne pouvons pas confirmer qu'il s'agissait d'un home run sans tenir compte de la taille du champ extérieur, qui varie d'un terrain à l'autre. Cependant, par souci de simplicité, supposons que le mur extérieur se trouve à quelques pas de\(400\) la plaque d'attache, dans la partie la plus profonde du parc. Supposons également que le mur mesure quelques\(10\) pieds de haut. Afin de déterminer si la balle franchit le mur, nous devons calculer la hauteur de la balle lorsque vous êtes\(x = 400\) pieds. Nous allons donc définir\(x = 400\), résoudre et saisir tt dans\(y\).\(t\)
\[\begin{align*} x &= (140 \cos(45°))t \\ 400 &= (140 \cos(45°))t \\ t &= 4.04 \\ y &= −16{(4.04)}^2+(140 \sin(45°))(4.04)+3 \\ y &= 141.8 \end{align*}\]
La balle est les\(141.8\) pieds en l'air lorsqu'elle sort du terrain de jeu. C'était en effet un home run. Voir la figure\(\PageIndex{10}\).

Figurine\(\PageIndex{10}\)
Accédez à la ressource en ligne suivante pour obtenir des instructions et des exercices supplémentaires sur les graphes d'équations paramétriques.
Key Concepts
- When there is a third variable, a third parameter on which \(x\) and \(y\) depend, parametric equations can be used.
- To graph parametric equations by plotting points, make a table with three columns labeled \(t\), \(x(t)\), and \(y(t)\). Choose values fort t in increasing order. Plot the last two columns for \(x\) and \(y\). See Example \(\PageIndex{1}\) and Example \(\PageIndex{2}\).
- When graphing a parametric curve by plotting points, note the associated t-values and show arrows on the graph indicating the orientation of the curve. See Example \(\PageIndex{3}\) and Example \(\PageIndex{4}\).
- Parametric equations allow the direction or the orientation of the curve to be shown on the graph. Equations that are not functions can be graphed and used in many applications involving motion. See Example \(\PageIndex{5}\).
- Projectile motion depends on two parametric equations: \(x=(v_0 \cos \theta)t\) and \(y=−16t^2+(v_0 \sin \theta)t+h\). Initial velocity is symbolized as \(v_0\). \(\theta\) represents the initial angle of the object when thrown, and \(h\) represents the height at which the object is propelled.


